文章信息
- 胡长江, 李英冰
- HU Changjiang, LI Yingbing
- GNSS-R星载测高的动态性误差和信号平行误差研究
- Dynamic Error and Parallel Signal Error in GNSS-R Spaceborne Altimetry
- 武汉大学学报·信息科学版, 2015, 40(12): 1695-1700
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1695-1700
- http://dx.doi.org/10.13203/j.whugis20130819
-
文章历史
- 收稿日期: 2014-10-09

自1993年Martin-Neira提出PARIS(Passive Reflectometry and Interferometry System)概念以来[1],国内外已有很多学者对这一新型技术进行了理论和实验研究[2, 3]。在星载几何模型问题上,Martin-Neira在提出PARIS概念时就研究了路径延迟误差和垂线偏差对测高的影响[1];2003年,Wagner等从误差传播的理论出发,分析了接收机与发射机的径向误差、接收机与发射机的地心夹角误差以及路径延迟误差对测高的影响[4]。2005年,Kostelecky等分析了星载情况下接收机与发射机的轨道误差对镜面反射点垂直方向上分量的影响[5],得出了在需要获得dm级或更高精度的情况下,测高结果需要考虑轨道误差的结论。2012年,Valencia等分析星载模式与机载和岸基模式在接收机平台高度和动态性方面的不同[6],但主要分析内容是这些因素对反演海表状态的影响。
目前对几何模型的研究主要集中在利用不同的方法分析不同因素(如轨道误差和路径延迟误差)对测高的影响,但涉及星载模式下发射机的动态性误差以及假设信号平行传播对测高的影响的研究相对较少。另外,星载模式相对其他模式具有如下优点: (1) 通过精密定轨可以得到高精度的接收机和发射机的位置信息;(2) 能够进行大范围的测高;(3) 重返周期短[7];(4) 反射事件密度大[4, 7]。这些优点使星载模式正成为未来GNSS-R测高的发展趋势。基于此,本文基于目前GNSS-R星载测高的几何路径延迟模型,分析了该模型中存在的动态性误差和信号平行误差。
1 动态性误差分析GNSS-R测高利用直射信号与反射信号之间的路径延迟来反演接收机平台相对给定参考面的高度。在提取延迟时,GNSS-R接收机获取的是某一时刻到达接收机的直射信号与反射信号的群延迟之差。由于直射信号与反射信号是卫星在不同时刻发出的,因此经历了不同的传播时间后,能够被同时接收。而目前的几何模型中普遍没有考虑这一因素的影响。
图1是动态性误差的示意图。图1中R表示接收机,发射机在T处( t1时刻)发射的信号经反射后到达接收机,在T′处(t2时刻)发射的信号直接被接收机接收,S是镜面反射点。提取的时间延迟为:

式(1)两边同时乘以光速得到路径延迟:

没有考虑发射机动态性时的路径延迟为:
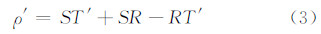
所以由式(2)~(3)得到由动态性引起的路径延迟误差:
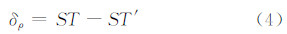
而路径延迟误差δρ与测高(海面相对椭球面的高)误差δH之间的关系为[1, 4]:

式中,θ为镜面反射点处的卫星高度角。结合式(4)、式(5)可得发射机的动态性引起的测高误差为:
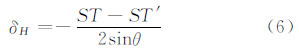

|
| 图 1 动态性误差示意图 Fig. 1 Illustration of Dynamic Error |
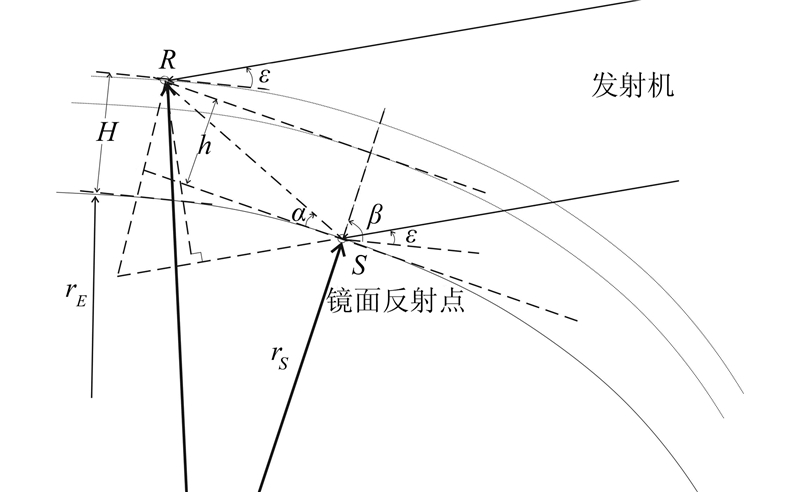
图2是GNSS-R星载测高的一种几何模型[8],图2中 R表示接收机,S表示镜面反射点,rE表示接收机星下点的平均曲率半径,rS表示镜面反射点到地心的距离,α表示镜面反射点处的接收机高度角,β表示镜面反射点的方向角,ε表示接收机处的卫星高度角,H表示接收机相对参考面的高,h表示接收机到镜面反射点处切平面的距离。H可以由式(7)求得[8]:
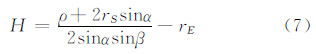
海面相对椭球面的高h1可由接收机相对椭球面的高Hm减去接收机相对海面的高Ho得到,即:

式中,σion表示电离层引起的测高误差;σtro表示对流层引起的测高误差;n表示噪声。用式(7)计算Hm时,式(7)中的参数均用椭球模型(如WGS84椭球)求得。计算Ho时,路径延迟ρo是观测值,rSo、αo、βo和rEo通过模型求得。用图2的模型进行海面测高时存在动态性误差,即使假设信号平行传播,也会对测高产生误差。
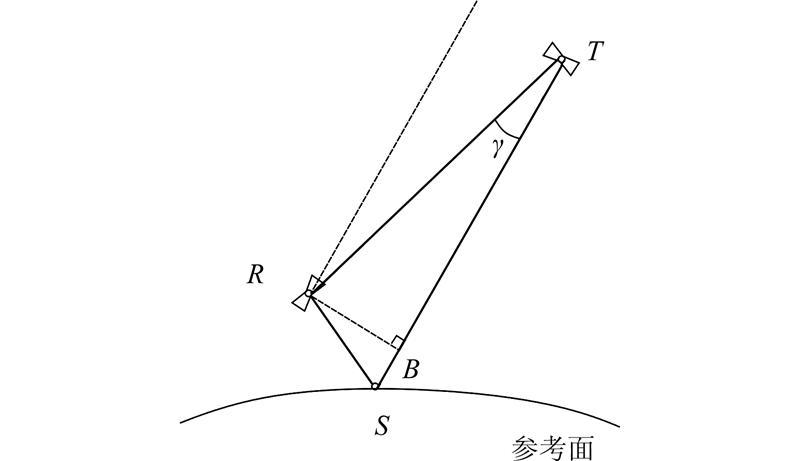
图3描述了假设信号平行传播对路径延迟的影响,在这一假设下,路径延迟:
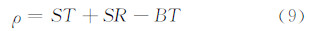
|
| 图 3 信号平行误差示意图 Fig. 3 Illustration of Parallel Signal Error |
而实际的路径延迟ρ′为:

式(10)减式(9)得到由此引起的路径延迟误差:
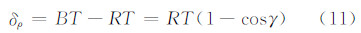
式中,γ为卫星到接收机的向量 TR 与卫星到镜面反射点的向量 TS 的夹角。式(8)两边同时对ρ求偏导可以得到该模型下路径延迟误差与测高(海面相对椭球面的高)误差之间的关系为:
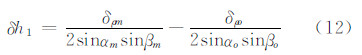
需要注意的是,式(12)中的αo与βo是通过模型求得的,不考虑它们与αm和βm的区别,再结合式(11),式(12)可以改写为:
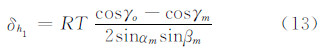
由于不知道海面相对于椭球面的高度,而海面与椭球面的差距最大不超过100 m[9],因此在实验和仿真分析中采用海面在椭球面上100 m的情况计算γo。
假设在理想情况下,式(6)和式(13)中的参数可以准确求得,用这两式可以消除动态性误差和信号平行误差。在实际情况中,上述参数可能求得不够准确(如式(13)中的γo),会因此剩余一些残余误差,但利用以上两式仍能大大削弱动态性误差和信号平行误差的影响。
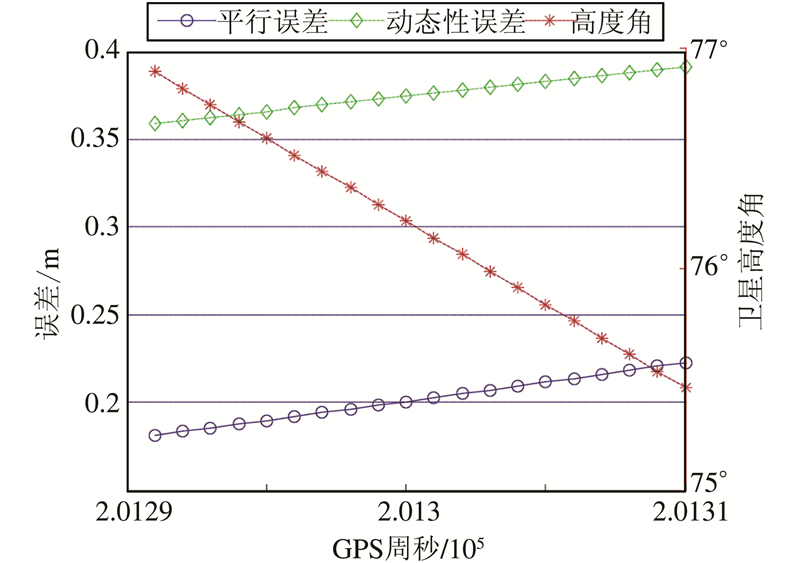
3 实例分析由于实际情况的复杂性,无法从表达式出发直接分析出误差量级大小。为此,本文以2004年11月16日UK-DMC(United Kingdom Disaster Monitor Constellation)在海洋上采集的部分数据进行了实验,表1给出了实验数据,两项误差的结果如图4所示。图4中,横轴表示GPS周秒,左边纵轴表示误差,右边纵轴表示镜面反射点处的卫星高度角。图4中圆圈实线表示假设信号平行引起的误差,大小约为0.2 m;菱形虚线表示动态性误差,误差在0.35 m以上。在这一过程中,高度角(星号虚线)变化不大,在75°左右。
| 发射机 | 接收机 | 接收机高度/km | 采样率/Hz | 数据长度/s |
| PRN22 | UK-DMC卫星 | 600 | 1 | 20 |
|
| 图 4 UK-DMC数据实验结果 Fig. 4 Results of UK-DMC Data |
从以上实例中可以得到这两项误差的具体大小,但由于该实验中观测时间短(只有约20 s),高度角变化也不大,而且也只采用了PRN22卫星的数据。因此,为了得到更一般性的结论,还需要对各种情况进行仿真分析。
4 仿真分析由于目前星载实验不多且实验数据较难获取,为了分析这两项误差的量级大小,本文采用仿真分析的方法。仿真数据如表2所示。接收机位于CHAMP和COSMIC低轨卫星的4个不同轨道上,分别与6颗不同轨道面的GPS卫星进行模拟。仿真时间为10 h,采样率0.1 Hz。模拟过程中有些时段的卫星与接收机不能构成反射事件,这种情况下将这两项误差设为零。
| 接收机载体 | 接收机高度/km | 发射机载体 | 采样率/ Hz | 仿真时间/h |
| CHAMP卫星 | 400 | |||
| COSMIC的1、4和6号卫星 | 800 | 6颗GPS卫星(6个轨道面,每个轨道面取一颗) | 0.1 | 10 |
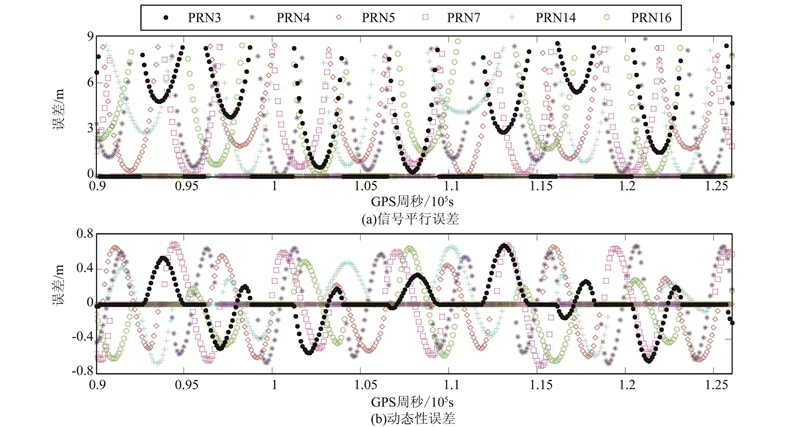
将模拟接收机搭载在CHAMP卫星上,接收来自PRN号为3、4、5、7、14和16的GPS卫星的直射信号与反射信号,如图5所示。采用的时段为2008年9月29日0~10时。图5(a)表示假设信号平行传播产生的误差,误差的绝对值最大可达到9 m左右;图5(b)表示各个采样时刻发射机机动态性引起的误差,误差在[-0.8,0.8] m内波动。
|
| 图 5 CHAMP卫星仿真结果 Fig. 5 Results of CHAMP Satellite |
由于COSMIC星座3颗卫星的仿真结果一致,在此以1号卫星进行分析,如图6所示。这颗卫星分别与PRN号为1、3、5、7、12和13的GPS卫星进行模拟,采用的时段是2013年6月29日0~10时。从结果中可以看出,信号平行传播引起的误差最大可达到15 m,发射机动态性引起的误差在正负1.5 m内波动。
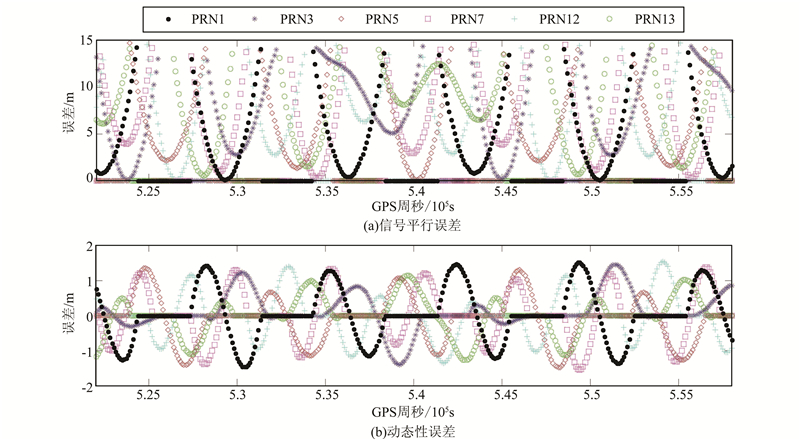
|
| 图 6 COSMIC的1号卫星仿真结果 Fig. 6 Results of Satellite NO.1 of COSMIC |
为了进一步研究这两项误差与镜面反射点处卫星高度角是否存在一定的联系,本文统计了仿真中4个轨道的数据,图7给出的是COSMIC6号卫星高度角与误差的统计结果。从图7(a)中可以看出,假设信号平行引起的误差随着高度角的增加而减小,在高度角为零附近的很小区间内,该误差有一个增加的过程,当图放大到一定程度时可以看到这一过程;从图7(b)可以看出,动态 性引起的误差与高度角之间没有明显的关系,而且它们之间不存在一对一的关系,但当高度角处于最小或最大时,误差接近零。对其他三个轨道的统计图分析也得到了类似的结论。
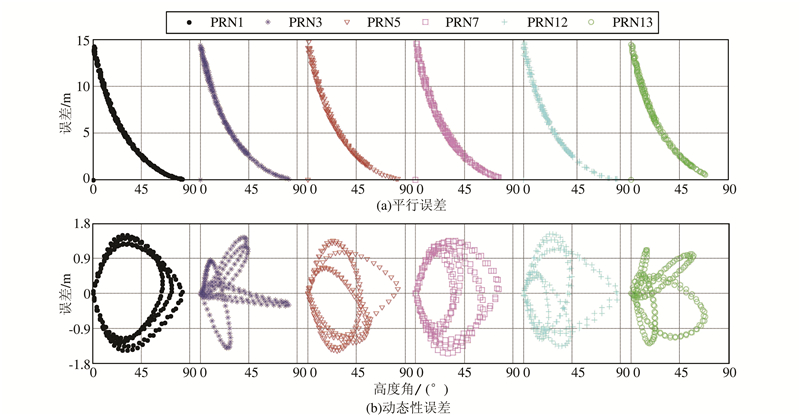
|
| 图 7 COSMIC 6卫星高度角与误差的关系图 Fig. 7 Relation Between Elevation Angle and Error in Satellite NO.6 of COSMIC |
通过本文的研究及实验与仿真分析,可以得到以下结论:(1)在目前星载GNSS-R测高中普遍没有考虑到动态性误差,仿真分析结果显示该误差最大可以达到m级,因此,在星载GNSS-R测高中,该项误差需要考虑;(2)当利用图2的几何模型进行GNSS-R测高时,除了考虑动态性误差,假设信号平行传播的误差也需要考虑。当海面高于椭球面时,该误差为正,例如实验和仿真中的结果,当海面低于椭球面时,误差为负;(3)目前可以通过精密定轨技术和事后精密星历获得高精度的轨道信息,对于这两项误差,都可以通过精密的卫星轨道信息按式(6)和式(13)进行校正。
致谢:CDAAC提供的仿真数据以及Gleason 公布的部分UK-DMC数据对本文的研究起到很大作用,在此一并感谢。
| [1] | Martin-Neira. A Passive Reflectometry and Interferometry System(PARIS): Application to Ocean Altimetry[J]. ESA Journal, 1993, 17:331-355 |
| [2] | Shao Lianjun, Zhang Xunxie, Wang Xin, et al. Sea Surface Wave Height Retrieve Using GNSS-R Signals[J]. Geomatics and Information Science of Wuhan University, 2008, 33 (5): 475-478(邵连军, 张训械, 王鑫, 等. 利用GNSS-R信号反演海波浪高[J]. 武汉大学学报·信息科学报, 2008, 33 (5): 475-478) |
| [3] | Liu Jingnan, Shao Lianjun, Zhang Xunxie. Advance in GNSS-R Studies and Key Technologies[J]. Geomatics and Information Science of Wuhan University, 2007, 32 (11): 955-960(刘经南, 邵连军,张训械. GNSS-R研究进展及其关键技术[J]. 武汉大学学报·信息科学报, 2007, 32 (11): 955-960) |
| [4] | Wagner C, Klokocnik J. The Value of Ocean Reflections of GPS Signals to Enhance Satellite Altimetry: Data Distribution and Error Analysis[J]. Journal of Geodesy, 2003, 77:128-138 |
| [5] | Kostelecky J, Klokoník J, Wagner C A. Geometry and Accuracy of Reflecting Points in Bistatic Satellite Altimetry[J].Journal of Geodesy, 2005, 79(8): 421-430 |
| [6] | Valencia E, Camps A, Park H, et al. Impact of the Observation Geometry on the GNSS-R Direct Descriptors Used for Sea State Monitoring[C]. Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 2012 |
| [7] | George A H, Cinzia Z. Theoretical Description of a Bistatic System for Ocean Altimetry Using the GPS Signal[J]. Radio Science, 2003, 38 (5):1-10 |
| [8] | Yang Dongkai, Zhang Qishan. GNSS Reflected Signal Processing: Fundamentals and Applications[M].Beijing: Electronic Industry Press,2012(杨东凯,张其善. GNSS反射信号处理基础与实践[M].北京:电子工业出版社,2012) |
| [9] | Semmling A M, Schmidt T,Wickert J, et al. On the Retrieval of the Specular Reflection in GNSS Carrier Observations for Ocean Altimetry [J]. Radio Science, 2012, 47: RS6007, doi:10.1029/2012RS005007 |
 2015, Vol. 40
2015, Vol. 40