文章信息
- 张秋昭, 张书毕, 刘志平, 郑南山
- ZHANG Qiuzhao, ZHANG Shubi, LIU Zhiping, ZHENG Nanshan
- 基于双差伪距/伪距率的GPS/SINS紧组合导航
- Tightly-coupled GPS/SINS Integrated System Measurement Model Based on Double-difference Pseudo-range/Pseudo-range Rate
- 武汉大学学报·信息科学版, 2015, 40(12): 1690-1694,1700
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1690-1694,1700
- http://dx.doi.org/10.13203/j.whugis20130349
-
文章历史
- 收稿日期: 2015-05-18

2. 国土环境与灾害监测国家测绘地理信息局重点实验室, 江苏 徐州, 221116
2 Key Laboratory for Land Environment and Disaster Monitoring of NASG, Xuzhou 221116, China
GPS/SINS组合导航系统可以充分发挥GPS(全球定位系统)和SINS(捷联惯导系统)各自的优势,实现高动态实时、高精度导航定位,已广泛应用于航空摄影测量、航空重力测量、移动测量系统等高精度定位和测姿工程中。目前,国内工程应用中普遍采用位置、速度匹配的松散组合形式,这种形式要求可视卫星必须大于等于4颗,并且在GPS定位和组合定位中往往采用两次卡尔曼滤波最优估计,导致观测量与观测时间相关,影响了组合导航的精度[1]。
GPS/SINS紧组合方式利用卫星的伪距/伪距率观测量直接参与组合导航解算[2, 3],可以有效避免松散组合方式中存在的问题,得到了众多学者的关注[4]。现有文献中对紧组合的研究大多集中于分析紧组合与松散组合方式的不同[5, 6, 7],紧组合方式的滤波方法等[8, 9, 10],对紧组合方式的观测模型的研究均集中于GPS的非差模型[11],GPS/SINS组合系统应用于高精度的测绘领域中,多采用事后差分技术。鉴于此,本文提出了一种基于双差伪距/伪距率观测值的GPS/SINS紧组合观测模型,并采用实测数据验证了该模型的正确性和有效性。
1 双差GPS/SINS紧组合系统状态方程与量测方程 1.1 状态方程当采用非差GPS观测值与SINS进行紧组合时,必须对卫星钟差、对流层延迟误差和电离层延迟误差进行建模处理,接收机钟差作为待估参数处理。在实际工作中,在接收机间(基准站和流动站)求一次差,可以消除共视卫星的卫星钟差,卫星星历误差、电离层延迟误差、对流层延迟误差等也可以相应削弱,在短基线导航定位中效果尤其明显。在卫星间求取双差,可以消除该历元的接收机相对钟差参数。若状态方程中不考虑载波相位未知的整周模糊度参数,双差GPS/SINS紧组合系统状态方程就仅剩下SINS误差方程,与松组合中的状态方程相同,具体模型可参考相关文献[12]。
1.2 双差伪距差量测方程在GPS/SINS紧组合导航系统中,经过 SINS递推可以得到载体某一时刻的位置[ xI yI zI ]T,同时由卫星系统播发的广播星历可以计算得到卫星i的位置[xSi ySi zSi ]T。根据欧氏距离公式,可以得到SINS与卫星i之间的伪距ρIi:
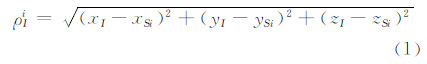
将式(1)在载体位置[x y z ]T处进行泰勒展开,仅保留一次项,则式(1)可以表示成:
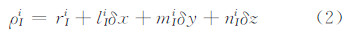
式中,rIi表示运载体的质心与卫星i中心的实际空间距离;lIi、mIi、nIi分别为卫星i对载体观测方向的三个坐标轴(站心坐标系)的方向余弦分量。
如果不考虑多路径效应,与SINS安装在一起的GPS接收机p观测到卫星i的伪距可以表示为:
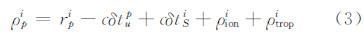
式中,rpi为GPS接收机p与卫星i的真实距离;cδtup为接收机p钟差引起的距离误差;cδtSi为卫星i钟差引起的距离误差;ρioni和ρtropi分别为电离层和对流层延迟引起的误差。
不考虑杆臂效应,则SINS与卫星i对应的伪距差观测方程为:
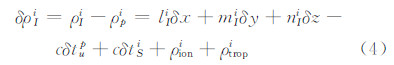
与式(4)类似,可以得到SINS与j卫星对应的伪距差观测方程为:
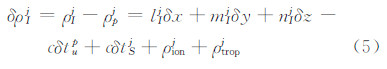
若观测过程中有基准站GPS信息可以利用,可以通过基准站GPS接收机q观测卫星i、j的伪距ρqi、ρqj。
将同步观测到卫星i的流动站观测值ρpi和基准站观测值ρqi之间求一次差得到ρpqi,同理可得到卫星j的站间单差观测值ρpqj。将单差观测值ρpqi和ρpqj星间求二次差,可得到双差观测值ρpqij。同理,也可得到SINS和基准站间的双差观测值ρIqij,将ρIqij与ρpqij求差,可以得到双差观测值的伪距差观测方程:
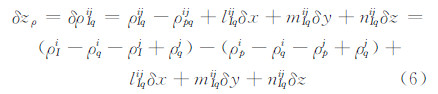
在GPS接收机能接收多普勒观测值的条件下,还可以利用多普勒观测值组成伪距率(也称多普勒)差观测量。将SINS推算的载体速度与GPS卫星i运行速度之间的伪距变化率表述为:
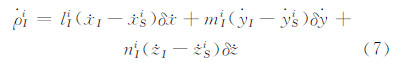
式中,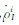 为载体中心(SINS中心)相对于卫星i的伪距变化率;lIi、mIi,nIi为卫星i观测方向对三个坐标轴的方向余弦;(
为载体中心(SINS中心)相对于卫星i的伪距变化率;lIi、mIi,nIi为卫星i观测方向对三个坐标轴的方向余弦;( 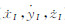 )为SINS经过力学编排得到的载体速度;(
)为SINS经过力学编排得到的载体速度;( 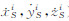 )为由广播星历计算得到的卫星i的速度;(
)为由广播星历计算得到的卫星i的速度;( 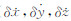 )为待求的载体。
)为待求的载体。
同理,安置在载体上的接收机p测得卫星i的伪距率为:
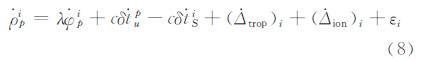
式中,λ为载波相位的波长; 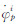 为接收机p相对卫星i的多普勒观测值;
为接收机p相对卫星i的多普勒观测值;  和
和 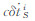 分别为接收机时钟漂移误差和卫星时钟漂移误差对伪距率的影响项;
分别为接收机时钟漂移误差和卫星时钟漂移误差对伪距率的影响项; 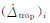 和
和 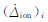 分别为对流层延迟变化率和电离层延迟变化率;εi为多普勒观测值的误差;其他项的定义可以参考式(7)。
分别为对流层延迟变化率和电离层延迟变化率;εi为多普勒观测值的误差;其他项的定义可以参考式(7)。
忽略杆臂效应,利用式(7)减去式(8),可以得到对应卫星i的非差伪距率差量测方程:
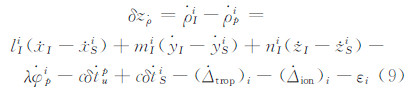
参考§1.1中的推导过程,可以得到双差伪距率差的量测方程:

式中, 和
和 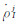 为SINS推算的结果与卫星星历求解速度得到的虚拟多普勒观测值;
为SINS推算的结果与卫星星历求解速度得到的虚拟多普勒观测值; 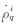 和
和 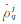 为基准站接收机q与卫星速度得到的虚拟多普勒观测值;lIqij、mIqij、nIqij为作差后的方向余弦项,可以根据近似坐标求取;
为基准站接收机q与卫星速度得到的虚拟多普勒观测值;lIqij、mIqij、nIqij为作差后的方向余弦项,可以根据近似坐标求取;  为待求的载体速度的改正数,其他类似符号的含义可参考式(8)。
为待求的载体速度的改正数,其他类似符号的含义可参考式(8)。
考虑到双差观测值能有效消除轨道误差、钟差、大气层延迟误差等误差项,本文采用双差观测值进行GPS/SINS紧组合系统组合定位。
2.1 基于双差伪距差的量测模型利用双差GPS伪距作为原始观测量,量测方程为:
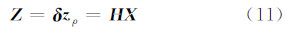
式中,
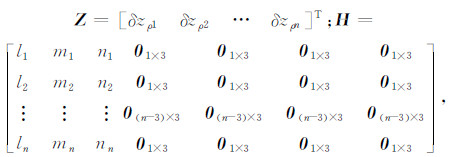
li、mi、ni为对应的卫星观测方向对三个坐标轴的方向余弦的双差系数项(i=1,2,…n),n为双差观测值的个数,等于共视卫星颗数减一。
2.2 基于双差伪距/伪距率差的量测模型利用双差GPS伪距、多普勒观测值作为原始观测量,量测如下:
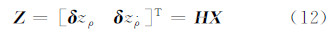
式中,
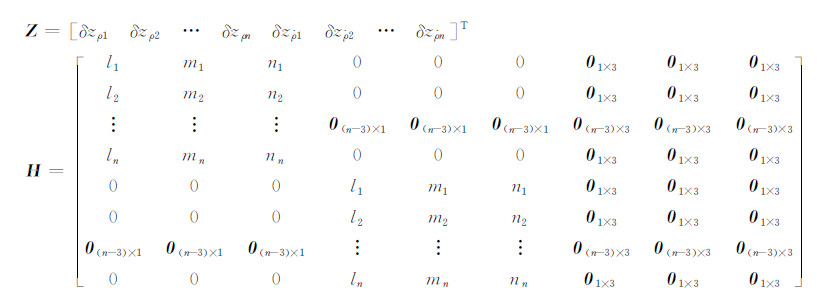
采集了一组车载GPS/INS导航实验数据,验证论文提出的观测模型的正确性。实验采用了两台GPS接收机和一台IMU(惯性测量单元)。其中一台GPS固定在楼顶作为基准站,另一台与IMU一起固定在车辆顶部。所用IMU为SPAN-CPT(三轴开环光纤陀螺和微机械加速度计),主要技术指标参数见表1,IMU采样频率为100 Hz,GPS的采样频率为1 Hz。初始位置误差为1.0 m,初始速度误差为0.1 m/s。
| ` | 陀螺 | 加速度计 |
| 零偏 | 20°/h | 5 mg |
| 随机游走噪声 | 0.067°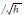 | 50 μg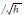
|
采用闭环反馈校正模式,每次测量更新并且反馈校正后状态向量均重新设置为0。初始状态协方差阵中位置误差对应的元素分别设为 (1 m)2、(1 m)2 和 (2 m)2; 速度误差对应的元素设为 (0.1 m/s)2; 姿态误差对应的元素设置与初始姿态精度有关,假设初始的俯仰角、横滚角和航向角误差分别设为5°、5°、30°;加速度计偏置和陀螺漂移对应的误差项可以根据表1给出的技术指标设定。
滤波方法采用标准UKF滤波方法。观测模型采用2种方案: 方案1,仅采用双差伪距作为观测输入; 方案2,采用双差伪距、伪距率作为观测值。
两种方案的处理结果如图1~图3所示。图1~图3中位置和速度的参考解为GPS高精度双差载波相位的解算结果(WGS84坐标系),因此组合导航输出结果的坐标系统也均为WGS84坐标系,下文中的XYZ坐标系均为空间直角坐标系,其三轴指向与WGS84坐标系框架一致;姿态的参考解为Waypoint-IE 8.30 软件经过双向滤波的解算结果。表2给出了两种处理结果的统计信息。
|
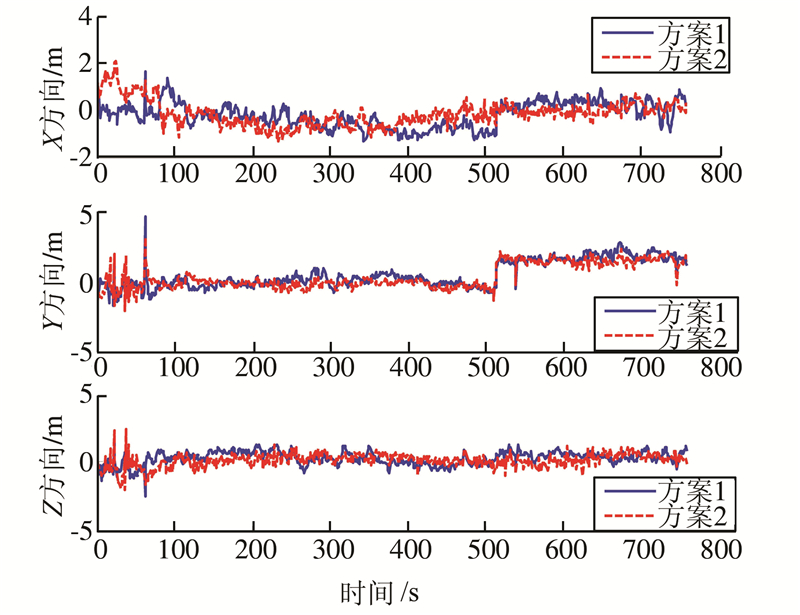
| 图 1 两种方案处理的位置误差 Fig. 1 Position Error of Different Schemes |
|
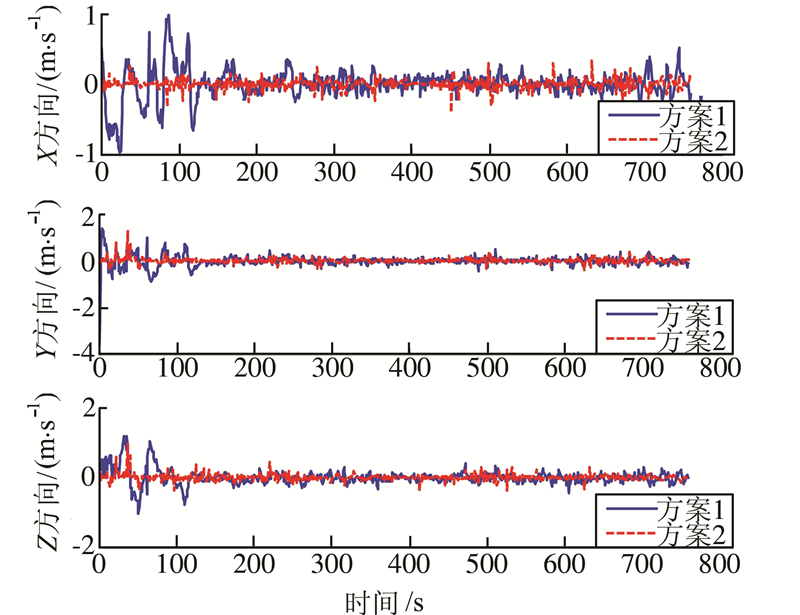
| 图 2 两种方案处理的速度误差 Fig. 2 Velocity Error of Two Schemes |
|
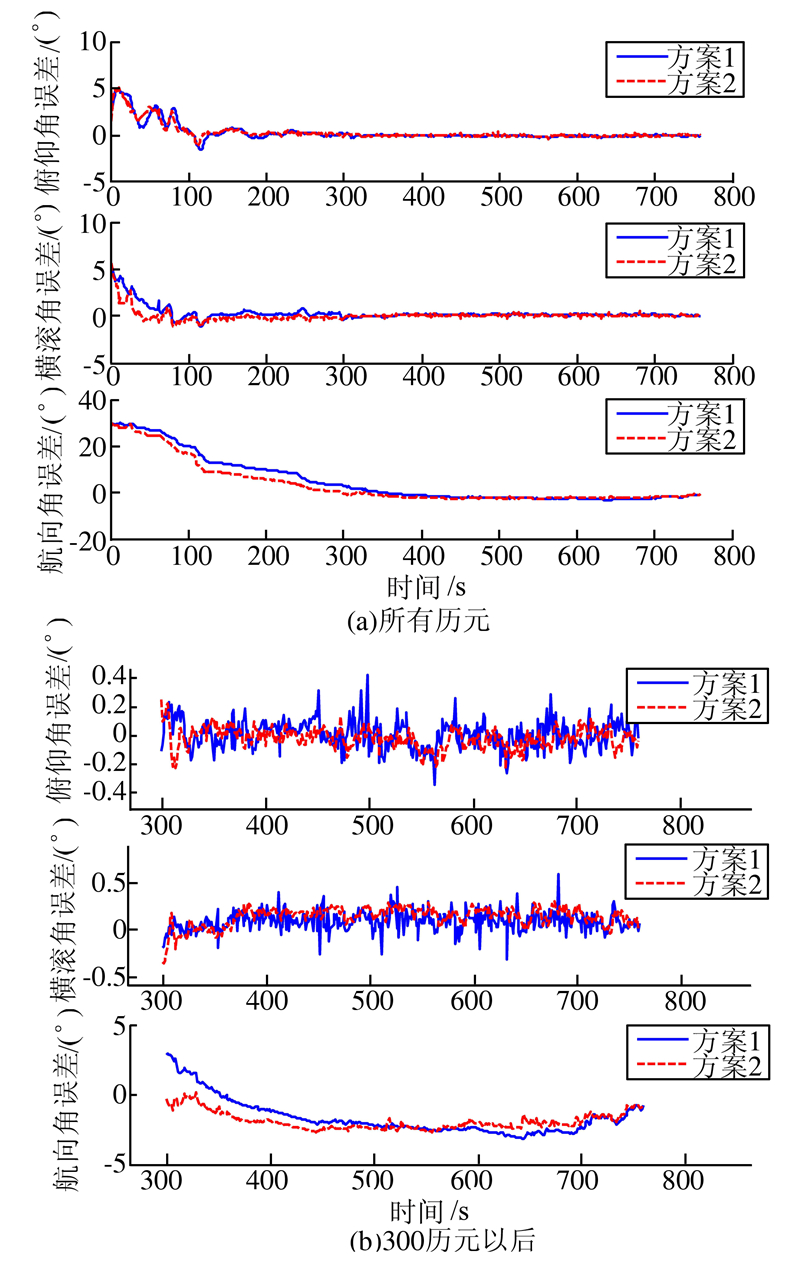
| 图 3 两种方案处理的姿态角误差 Fig. 3 Attitude Error of Different Schemes |
| 位置误差/m | 速度误差/(m·s-1) | 姿态角误差/(°) | 姿态角误差(300历元后)/(°) | |||||||||
| X | Y | Z | X | Y | Z | 俯仰 | 横滚 | 航向 | 俯仰 | 横滚 | 航向 | |
| 方案1 | 0.527 | 0.908 | 0.414 | 0.136 | 0.137 | 0.123 | 0.247 | 0.194 | 5.809 | 0.098 | 0.101 | 1.277 |
| 方案2 | 0.393 | 0.864 | 0.359 | 0.071 | 0.082 | 0.077 | 0.199 | 0.193 | 4.219 | 0.071 | 0.082 | 0.611 |
从图1可以看出,两种方案处理的位置误差和收敛速度差别不大,这是由于决定位置误差精度的主要因素为伪距观测量;图2中,方案2的速度误差和收敛速度较方案1有较明显的提高,这是由于双差伪距值只能直接解算出位置误差,方案1中的速度项的观测性较差,而方案2中引入了双差伪距率观测值,速度误差项的观测性得能到了较明显的改善,估计精度和收敛速度也得到了显著提高。
图3的结果表示,方案2中的姿态估计效果与方案1相比有所改善,是因为在GPS/SINS组合导航定位中,姿态角误差项是与速度项相互耦合的,引入了双差伪距率观测值,间接提高了姿态角估计的可观测性,精度和收敛速度均有所改善。另外,从图1和图3(b)中可以看出,位置误差和姿态角误差有明显的大波动,说明原始的伪距、伪距率观测值中有较明显的粗差存在。从表2中的定量统计信息可以得到,方案2比方案1的三轴位置精度仅提高了25.4%、4.8%和13.2%,尤其是Y轴方向精度较差(0.864 m),改善不明显。速度误差方法中,方案2的三轴速度误差分别为0.071 m/s、0.082 m/s和0.077 m/s,比方案1分别提高了47.8%、40.1%和37.4%,效果非常明显。统计全部历元的姿态角,发现误差较大,这是因为在滤波开始前设置的初始姿态角误差较大,存在一个收敛过程。滤波稳定后(300 s后)姿态角误差趋于稳定,方案2与方案1相比,姿态角精度有较明显的改进,尤其是航向姿态角误差收效速度提高了52.2%。这些定量分析均与图1~图3反映的定性结果一致。相对于仅采用双差伪距观测值的方法,采用双差伪距和伪距率原始观测值的组合导航精度都有所提高,速度和姿态收敛速度也更快。
4 结 语GPS/SINS紧组合导航中,量测方程直接关系着系统的滤波精度和可观测性。采用双差伪距和双差伪距/伪距率作为观测值均能实现组合导航紧组合模式的收敛。只采用伪距作为观测量时,系统的速度和姿态角状态 可观测性较差,导致速度和姿态角误差较大,且姿态角误差收敛较慢。将误差较小的伪距率引入观测量后,不仅系统的可观测性得到了改善,组合导航中速度和姿态角的估计精度也有显著提高。同时,姿态角误差收敛速度也得到了提高。如何抑制原始观测值中的粗差对估计精度的影响需要进一步研究。
| [1] | Zhou Kunfang, Kong Jian, Zhou Xiangrong. Analysis on Modular Navigation Ability of Coupling GPS/INS[J]. Journal of Chinese Inertial Technology, 2005, 13(6): 50-53 (周坤芳, 孔键, 周湘蓉. 紧耦合 GPS/INS 组合导航能力的分析[J]. 中国惯性技术学报, 2005, 13(6): 50-53) |
| [2] | Nassar S, Niu X, El-Sheimy N. Land-Vehicle INS/GPS Accurate Positioning During GPS Signal Blockage Periods[J]. Journal of Surveying Engineering, 2007, 133(3): 134-143 |
| [3] | Wendel J, Trommer G F. Tightly Coupled GPS/INS Integration for Missile Applications[J]. Aerospace Science and Technology, 2004, 8(7): 627-634 |
| [4] | Lu Yu, Hu Rui, Yang Yunchun. A Low Cost GPS/INS Tightly-coupled Navigation System[J]. Geomatics and Information Science of Wuhan University, 2011, 36(4): 481-485(鲁郁, 胡锐, 杨云春. 一种低成本 GPS/INS 紧耦合组合导航系统[J]. 武汉大学学报·信息科学版, 2011, 36(4): 481-485) |
| [5] | Zheng Xin, Fu Mengyin. SINS/GPS Tightly-coupled Integrated Navigation[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 33-37(郑辛, 付梦印. SINS/GPS紧耦合组合导航[J]. 中国惯性技术学报, 2011, 19(1): 33-37) |
| [6] | Tang Yonggang, Lian Junxiang, Wu Wenqi, et al. Tightly Coupled Integration Technology of RDSS Time Difference Carrier Phase/SINS and Its Experimental Research[J]. Journal of National University of Defense Technology, 2007, 29(2): 19-23(汤勇刚, 练军想, 吴文启, 等. 北斗载波相位时间差分/SINS 紧组合技术与实验研究[J]. 国防科技大学学报, 2007, 29(2): 19-23) |
| [7] | Georgy J, Noureldin A. Tightly Coupled Low Cost 3D RISS/GPS Integration Using a Mixture Particle Filter for Vehicular Navigation[J]. Sensors, 2011,11(4): 4 244-4 276 |
| [8] | Geng Y, Deurloo R, Bastos L. Hybrid Derivative-free Extended Kalman Filter for Unknown Lever Arm Estimation in Tightly Coupled DGPS/INS Integration[J]. GPS Solutions, 2011, 15(2): 181-191 |
| [9] | Zhao Sihao, Lu Mingquan, Feng Zhenming. Application of EKF and UKF in Tightly-coupled Integrated Navigation System[J]. Systems Engineering and Electronics, 2009, 31(10): 2 450-2 454(赵思浩, 陆明泉, 冯振明. EKF 与 UKF 在紧耦合组合导航系统中的应用[J]. 系统工程与电子技术, 2009, 31(10): 2 450-2 454) |
| [10] | Wang Jian, Liu Chao, Gao Jingxiang, et al. GNSS/INS Tightly Coupled Navigation Model Based on Robust EKF[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3):396-400 (王坚, 刘超, 高井祥, 等. 基于抗差 EKF 的 GNSS/INS 紧组合算法研究[J]. 武汉大学学报·信息科学版, 2011, 36(3): 396-400) |
| [11] | Zhao Lin, Xia Linlin, Cheng Jianhua.The Quadratic EKF Approach for AHRS/GPS Integration Based on the Pseudo Range, Pseudo Range Rate, Heading Measurement Model[J]. Journal of Harbin Engineering University, 2008, 29(10): 1 054-1 059(赵琳, 夏琳琳, 程建华. 伪距、伪距率、航向角观测模型的 AHRS/GPS QEKF 算法[J]. 哈尔滨工程大学学报, 2008, 29(10): 1 054-1 059) |
| [12] | Sun Hongxing, Yan Li, Jiang Weiping.Accurately Calculating Exterior Orientation Elements of Airborne TLS Using Kalman Filter to Process the New Combination of GPS Double-difference Carrier Phase and Doppler/INS Data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(7):642-645(孙红星, 闫利, 姜卫平. 高精度GPS差分载波相位多普勒/INS新型全组合解算机载TLS外方位元素[J]. 武汉大学学报·信息科学版, 2004, 29(7):642-645) |
 2015, Vol. 40
2015, Vol. 40



