文章信息
- 刘金钊, 柳林涛, 梁星辉, 叶周润
- LIU Jinzhao, LIU Lintao, LIANG Xinghui, YE Zhourun
- 利用重力异常数据构建重力梯度场的方法比较
- Comparison of Methods to Model Gravity Gradient Field Using Gravity Anomaly Data
- 武汉大学学报·信息科学版, 2015, 40(12): 1677-1682
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1677-1682
- http://dx.doi.org/10.13203/j.whugis20130797
-
文章历史
- 收稿日期: 2014-04-10

2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉, 430077
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, Wuhan 430077, China
在地质结构反演、地球资源勘探和重力辅助导航中,重力梯度数据作为重力位的二阶导数,对浅层地质结构密度变化十分敏感,其在空间的9个分量(5个独立分量)对密度异常体的反映也更加丰富,近年来得到了广泛应用。航空重力测量与以住的重力测量相比较,能大范围、快速地获取重力数据,其测量范围有效包括了以往重力测量难以达到的区域,重力数据的获取变得更加便捷,空间分辨率也有了大幅提高。然而,由于受到各种因素的制约,现阶段高精度重力梯度数据的测量和获取难以大范围实现,这也在一定程度上限制了地球物理勘探、地质资源调查和重力梯度辅助匹配导航等领域的进一步发展[1, 2]。
如何利用地形质量和重力数据解算得到高精度的重力梯度全张量一直是众多学者希望解决的问题,由于重力梯度对地表地形质量非常敏感,很多学者提出利用数字高程模型(digital elevation model,DEM)来解算重力梯度场[3, 4]。然而,由于密度测量的复杂性,利用DEM来解算重力梯度是通过假设密度为常数值来进行的,通常取岩石密度ρrock为2.67 g/cm3。这种做法忽略了地形质量密度变化和水准面以下密度异常在重力梯度场上的实际反映,造成了重力梯度最终解算结果的不准确[5]。重力异常数据能够反映地质体的密度变化,一些学者研究利用重力异常数据直接求取重力梯度全张量,克服了密度变化造成的缺陷[5, 6, 7]。此外,文献[8, 9, 10]提出了综合利用重力数据和DEM数据解算重力梯度场的方法,但数据融合方法的最佳适应性还有待深入研究和探讨。
本文根据位场理论中求解边值问题的数值应用方法,以斯托克斯平面积分、最小二乘配置和径向基样条函数为基础,直接利用重力异常数据恢复中长波段重力梯度全张量;通过构建理论模型证明了方法的有效性;利用澳大利亚实测重力异常数据求解了剖面重力梯度6个分量;最后,从功率谱分析的角度与Jekeli C的航空重力梯度功率谱密度模型进行了比对,并对三种方法进行了统计分析和讨论[11]。
1 方法原理 1.1 斯托克斯平面积分在物理大地测量中,斯托克斯公式用来求解经典重力位边值问题的解,由布隆斯定理和斯托克斯公式可以确定大地水准面上重力异常和扰动位的关系。考虑到重力梯度是位函数的二阶导数,随着距离的增加,重力梯度场的能量在空间上衰减得更加迅速;因此相对于重力异常,可将区域重力梯度看作局部效应,在平面坐标系下进行求解。斯托克斯平面积分利用自由空间重力异常计算扰动位的二阶导数来解算空间全张量重力梯度[12, 13]:
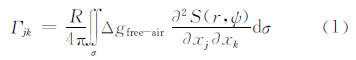
式中,Γjk为重力梯度分量;R是地球平均椭球半径;S(r,ψ)≈2R/l,为平面近似斯托克斯函数;xj,xk(j,k=1,2,3),为笛卡尔坐标系下方向。对式(1)的核函数进行离散化,得到平面近似的斯托克斯公式:
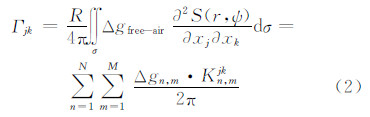
最小二乘配置是通过解算重力梯度与重力异常的互协方差函数矩阵,根据最小二乘配置由区域内的重力异常数据求解得到重力梯度全张量的一种方法[5]。
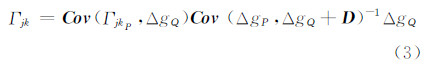
式中,Cov (ΓjkP,ΔgQ)为重力梯度与重力异常的互协方差阵; Cov (ΔgP,ΔgQ)为重力异常自协方差阵; D是观测噪声方差矩阵。
需要指出的是,利用区域内重力异常构建自 协方差矩阵时,对重力异常的空间分布并没有严 格的要求,重力异常数据可以是不同平面高度或同一平面高度内的非格网分布。这点区别于斯托克斯平面积分法求解重力梯度全张量,使得利用最小二乘配置时,源数据处理更加灵活方便,也保证了在格网化时降低时性的数据精度。
1.3 径向基样条函数定义Ω={ξ∈R3||ξ|=1}是R3空间里的单位球体,KA(ξ,ηi)是Freeden等构造的球面样条,该球面样条由距离球面上某点(ηi)的径向基函数来定义,而该径向基函数可以表示成勒让德多项式Pl(ξ,η)的无限级数。希尔伯特空间中的任一函数s(ξ)都可以用该球面样条来表示[14]。则空间点P的重力梯度全张量可表示成:
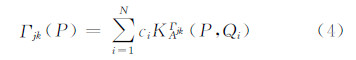
式中,KAΓjk(P,Qi)为重力梯度球面样条;ci为系数。KAΓjk(P,Qi),ci的解析表达式见文献[13]。
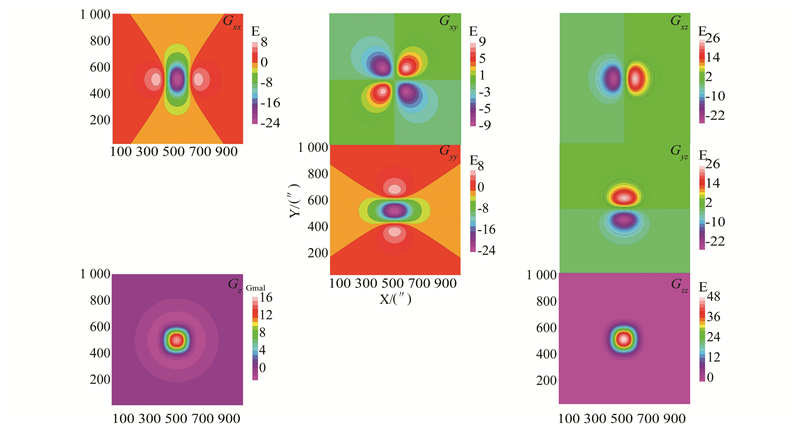
2 模型试验为了检验§1中介绍的斯托克斯平面积分、最小二乘配置和径向基样条函数三种方法解算重力梯度全张量的有效性,本文构造规则棱柱体模型来进行验证[15]。棱柱体长×宽×高为200″×200″×2 000 m(″为空间秒,1″≈30 m),位于区域范围为1 000″×1 000″的中心。棱柱体的重力异常和重力梯度理论值的计算结果见图1。
|
| 图 1 模型重力垂直分量及重力梯度全张量 Fig. 1 Vertical Component of Gravity Vector and Gravity Gradient Tensor of Model |
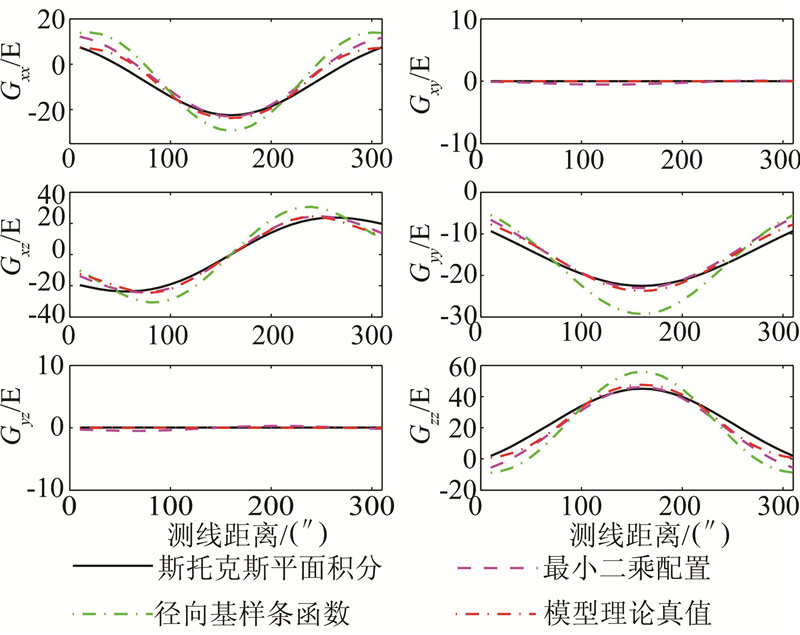
在1 000″×1 000″区域中选择了一条Y=500″,X=350″~650″,数据间隔为10″的测线,利用三种方法分别计算该测线上的6个重力梯度分量,并和模型得出的重力梯度进行对比。对比结果见图2,统计结果见表1。表1 中单位为E,1 E=10-9·s-2;M表示模型重力梯度理论值;S、L和R分别表示斯托克斯平面积分、最小二乘配置和径向基球面样条三种方法解算的重力梯度值;S-M、L-M和R-M是三种方法解算的重力梯度与模型重力梯度理论值的差。
|
| 图 2 三种方法解算的模型测线重力梯度及模型测线重力梯度理论真值 Fig. 2 Survey Line’s Gravity Gradients Derived from Three Methods vs. Model Theoretical Value |
| /E | ||||||
| 重力梯度差 | ΔΓ11 | ΔΓ12 | ΔΓ13 | ΔΓ22 | ΔΓ23 | ΔΓ33 |
| 标准偏差(S-M) | 2.114 5 | 0.007 1 | 3.566 7 | 1.159 7 | 0.001 3 | 3.126 0 |
| 标准偏差(L-M) | 1.205 1 | 0.222 6 | 1.230 8 | 0.403 9 | 0.280 6 | 1.484 3 |
| 标准偏差(R-M) | 4.466 7 | 0.004 7 | 4.778 9 | 2.731 1 | 0.008 2 | 6.442 3 |
从图2和表1中可以看出,斯托克斯平面积分和最小二乘配置两种方法相较于径向基样 条函数,解算得到的重力梯度值更加接近理论真 值。造成这种结果的原因可能是径向基样条函数是球面样条,更适合于解算球面大范围重力梯度场,对于小范围平面重力梯度场的解算,有一定的误差。另外,斯托克斯平面积分要求重力异常数据同一平面上呈格网化分布,而最小二乘配置和径向基样条函数则对重力异常数据的高度和水平分布没有严格要求,由此可见,三种方法在解算重力梯度方面互相补充,各有适用。
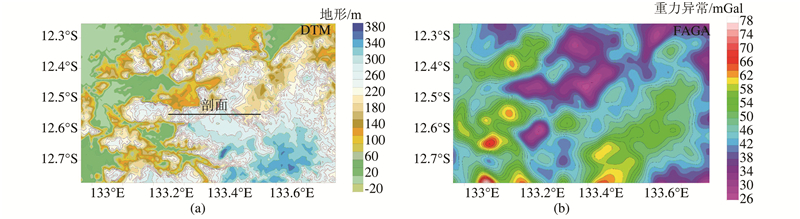
3 实测数据处理2003年8月27日~9月15日,荷兰Fugro公司和加拿大Micro Gravity公司在澳大利亚北领地进行了为期两周的重力测量实验,之后在Geoscience Australia网站上公布了60 s、80 s和103 s滤波后的重力异常数据[16]。笔者下载了这次航空重力测量的自由空间重力异常数据,并在测区中挑选了一条测线进行实验,重力异常数据和测线的信息见图3和表2。
|
| 图 3 测区地形和重力异常 Fig. 3 Terrain and Gravity Anomaly of Survey Area |
| 类型 | 纬度 | 经度 | 分辨率/(°) | 最小值/mGal | 最大值/mGal |
| 自由空间重力异常 | 12.773°N~12.253°N | 132.964°E~132.792°E | 0.004 | 26.8 | 77.07 |
| 测线 | 12.55°N | 133.25°E~133.55°E | 0.003 | * | * |
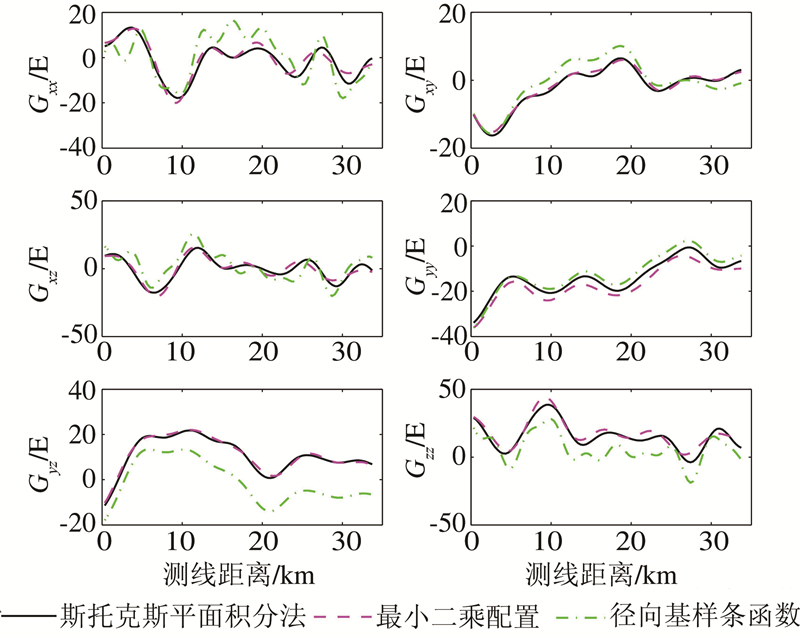
根据测区内的自由空间重力异常(这里使用的是80 s滤波后的重力异常数据),利用三种数值方法计算了测线的重力梯度6个分量值,计算结果见图4。
|
| 图 4 三种方法解算的测区测线重力梯度值 Fig. 4 Survey Line’s Gravity Gradients Derived from Three Methods |
从图4中我们可以看出,斯托克斯平面积分和最小二乘配置解算得到的重力梯度相当,而径向基样条函数解算得到的重力梯度(除分量 Gyy)与前两种方法解算结果相差较大。
由于缺乏实测重力梯度数据进行结果分析,本文求取了三种方法解算的重力梯度的功率谱密度(power spectral density,PSD)[17, 18],功率谱密度计算见式(5):
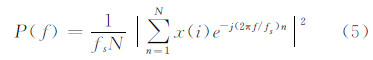
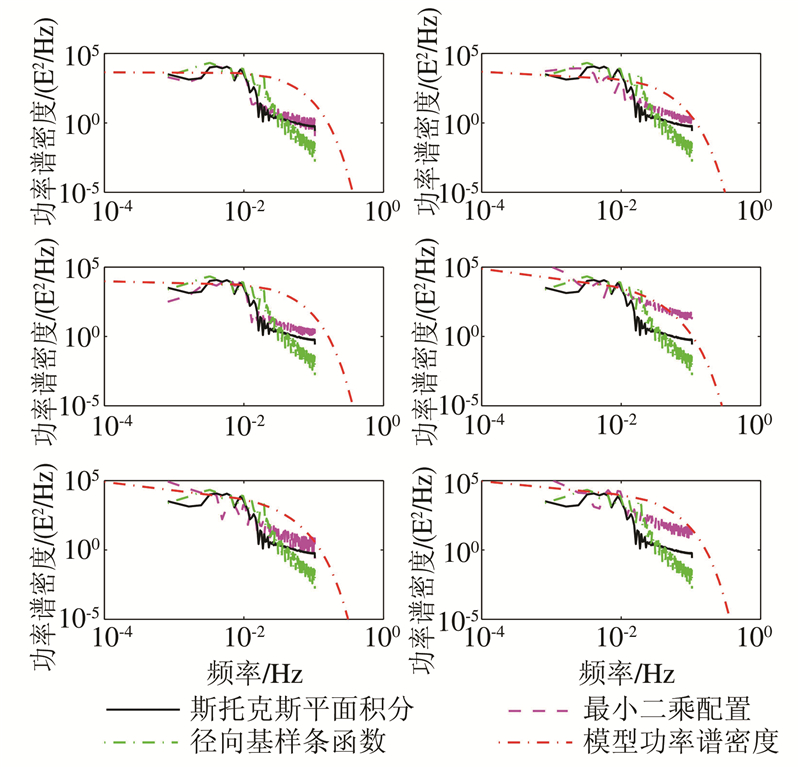
式中,x(i)(i=1,…,N)是原始信号向量;N是数据总数;P(f)是原始信号x(i)的功率谱密度;fs、f分别是采样频率和功率谱密度频率 。将所得功率谱密度结果与Jekeli航空重力梯度功率谱密度模型进行了比对[11]。结果见图5和表3。表3中,M表示模型重力梯度理论值;S、L和R分别表示斯托克斯平面积分、最小二乘配置和径向基球面样条三种方法解算的重力梯度值;PSD(ΔΓ)是解算的重力梯度与模型重力梯度理论值的差的功率谱密度。
|
| 图 5 三种方法解算的重力梯度功率谱密度与模型功率谱密度 Fig. 5 Gravity Gradients PSD Derived from Three Methods and Model PSD |
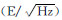 |
||||||
| 功率谱密度差 | PSD(ΔΓ11) | PSD(ΔΓ12) | PSD(ΔΓ13) | PSD(ΔΓ22) | PSD(ΔΓ23) | PSD(ΔΓ33) |
| 标准偏差(S-M) | 17.211 9 | 10.153 9 | 18.530 7 | 25.467 0 | 21.761 1 | 28.911 9 |
| 标准偏差(L-M) | 17.777 7 | 9.865 5 | 19.222 9 | 26.105 0 | 21.808 8 | 30.063 6 |
| 标准偏差(R-M) | 18.781 4 | 12.399 0 | 15.576 8 | 23.862 6 | 22.275 3 | 31.333 4 |
从图5和表3中可以发现,相对于径向基样条函数解,斯托克斯平面积分和最小二乘配置解算的重力梯度的功率谱密度与模型功率谱密度之差较小,这与§2中的棱柱模型分析结果相一致。从图5可以看出,频率小于0.01 Hz时,三种方法解算得到的重力梯度功率谱密度与模型功率谱密度误差较小,当频率大于0.01 Hz时,误差增大。因此,本文算法可直接利用重力异常数据恢复中长波段重力梯度场。
另外,应用重力梯度数据进行水准面以下油气矿产资源勘探时,需要做地形改正,去除水准面以上地形质量的影响。而重力梯度地形改正因背景噪声大,信噪比低,难以得到精确的改正后数据[19]。这时利用地形改正后的重力异常数据求解重力梯度就不失为一种间接有效的方法。
4 结 语本文根据物理大地测量中求解边值问题的数值应用方法,介绍了基于重力异常数据,利用斯托克斯平面积分、最小二乘配置和径向基样条函数解算空间全张量重力梯度数据的过程。构建了棱柱理论模型,同时处理了澳大利亚北领地实测自由空间重力异常数据,并将解算结果与国外成熟的功率谱密度模型进行了比对。无论是模型结果还是实测数据解算结果,都说明了三种方法解算重力梯度全张量的有效性。其中斯托克斯平面积分和最小二乘配置解算的重力梯度精度相当,优于径向基球面样条法解算结果。另外,斯托克斯方法处理重力数据时要求数据呈格网等间距分布(频域方法也要求数据呈格网等间距分布),而最小二乘配置与径向基样条函数则可以处理不同高度、任意间隔分布的区域重力异常数据,这就避免了观测数据格网化过程中高频信息丢失的问题,三种方法互相补充,各有适用。本文计算了实测重力数据解算得到的重力梯度的功率谱密度,并和Jekeli C航空重力梯度功率谱密度模型进行了对比,发现由于重力数据空间分辨率较低,解算得到的重力梯度功率谱密度和模型功率谱密度只在中低频波段(<0.01Hz)吻合较好,随着频率增大,结果变差。所以,建议利用本文方法处理高空间分辨率重力异常数据,构建精确的重力梯度数据库。
| [1] | Dransfield M. Airborne Gravity Gradiometry in the Search for Mineral Deposits[OL]. http://www.dmec.ca/ex07-dvd/E07/pdfs/20.pdf, 2007 |
| [2] | Zhang Changda, Dong Haobin. A New Develo pment Period of the Gravity and Magnetic Exploration[J]. Geophysical & Geochemical Exploration, 2010,34(1):1-7(张昌达,董浩斌.重力和磁力勘探进入新时期[J].物探和化探,2010,34(1):1-7) |
| [3] | Zhang Chijun. Determination of Vertical Gradient of Gravity Anomaly with Topographic Data[J]. Chinese Science Bulletin,1999,44(11):1 029-1 034 (张赤军.用地形数据确定重力异常垂直梯度[J].科学通报,1999,44(11):1 029-1 034) |
| [4] | Jekeli C,Zhu L.Comparison of Methods to Model the Gravitational Gradients from Topographic Data Bases[J]. Geophysical Journal International, 2006,166(3):999-1 014 |
| [5] | Zhu L,Jekeli C. Comparing Methods to Model the Local Gravity Gradients from Gravity Anomalies[C]. The Symposium of the International Gravity Field Service,Istanbul,Turkey,2006 |
| [6] | Kevin L,Mickus J, Homero H.The Complete Gravity Gradient Tensor Derived from the Vertical Component of Gravity:A Fourier Transform Technique[J]. Journal of Applied Geophysics, 2001,46(3):159-174 |
| [7] | Jiang F Y, Huang Y,Yan K.Full Gravity Gradient Tensor from Vertical Gravity by Cosine Transform[J]. Applied Geophysics, 2012,9(3):247-260 |
| [8] | Rózsa S,Tóth G. Prediction of Vertical Gravity Gradients Using Gravity and Elevation Data[M]. Berlin Heidelberg: Springer, 2005 |
| [9] | Zhu L, Jekeli C. Gravity Gradient Modeling Using Gravity and DEM[J]. Journal of Geodesy, 2009,83(6):557-567 |
| [10] | Liu Jinzhao,Liu Lintao,Liang Xinghui. Based on Measured Gravity Anomaly and Terrain Data to Determine the Gravity Gradients[J]. Chinese J.Geophys(in Chinese),2013,56(7):2 245-2 256(刘金钊,柳林涛,梁星辉.基于实测重力异常和地形数据确定重力梯度的研究[J]. 地球物理学报,2013,56(7):2 245-2 256) |
| [11] | Jekeli C. Statistical Analysis of Moving-base Gravimetry and Gravity Gradiometry[OL]. http://www.geology.osu.edu/-jekeli.1/OSUReports/reports/report_466.pdf, 2003 |
| [12] | Hofmann W B,Moritz H.Physical Geodesy[M]. Berlin Heidelberg:Springer,2006 |
| [13] | Zhu L Z. Gradient Modeling with Gravity and DEM[D].USA:The Ohio State University,2007. |
| [14] | Jekeli C.Spline Representations of Functions on a Sphere for Geopotential Modeling[OL]. http://www.geology.osu.edu/-jekeli.1/OSUReports/reports/report_475.pdf,2005 |
| [15] | Nagy D,Papp G,Benedek J.The Gravitational Potential and Its Derivatives for the Prism[J]. Journal of Geodesy, 2000,74(7-8):552-560 |
| [16] | Australia G.Geophysical Archive Data Delivery System[OL].http://www.geoscience.gov.au, 2012 |
| [17] | Jakob .Short-wavelength Spectral Properties of the Gravity Field from a Range of Regional Data Sets[J]. Journal of Geodesy, 2006,79(10-11):624-640 |
| [18] | Hu Guangshu. Digital Signal Processing[M]. Beijing: Tsinghua University Press, 2003(胡广书.数字信号处理:理论、算法与实现[M].北京:清华大学出版社,2003) |
| [19] | Tziavos I N,Sideris M G,Forsberg R.The Effect of the Terrain on Airborne Gravity and Gradiometry[J]. Journal of Geophysical Research:Solid Earth(1978-2012),1988,93(B8):9 173-9 186 |
 2015, Vol. 40
2015, Vol. 40


