文章信息
- 杨林, 万波, 王润, 左泽均, 安晓亚
- YANG Lin, WAN Bo, WANG Run, ZUO Zejun, AN Xiaoya
- 一种基于层次路划结构关系约束的矢量道路网自动匹配方法
- Matching Road Network Based on the Structural Relationship Constraint of Hierarchical Strokes
- 武汉大学学报·信息科学版, 2015, 40(12): 1661-1668
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1661-1668
- http://dx.doi.org/10.13203/j.whugis20140295
-
文章历史
- 收稿日期: 2014-04-10

2. 地理信息工程国家重点实验室, 陕西 西安, 710054;
3. 西安测绘研究所, 陕西 西安, 710054
2. State Key Laboratory of Geography Information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
道路网空间目标匹配是矢量道路地图集成、融合、更新及基于位置服务的导航等应用的核心和关键技术。针对道路网匹配问题,许多学者从几何特征、拓扑特征、语义特征及多特征综合的角度,通过相似性度量建立同名道路实体间的匹配关系[1, 2, 3, 4, 5, 6]。但局部相似性特征度量容易使道路匹配陷入局部寻优,因此,全局一致性思想在路网匹配中逐步发展[7, 8, 9, 10, 11],空间目标局部形态相似性的过度关注得到了较大改善。该匹配方法的主要问题表现在:(1)对非系统偏差较大的情形表现不佳。非系统偏差容易造成局部相似性度量特征失效,进而影响局部邻域结构的一致性调整策略。特别是在局部邻域结构相似的情况下,多个候选目标之间存在高度模糊性与不确定性,造成候选路段与实际匹配路段对应关系选取困难。(2)从局部入手直接以路段或者结点为单位进行匹配处理此类匹配情况时仍存在局限。
针对以上两点局限,本文参考人在识别同名道路时的视觉注意机制:(1)从突出到一般的原则。人在寻找同名道路时具有层次性,结构显著的道路比微小道路在视觉上更好辨认并易于确定匹配关系;(2)充分利用邻域结构特征辅助匹配。以层次路划结构关系来约束道路网的粗匹配与精匹配过程,有效克服非系统偏差造成的局部相似性特征度量失效问题。
1 算法思想路划是一组方向上延续、空间上连续的路段集合。目前概率松弛匹配法多采用局部路划策略进行邻域结构约束[9, 10]。局部路划是根据特定的终止条件形成的限定路划。在路段M∶N(M>0,N>0)匹配关系下,以M条路段为参照,在目标集中搜索满足路划特征的N条路段,称为局部路划约束。而全局路划是根据路划生成条件而产生的自然路划,与局部路划相比,不设定额外的终止条件,不受路段长度的制约。
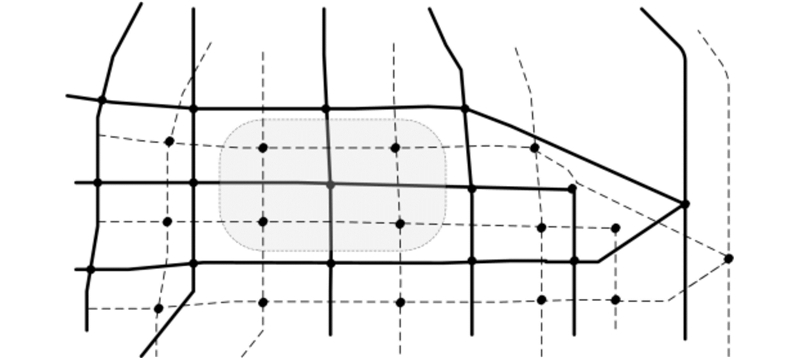
本文以自然路划为匹配单元,有利于识别空间中的显著结构,比路段或局部路划更易于建立匹配关系。图1中,在阴影区域,以路段或局部路划为匹配单元的相似性测度失效;若将视域范围扩大至自然路划,则有利于求解匹配关系。道路节点处于交错的路划结构之中,两条或更多自然路划可唯一确定一个道路节点。因此,路划结构关系是节点间关系的重要邻域上下文和约束条件。
|
| 图 1 局部路划与自然路划 Fig. 1 Local Stroke and Natural Stroke |
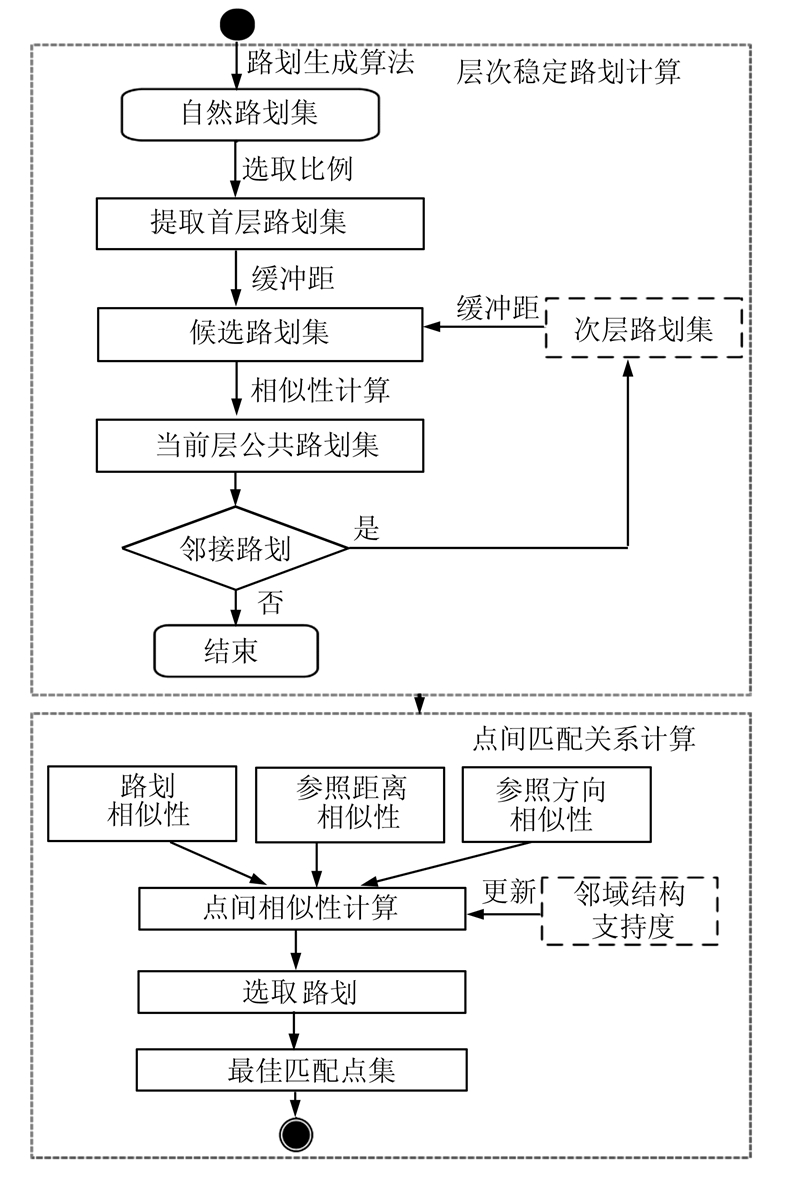
道路数据中的层次特征可以通过路划结构为人所感知。层次化的处理方法符合人们识别同名道路时从突出到一般的次序。构造“自然路划”匹配单元。首先,从道路结构空间中提取层次路划结构,计算每一层路划的公共部分,寻求较大粒度的路划结构间匹配关系,并建立分层稳定参照空间;然后,依层次路划结构关系将候选节点约束在相似路划之间,避免不满足路划约束条件的节点对的干扰,并将基于参照的空间关系度量融入相似性计算方法中;最后,利用概率松弛法的全局一致性调整优势对节点间的匹配关系进行迭代优化。算法过程如图2所示,包括层次稳定路划计算与点间匹配关系计算两大部分。
|
| 图 2 算法匹配流程 Fig. 2 Flowchart of Matching Method |
层次稳定路划结构计算包括路划生成、路划分层以及公共路划计算三个步骤。
1) 路划生成
因道路网络模型表达的需要,一条道路往往被道路交叉口打断成断续路段。路划生成则是利用判据规则将这一系列具有自然延伸形态的路段重新组织成连续道路。本文将相邻路段平均方向偏角小于45°的路段认定为同一路划。
2) 路划分层
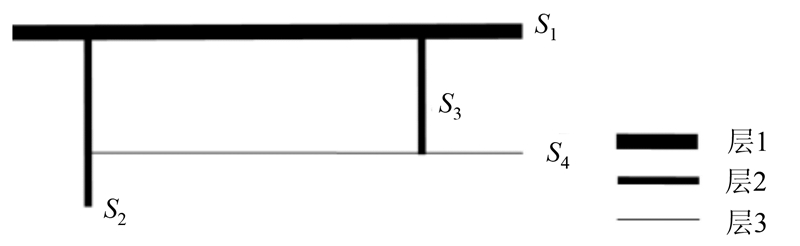
路划分层采用从高等级道路向下层辐射的方式,即首先选取高等级路划,与该层邻接的路划为下层路划,依此类推。图3为路网层次示意图,该区域有一条一层路划 S1 穿过,其邻接路划S2与S3为第二层路划集。同理,与S2、S3邻接的S4为第三层路划集。若路划在其所属的层内没有找到匹配对,则该路划降级到下一层继续参与匹配。
|
| 图 3 路网层次示意图 Fig. 3 Schematic Diagram of Road Network Hierarchy |
3) 公共路划计算
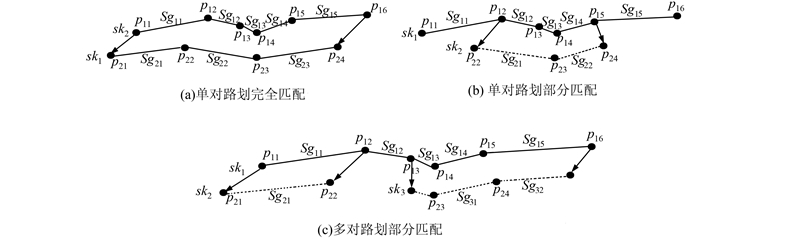
公共路划集为同层路划内部点和次层邻接路划提供参照。按照判据规则计算得到的路划在参照集与目标集中可能存在差异。为确保参照集的一致性,必须进行公共路划集的提取。公共路划的目的是计算在容差范围内两条相似路划的连续重叠部分。其匹配类型涵盖单对路划和多对路划两种,而单对路划则包含完全匹配和部分匹配两种情况,见图4。
|
| 图 4 公共路划匹配类型 Fig. 4 Matching Varieties of Public Stroke |
公共路划求解算法如下。
输入 参照路划集Set1、目标路划集Set2
输出 公共路划集PSet
变量说明 sign(公共路划开始标记)、first(公共路划首点)、last(公共路划尾点)、matchsk1、matchsk2(sk1、sk2的公共路划数组)。
算法步骤如下。
(1) 遍历Set1所有路划,对当前路划sk1的每一个路段sg1,基于其缓冲范围对目标路段进行相交及在内查询,形成结果集SegSet2。
(2) 若SegSet2=φ,即sk1在本层路划集中没有候选匹配集,则将sk1从Set1中移除,将sk1降级至下层路划集进行计算。
(3) 若SegSet2≠φ ,依次取出每一个路段,并获取该路段所属路划索引号,得到路划sk2。计算路划(sk1,sk2)之间的相似性与公共路划。若(sk1,sk2)已经计算过,则继续下一个路段。
(4) 置sign=0,mCnt =0。从sk1的首点p开始,若IspIn(BufAreask2)=true且sign=0,置sign=1,记first为当前点索引号,代表公共路划的开始位置;若IspIn(BufAreask2)=false且sign=0,表示未找到公共路划的首点,不做处理;若IspIn(BufAreask2)=false且sign=1,则停止搜索,在当前点附近容差范围内搜索最近的拓扑节点和顶点,拓扑节点优先级高于顶点,若无则根据sk2末点截取虚拟节点,并记last为当前点索引号;若IspIn(BufAreask2)=true,且sign=1,且当前点为尾点时,记last为当前点。当sign=1,且last有值时,第一段公共路划计算结束,将从first至last间的点计入matchsk1数组中。继续搜索下一段公共路划匹配对。
(5) 同理,处理sk2,得到matchsk2数组。计算matchsk1中每条路划与matchsk2中每条路划的相似性,并计入路划相似性矩阵。
(6) 当处理完Set1中全部路划,将Set1中每条路划计算所得{matchsk1、matchsk2}对加入PSet中。算法结束。
3 基于概率松弛法的点间关系计算1) 候选点集的计算
假设已分别从两幅待匹配道路网数据 A、B中计算得到所有层级的公共路划集PSet。Pai代表A中一个拓扑结点,ACS代表Pai经过的所有层级的路划集合(ACS⊆PSet),ACS={Sa1,Sa2,…,Sam},其中Sai表示Pai经过的某个层级的某一条路划,Sa={Pa1,Pa2,…,Pam}。BCS代表ACS在PSet中的对应路划集合(BCS⊆PSet)。Sb={Pb1,Pb2,…,Pbn}∈BCS为其中一条候选路划。PbSet为BCS的拓扑结点集合,以Pai为中心对PbSet进行缓冲区查询,得到Pai的初始候选结点集合PbSet。初始候选点集的选取在传统缓冲区法的基础上增加了路划约束条件,缩小了候选点集的范围。
2) 点间相似性计算
对A中每一个结点Pai计算其与PbSet中结点的初始概率。路划结构的关系相较于点对而言更易于确定,而点必定是路划上的端点或者内部结点,因而,点间匹配概率的设定将引入所在路划结构的约束,参考点与候选点所在的路划对之间的相似性越大,点间的匹配概率越大。另外,通过公共路划的计算为路划上的点提供一致的线性参照,故可将点在路划上的线性距离作为一个初始依据。因此,初始概率选取两个指标来综合度量:点所属路划的相似度Simsk与点的线性参照距离相似度Simsd。
路划的整体相似性由点所在路划的平均相似性来描述。假设n为点所在路划的个数,路划相似性由Simsk度量,点在路划上的线性参照距离由Simsd度量。点间的相似性则对点隶属全部路划的相似性度量取均值。设Pbj∈BCS为Pai的一个候选点,则Pai与Paj点间的相似性SimPai,Pbj如式(1)所示。式中,sPaik表示Pai所在的第k条路划。
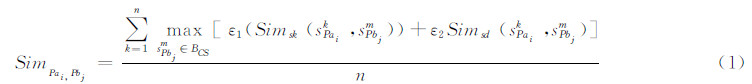
对Pai所隶属的每条路划sPaik而言,在Pbj所隶属的路划集中选取与sPaik相似值最大的路划sPajm值,并计算Pai与Pbj在sPaik与sPajm之上的Simsd值。其中,ε1取值0.6,ε2取值0.4。
地图存在局部差异时,绝对位置相似性的可靠性也随之降低。点在路划上的线性参照距离相似性Simsd采用点在对应路划上的位置到该路划起始点参照距离的相似性来描述:
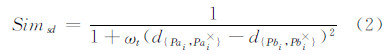
式中,ωt设定为误差因子的倒数,该值设定全局距离平均值;d表示参照距离。
路划整体相似性Simsk考虑利用几何相似性度量指标Simline来衡量。线形相似度Simline采用 Hausdorff距离进行度量。由于同名路划的生成方向具有不确定性,因此,在计算线形相似度时,通过计算两条路划正正(两条路划均从正向起算)、正反、反反、反正4个方向的线形相似度,选取最大相似值的路划对。
在上层公共路划确定的基础上,计算下层路划相似性时考虑将基于上层公共路划的相对差异融入相似性计算中。可以通过两个测度来定位新一层次的路划:(1)交点在公共路划上所处的相对参照位置,也即路划与上层公共路划的交点到起点间的累积距离长度与公共路划长度之比;(2)路划与公共路划的夹角。如式(3)所示,当所计算的两条路划不属于初始待配集(Layer≠1)时,则两条路划在上层路划上交点的相对位置相似度 Simloc,基于上层路划的相对方向相似度Simdir与路划相似度Simsk将共同作用于相似性度量。其中,ε1取值0.2,ε2取值0.4,ε3取值0.4。
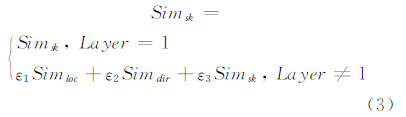
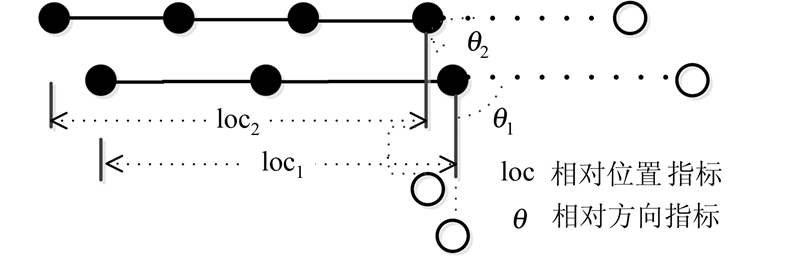
式中,Simloc为路划与上层路划的交点到上层路划起点间的累计距离相似度,计算方式与Simsd相似。即图5中 loc1与loc2的相似度。 当两条路划同时与上层多条同名路划相交时,需要计算平均位置相似度。同理,相对方向相似度Simdir,即两条路划基于上层路划的相对偏离角度,用待匹配路划与上层路划夹角的相似度来度量,即图5中θ1与θ2的差异,当两条路划同时与上层多条同名路划相交时,需要计算平均方向相似度。
|
| 图 5 相对指标示意图 Fig. 5 Schematic Diagram of Relative Indicator |
定义初始概率PPai,Pbj(0)为节点Pai与每一个候选点Pbj的匹配程度:
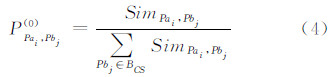
3) 迭代优化与匹配关系确定
通过点关系候选与相似性计算,较大概率的点间关系主要集中在路划结构相似的拓扑点间,在全局路划结构参照关系对点间关系的约束力较弱的特殊情况下,必须依靠局部结构的一致性来进一步增强细部关系,即通过局部邻域的一致性对匹配结果进行优化。利用式(5)进行迭代运算,定义当两次迭代矩阵变化小于阈值时退出迭代。

迭代通过邻居点对的整体支持度对初始概率进行调整。SPai,Pbj(r)描述了在第r次迭代时,点Pai与Pbj各匹配邻接点对其匹配提供的平均支持度。在进行邻居点集A×与B×选择时,在相同路划走向上搜索最小长度等价的节点对(Pai×,Pbj×),即搜寻符合条件的动态m阶邻居点对以适应路段的M∶N情况。迭代更新完成后,对点间关系进行选取。在点的相似性概率矩阵中对每个结点选取概率最大者,即匹配可能性最大的匹配对,并将其对应点记录从概率矩阵中剔除,继续下一个结点的选取。由于路划Sa'与Sb'中含有的内部节点个数不同,路段间的M∶N关系则可由点间1∶1关系推演得到。
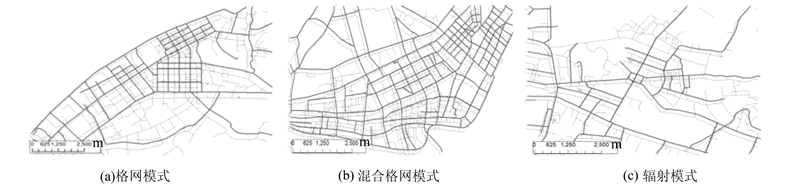
4 试验与结果分析为验证算法的有效性,本文选取一组武汉市道路数据进行验证。匹配道路数据源的时间分别是2006年与2011年,根据元数据显示,两份数据来自不同的单位。地图偏差在0~105 m区间内不等。同名道路还存在大量M∶N的匹配情况。试验选择三个典型区域:区域a为格网特征明显的区域;区域b为格网特征与非格网特征混合的区域;区域c为辐射模式区域。分别如图6(a)、6(b)、6(c)所示。具体信息如表1所示。
|
| 图 6 典型实验区域 Fig. 6 Classical Experimental Areas |
| 研究区域 | 源/目的 | 节点数 | 路段数 | 总长度/m | 路划数 |
| a | 源 | 123 | 184 | 100 148 | 54 |
| 目的 | 629 | 809 | 182 075 | 273 | |
| b | 源 | 259 | 404 | 92 657 | 96 |
| 目的 | 842 | 1 152 | 137 712 | 357 | |
| c | 源 | 91 | 111 | 50 218 | 42 |
| 目的 | 438 | 536 | 98 377 | 202 |
为确定首层路划的合理选取比例,以典型区域a为例进行测试。选取DR(Difference Rate)、HitRate、HitAvg三个指标来评价不同选取比例及缓冲区范围作用下路划与潜在候选解的差异分布关系。
1) 解的差异率DR:
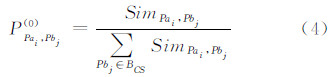
式中,Max为单条路划候选集中相似值最高者,记为参考值;V为单条路划候选集中除Max以外的其他解。
2) 使用HitRate单条路划在DR范围内命中的候选路划比率。在式(7)中,满足某一缓冲区范围的选取条件记为Conb,满足某一长度比例的路划选取条件记为Conp,满足某一DR范围条件记为Condr,M[Conp∩Conb]代表满足Conb与Conp的解的总数,N[Conp∩Conb∩Condr]代表满足Conb与Conp且落在某一DR范围内的解的数目。
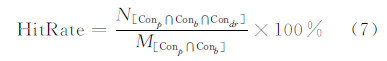
3) 使用HitAvg评价单条路划在DR范围内命中的候选路划数量平均值:
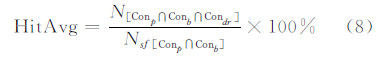
式中,Nsf[Conp∩Conb]表示参照数据中符合条件的路划总数目。
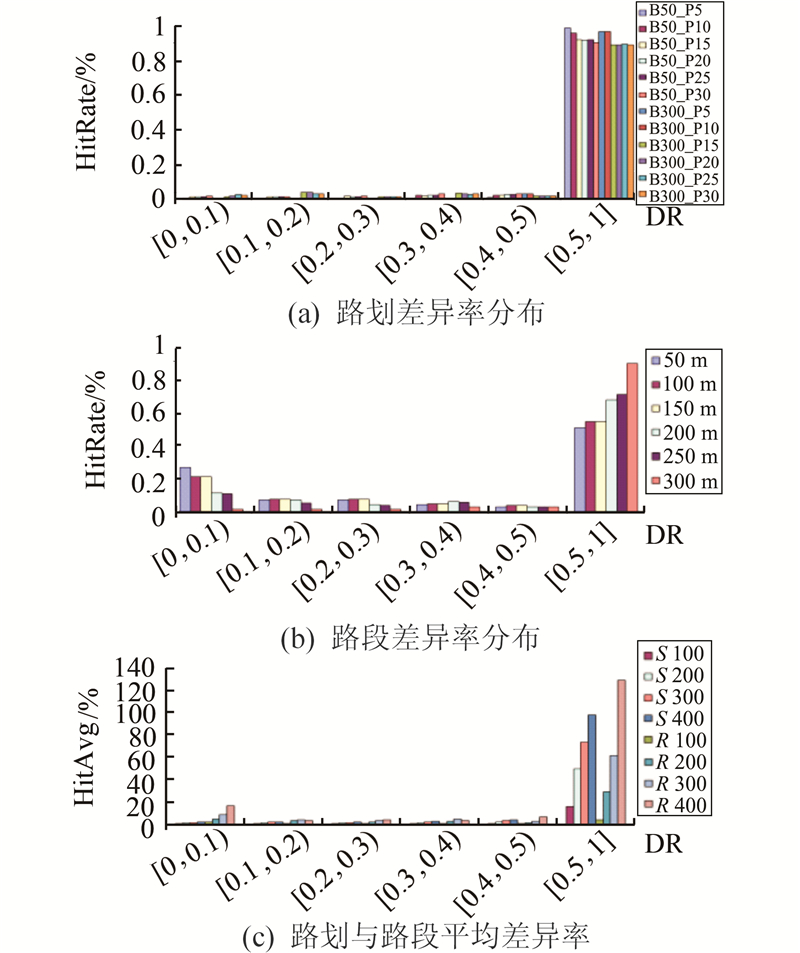
Conb选取50和300,单位为m。Conp取值5%~30%,计算HitRate与DR之间的分布关系,结果见图7(a)。图7中图例B50_P5代表Conb=50且Conp=5%。当Conb=50时,在(0.5,1]差异率范围内,HitRate均值达到0.92,说明90%以上的候选路划与其最大参照解具有显著几何差异。在[0,0.1)差异率范围内,HitRate均值仅达到0.01,说明候选路划与参照解非常近似的情况比例极少。当Conb=300时,其HitRate比率与DR范围之间关系的分布趋势与Conb=50时近似,说明缓冲区范围对于路划HitRate影响微小。
|
| 图 7 路划与路段差异率分布对比 Fig. 7 Difference Distribution Rate |
在单个DR区域内,HitRate值随着Conp取值的增大而增大。当Conp取值为5%、10%时,在[0,0.5)区间HitRate值趋近于0。说明路划及其候选路划之间的差异率显著,在[0,0.5)之间几乎没有分布,故进行首层路划比例选取时,使用10%作为首层路划选取的比例,能够保证首层路划匹配关系的稳健性与正确率。
与图7(b)的路段差异率分布关系图进行比较,发现路段差异率在[0,0.1)范围内时,HitRate均值达到图7(a)中相同范围内HitRate值的20倍。图7(c)展示了路划与路段在HitAvg指标上的差异。图7(c)中图例S代表路划,R代表路段,数值代表缓冲距大小。可以发现,随着缓冲距大小的增加,路段的HitAvg值显著增加,而路划的HitAvg值仅有微小增长,与上文中路划差异度分布对缓冲区大小不敏感的结论一致。可见,单个路段在缓冲区范围内的潜在候选数目远远大于单条路划在相同缓冲区范围内的候选数目,且候选路划与参照解之间的差异比路段的差异更加显著,以路划为单位进行相似性度量比以路段为单位进行相似性度量具有更好的辨识度,且对缓冲区大小的敏感度较低,这对于数据偏差较大的区域非常有利。
4.2 算法比较分析1) 算法选择
本文选取4种算法,从是否使用路划、使用局部路划、使用全局路划、使用层次策略4个角度,进行算法的对比分析,4种算法均采用概率松弛框架实现。具体见表2。
| 算法标记 | 使用路划 | 局部 | 全局 | 使用层次 |
| PR1 | 是 | 否 | 否 | 否 |
| PR2 | 是 | 是 | 否 | 否 |
| SPR | 是 | 否 | 是 | 否 |
| HSPR | 是 | 否 | 是 | 是 |
2) 试验环境及评价指标
本文基于MapGIS 10二次开发平台与Visual Studio 2010实现了上述4种算法,试验PC的处理器主频2.6 GHz,内存4 GB。
选取6个指标来评价匹配准确度:真乐观匹配 (正确匹配的要素)、假乐观匹配 (错误匹配的要素)、假消极匹配 (本应匹配而没有匹配的要素)及不确定匹配 (人工无法确定的匹配要素)。计算匹配的准确率P与召回率R为:
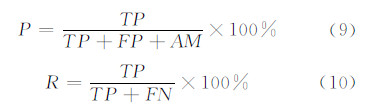
3) 试验结果
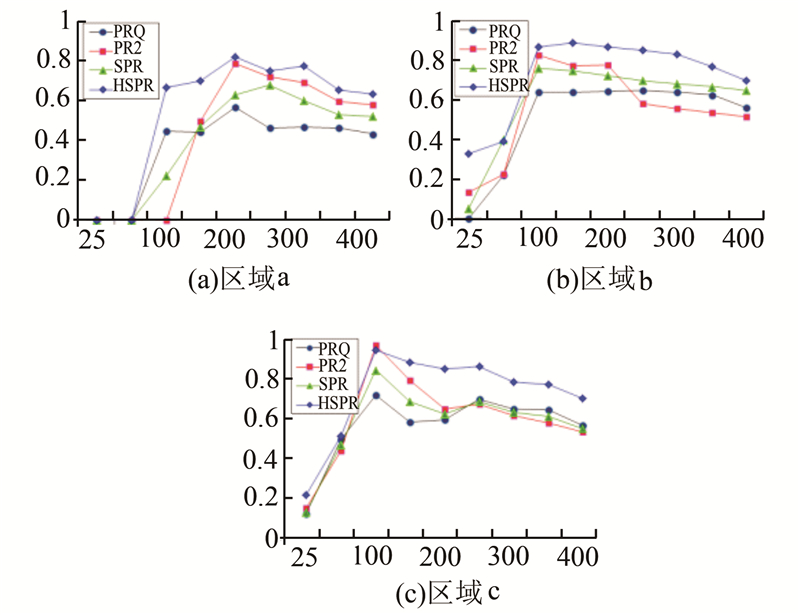
4种匹配算法的概率矩阵迭代终止阈值均设定为0.05。当满足终止条件时,不同算法的准确率和缓冲距的关系曲线如图8所示。对准确率进行比较发现,区域a最低、区域c最高、区域b居中。这说明规则格网模式在偏差较大时因其局部结构的高度相似性而难以获得较好的匹配效果,而辐射模式因局部结构辨识度高而易取得良好的匹配效果。
|
| 图 8 准确率与缓冲距关系曲线 Fig. 8 Relation Curve Between Accuracy and Buffer Distance |
试验结果显示,在三个试验区域内,PR2算法的最优解质量均优于PR1。可见,在概率松弛框架下,使用局部路划结构明显增强了匹配关系。HSPR算法的求解质量明显优于SPR算法。SPR算法直接建立全局路划之间的匹配关系,在不划分层次的情况下,中小路划之间的误匹配会影响节点之间的关系,降低准确率。而HSPR算法全局路划与层次策略相结合的方式对于匹配效果有着积极的影响。
区域b结果显示,HSPR算法的最优解比PR2算法提高6.3%,区域a内HSPR算法比PR2算法提高3.1%,区域c内HSPR算法与PR2算法的准确率持平。这是由于区域b的格网区域全局路划结构差异明显,而区域a的规则格网区域全局路划结构差异较小,区域c因局部路划结构与全局路划结构均具有明显差异而准确率较高。这说明,HSPR算法在全局路划差异显著的区域具有优势,PR2算法在局部路划差异微小的区域效果不理想。
从图8可以看出,缓冲距范围在[25,50]时,三区域内PR1算法均失效,无法获得匹配解,而其他算法也只取得较低的匹配率。随着缓冲距的增加,其值在[100,200]时,4种算法均获得P曲线的峰值。缓冲距在[300,400]时,4种算法准确率均呈下降趋势,PR2算法的下降趋势较快,HSPR算法的下降趋势平缓。说明PR2算法受缓冲距大小影响较大,而HSPR算法对缓冲距大小敏感度低。
当缓冲距为200 m时,HSPR算法在区域2内的单次迭代时间为17.65 s,迭代8次收敛。试验结果显示,路划生成时间占算法总耗时的平均比例仅为8%。故可知HSPR算法的效率受路划策略的影响非常微小。算法的时间复杂度为O(nn+sn·nsnlognsn),与同类算法相比效率理想。
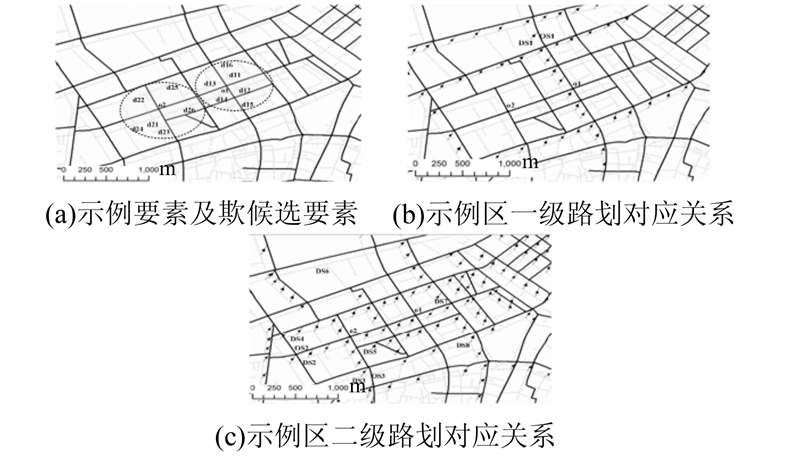
图9选取区域b的局部范围,展示了HSPR算法的匹配过程,以及层次路划的稳定参照和结构约束作用。在图9(a)中,节点 o1在候选区域中存在多个候选节点{d11,d12,d13,d14,d15,d16},从局部几何相似度以及一级邻域结构判定匹配关系都非常困难,极易产生误匹配。本文算法的匹配过程如下:图9(b)为一级路划匹配关系,图9(c)为二级路划匹配关系。{o1,d14}、{o1,d13}在首层路划计算过程中,受到路划{OS1,DS1}的约束进入候选集,且具有高的路划相似性分值。在二级路划计算过程中,{o1,d14}、{o1,d12}受到路划{OS2,DS2}的约束进入候选集,且路划相似性分值较高。而{o1,d13}、{o1,d12}因所隶属二级路划{OS2,DS7}、{OS2,DS5}相似度较低,故综合相似性值下降。{o1,d11}、{o1,d15}、{o1,d16}在首层没有与OS1匹配的路划,故首层计算中未进入候选集。在二级路划计算中因DS4、DS5、DS7均在OS2的候选范围内,则{o1,d11}、{o1,d15}、{o1,d16}进入候 选集,因路划DS2与DS4、DS5、DS7路划相似度值较低故而综合相似性值显著下降。上述6个匹配对要素间相似性值如表3所示,Sself为源要素与目的要素的局部结构的相似性值,取值非常接近。Ssk1表示一层路划相似值,Ssd1表示一层路划线性参照距离相似值,SimPai,Pbj表示源与目的综合相似值,节点为o1。在层次路划结构的约束下,{o1,d14}与其他5个匹配对之间的相似性值增加了区分度。可见,在局 部结构相似而难以辨识匹配关系时,层级路划的结构约束起了积极的作用。节点o2同理。
|
| 图 9 基于稳定路划结构的匹配过程 Fig. 9 Matching Process Based on Stable Stroke |
| O | D | Ssk1 | Ssk2 | Ssd1 | Ssd2 | Sself | SimPai,Pbj |
| o1 | d11 | 0 | 0.32 | 0 | 0.48 | 0.86 | 0.19 |
| o1 | d12 | 0 | 0.94 | 0 | 0.92 | 0.89 | 0.46 |
| o1 | d13 | 0.99 | 0.32 | 0.91 | 0.33 | 0.87 | 0.63 |
| o1 | d14 | 0.99 | 0.94 | 0.92 | 0.93 | 0.87 | 0.95 |
| o1 | d15 | 0 | 0.41 | 0 | 0.67 | 0.86 | 0.26 |
| o1 | d16 | 0 | 0.38 | 0 | 0.56 | 0.72 | 0.22 |
本文方法的特点在于依据道路层次生长结构建立路划结构的分层计算策略,并建立了以公共路划为参照的点间相似性计算方法。试验结果表明,使用路划为单位进行相似性度量时,候选路划与参照解之间的差异比路段更加显著,与参照解差异率在[0,0.1)范围时,单条路段命中的候选路段比率约是单条路划的7倍。且该方法对缓冲区大小的敏感度较低,对于数据偏差较大的区域非常有利。在概率松弛框架下,使用局部路划结构明显增强了匹配关系,然而该算法在局部路划差异微小的区域效果不理想。
| [1] | Hu Yungang, Chen Jun, Zhao Renliang, et al. Matching of Road Under Different Scales for Updating Map Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 451-456 (胡云岗,陈军,赵仁亮,等.地图数据缩编更新中道路数据匹配方法[J].武汉大学学报·信息科学版,2010,35(4) :451-456) |
| [2] | Zhao Binbin. A Study on Multi-scale Vector Map Objects Matching Method and Its Application[D]. Changsha: Central South University, 2011(赵彬彬. 多尺度矢量地图空间目标匹配方法及其应用研究[D]. 长沙:中南大学, 2011) |
| [3] | Sebastien M, Thomas D. Matching Networks with Different Levels of Detail[J]. Geoinformatica, 2008, 12: 435-453 |
| [4] | Cobb M, Chung M, Foley H, et al. A Rule-based Approach for the Conflation of Attributed Vector Data[J]. Geoinformatica, 1998, 2(1): 7-35 |
| [5] | Masuyama A. Methods for Detecting Appparent Differences Between Spatial Tessellations at Different Time Points[J]. International Journal of Geographical Information Sciences, 2006, 20(6): 633-648 |
| [6] | Liu Pengcheng, Luo Jing, Ai Tinghua, et al. Evaluation Model for Similarity Based on Curve Generalization[J]. Geomatics and Information Science of Wuhan University, 2012, 37(1): 114-117 (刘鹏程, 罗静, 艾廷华, 等. 基于线要素综合的形状相似性评价模型[J]. 武汉大学学报·信息科学版,2012, 37(1):114-117) |
| [7] | Song Wenbo, James M, Timothy L. Relaxation-based Point Feature Matching for Vector Map Conation[J]. Transactions in GIS, 2011, 15(1): 43-60 |
| [8] | Yang Bisheng, Zhang Yunfei, Luan Xuechen. A Probabilistic Relaxation Approach for Matching Road Networks[J]. International Journal of Geographical Information Science, 2012, 27(2): 319-338 |
| [9] | Volz S. An Iterative Approach for Matching Multiple Representations of Street Data[C]. ISPRS Workshop - Multiple Representation and Interoperability of Spatial Data, India, 2006 |
| [10] | Zhang M. Methods and Implementations of Road-Network Matching[D]. Munich:Technical University of Munich,2009 |
| [11] | Safra E, Kanza Y, Sagiv Y, et al. Ad Hoc Matching of Vectorial Road Networks[J]. International Journal of Geographical Information Science, 2013, 27(1): 114-153 |
 2015, Vol. 40
2015, Vol. 40



