文章信息
- 张晓楠, 江南, 张亚军, 颜玉龙, 崔虎平
- ZHANG Xiaonan, JIANG Nan, ZHANG Yajun, YAN Yulong, CUI Huping
- 一种利用空间布局构建统计制图符号的方法
- A Building Method of Statistical Cartographic Symbols by Using the Space Layout
- 武汉大学学报·信息科学版, 2015, 40(12): 1653-1660,1689
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1653-1660,1689
- http://dx.doi.org/10.13203/j.whugis20140395
-
文章历史
- 收稿日期: 2014-05-20

统计专题地图既是统计数据可视化成果表达的工具,是统计数据交互探索分析的工具,是统计数据信息传输的工具[1]。作为统计专题地图的最基本元素,统计制图符号搭建了制图者与用图者之间沟通的桥梁,实现了从制图者理解的数据到用图者认识的数据之间的信息传递。因此,探究一种灵活高效的符号构建方法显得十分重要。
纵观当前国内外学者对统计制图符号构建方法的研究,其实现途径大体分为基于视觉变量的构建方法和基于几何图元的构建方法。第一类研究中,以Bertin的图形构建理论和马耀峰的符号构成元素及设计理论[2]最具代表性。随着电子地图学理论和计算机技术的发展,特别是可视化技术的运用,传统视觉变量理论得到了较大的发展[3, 4, 5, 6, 7],对符号设计产生了深远影响。魏文展[8]通过视觉变量的数学定义,提出由有限视觉变量组成像元,再由有限像元构建地图符号的思路。张毅[9]从视觉元素出发建立统计地图符号的自适应生成模型。总体而言,这些研究均认为符号构成以视觉变量为主,构建方法都是对视觉变量进行不同程度的选取、组合或拓展;一旦视觉变量得到新的扩展,相应的构建方式就会受到冲击。第二类研究中,李伟[10]通过对基本图元的操作实现简单专题符号的设计与绘制。Schnabel[11]提出6种 图元配置法则,按一定的数据映射机制动态生成符号。吴小芳[12]以图元的形式组织符号,提出高效率的符号绘制方法。车森[13]设计的参数控制地图符号编辑器,点线面符号均采用基本图元组合而成。尹章才[14]提出基于SVG结构化的地图符号描述模型设计通用地图符号。总体而言,这些研究均倾向于图元的结构法则,未能考虑数据与图元或符号之间的映射关系,且对于几何图元的划分各异,难以涵盖形式多变的专题符号。
为此,有学者提出将视觉变量与图元进行有效集成,从而构建地图符号模型。颜玉龙[15]分析统计制图符号的图形结构及图元生成模式,提出面向快速制作的统计制图符号建造模型,本文方法就是在其研究基础上进一步延伸。通过对空间布局约束下的统计制图符号构成的分析,对其生成步骤进行剖析,提出利用空间布局构建统计制图符号的方法。这种全局控制下的符号构建方法,能够解决上述两类研究中存在的不足,不仅能够实现多指标复杂符号的自动生成,丰富符号的种类,增强符号的美观性,还能够兼顾制图数据与最终符号之间的映射关系,提高计算机生成符号的科学性和可控性。最后,本文设计并实现了统计专题图制作模块,结合实例验证了该方法的正确性和可行性。
1 空间布局约束下的统计制图符号构成分析 1.1 统计制图符号的涵义及分类统计制图符号是用来表达统计数据类型的专题地图符号。它依靠若干几何图元按照组合配置规则进行组织,依靠视觉变量与统计数据取得关联,传递统计数据的定量信息,实现专题数据的可视化。
根据表达的地理要素及数据指标的特点,将常见的统计制图符号分为单一统计符号、关系统计符号和集合统计符号三类,部分典型符号如图 1所示。

|
| 图 1 典型统计制图符号的分类 Fig. 1 Classification of Statistical Graphics Symbol |
单一统计制图符号是指表征单要素单指标的统计符号,由单个图元或视觉变量构成,通常具有分类特征、分级特征和数值特征;关系统计制图符号是指表征单要素多指标的统计符号,由多个图元或视觉变量构成,指标之间通常存在相关关系,包括对比关系、结构关系、扩张关系等;集合制图统计制图符号是指表征多要素多指标的统计符号,多个指标之间可能不存在任何关系。集合统计符号是对上述二者的有机结合,其各个统计符号之间相互独立。
1.2 统计制图符号的空间布局集合统计符号的结构复杂多变,制作难度较大,不便于实现符号的自动构建。为此,可利用空间布局的方法来有效解决这一问题。
布局的概念最早由Kantorovich[16]提出,用以描述给定的一个布局空间和若干待布物体,是将待布局物体合理地摆放在空间中以满足必要的约束的过程[17]。空间布局的相关概念和理论衍生自布局在城市规划、艺术设计等领域中的应用[18],是对地理空间区域中布局物体之间相对位置关系的组织与安排。
统计制图符号布局可以看作是空间布局的一种微观表现形式,几何图元及其视觉变量是统计符号待布局的物体。因此,统计制图符号的空间布局就是对视觉变量或几何图元的组合配置关系进行的统一描述,包括图元布局和视觉变量布局两个层次。
1) 图元布局
图元布局作为几何图元在符号空间中的定位框架,描述几何图元在组合配置过程中的相互位置关系,分为简单布局、线性布局、中心布局、格网布局和分层布局,如图 2所示。

|
| 图 2 统计制图符号的图元布局 Fig. 2 Figure Elements of Statistical Graphics Symbol |
2) 视觉变量布局
简单布局仅包含单个图元,无须进行图元的配置操作。线性布局描述沿某一直线方向排列的几何图元的配置。中心布局描述沿某一中心点顺时针或逆时针排列的几何图元的配置。格网布局描述呈网状排列的几何图元的配置。分层布局描述不同层面间具有压盖关系的几何图元的配置。此外,不同类型布局间可以相互嵌套,共同约束几何图元的排列配置。
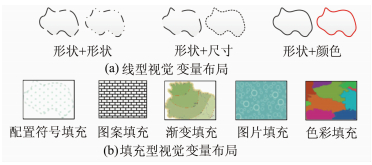
视觉变量布局与图元布局不同,主要描述视觉变量之间的组合关系,而不是相对位置关系。它分为线型视觉变量布局和填充型视觉变量布局,如图 3所示。
|
| 图 3 统计制图符号的视觉变量布局 Fig. 3 Visual Variable Layout of Statistical Graphics Symbol |
线型视觉变量布局主要为几何图元的轮廓线绘制服务,由形状、密度、色彩、尺寸和透明度构成。填充型视觉变量布局分为配置符号填充、图案填充、渐变填充、色彩填充及图片填充等,每种填充型视觉变量布局包含的视觉变量与对应的视觉变量组合相一致。
1.3 统计制图符号布局的内部构成为了实现统计制图符号的自动生成,需要在前述空间布局的框架下研究其内部构成。统计制图符号的布局内部由几何图元和视觉变量构成。
1.3.1 几何图元几何图元是构成统计制图符号布局的基本图形单元。本文概括出圆形、扇形、扇环、矩形、面域图元、三角形、多段线和规则多边形等8类几何图元,如图 4所示。这里主要对新增的面域图元进行说明。

|
| 图 4 统计制图符号的基本图元 Fig. 4 Basic Figure Elements of Statistical Graphics Symbol |
面域图元只针对呈面状的统计制图符号而言,是组成该类符号的唯一几何图元。它的图形轮廓并不固定,与符号所代表的面状要素的轮廓保持一致,内部填充则由图元的填充模式决定(颜色填充或配置符号填充)。面域图元专门为构建面状统计制图符号服务,它能有效地将面状符号与点状或线状符号等同对待,使得三者在相同图元框架下得以统一。
每个基本图元均包含一个图元控制点(图元上的黑点)和图元方向(图元箭头所示方向)。各个图元还包含其他几何参数,如扇形还需要起始角度、跨度和半径三个参数才可唯一确定。
1.3.2 视觉变量视觉变量也称图形变量,是图形符号之间具有的可引起视觉差别的最基本的图形或色彩因素的变化[19],是地图上的最小图解单元。目前对视觉变量的研究较为深入,此处不再赘述。为了便于实现统计制图符号的计算机绘制,本文对统计制图符号中的基本视觉变量进行了界定,它们是形状、尺寸、色彩、密度、方向、透明度、图案,相关解释从略。
2 空间布局约束下的统计制图符号构建方法 2.1 统计制图符号的描述与组织文献[15]在一定程度上揭示了统计制图符号的构建规律,但未能对其所需的参数进行详尽分析,为符号绘制的计算机实现带来不便。为此,本文给出空间布局约束下统计制图符号的形式化描述方法,为最终的符号绘制奠定基础。
图元布局的形式化描述参数如表 1所示,其表示方法如下,其中{}代表集合关系:
| 布局对象 | 描述参数 | 示例 | |||||
| 控制点 | 偏移量 | 布局方向 | 图元个数 | 排列方向 | 其他参数 | ||
| 简单布局 | 多边形的中心 |
dX∈(-∞,+∞) dY∈(-∞,+∞) |
0≤α≤360 | N = 1 | 无 | 无 |  |
| 线性布局 | 起始点 |
dX∈(-∞,+∞) dY∈(-∞,+∞) |
0≤α≤360 | N ≥ 1 | 水平或垂直 | 图元间隔 |  |
| 中心布局 | 圆心 |
dX∈(-∞,+∞) dY∈(-∞,+∞) |
0≤α≤360 | N ≥ 1 | 顺时针或逆时针 | 起始方向、布局跨度 | 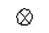 |
| 格网布局 | 方形的左下角点 |
dX∈(-∞,+∞) dY∈(-∞,+∞) |
0≤α≤360 | N ≥ 1 | 水平或垂直 | 水平和垂直方向排列数 |  |
| 分层布局 | 各层布局中心点 |
dX∈(-∞,+∞) dY∈(-∞,+∞) |
0≤α≤360 | N ≥ 1 | 垂直 | 层数、深度 |  |
图元布局 = {控制点(P)、偏移量(O)、图元个数(N)、排列方向(D)、其他构建参数(E)}。
例如,对中心布局的形式化可表示为:
中心布局 = {P = 圆心,O = {dX,dY | dX ∈ (-∞,+∞),dY∈ (-∞,+∞)},N∈ Z+,
D={d | d = 0(顺时针),d = 1(逆时针)},α∈[0,360],Sspan∈[0, 360]}。
视觉变量布局仅包含了视觉变量之间的组合关系,其形式化描述方法可以采用文献[8]中的方式。
由此,给出统一的空间布局约束下统计制图符号形式化描述方法({}代表集合关系):
统计专题符号 = {符号属性、图元布局};
符号属性 = {符号编码、符号名、符号类型、符号定位点……};
图元布局 = {图元布局属性、图元、图元布局};
图元布局属性 = {名称、类型、控制点、偏移量……};
图元布局 = {图元};
图元 = {图元属性、线型视觉变量布局、填充型视觉变量布局};
图元属性 = {名称、类型、控制点、偏移量……};
线型视觉变量布局 = {形状、色彩、尺寸、透明度};
填充型视觉变量布局 = {配置符号填充、纹理填充、渐变填充、色彩填充、图片填充};
尺寸 = {尺寸变量处理模型};
……
根据上述形式化描述方法,采用XML结构化语言实现统计制图符号的组织与存储。为减少信息冗余,只存储符号可变的描述信息。布局约束下的统计制图符号,可变的描绘信息包括符号构成元素的层次关系、符号构成元素与指标的对应关系、符号及符号构成元素的相关属性三部分。其中,符号构成元素的层次关系本身可以通过XML语言的结构特性表达,符号构成元素与指标的对应关系以及相关属性可通过在标记对象中建立属性的方式进行关联与存储。符号创建时图元的具体个数由对应指标包含的字段个数确定。符 号编码由五位数字构成:第一位代表专题地图表示方法,第二、三位代表指标类型,最后两位代表指标数量。部分符号存储的实例如图 5所示。

|
| 图 5 统计制图符号XML组织存储实例 Fig. 5 XML Organization Storage Instance of Statistical Graphics Symbol |
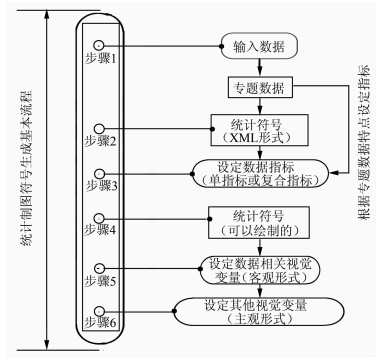
本文设计了统计制图符号计算机生成的基本流程,如图 6所示。具体步骤为:(1) 根据制图目的和要求,载入专题数据图层。(2) 根据用户所选表示方法获取XML形式的结构化符号。(3) 选择若干字段创建相应指标(单指标或复合指标)。(4) 根据指标信息动态地创建用于绘制的统计符号。(5) 对客观形式的视觉变量设定对应的数据处理模型并计算。(6) 根据符号美观性要求,自由设置主观形式的视觉变量。经过上述6个步骤,可生产统计制图符号。
|
| 图 6 统计制图符号计算机生成的基本流程 Fig. 6 Basic Process of Computer Generated Statistical Graphics Symbol |
按照以上生成流程,结合符号的描述与组织方法,详述统计制图符号的构建方法。主要有三个步骤,如图 7所示。

|
| 图 7 主要构建步骤 Fig. 7 Main Construction Steps |
统计制图符号的视觉变量与专题数据的关系密切。视觉变量是表征专题数据属性特征的主要手段,而专题数据控制视觉变量的空间布局形式。根据其表现形式,视觉变量的构建方法分为两部分,如图 8所示。客观视觉变量通过与之关联的数学处理模型实时计算而得到具体数值,体现了符号生成过程严谨的科学性;主观视觉变量通过符号整体美观性与协调性的原则设置相应数值,体现了符号生成过程灵活的艺术性。

|
| 图 8 视觉变量的构建方法 Fig. 8 Construction Method of Visual Variable |
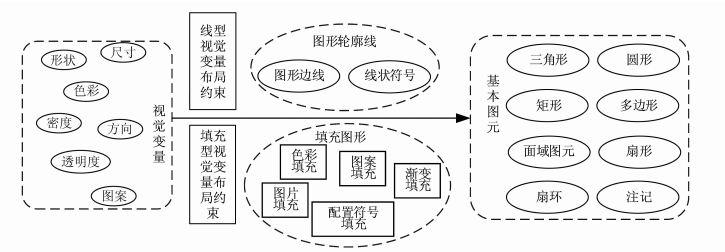
根据基本图元的组成结构,图元构建方法分为两部分,如图 9所示。图形轮廓线在线型视觉变量布局约束下进行构建,而填充图形在填充型视觉变量布局约束下进行构建。
|
| 图 9 布局约束下的图元构建 Fig. 9 Construction of Figure Elements under the Restriction of Layout |
1) 图形轮廓线的构建
图形轮廓线包括图形边线和线状符号。图形边线总是作为填充图形的附属边线存在,而线状符号作为一类符号单独存在,它们的构建方法有所不同:(1) 对于图形边线,以形状表征专题要素的数量和等级特征,且使用实线。范围法中用到的图形边线,或表示特定含义的边线(如正在变化过程中的事物),可用虚线。图形边线被视作填充图形的附属物而处于符号的较低层面,色彩素雅淡薄,不用透明度变量。(2) 对于线状符号,以形状、色彩、方向表征专题要素的质量和数量特征,以尺寸表征等级特征。当色彩鲜艳浓重时,用透明度表征等级特征。
2) 填充图形的构建
在不同填充型视觉变量布局的约束下,视觉变量经过有机组合配置以完成填充图形的构建,并表征专题要素的数据特征,如表 2所示。
| 布局对象 | 专题要素特征 | ||
| 质量特征 | 数量特征 | 等级特征 | |
| 配置符号 填充 |
形状+色彩 方向 |
密度 | 色彩+透明度 +密度+尺寸 |
| 图案填充 | 色彩+形状 方向+形状 |
||
| 渐变填充 | 色彩 | 透明度 | |
| 色彩填充 | 色彩 | 透明度 | |
| 图片填充 | 图案 | 透明度 | |
基本图元在图元布局的约束下进行组合配置来构建统计制图符号,如图 10所示。单一统计符号的构建最简单,这里只讨论关系统计符号和集合统计符号的构建方法。

|
| 图 10 统计制图符号的构建 Fig. 10 Construction of Statistical Graphics Symbol |
1) 关系统计符号的构建
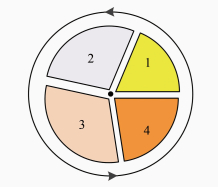
关系统计符号由多个视觉变量或几何图元组合而成,用以表达单个地理要素的多个指标之间的相互关系,图元或视觉变量与单一指标密切关联。关系统计符号中二维饼符号最为典型,它由中心布局约束下的扇形图元构成,扇形图元的个数由布局关联的复合指标中包含的字段个数决定。从布局起始方向开始,围绕中心布局的控制点(圆心),进行逐个图元绘制,图元的角度和半径绘制参数都与专题要素数据密切相关,通过实时计算而来,如图 11所示。
|
| 图 11 饼状图符号的构建方法 Fig. 11 Construction Method of Pie Chart Symbol |
2) 集合统计符号的构建
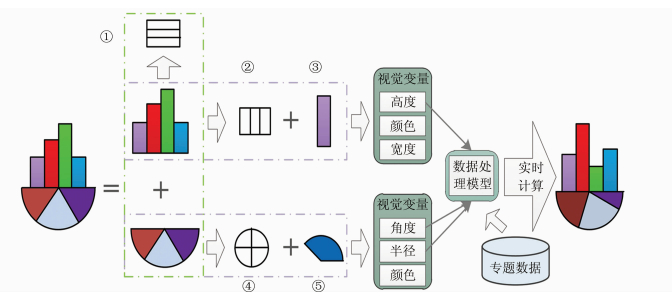
集合统计符号由单一统计符号和关系统计符号叠加组合而成,用以表达多个地理要素中多个指标各自的数据特征,各个符号之间相互独立。基本图元在布局的约束下生成子符号,多个子符号在其上一层布局的约束下组合成更高级的集合统计符号。如图 12所示,最外层是线性布局①,其下层又嵌套了线性布局②和中心布局④。其中,线性布局②包含4个矩形图元③,组合成直方柱子符号;中心布局④包含三个扇形图元⑤,组合成半饼子符号。两个子符号最终在线性布局①的约束下构成集合符号。符号中客观视觉变量的外在形式是通过与其关联的数据处理模型实时计算得到的。
|
| 图 12 集合统计符号的构建方法 Fig. 12 Construction Method of Union Symbol |
以制作反映某地区粮食产量结构和人口数量组成的统计专题地图为例,在设计开发的统计专题图制作模块中验证上述符号构建方法。
图 13为Windows操作系统平台下制作的专题地图,构建了结构饼+直方柱的集合统计符号。

|
| 图 13 某地区粮食产量和人口结构图 Fig. 13 Map of Grain Production and Population Structure in a Given Area |
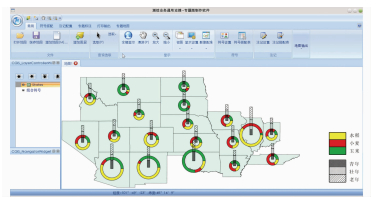
图 14为国产麒麟操作系统平台下制作的多样化显示效果图,实现了相同数据不同平台的不同显示效果,构建了结构环+直方柱的集合统计符号。
|
| 图 14 统计专题地图多样化显示 Fig. 14 Various Show of Statistic Thematic Map |
通过对应用实例的分析可以看出,与其他方法相比,应用此构建方法能够达到以下目的。
1) 突破传统统计制图符号对数据依赖性强且构建复杂的局限,将空间布局的思想引入专题制图领域,增强地图符号对多要素、多指标专题数据的表达能力,体现统计制图符号的数据相关特性。
2) 以“视觉变量→图元→符号”的多层次架构完成统计制图符号的构建,结合其形式化语言描述,实现符号的共享与跨平台移植。
3) 弥补MapInfo、SuperMap等常见GIS软件中符号样式单调,类型缺乏(仅仅是线划符号)的不足,提供设计美观、结构复杂的集合统计制图符号,丰富符号种类。
4 结 语实践证明,利用空间布局构建统计制图符号的方法,能够制作结构复杂、构图精美的地图符号,实现符号共享与跨平台移植,更有利于统计专题图的制作。但是,符号设计知识的复杂性和制图过程中的不确定性,决定了该方法在符号自动构建上的不足。如何将艺术化的地图符号设计工作算法化,真正实现符号的自动化制作,仍有待进一步研究。
| [1] | Wang Hailong. Research on Cartographic Visualization for Statistical Data[D]. Zhengzhou: Information and Engineering University, 2007(王海龙. 统计数据地图可视化研究[D]. 郑州:信息工程大学,2007) |
| [2] | Ma Yaofeng. A Study on the Symbolic Constitution Elements of Thematic Map[J]. Geographical Research, 1997, 16(3): 23-31(马耀峰.专题地图符号构成元素的研究[J]. 地理研究,1997,16(3):23-31) |
| [3] | Ai Tinghua. Dynamic Symbol and Dynamic Map[J].Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 47-51(艾廷华. 动态符号与动态地图[J]. 武汉测绘科技大学学报,1998,23(1):47-51) |
| [4] | Bertin J. Graphics and Graphic Information Processing[M]. Berlin: Walter de Gruyter, 1981 |
| [5] | Mennojan K, Arjen K. A Classification of Cartographic Animations: Towards a Tool for the Design of Dynamic Maps in a GIS Environment[C]. The Seminar on Teaching Animated Cartography, Spain, 1995 |
| [6] | Xu Zhiyong, Ai Tinghua, Wei Yongjun, et al. On Visual Variables of 3D Map Symbol[J]. Geomatics and Information Science of Wuhan University, 2006, 31(6): 557-560(徐智勇,艾廷华, 危拥军,等. 三维地图符号视觉参量研究[J]. 武汉大学学报·信息科学版,2006,31(6):557-560) |
| [7] | Ai Tinghua,Zhu Huang, Wang Hong, et al. Dynamic Electronic Map Design to Monitor Change Phenomena[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 858-861(艾廷华,朱熀, 王洪,等. 面向变化监控的动态电子地图设计[J]. 武汉大学学报·信息科学版,2005,30(10):858-861) |
| [8] | Wei Wenzhan, Zhong Yexun, Huang Rentao, et al. Mathematical Definition on the Visual Variables of the Cartographic Symbols[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5): 511-515(魏文展,钟业勋,黄仁涛,等. 地图符号视觉变量数学定义的研究[J]. 武汉大学学报·信息科学版,2002,27(5):511-515) |
| [9] | Zhang Yi, Cao Yani, Ai Bin, et al. Adaptive Generation of Statistical Map Symbol Based on Visual Elements[J]. Surveying and Mapping, 2012, 35(4): 155-159(张毅,曹亚妮, 艾彬,等. 基于视觉元素的统计地图符号自适应生成[J]. 测绘,2012,35(4):155-159) |
| [10] | Li Wei, Zhou Yongqian. The Design and Implementation of a Symbol Base in Thematic Mapping[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1997, 22(3): 263-265(李伟,周勇前. 专题制图符号库的设计与实现[J]. 武汉测绘科技大学学报,1997,22(3):263-265) |
| [11] | Schnabel O, Hurni L. Primitive-based Construction Theory for Diagrams in Thematic Maps[J]. Cartograhic Journal, 2009, 46(2): 136-145 |
| [12] | Wu Xiaofang, Xu Zhiyong, Cai Zhongliang, et al. Design and Implementation of High Precision Map Symbol Library Based on GDI+[J]. Geomatics and Information Science of Wuhan University, 2004, 29(10): 928-932(吴小芳,徐智勇, 蔡忠亮,等. 基于GDI+的高精度地图符号库的设计与实现[J]. 武汉大学学报·信息科学版,2004,29(10):928-932) |
| [13] | Che Sen, Sun Qun, Liu Haiyan, et al. Design of a Parameter Controlling Symbol Editing Tool[J]. Geomatics and Information Science of Wuhan University, 2013, 38(11): 1 326-1 329(车森,孙群,刘海砚,等. 参数控制的地图符号编辑器设计[J]. 武汉大学学报·信息科学版,2013,38(11):1 326-1 329) |
| [14] | Yin Zhangcai, Li Lin, Zhu Haihong, et al. Description Model of Map Symbols Based on SVG[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 544-547(尹章才,李霖, 朱海红,等. 基于SVG的地图符号描述模型研究[J]. 武汉大学学报·信息科学版,2004,29(6):544-547) |
| [15] | Yan Yulong, Jiang Nan,Cui Huping, et al. Research on Statistical Graphics Symbol Building Model Oriented Fast Making[J]. Journal of Geomatics Science and Technology, 2014, 31(1): 102-106(颜玉龙,江南,崔虎平,等. 面向快速制作的统计制图符号建造模型的研究[J]. 测绘科学技术学报,2014,31(1):102-106) |
| [16] | Kantorovich L V.Mathematical Methods of Organizing and Planning Production [J]. Management Science, 1960, 6(4): 366-422 |
| [17] | Dowsland K A, Dowsland W B. Packing Problems[J]. Europen Journal of Operational Research, 1992, 56(1): 2-14 |
| [18] | Dong Hongyu, Yang Qingming. Space Layout[M]. Nanchang: Jiangxi Fine Arts Publishing Press, 2003(董红羽,杨清明. 空间布局[M]. 南昌:江西美术出版社,2003) |
| [19] | Gao Jun. Map, Cartography Theory Characteristics and Scientific Structure[J].Map, 1986,1: 7-8(高俊.地图、地图制图学理论特点与科学结构[J]. 地图,1986,1:7-8 |
 2015, Vol. 40
2015, Vol. 40


