文章信息
- 王玉着, 刘修国, 张唯
- WANG Yuzhuo, LIU Xiuguo, ZHANG Wei
- 并行化多流向策略的栅格河网提取算法
- Raster River Networks Extraction Based on Parallel Multiple Flow Direction Algorithms
- 武汉大学学报·信息科学版, 2015, 40(12): 1646-1652,1682
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1646-1652,1682
- http://dx.doi.org/10.13203/j.whugis20140645
-
文章历史
- 收稿日期: 2014-09-09

基于DEM进行地形属性值计算和各种特征信息提取的数字信息处理技术被称为数字地形分析(digital terrain analysis,DTA)。地表流 域水系特征提取是DTA的关键技术之一,对水文分析、土壤侵蚀及地理模拟等领域的研究具有重要影响[1, 2, 3]。目前应用较广泛的流域特征提取方法是地表漫流模拟法[4],其水系提取的关键在于确定每个格网单元的汇流累积量。汇流累积量取决于格网单元的流量分配策略,主要有单流向(single flow direction,SFD)和多流向(multiple flow direction,MFD)两类算法。SFD算法认为水流方向为其邻域坡降的最低方向,如D8算法[5]、Rho4/Rho8算法[6]、Lea算法等[7],模型结构简单,应用范围广。但SFD算法模拟水流在坡面上散漫流动时,提取的河网会出现不合理的平行流现象[7]。MFD算法认为水流应向 邻域中所有高程值较低的方向分配,如FD8/FRho8算法[8]、FMFD算法[9]以及MFD-fg("-fg"代表function of gradient)算法[10]等。相比SFD算法,MFD算法能较好地模拟水流在坡面上的散漫流动,且物理意义明确,更符合水流的实际特征。MFD-fg算法充分考虑地形对水流分配的影响,根据当前位置的下坡坡度动态调整水流的分配策略,在自然水流模拟方面取得了较好效果。
但MFD-fg算法沿用了传统的DEM数据预处理方法,通过洼地去除等操作,确保区域河网的连续性,且出水口始终位于区域的边缘。这些预处理会在区域内产生平行河道或伪河道,造成误差。为了解决DEM数据预处理造成的精度误差及无法准确提取河流、湖泊信息等问题,Rueda等[11]提出了基于单流向淹没策略的栅格河网提取算法(简称R&N算法)。R&N算法直接对原始DEM数据提取一定宽度的河网,规避了预处理过程,确保了河网数据的精度。但R&N算法采用SFD策略,容易在原本连续河道地区导致河网断裂,且该算法是串行实现的迭代算法,计算复杂,非常耗时。
随着水文分析研究范围的扩展和精度的提高,对栅格河网提取的效率也有了更高的要求。为实现基于高精度地形快速获取一定宽度河网的目的,本文在保留R&N算法免预处理优势的基础上,借鉴MFD-fg算法的水流分配策略,提出了基于多流向淹没模型的流域河网提取算法,利用GPU(graphics processing unit)技术编程实现,简称P-MFD(parallelizing multiple flow direction )算法。
本文选取湖北省境内的漳河流域、金钱河流域以及郁江流域为三个实验区域,分别采用P-MFD、R&N及D8算法(ArcGIS计算) 对不同分辨率的DEM数据提取河网。结果表明,P-MFD算法提取河网空间形态合理,与现有[5, 6, 7, 8, 9, 10, 11]方法相比,新方法能够快速、高效、准确地提取流域河网。
1 多流向淹没算法提取栅格河网 1.1 多流向算法流域河网算法的核心是确定中心像元的水量分配。本文采用MFD-fg[10]算法允许水流向邻域中所有下坡像元进行分配,可以合理地模拟地形变化对水流分配的影响。MFD-fg算法以最大下坡坡度的线性函数作为水流分配的权值,简化了地形起伏对水流分配的影响。其流量的分配公式为[10]:
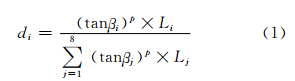
式中,di为中心像元水流对第i号邻域像元的分配比例;tanβi是中心像元对第i号邻域像元的坡度;Li和Lj分别为第i和第j号邻域像元的等高线长度加权因子;第i号邻域像元的等高线长度加权因子[12]定义为:

p表示水流分配权重,代表水流的汇聚程度。当p为0时,在所有下坡邻域单元之间平均分配中心单元的流量;当p趋于无穷大时,即为沿最陡下坡邻域单元流动的单流向分配算法。Freeman[9]通过研究得到,p=1.1时最适合模拟水流完全漫散流动的情况;Quinn[12]等认为p=10时可有效模拟单向流。秦承志[10]等参考前人研究成果,认为p值域为[1.1,10],得到MFD-fg方法的函数形式:

式中,e为最大下坡坡度;emin、emax分别为区域中的最小值和最大值。
1.2 多流向淹没算法河网提取基于MFD-fg和水流传输模型[14]结合的流域河网算法无须对DEM进行预处理。DEM数据中洼地和平地在算法实现过程中通过水量的自然流动补充,精确地提取一定宽度的河网数据。算法实现过程主要包含以下4个步骤。
1) 将DEM数据中所有的像元值初始化为一个常量水量值w,组成水流传输矩阵 DW ,用以模拟自然水量的流动过程。
2) 对DEM数据,通过迭代方式模拟相邻像元之间的水量漫流过程。 中心像元c的高程值为z(c),水量为w(c),高程和水量和为zw(c),遍历DEM数据中的像元,对每个像元 c计算其与邻域8个像元的水量分配系数。水流从像元c按照分配系数将水量w(c)依次流动到满足条件的邻域像元n中,更新n中的汇流累积量值DA(n)及水流传输矩阵 DW (n),同步将水量累加到总流量和中。
3) 重复迭代计算步骤2),直到总流量和等于零或者小于指定的流量阈值DT,则此迭代结束。
4) 遍历汇流累积量DA中的每个像元,将大于指定河网阈值NT的像元提取出来,形成的结果数据即为提取的栅格河网。
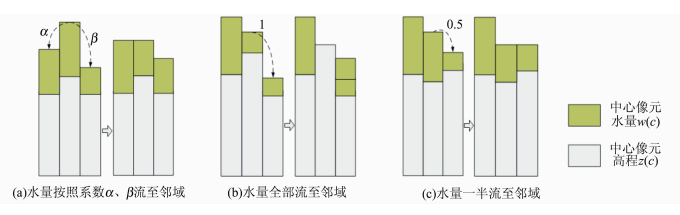
每个像元的水流方向分配系数的确定及水流传输矩阵的计算是算法中的最关键步骤。对于指定像 元c,若该像元为边界像元,则水量w(c)全部流出,w(c)重置为0;否则,对像元c按照式(1)计算3×3邻域内水流的分配比例d(n),若d(n)小于等于0,则该邻域像元n无水量流入,否则对像元n按照式(4)计算流入的水量大小mv(n),如图 1所示,图 1(a)、1(b)、1(c)分别表示在不同情况下水量分配情况。
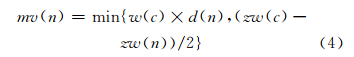
|
| 图 1 像元水流传输矩阵运算前后结果 Fig. 1 The Results Before and After a Water Transfer Matrix Operation |
图 1(a)中,中心像元 c按照式(1)得到满足条件的邻域像元的水量分配系数α和β(α+β=1),将w(c)分别迁移到邻域像元w(n)中,w(n)按照式(4)同步增加不同的水量;图 (1b)中,中心像元c水量w(c)全部迁移到w(n)中,w(n)水量同步增加w(c),同时w(c)重置为0;图 1(c)中,中心像元为洼地,洼地被水量填平后,高程值较低的像元会逐次流出到邻域中,解决洼地和平地的流向。本文算法利用此特性,避免了对DEM数据的预处理。每一次迭代过程中,由于水量w(c)及水流方向的计算因zw(c)不同而不同,计算得到的流量分配系数各异,可产生一定宽度的河网数据。
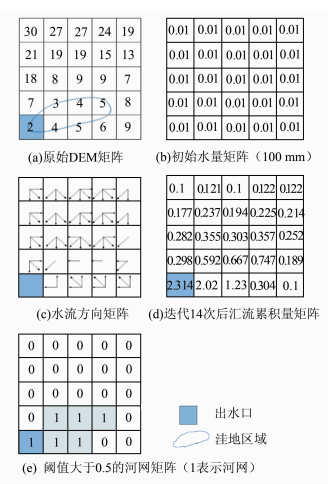
利用此算法对5×5矩阵数据提取河网,提取过程如图 2所示。
|
| 图 2 MFD-fg河网算法生成过程 Fig. 2 The Process of MFD-fg Drainage Net Algorithm |
MFD-fg淹没算法采用串行迭代方式提取栅格河网,其运算时间主要集中在流量分配系数和汇流累积量计算两个方面。本文将GPU与栅格河网提取结合[13, 14],提出基于GPU并行计算的MFD-fg河网提取算法,简称P-MFD,重点对上述两个方面进行基于GPU的并行化处理。
考虑到流量分配系数的计算仅与中心像元及其周边一定范围的邻域像元有关,各像元间的更新相互独立,适合在GPU上并行执行。汇流累积量计算具有较高的空间依赖性,但可以通过水流传输矩阵模型适当减少各像元之间计算的相关性,实现迭代过程的并发执行。
并行算法的实现主要涉及主机端和设备端两个方面[15, 16, 17]。主机端负责在CPU上实现DEM数据常量的水量初始化、内存申请、数据拷贝以及结果河网生成。设备端则完成在GPU的Kernel部分对DEM中每个像元的流量分配系数及汇流累积量计算的迭代模拟。并行策略主要在设备端通过水流传输矩阵模型来实现。在GPU上利用水流传输矩阵对DEM中的每个中心像元和邻域像元的水量分配及汇流累积量进行迭代运算。每次迭代需遍历DEM数据中的所有像元。每个像元在一次迭代循环中水量计算过程可并行化。该像元流出的水量累加至当前一次迭代总流量中,当总流量值小于指定流量阈值时,则此迭代计算过程结束。
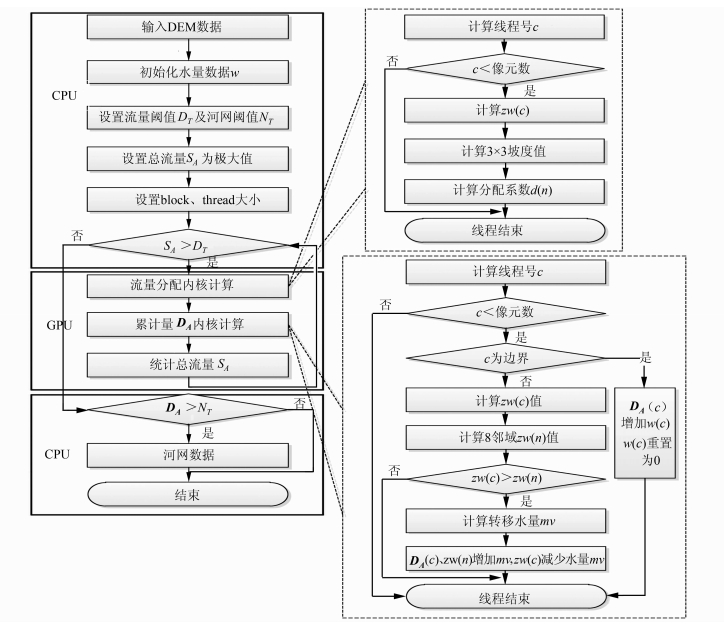
图 3是P-MFD算法流程,其中流量分配系数内核函数及累积量内核函数实现如图 3右侧流程模块所示。具体步骤如下。
|
| 图 3 P-MFD算法流程图 Fig. 3 The Flowchart of P-MFD Algorithm |
1) 初始化水量数据 w,设置流量阈值DT、河网阈值NT及总流量SA(SA初始化为极大值) ;设置合理的线程块(block)、线程thread大小。
2) 根据SA与DT的关系确定迭代是否执行。若SA>DT,则表示当前总流量大于设定流量阈值,则继续迭代;否则,退出迭代,根据河网阈值提取河网。
3) 若满足迭代情况,在GPU上执行流量分配系数及汇流累积量矩阵 DA 内核计算。在每次迭代过程中统计该次计算所得总流量SA。
4) 转到第2)步,继续执行。
5) 迭代结束,判断DA 与NT关系;提取累积量矩阵 DA 中大于河网阈值NT的像元,则得到河网数据。
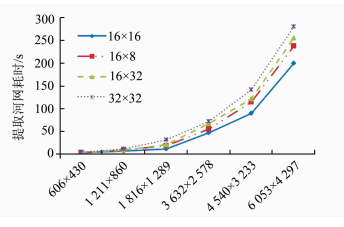
设置block、thread大小和设计设备端执行的并行化指令是提升P-MFD算法执行速度的关键。CUDA架构中,显示芯片的执行最小单元是thread,每个block由多个thread组成,多个block可以构成一个grid。对于GPU为NVIDIA Geforce GTX660的处理器,每个线程块中线程总数应当大于最小线程数128,小于最大线程数1 024。设置不同的block大小,验证采用P-MFD算法提取漳河流域栅格河网所需时间,耗时分布如图 4所示。由图 4可知,在block大小为16×16时,耗时最短,运行速度最快。对于n行、m列的DEM数据,grid按照式(5)计算,其中xthreadsize、ythreadsize为16,分别表示x方向和y方向的线程数,xblocksize、yblocksize为grid中block的个数。
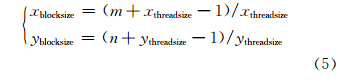
|
| 图 4 设置不同分块调度下提取漳河流域河网耗时 Fig. 4 Execution Time of Extracting Drainage Network Using Different Partitions in Zhanghe |
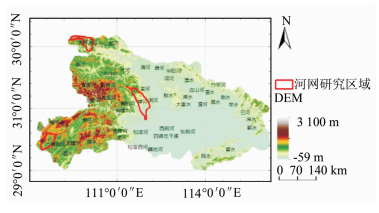
本文选取湖北省境内漳河流域、金钱河流域以及郁江流域为研究区域。漳河流域地处湖北省中部南漳县,总长202 km,海拔37~1 502 m,流域面积约为2 980 km2。金钱河流域位于湖北省西北部郧西县,境内长60.59 km,流域面积971 km2,平均河床比降1.8‰,天然落差110 m,可利用落差90 m。郁江流域在湖北省西南部利川市,全长170 km,海拔205.10~1 790 m,流域面积约为4 602 km2。测试使用的分辨率为30 m的DEM数据由中国科学院国际科学数据服务平台上提供的90 m分辨率数据重采样得到,研究区域如图 5所示。P-MFD算法在Microsoft Visual Studio 2010中利用C++语言设计并实现,其中内核程序利用CUDA完成。算法测试的硬件环境是一台CPU为Intel Core i5-3470(主频3.20 GHz,8 GB内存),GPU为NVIDIA Geforce GTX660(960个处理器,2G显存,显存宽带144.2 GB/s,CUDA 5.5),操作系统为32位Win7的计算机。
|
| 图 5 研究区域的数字高程模型 Fig. 5 DEM of Study Area |
根据§1.2算法描述中w和NT的定义,本文采用初始水量w=100 mm,指定河网阈值NT=15 000 mm,每次迭代过程中,像元的累积总流量大于流量阈值(阈值为初始所有像元流量和的1%),则迭代继续,若小于该阈值,则迭代结束。
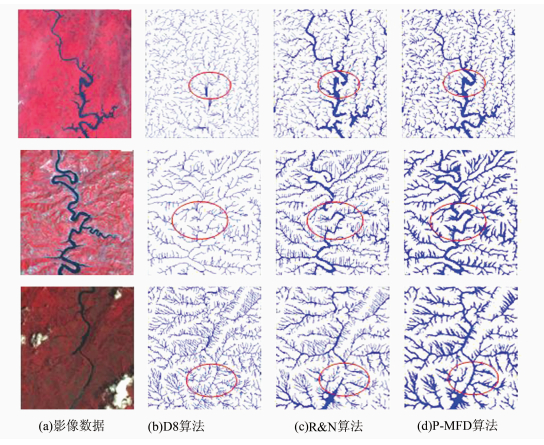
3.2 实验结果及分析 3.2.1 空间形态结果分析为了更加直观地表达算法效果,本文选取漳河流域、金钱河流域及郁江流域中的典型河段作为实验区域,如图 6(a)所示。采用P-MFD、R&N[11]及D8 (ArcGIS计算)三种算法计算各单元网格的汇流累积量并提取栅格河网(河网提取阈值15 000 mm),其结果如图 6(b)、6(c)、6(d)所示(串并行MFD算法提取栅格河网结果相同,图中只选取P-MFD结果)。图 6中3个实验区从上至下依次为漳河、金钱河、郁江。通过分析3种算法的表现可以看出,P-MFD算法与R&N算法提取的河网形态特征一致。两者提取的河网均具有一定宽度,这是由于两者对DEM数据的处理过程相似,不需要对DEM数据预处理,避免了对洼地和平坦区域的处理产生的伪河道及平行河道。但是,从图 6中标记的圆形区域内的河网细节来看,D8算法提取的栅格河网出现了平行流及可能不存在的较小支流; R&N算法由于采用单流向策略导致在原本连续河道地区存在水流方向不连续的情况,其生成的栅格河网也出现断裂现象;P-MFD算法因采用多流向策略,以最大下坡坡度的线性函数对水流进行加权分配,具有较好的水流分配策略,所以其能形成连续且具有一定宽度的栅格河网,其提取的河网数据基本无伪河道及平行河道生成。
|
| 图 6 三种算法提取栅格河网 Fig. 6 Three Algorithms for Extraction Drainage Network |
为了比较不同数据量对处理效率的影响,对实验区域数据重采样以获取不同大小的DEM数据,测试栅格数据大小包括606×430、727×516、908×645、1 211×806、1 816×1 289、3 632×2 578像元数。
采用加速比表示 A算法相对B算法提升的效率:

式中,t1表示A算法运行时间;t2表示B算法运行时间。
表 1列出了4种算法在不同实验区内对不同分辨率数据提取河网的时间消耗(不含输入和输出数据的准备时间)。由表 1可知,同等网格分辨率下,P-MFD算法执行时间最短,串行MFD算法执行时间最长。
| 像元大小 | 漳河流域 | 金钱河流域 | 郁江流域 | |||||||||
| P-MFD | 串行MFD | R&N | D8 | P-MFD | 串行MFD | R&N | D8 | P-MFD | 串行MFD | R&N | D8 | |
| 606×430 | 2.8 | 44.5 | 4.9 | 8.7 | 3 | 53.5 | 3.3 | 9.9 | 1.6 | 29.1 | 1.9 | 7.3 |
| 727×516 | 3.5 | 76.3 | 8.7 | 9.5 | 5 | 94.4 | 9 | 13 | 3.1 | 67.5 | 5.9 | 8.3 |
| 908×645 | 4.6 | 152.1 | 15.3 | 13.1 | 9.5 | 282.6 | 25.3 | 23.2 | 6.4 | 180.9 | 21.7 | 15.9 |
| 1211×860 | 6 | 252.1 | 47.3 | 14.9 | 13.1 | 500.9 | 78.1 | 29.3 | 12 | 471.6 | 86.4 | 25.6 |
| 1 816×1 289 | 11.5 | 550.6 | 109.7 | 22.2 | 20.1 | 880.1 | 280.1 | 48.9 | 29.4 | 1267.5 | 379.2 | 81.8 |
| 3 632×2 578 | 46.5 | 2 448.4 | 698.2 | 89.6 | 89.6 | 4 590.7 | 1 598.7 | 228.3 | 90.5 | 4 446.5 | 1 716.2 | 259 |
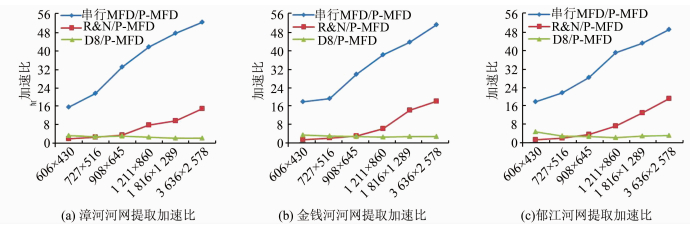
图 7表示P-MFD算法加速比随分辨率增加的变化趋势。由图 7可知,不同实验区域内P-MFD加速比总体趋势一致。并行P-MFD算法相对串行MFD算法在3个研究区域内加速优势显著,加速比最大可达到50倍;相对R&N算法,在金钱河和郁江区域加速比达到1.1~18倍,在漳河区域加速比达到1.7~15倍;相对D8算法其加速比则达到两倍左右。可见,随着数据量的增大,P-MFD算法加速优势更加明显。
|
| 图 7 三个实验区域内P-MFD算法加速比 Fig. 7 Speed-up Ratio of P-MFD in Three Experimental Areas |
本文提出了一种基于并行化多流向策略的栅格河网提取算法。该算法有效规避了传统算法中DEM预处理造成的精度损失,避免生成伪河道及平行河道。同时,采用水流分配策略随下坡坡度变化的多流向(MFD-fg)算法代替传统单流向(SFD)算法,得到连续且具有一定宽度的栅格河网。相比传统算法提取的单像元河网而言,对河流、湖泊、沼泽等水域地貌的表达更为真实。使用并行化策略,有效提升算法的执行效率,充分发挥了在并行计算设备上进行大规模数字地形分析的优势,适应了海量地形数据快速运算的要求。但是,本算法的部分初始参数(初始水量、河网阈值)需要结合地形数据筛选得到,后续将结合全国主要流域数据,研究初始参数与地形的关系,实现初始参数的自动化筛选。
| [1] | Li Jingzhong, Ai Tinghua, Ke Shu. Effective Flow Accumulation Threshold of Extracting Valley-line from Grid-based Digital Elevation Model[J].Geomatics and Information Science of Wuhan University, 2012,37(10):1 244-1 247(李精忠,艾延华,柯舒. DEM提取谷地线的有效汇水量阈值范围[J].武汉大学学报·信息科学版,2012,37(10):1 244-1 247) |
| [2] | Shi Xiaoliang,Yang Zhiyong, Yan Denghua, et al. On Hydrological Response to Land-use/cover Change in Luanhe River Basin[J]. Advances in Water Science, 2014,25(1):21-26(史晓亮,杨志勇,严登华,等.滦河流域土地利用覆被变化的水文响应[J].水科学进展, 2014, 25(1):21-26) |
| [3] | Peng Dongliang, Deng Min, Zhao Binbin. Multi-scale Transformation of River Networks Based on Morphing Technology[J].Journal of Remote Sensing, 2012, 16(5):953-960 |
| [4] | Zuo Junjie, Cai Yongli. An Automated Watershed Delineations Approach for Plain River Network Regions:A Case Study in Shanghai[J]. Advances in Water Science,2011,22(3):337-343(左俊杰,蔡永立.平原河网地区汇水区的划分方法[J].水科学进展, 2011, 22(3):337-343) |
| [5] | O'Callaghan J F, Mark D M.The Extraction of Drainage Networks from Digital Elevation Data[J].Computer Vision, Graphics, and Image Processing, 1984, 28(3):323-344 |
| [6] | Fairfield J, Leymarie P.Drainage Networks from Grid Digital Elevation Models[J].Water Resources Research, 1991, 27(5):709-717 |
| [7] | Lea N L. An Aspect Driven Kinematic Routing Algorithm in Overland Flow:Hydraulics and Erosion Mechanics[M]. NewYork:Chapman &Hall,1992 |
| [8] | Moore I D, Grayson R B,Ladson A R.Digital Terrain Modeling: A Review of Hydrological Geomorphological and Blological Application[J].Hydrological Processes, 1991, 5(1):3-30 |
| [9] | Freeman T G.Calculating Catchment Area with Divergent Flow Based on a Regular Grid[J].Computers & Geosciences, 1991, 17(3):413-422 |
| [10] | Qin Chengzhi, Li Baolin, Zhu Axing,et al. Multiple Flow Direction Algorithm with Flow Partition Scheme Based on Downslope Gradient[J]. Advances in Water Science,2006, 17(4):450-455(秦承志,李宝林,朱阿兴,等.水流分配策略随下坡坡度变化的多流向算法[J].水科学进展, 2006, 17(4):450-455) |
| [11] | Rueda A, Noguera J M, Martinez-cruz C. A Flooding Algorithm for Extracting Drainage Networks from Unprocessed Digital Elevation Models[J].Computers & Geosciences, 2013, 59(10):116-123 |
| [12] | Quinn P, Beven K, Chevalier P, et al. The Prediction of Hillslope Flow Paths for Distributed Hydrological Modeling Using Digital Terrain Models[J]. Hydrological Processes, 1991, 5: 59- 79 |
| [13] | Ortega L, Rueda A.Parallel Drainage Network Computation on CUDA[J].Computers &Geosciences, 2010, 36(2):171-178 |
| [14] | Qin C Z,Zhan L.Parallelizing Flow-accumulation Calculations on Graphics Processing Units—from Iterative DEM Preprocessing Algorithm to Recursive Multiple-flow-direction Algorithm[J].Computers & Geosciences, 2012, 43(6):7-16 |
| [15] | Shao Hua, Jiang Nan, Hu Bin, et al. GPU-based Parallel Bulk Loading R-trees Using STR Method on Fline-Grained Model[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9):1 068-1 073(邵华,江南,胡斌,等. 利用GPU的R树细粒度并行STR方法批量构建[J]. 武汉大学学报·信息科学版, 2014, 39(9):1 068-1 073) |
| [16] | Xiao Han, Zhou Qinglei, Zhang Zuxun. Parallel Algorithm of Harris Corner Detection Based on Multi-GPU[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7):876-881(肖汉,周清雷,张祖勋. 基于多GPU的Harris角点检测并行算法[J]. 武汉大学学报·信息科学版,2012, 37(7):876-881) |
| [17] | Zhang Jianbo, Zhou Sibo,Yuan Guobin, et al. Parallel Processing Mapping Strategy of Spatial Analysis Under the Heterogeneous Environment[J]. Journal of Shanghai Jiao Tong University,2013,47(1):70-75(张剑波,周斯波,袁国斌,等.异构环境下的空间分析并行映射策略[J]. 上海交通大学学报,2013,47(1):70-75) |
 2015, Vol. 40
2015, Vol. 40



