文章信息
- 邓敏, 陈倜, 杨文涛
- DENG Min, CHEN Ti, YANG Wentao
- 融合空间尺度特征的时空序列预测建模方法
- A New Method of Modeling Spatio-temporal Sequence by Considering Spatial Scale Characteristics
- 武汉大学学报·信息科学版, 2015, 40(12): 1625-1632
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1625-1632
- http://dx.doi.org/10.13203/j.whugis20130842
-
文章历史
- 收稿日期: 2015-05-04

时空序列预测分析作为时空数据挖掘中的一个重要技术,主要对在空间上有相互关系的多个时间序列演变趋势与规律进行研究,推测未来时空序列数据的取值或变化趋势。时空序列预测广泛应用于交通控制、气象预报、传染病防治、环境监测等领域。
现有的时空预测建模方法大多是在传统时间序列建模的基础上,结合时空数据的时空自相关特性演变而来的。例如,Martin与Oeppen在ARMA模型的基础上,利用时空延迟算子来表达时空变量在空间与时间上的延迟,提出了时空一体化的STARMA模型[1, 2, 3];程涛等在ANN的基础上采用时空神经元模型来扩展传统的神经网络模型[4];王佳璆等从基于核函数的封闭运算角度构造了适合时空预测STSVR模型的时空核函数[5, 6]。事实上,除了时空自相关性外,时空数据还具有时空尺度依赖特性和时空异质性。其中,时空异质性描述时空变量的统计特征随空间的变化和随时间的演变,是进行时空预测建模的前提条件;而时空尺度特性是指时空数据在不同时间粒度与空间尺度上所遵循的规律与体现的特征不尽相同,利用此性质可以研究时空信息在泛化与细化过程中所反映的特征渐变规律[7]。一般来说,数据在大尺度上体现的全局特征,反映区域性的总变化,受大范围的系统性因素影响;而在小尺度上,局部信息更为突出,受小范围的随机因素影响。在时空序列预测建模过程中,如果忽略了大尺度上的总体趋势,可能导致模型局部过拟合;而如果忽略小尺度的局部变异,则难以捕捉时空数据的细节信息;同时顾及时空数据在这两种尺度上体现出来的变化特征,方可更加全面地综合整体和局部两个层面来对数据中潜在的机理进行挖掘分析。现有预测模型通常忽略了时空数据的尺度特性,仅从单一尺度出发对时空数据进行预测建模。基于此,本文对融合空间尺度特性的时空序列预测模型进行研究,在传统的时间序列预测模型基础上,提出了融合空间尺度特性的时空序列预测建模方法。
1 时空序列数据的尺度特征与空间尺度转换 1.1 时空序列数据的尺度特征尺度是地理空间分析中的一个基本工具,也是空间数据的一个主要属性,是空间分析与管理的主要因素之一[8, 9]。尺度在不同领域中术语与内涵是存在差异的。例如,在地图学中尺度采用制图比例尺进行定义,比例尺是指图上距离与实际距离的比值;在遥感中尺度采用分辨率进行定义,分辨率描述测量的精细程度。本文研究的尺度是通常意义中的空间尺度与时间尺度,也就是指在研究某一物体或过程时采用的空间或者时间单位,同时也可以指某一物体或过程在空间或时间上所涉及的范围。在时空数据挖掘中,空间单位与时间单位常用空间粒度与时间粒度进行表述,而空间范围与时间范围则用空间广度与时间广度进行描述。
地理对象或现象在不同的空间广度与空间粒度下,呈现不同的形式且体现不同的规律。大尺度数据在空间上相对于共同参考的地球表面或其他次级区域,占有较大的空间范围,反映地理对象或现象的整体、抽象、轮廓趋势;而小尺度则占有较小的空间范围,反映地学过程的详细、具体的内容[10]。因此,增加广度,减少粒度,时空数据粗略概括,体现的全局特征愈显著;反之,减小广度,增加粒度,则时空数据细致具体,体现局部信息愈显著。
1.2 时空序列数据的空间尺度转换空间尺度转换是将数据或信息由一个尺度转换到另一个尺度的过程,依据转换的方向分为尺度上推与尺度下推,其中尺度上推是由较小尺度推绎较大尺度的过程,而尺度下推是从较大尺度推绎较小尺度的过程[11, 12]。经典的空间尺度的转换方法主要有:点与多边形的叠加,面域加权,最大化保留以及修正的面域加权等。在时空数据挖掘中,聚类分析技术可将聚类前小粒度的空间单元或对象合并为聚类后较大粒度的空间单元,并且采用统计值来对簇的特征进行描述,因而可采用聚类方法进行空间尺度转换。
时空序列聚类分析依据空间单元在空间域上的邻接性与时间域上的相似性,将时空序列数据划分为不同的簇,使得在满足空间邻接性的条件下,簇内的相似性尽可能大且簇间的相似性尽可能小。时空序列聚类分析不同于传统的空间点聚类。传统空间点实体聚类仅考虑了对象间的空间属性,而时空序列聚类要求对象间在满足空间邻接性的条件下还需度量时间序列的相似性。在已有的研究中,能够对时空序列数据进行聚类的方法主要有:骆剑承等提出的一种多尺度单元区域的划分方法[13],该方法在考虑空间单元的专题属性的同时,顾及空间单元的邻接关系,将空间尺度中小粒度逐渐融合为大粒度,从而得到不同尺度的区域划分;王海起等提出了一种基于空间邻接关系的K-means聚类改进算法[14],该算法在经典的划分聚类K-means基础上,同样考虑空间单元存在的邻接关系,满足邻接关系的对象才划分至同一类中。
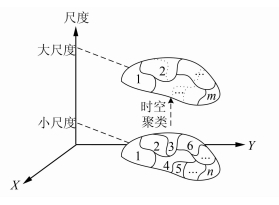
基于聚类分析的尺度上推过程如图 1所示。不妨设小尺度下的时空序列对应 n个空间单元及n个时间序列,对其进行时空序列聚类分析,得到m(m≤n)个簇。属于同一个簇内的若干个空间单元与对应的时间序列分别合并为大尺度下1个对象与对应的1个序列,这样就得到了大尺度下的时空序列(聚类后形成的m个空间单元及m个时间序列),即完成了时空序列由小尺度到大尺度的上推过程。在本文中,小尺度是指时空数据的观测数据尺度,大尺度是借助于聚类有效性评价指标选择最佳聚类结果进行尺度上推得到的数据尺度。
|
| 图 1 基于聚类的尺度转换过程 Fig. 1 Procedure of Scale Transformation Based on Spatial Clustering |
设时空序列在较小空间尺度下表示为:
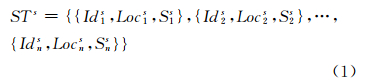
式中,Idis(i=1,2,…,n)表示小尺度下时空序列数据的第i条记录的编号以及对应空间单元的名称;Locis表示小尺度下第i条记录对应空间单元的空间位置;Sis表示小尺度下第i条记录对应空间单元的时间序列。采用§1.2中提出的尺度转换方法,可获取大空间尺度下的时空序列数据:
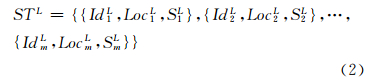
式中,m≤n,IdjL(j=1,2,…,m)、LocjL、SjL分别表示大尺度下时空序列数据第j条记录的编号,即对应空间单元的名称、空间位置和时间序列。由于不同尺度下时空数据体现出不同的规律特征,可知当前小尺度下时空序列由大尺度下反映整体特征的数据与当前小尺度中反映局部特征的数据构成,可表达为:
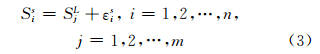
式中,Sis表示小尺度下空间单元Idis所对应的时间序列,经过聚类分析后,Sis及同簇的各时间序列一起合并到大尺度下空间单元IdjL对应的时间序列SjL中,并且SjL表示Idis对应的时间序列在小尺度下的趋势部分;εis表示Idis对应的时间序列在小尺度下的偏差序列:

式中,εiqs(q=1,2,..,t)表示空间单元Idis在小尺度下q时刻的偏差部分。
不难发现,融合空间尺度特性的时空序列预测的基本思路是分别对较大尺度反映的趋势部分以及当前尺度的偏差部分进行预测,一般过程为:首先对时空序列数据进行聚类分析,获取反映当前尺度趋势部分的大尺度数据;然后将当前尺度的趋势部分剔除,剩余部分即为当前尺度数据中反映偏差部分εis。
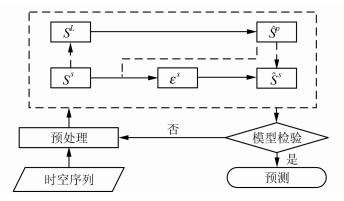
建模过程如图 2所示。原始时空序列数据一般视为小尺度下的数据Ss,通过尺度上推得到大尺度下的时空序列SL。对大尺度下的序列SL进行建模,得到拟合序列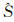 L,
L,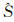 L反映了小尺度下对应各序列Ss的趋势部分;对
L反映了小尺度下对应各序列Ss的趋势部分;对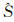 L相对Ss的偏差部分即εs进行建模,修正
L相对Ss的偏差部分即εs进行建模,修正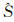 L,即可得到小尺度下各系列的预测模型
L,即可得到小尺度下各系列的预测模型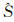 s。通过小尺度下的预测模型得到小尺度下各空间单元的预测值。对小尺度下同一个簇内各单元的预测值进行加权平均,即可获得大尺度下相应空间单元的预测值。
s。通过小尺度下的预测模型得到小尺度下各空间单元的预测值。对小尺度下同一个簇内各单元的预测值进行加权平均,即可获得大尺度下相应空间单元的预测值。
|
| 图 2 融合空间尺度特性预测建模一般性框架 Fig. 2 A General Framework of Prediction Modeling by Considering Spatial Scale |
在对SjL和εis建模时,理论上可以随意选取不同的预测模型,如 ARMA模型、灰色系统模型、神经网络模型、支持向量机模型等。ARMA模型要求时间序列平稳[15],一般情况下难以满足; 灰色系统模型有良好的趋势拟合能力,但是难以提取局部细节;三层的神经网络模型能拟合任意函数,但可能产生过拟合问题;支持向量机模型拟合能力强,但是参数配置复杂,对缺失或异常数据敏感[16]。考 虑到灰色系统模型和神经网络模型的特点分别与SjL和εis的数据特征相匹配,因此用灰色系统模型描述SjL反映大尺度趋势,用神经网络模型描述εis反映小尺度细节信息。
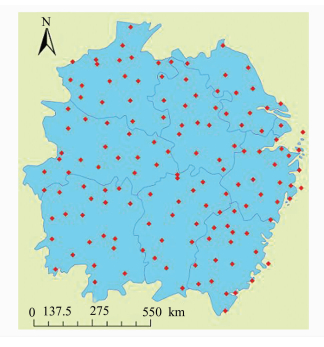
3 实验分析 3.1 降水量预测干旱作为人类面临的主要自然灾害之一,对人类生存、社会发展带来的威胁日益严重。由于所有的干旱事件都源于降水的缺乏,并且降水存在空间异质性,因此准确的降水预测结果对区域抗旱减灾具有重要意义。为此,本实验采用融合空间尺度特性的时空序列预测建模方法对我国局部区域降水进行了预测建模分析。实验数据为我国东部9省市地面降水观测站1950~2011年的降水数据,研究区的地理位置如图 3所示。数据来源于中国气象科学数据共享服务网。经过统计,大部分站点的数据在1961~1990年间比较完整,选取其中141个数据完整的站点进行分析预测。
|
| 图 3 降水量预测研究站点分布 Fig. 3 Distribution of Stations of Precipitation Prediction Research |
首先,对地面观测站点生成Voronoi图,站点所属的多边形(空间单元)与站点观测的降水时间序列一起构成了基本尺度(小尺度)下的时空序列,该时空序列有141条记录,每条记录的编号为各站点的名称,按式(1)格式记录,该尺度下记录的总条数 n=141,如式(5):
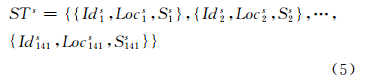
式中,Idis(i=1,2,…,141)表示小尺度下第i个站点的降水观测序列对应的空间单元的编号;Locis为对应空间单元的坐标及隐含的拓扑信息;Sis为对应的降水时间序列。
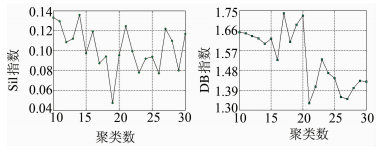
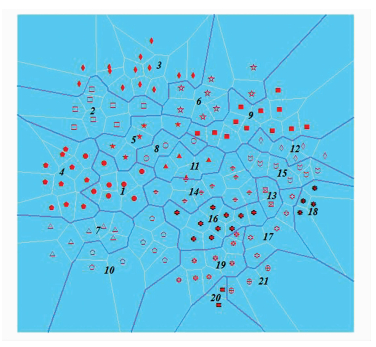
采用§1.2中提到的时空序列聚类分析,为了得到合理的聚类结果,在聚类的过程中调整簇的个数,并计算不同簇个数情形下的聚类可靠性评定指标Sil指数和DB指数。Sil指数计算簇的凝聚度和分离度,DB指数计算簇内紧密性和簇间分离性的比率。Sil指数越大,DB 指数越小,则表示聚类的结果越可靠,计算结果如图 4所示。从图 4中可以看到,簇的个数为21时Sil指数取得极大值,而DB指数取得最小值,因此认为簇的个数为21时聚类结果比较可靠,聚类结果如图 5所示。根据聚类结果对时空序列进行尺度上推可以得到大尺度下的时空序列:
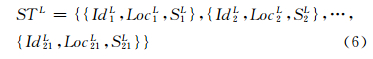
式中 ,时间序列SjL(j=1,2,…,18)是由记录IdjL对应的小尺度下各时间序列加权平均得到,权值为小尺度下各空间单元的面积与对应的空间单元IdjL的面积的比值。由于要计算空间单元的面积,选择所有空间单元都完整且无变形的簇进行分析,此处只选取编号为1、5、8、11、13、14和16这7个大尺度空间单元的时空序列数据。
|
| 图 4 聚类结果可靠性评价 Fig. 4 Validity Evaluation of Clustering of Spatio-temporal Series |
|
| 图 5 降水量时空序列聚类结果 Fig. 5 Clusters Results of Spatio-temporal Series of Precipitation |
根据§2的描述,首先对大尺度下的时间序列进行建模,即运用灰色理论对SjL建立GM(1,1)模型以提取小尺度下各个空间单元的发展趋势,然后采用BP神经网络(BPNN)模型对小尺度下各空间单元的局部偏差部分εis部分进行建模,因此小尺度下预测模型可以表示为:
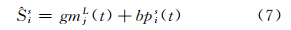
式中,gmjL(t)表示建立的GM(1,1)模型;bpis(t)表示建立的BPNN模型。其中,IdjL取值1、5、8、11、13、14和16时,Idis表示与这7个大尺度空间单元对应的小尺度单元的编号(用各站点的地名表示),IdjL和Idis的对应关系列于表 1。
| IdjL | Idis |
| 1 | 宜昌、荆州、南县、嘉鱼、岳阳、常德、沅江、平江 |
| 5 | 信阳、钟祥、广水、天门、固始 |
| 8 | 麻城、武汉、霍山 |
| 11 | 英山、黄石、安庆、九江 |
| 13 | 金华、丽水 |
| 14 | 修水、黄山、庐山、波阳、景德镇、屯溪、南昌、衢州、玉山 |
| 16 | 樟树、贵溪、龙泉、南城、邵武、七仙山、浦城、建阳、广昌、泰宁 |
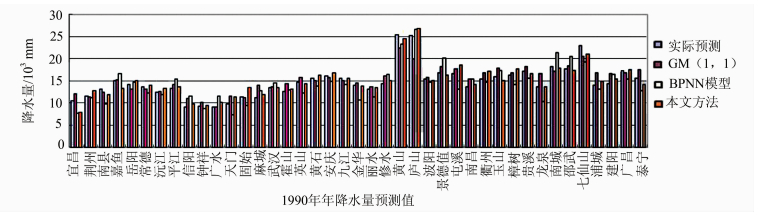
采用本文方法对表 1中小尺度下各站点的1961~1989年的降雨时间序列进行建模,预测1990年的降水值,并与BP神经网络模型以及GM(1,1)模型的预测结果进行比较,如图 6所示。整体来看,本文的方法比其他两种方法的预测值都要更接近真实值。但是,也有些站点的预测情况不是很理想,其原因主要有两点:一是因为降水量时序数据的自相关性不是很强,即前面几期的数据对后面一期或几期的数据影响不够强,导致预测的准确度不高;二是因为样本不够完备,30期年降水数据是一个很小的样本,往往无法映射出将来会出现的一些异常情值。因此,对于一些极端异常情况,通过时序数据预测是很困难的。但是即使在这种极端的情况下,本文的预测方法相比于其他两个方法仍具有一定的优越性。
|
| 图 6 小尺度下各空间单元1990年降水量预测值 Fig. 6 Prediction of Annual Precipitation of Each Spatial Unit in 1990 at Small Scale |
进一步采用相对平方误差(RSE)、正态均方误差(NMSE)、均方根误差(RMSE)和绝对误差(MAE)对本文方法的预测性能进行全面定量评估,各指标的计算结果列于表 2。从表 2可以发现,本文方法的各种指标都显著低于另两种方法,从而验证了本文方法良好的预测性能。
| 模型 | RSE | NMSE | RMSE | MAE |
| GM(1,1)模型 | 0.208 3 | 0.012 1 | 1 647.98 | 1 287.31 |
| BPNN模型 | 0.346 6 | 0.021 4 | 2 126.13 | 1 907.85 |
| 本文方法 | 0.086 9 | 0.005 1 | 1 064.57 | 854.09 |
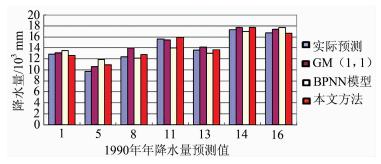
进而对大尺度下的时空序列进行预测和评价。如§1所述,依据小尺度下每个空间单元1990年的降水量预测值,用加权平均的方法计算 大尺度下编号为1、5、8、11、13、14和16的空间单元的1990年降水量预测值,计算结果如图 7所示。其中,大尺度实际观测是由小尺度下各单元实际观测量值加权求得的。从图 7中可以看到,利用本文方法求得的大尺度下的各空间单元1990年年降水量预测值与实际观测值更吻合,因此,本文方法对大尺度下的空间单元也能取得良好的预测结果。
|
| 图 7 大尺度下各空间单元1990年降水量预测值 Fig. 7 Prediction of Annual Precipitation of Each Spatial Unit in 1990 at Large Scale |
最后,分别对三种方法在大尺度下的预测结果进行定量评价,计算结果列于表 3。本文方法预测值的各项指标较其他两种方法均大幅度下降,这说明本文方法在大尺度下也能取得较好的预测结果。
| 模型 | RSE | NMSE | RMSE | MAE |
| GM(1,1)模型 | 0.100 7 | 0.003 0 | 789.23 | 635.81 |
| BPNN模型 | 0.207 0 | 0.006 4 | 1 131.25 | 919.48 |
| 本文方法 | 0.042 2 | 0.001 3 | 510.98 | 370.20 |
大气污染研究是人类健康研究领域的一个重要方向,大量的研究表明,短时间暴露在严重的空气污染中会导致急性健康问题,比如眼睛发炎、呼吸困难、肺部以及心血管不适等;而长时间暴露 在严重的空气污染之中会导致癌症,免疫系统、神经系统、生殖系统和呼吸系统疾病。对大气污染时空序列进行建模,准确预测大气污染物浓度变化趋势,对居民合理选择日常活动范围,合理规划出行路线,降低大气污染引起的身体不适等有着重要意义。本实验以北京市日平均PM2.5浓度时空序列进行建模分析,实验数据来自北京市35个地面空气质量观测站,站 点空间分布如图 8所示。数据的时间跨度为2014年4月1日~2014年5月31日,共61期数据,利用前面60期数据建模,预测第61期数据,并与观测值进行交叉验证。

|
| 图 8 PM2.5浓度预测研究站点分布 Fig. 8 Distribution of Stations of PM2.5 Concentration Prediction Research |
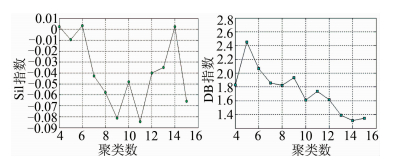
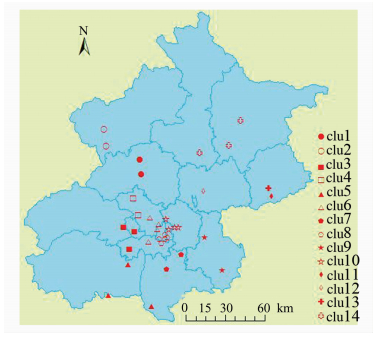
根据§2的描述对PM2.5时空序列进行建模,建模具体过程与§3.1描述相同。首先通过聚类对小尺度的PM2.5时空序列数据进行尺度上推,调整聚类过程中所得簇的数目,计算Sil指数和DB指数,如图 9所示。从图 9中可以看出,簇的数目为14时Sil指数取到极大值而DB指数取到最小值,因而此时聚类结果比较可靠。聚类结果如图 10所示,图例中clu1~clu14表示簇的编号。
|
| 图 9 PM2.5浓度时空序列聚类可靠性评价结果 Fig. 9 Validity Evaluation of Clustering of Spatio-temporal Series of PM2.5 Concentration |
|
| 图 10 0 PM2.5浓度时空序列聚类结果 Fig. 10 Clusters Results of Spatio-temporal Series of PM2.5 Concentration |
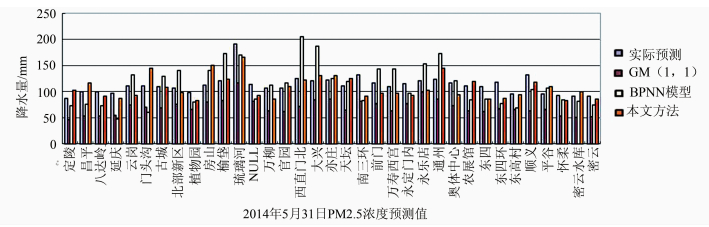
用GM(1,1)模型对大尺度下PM2.5浓度序列建模,提取小尺度下各个空间单元的趋势部分,然后用BP神经网络模型对小尺度下各空间 单元的局部偏差部分建模,趋势部分的预测结果和偏差部分预测结果耦合即为小尺度下各空间单元PM2.5的预测值,小尺度下的预测结果如图 11所示。从图 11可以看出,GM(1,1)模型的预测结果普遍低于观测值,而BPNN模型的预测结果不稳定,个别预测值和观测值相差很大。其原因在于,5月31日的PM2.5浓度较前几天有大幅度的跳跃,GM(1,1)模型能有效拟合整体趋势,对局部细节变化的预测能力较弱,而BPNN模型预测存在过拟合问题,导致某些结果的误差很大。进一步采用精度评估指标全面评估预测结果,计算结果列于表 4。可以看到,本文方法的各项指标都显著低于其他两个方法。
|
| 图 11 小尺度下各站点PM2.5日均浓度预测值 Fig. 11 Evaluation of PM2.5 Concentration Prediction at Small Scale |
| 模型 | RSE | NMSE | RMSE | MAE |
| GM(1,1)模型 | 5.922 5 | 0.237 8 | 43.17 | 41.96 |
| BPNN模型 | 3.425 1 | 0.085 9 | 32.83 | 27.55 |
| 本文方法 | 1.084 2 | 0.028 4 | 18.47 | 15.53 |
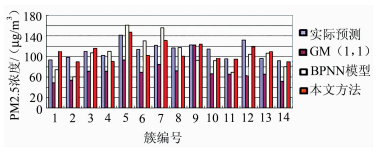
同样地,对大尺度下的时空序列进行预测和评价,依据小尺度下每个空间单元PM2.5浓度预测值分别求出14个簇内站点预测值的平均值,把平均值作为大尺度下的预测值,结果如图 12所示。其中,大尺度下实际观测 量值是小尺度下各站点的实际观测量值的平均值,计算各种精度评估指标,结果列于表 5。可以看出,大尺度下,本文方法的预测结果精度也明显高于其他两种方法。
|
| 图 12 大尺度下各站点PM2.5浓度预测值 Fig. 12 Prediction of PM2.5 Concentration at Each Station at Large Scale |
| 模型 | RSE | NMSE | RMSE | MAE |
| GM(1,1)模型 | 8.349 2 | 0.235 9 | 42.47 | 41.26 |
| BPNN模型 | 4.783 9 | 0.078 9 | 32.15 | 28.67 |
| 本文方法 | 0.548 5 | 0.009 9 | 10.89 | 9.43 |
本文提出了一种融合空间尺度特性的时空序列预测建模方法,该方法主要考虑到空间数据在大空间尺度上体现全局特征,在小空间尺度上局部特征更为突出的特点。因此,针对趋势与偏差部分体现出来的数据特征,分别采用不同的模型进行预测,并通过对实际的降水数据和PM2.5浓度数据进行建模分析,进一步验证了本文方法能用于两个空间尺度预测,在预测精度上亦优于不考虑空间尺度特性的预测方法。
本文方法亦存在一定的局限性,未来需要在以下三个方面进一步开展深入研究:(1)本文采用时空序列聚类方法进行由小尺度到大尺度的尺度转换,不同的聚类方法以及同一方法中参数取不同的值可能导致不同的尺度转换结果,如何选取合理的聚类方法进行预测,以及聚类结果对预测精度的影响如何,是需要进一步研究的问题;(2)尺度作为时空数据基本特征,难以直接对其进行定量分析,因而需要从理论上给出严密的数学证明,而不仅仅是本文侧重的实例验证分析;(3)本文只在两个尺度上给出了预测结果,主要是考虑到实际应用中的必要性;但另一方面,亦要考虑聚类过程中数据的可聚性,即尺度上推到什么尺度就失去意义。
| [1] | Martin R L,Oeppen J E. The Identification of Regional Forecasting Models Using Space: Time Correlation Functions[J]. Transactions of the Institute of British Geographers, 1975, 66: 95-118 |
| [2] | Cliff A D,Ord J K. Space-time Modeling with an Application to Regional Forecasting[J]. Transactions of the Institute of British Geographers, 1975, 64: 119-128 |
| [3] | Kamarianakis Y, Prastacos P. Space-time Modeling of Traffic Flow [J]. Computers & Geosciences, 2005, 31(2): 119-133 |
| [4] | Cheng T, Wang J Q, Li X. Space-time Series Modeling by Artificial Neural Network[C]. International Conference on Earth Observation Data Processing and Analysis (ICEODPA), Wuhan,China, 2008 |
| [5] | Wang J, Cheng T, Haworth J. Space-time Kernels[J]. International Archives of the Photogrammetry, 2010, 38: 57-62 |
| [6] | Wang Jiaqiu, Deng Min, Cheng Tao, et al. Spatio-temporal Series Data Analysis and Modeling[M]. Beijing: Science Press, 2012(王佳璆, 邓敏, 程涛, 等. 时空序列数据分析和建模[M]. 北京: 科学出版社, 2012) |
| [7] | Pei Tao, Zhou Chenghu, Luo Jiancheng, et al. Review on the Proceeding of Spatial Data Mining Research[J]. Journal of Image and Graphics, 2001, 6(9): 854-870(裴韬, 周成虎, 骆剑承, 等. 空间数据知识发现研究进展评述[J]. 中国图像图形学报, 2001, 6(9): 854-870) |
| [8] | Li Lin, Ying Shen. Fundamental Problem on Spatial Scale[J]. Geomatics and Information Science of Wuhan University, 2005, 30(3): 199-203(李霖, 应申. 空间尺度基础性问题研究[J]. 武汉大学学报·信息科学版, 2005, 30(3): 199-203) |
| [9] | Turner M G, O'Neill R V, Gardner R H, et al. Effects of Changing Spatial Scale on the Analysis of Landscape Pattern[J]. Landscape Ecology, 1989, 3(3-4): 153-162 |
| [10] | Liu Kai, Wu Hehai, Ai Tinghua, et al. Three-tiered Concept of Scale of Geographical Information and Its Transformation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1 178-1 181(刘凯, 毋河海, 艾廷华, 等. 地理信息尺度的三重概念及其变换[J]. 武汉大学学报·信息科学版, 2008, 33(11): 1 178-1 181) |
| [11] | Hu Yunfeng, Xu Zhiying, Liu Yue, et al. A Review of the Scaling Issues of Geospatial Data[J]. Advances in Earth Science, 2013, 28(3): 297-304(胡云锋, 徐芝英, 刘越, 等. 地理空间数据的尺度转换[J]. 地球科学进展, 2013, 28(3): 297-304) |
| [12] | Meng Bin, Wang Jinfeng. A Review on the Methodology of Scaling with Geo-data[J]. Acta Geographica Sinica, 2005, 60(2): 277-288(孟斌, 王劲峰. 地理数据尺度转换方法研究进展[J]. 地理学报, 2005, 60(2): 277-288) |
| [13] | Luo Jiancheng, Zhou Chenghu, Liang Yi, et al. Scale-space Theory Based Regionalization for Spatial Cells[J]. Acta Geographica Sinica, 2002, 57(2): 167-173(骆剑承, 周成虎, 梁怡, 等. 多尺度空间单元区域划分方法[J]. 地理学报, 2002, 57(2): 167-173) |
| [14] | Wang Haiqi, Wang Jinfeng. A K-means Adapted Algorithm Based Spatial Contiguity Relations[J]. Computer Engineering, 2006, 32(31): 50-51(王海起, 王劲峰. 一种基于空间邻接关系的k-means聚类改进算法[J]. 计算机工程, 2006, 32(21): 50-51) |
| [15] | Wei Erhu, Li Zhiqiang, Gong Guangyu. et al. Fitting Prediction of Pole Motion Time Series Model[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1 420-1 424(魏二虎, 李智强, 龚光裕, 等. 极移时间序列模型的拟合与预测[J]. 武汉大学学报·信息科学版, 2013, 38(12): 1 420-1 424) |
| [16] | Peng Ling, Niu Ruiqing, Zhao Yannan. et al. Prediction of Landslide Displacement Based on KPCA and PSO-SRR[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2): 148-152(彭令, 牛瑞卿, 赵艳南, 等. 基于核主成分分析和粒子群优化支持向量机的滑坡位移预测[J]. 武汉大学学报·信息科学版, 2013, 38(2): 148-152) |
 2015, Vol. 40
2015, Vol. 40


