文章信息
- 徐秋辉, 佘江峰, 宋晓群, 肖鹏峰
- XU Qiuhui, SHE Jiangfeng, SONG Xiaoqun, XIAO Pengfeng
- 利用改进的DCCD和SIFT描述符的影像匹配方法
- An Image Matching Method Based on Improved DCCD and SIFT Descriptor
- 武汉大学学报·信息科学版, 2015, 40(12): 1613-1617,1645
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1613-1617,1645
- http://dx.doi.org/10.13203/j.whugis20130753
-
文章历史
- 收稿日期: 2014-06-28

2. 江苏省国土资源信息中心, 江苏 南京, 210000
2 The Information Center of Land Resources of Jiangsu Province, Nanjing 210000, China
随着无人机影像的研究日益增多,影像匹配在无人机影像接中的应用也越来越广泛。影像匹配[1]是寻找影像之间同名目标的过程,目前主要可分为基于灰度的匹配和基于特征的匹配。由于无人机遥感平台的不稳定性,相邻影像之间的旋偏角和比例尺差异往往较大,采用基于灰度的匹配难以获得令人满意的结果,因此一般采用基于特征的匹配[2]。
基于特征的匹配分为特征提取和特征匹配。特征提取[3]又分为特征检测和特征描述,特征检测是确定特征的位置及主方向,特征描述则是为这些特征建立对各种变化因素保持不变的描述符。
SIFT[4, 5](scale invariant feature transform)算法可用于基于特征的影像匹配。该算法在特征检测阶段首先采用DoG(difference of gaussian)算子搜索影像尺度空间上的局部三维极值点,确定特征点的位置和特征尺度,然后通过拟合三维空间的二次函数进行位置和特征尺度的精确定位,最后去除低对比度的特征点和不稳定的边缘响应点。在特征点描述阶段采用SIFT描述符对特征点进行描述,SIFT描述符不仅具有旋转不 变性,同时还对光照变化具有一定的鲁棒性[6]。
然而,由于生成尺度影像涉及高斯滤波,去除低对比度特征点和不稳定边缘响应点涉及到尺度影像的一阶微分和二阶微分操作[5],使得SIFT算法在特征点检测阶段耗时较长,无法满足快速匹配的要求。
Azad等[7]和陈梦婷等[8]提出了基于Harris角点和SIFT描述符的影像匹配方法,该方法以Harris算子[9]提取的角点作为特征点,采用SIFT描述符描述特征点,并分别采用BBF(best bin first)算法[10]和随机取样一致性(RANSAC)算法[11]进行特征点粗匹配和误匹配特征点剔除。相比SIFT算法,该方法在很大程度上提高了特征点的检测速度,同时又保留了SIFT描述符的旋转和光照不变性,因此取得了良好的匹配效果。
由于Harris角点检测涉及影像的一阶微分和高斯滤波[9],使得角点的检测耗时较长,这在一定程度上影响了上述方法的匹配速度。同时,Noble[12]指出,Harris算子只有在检测“L”类型角点时最优,这一局限也使得上述方法的匹配准确率受到了一定程度的影响。
Smith等[13]提出了可以快速检测角点且在角点定位和抗噪声性方面都优于Harris算子的SUSAN(smallest univalue segment assimilating nucleus)检测器。SUSAN[11]检测器是基于模板的角点检测器,它的基本原理为:在以图像某像元为中心的圆形模板内,如果某区域内每一像元亮度值与该像元亮度值相同或相似,则将该区域称为该像元的“USAN”;计算每一像元的“USAN”,由于位于角点上的像元“USAN”最小,因此寻找最小的“USAN”即可确定角点。
基于SUSAN检测器的原理,Lan等[13]提出了在检测速度和漏检率方面都优于SUSAN检测器的DCCD(double-circle-based corner detector)。DCCD检测出的角点不仅具有强抗噪声性,而且对光照变化和旋转变化具有不变性[14]。
基于此,本文提出一种基于改进的DCCD和SIFT描述符的影像匹配方法。在特征点检测阶段,首先采用改进的DCCD快速提取影像上的关键点,要求这些关键点对图像噪声、光照变化、旋转变化具有不变性;然后确定关键点的主方向,生 成特征点。在特征点描述阶段,采用SIFT描述符对特征点进行描述。在特征点匹配阶段,分别采用BBF算法和RANSAC算法进行特征点粗匹配和误匹配特征点剔除。实验结果表明,与基于Harris角点和SIFT描述符的匹 配方法相比,本文的匹配方法在匹配速度和准确率方面均有提高。
1 特征点检测由于相邻无人机影像之间的比例尺差异较大,为了使特征匹配保持对尺度变化的适应性,同时避免SIFT算法中耗时的尺度空间分析,根据Azad等[7]的建议,分别以(Δs)0、(Δs)1、(Δs)2为尺度,通过双线性插值的方式,为比例尺较大的无人机影像生成三级尺度影像,用于特征点的检测,其中,Δs的值取0.75。
1.1 改进的DCCD检测角点 1.1.1 角点粗检测为了更快速地检测角点,在利用DCCD进行角点检测之前,首先利用MIC(minimum intensity change)算子[15]进行粗检测,初步确定候选角点。
MIC算子检测候选角点的具体过程为用3×3的窗口逐像元检测,并将角点响应函数定义为:
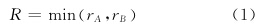
式中,

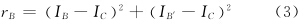
式中,IA、IA′、IC、IB、IB′为各像元的灰度值,定义如图 1所示。

|
| 图 1 参数定义 Fig. 1 Definition of Parameters |
如果某像元的 R值大于某一阈值T1,利用式(4)~(6)分别计算C、B、A的值


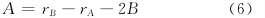
式中,

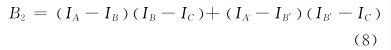
如果B < 0,且A+B>0,则将角点响应函数定义为:
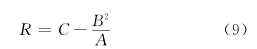
如果像元的R值大于某一阈值T2,则以该像元为中心,在其3×3的邻域内进行非最大值抑制,即判断该像元的R值在其邻域内是否为最大。如果是,则视该像元为候选角点。
1.1.2 DCCD检测角点DCCD[14]采用双圆环作为模板,与大多数基于模板的角点检测器采用圆形、正方形或者菱形作为模板相比,可以避免信息冗余,提高角点的检测速度;同时,DCCD检测出的角点不仅具有强抗噪声性,而且还对光照变化和旋转变化保持不变,因此本文采用DCCD检测角点。
DCCD检测角点的具体过程为:以待检测像元 O为中心,r0=3、r1=5建立双圆环模板,如图 2所示。图 2中,C0为内圆环,C1为外圆环。

|
| 图 2 双圆环模板 Fig. 2 Template of Double Ring |
利用式(10)分别计算 C0的灰度方差Var0和C1的灰度方差Var1:
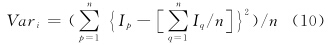
式中,n为圆环上的像元数量,i=0时,n=8,i=1时,n=20;Ip和Iq分别为圆环上像元p、q的灰度值。
将像元O与C0上的每一个像元进行灰度比较,若满足

则认为该像元与像元O相似。通过这样的比较,统计C0和C1上与像元O相似像元的数量,分别记作N0和N1,并将角点响应函数定义为:

如果N0≤4且N1≤9,则以像元O为中心,在其9×9的邻域内进行非最小值抑制,即判断该像元O的R值在其邻域内是否为最小,如果是,则视像元O为角点,并提取该角点为稳定关键点。
1.2 确定关键点主方向为了确定关键点的主方向[5],首先计算影像I(x,y)的梯度值m(x,y)和梯度方向θ(x,y):


然后,由关键点8×8邻域的梯度方向生成梯度方向直方图。该直方图将360°以10°为间隔分成36个区间,将邻域高斯加权后的梯度值在方向区间上进行累加,得到梯度直方图。
最后,寻找关键点邻域的梯度方向直方图的极值用于确定关键点主方向,同时,大于80%极大值的局部极值也用于确定关键点主方向,也就是说,在同一位置和同一尺度上的关键点可以有不同的主方向;由于极值处在方向区间,为了精确确定关键点的主方向,通过二次抛物线方程拟合上述极值附近的三个直方图,确定极值方向,从而确定关键点主方向。
2 特征点描述与匹配 2.1 特征点描述SIFT描述符的构造过程如下[5]。
1) 为了使SIFT 描述符具有旋转不变性,将特征点16×16邻域的坐标横轴旋转至特征点主方向,同时也使该邻域的坐标和梯度方向旋转同样的角度;
2) 对该邻域的梯度值进行高斯加权处理,其中高斯加权核的大小是该邻域宽度大小的一半;
3) 将该邻域分成4×4子区域,在4×4区域内,将360°平均分成8个方向,根据区域的梯度方向,将区域高斯加权后的梯度值分配到这8个方向上,最后生成种子点;
4) 由4×4个种子点生成最佳SIFT描述符,即最佳SIFT描述符应具有4×4×8=128维特征向量。
为了消除光照变化对特征向量的影响,需要对特征向量作标准化处理。针对线性的光照变化,将特征向量标准化为单位长度;针对非线性光照变化,先设置阈值,使单位特征向量的值不超过0.2,然后再将特征向量标准化为单位长度。
2.2 特征点匹配构造特征描述符以后,使用BBF算法[10]进行特征点粗匹配。BBF能够以很高的概率找到待匹配点的最近邻点和次近邻点。如果待匹配点和最近邻点的距离与待匹配点和次近邻点的距离之比小于某一阈值,则认为该最近邻点为待匹配点的候选匹配点。其中,两点之间的距离指的是欧氏距离,若设特征点p、q的特征向量分别为 Desp、 Desq,则特征点p、q之间的欧氏距离d为:
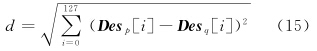
式中,Desp[i]、 Desq[i]分别表示特征点p、q的第 i 维特征向量。
对于粗匹配点对中的误匹配点对,采用RANSAC算法[11]予以剔除:随机选取一定数量的匹配点对,建立仿射变换模型,再随机选取其他匹配点对,由上述仿射变换模型计算其待匹配点的理论匹配点,若实际匹配点与理论匹配点之间的位置误差小于5个像素,则认为该匹配点对为内点对;重复上述运算,直至满足设定的迭代次数,最终获得拥有最大内点对集的精匹配点对。
3 实验结果与分析采用4组相邻无人机遥感影像作为实验数据,影像大小为2 840像素×2 280 像素,空间分辨率为0.2 m。
在特征点检测阶段,先采用改进的DCCD提取关键点,其中T1值取80,T2值取450;再确定关键点主方向,生成特征点。图 3是第1组相邻影像的特征点检测结果。

|
| 图 3 特征点检测结果 Fig. 3 Results of Feature Points Detection |
在特征点匹配阶段,先采用BBF算法粗匹配特征点,再采用RANSAC算法剔除误匹配特征点。其中,BBF算法中最近邻和次近邻距离比的阈值取0.8(Lowe[5]指出当取值0.8时,可以剔除90%的误匹配而仅仅丢失不到5%的正确匹配)。图 4是第1组相邻影像的特征点匹配结果。

|
| 图 4 特征点匹配结果 Fig. 4 Matching Results of Feature Points |
对于匹配结果的精度评价,采用的方法是:用最小二乘法拟合匹配点之间的仿射变换关系,设匹配点对为 P1和P2,将点P1坐标代入上述仿射变换关系,计算P1匹配点理论上对应的位置点P′1,若点P′ 1位置与点P2位置的偏差大于某一容差像素,则认为P2是P1的伪匹配点。本文中,容差像素设为1个像素。
对于T1的值,若设置过小,待匹配点数会增加,匹配耗时也会相对增加;若设置过大,匹配结果的准确率会受到影响。图 5是伪匹配率随T1值变化的曲线,由图 5可以看出,当T1的值取80时,可以获得最低的伪匹配率。

|
| 图 5 伪匹配率随T1值变化的曲线 Fig. 5 False Match Rate with Different T1 Value |
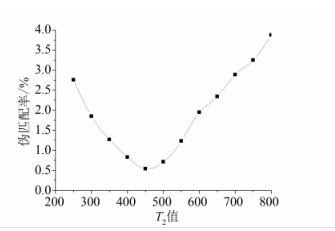
同样,对于T2,若设置过小,待匹配点数会增加,匹配耗时也会相对增加;若设置过大,匹配结果的准确率则会受到影响。图 6是伪匹配率随T2值变化的曲线,由图 6可以看出,当T2取值450时,可以获得最低的伪匹配率。
|
| 图 6 伪匹配率随T2值变化的曲线 Fig. 6 False Match Rate with Different T2 Value |
表 1为本文匹配方法与基于Harris角点和SIFT描述符的快速匹配方法在匹配速度方面的比较。从表 1中可以看出,相比基于Harris角点和SIFT描述符的匹配方法,本文匹配方法的匹配速度提高了4.66~4.78 s。
| 本文匹配方法 | 基于Harris角点和SIFT描述符的匹配方法 | ||||
| 特征点检测耗时/s | 特征点匹配耗时/s | 总耗时/s | 特征点检测耗时/s | 特征点匹配耗时/s | 总耗时/s |
| 8.27 | 8.57 | 16.84 | 11.53 | 10.03 | 21.56 |
| 9.41 | 8.94 | 18.35 | 12.75 | 10.36 | 23.11 |
| 8.89 | 8.77 | 17.66 | 12.14 | 10.18 | 22.32 |
| 10.12 | 9.35 | 19.47 | 13.58 | 10.67 | 24.25 |
表 2为本文匹配方法与基于Harris角点和SIFT描述符的匹配方法在匹配准确率方面的比较。从表 2中可以看出,在匹配准确率方面,本文匹配方法比基于Harris角点和SIFT描述符的匹配方法提高了3.18%~3.49%。
| 本文匹配方法 | 基于Harris角点和SIFT描述符的匹配方法 | ||||
| 伪匹配数 | 匹配总数 | 伪匹配率/% | 伪匹配数 | 匹配总数 | 伪匹配率/% |
| 12 | 2 214 | 0.54 | 81 | 2 163 | 3.74 |
| 21 | 2 642 | 0.79 | 107 | 2 574 | 4.16 |
| 17 | 2 417 | 0.7 | 93 | 2 395 | 3.88 |
| 26 | 2 853 | 0.91 | 124 | 2 816 | 4.4 |
本文提出了一种基于改进的DCCD和SIFT描述符的影像匹配方法。实验结果表明,相对于基于Harris角点和SIFT描述符的匹配方法,本文方法不仅匹配速度提高了4.66~4.78 s,匹配准确率也提高了3.18%~3.49%。但是,无论是本文方法,还是基于Harris角点和SIFT描述符的匹配方法,特征点提取过程中都没有考虑仿射不变性,如何使提取的特征点克服仿射变化的影响是需要进一步研究的内容。同时,对于无人机影像拼接来说,由于三维建筑因拍摄角度不同存在投影差,因此将位于三维建筑上的特征点作为同名像点进行拼接容易造成“错位”,如何剔除三维建筑物上的特征点也是需要进一步研究的内容。
| [1] | Zitova B, Flusser J. Image Registration Methods: A Survey [J]. Image and Vision Computing, 2003, 21:977-1 000 |
| [2] | Zhang Yongjun. Geometric Processing of Low Altitude Remote Sensing Images Captured by Unmanned Airship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 284-288(张永军. 无人驾驶飞艇低空遥感影像的几何处理[J]. 武汉大学学报·5信息科学版, 2009, 34(3): 284-288) |
| [3] | Yang Heng, Wang Qing. A Novel Local Invariant Feature Detection and Description Algorithm[J]. Chinese Journal of Computers, 2010,33(5):935-943(杨恒,王庆. 一种新的局部不变特征检测和描述算法[J]. 计算机学报,2010,33(5):935-943) |
| [4] | Lowe D G. Object Recognition from Local Scale-invariant Feature[C]. International Conference on Computer Vision, Corfu, Greece, 1999 |
| [5] | Lowe D G. Distinctive Image Features from Scale-invariant Keypoints [J]. International Journal of Computer Vision, 2004, 60(2):91-110 |
| [6] | Mikolajczyk K, Schmid C. A Performance Evaluation of Local Descriptors [J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2005, 27(10):1 615-1 630 |
| [7] | Azad P, Asfour T, Dillmann R. Combining Harris Interest Points and the SIFT Descriptor for Fast Scale-invariant Object Recognition[C]. Intelligent Robots and Systems 2009, IEEE/RSJ International Conference on IEEE, St Louis, Missouri, USA,2009 |
| [8] | Chen Mengting, Yan Dongmei, Wang Gang. Algorithm of High-resolution Remote Sensing Image Matching Based on Harris Corner and SIFT Descriptor[J]. Journal of Image and Graphics, 2012, 17(011): 1 453-1 459(陈梦婷, 闫冬梅, 王刚. 基于 Harris 角点和SIFT描述符的高分辨率遥感影像匹配算法[J]. 中国图象图形学报, 2012, 17(011): 1 453-1 459) |
| [9] | Harris C, Stephens M. A Combined Corner and Edge Detector[C].Alvey Vision Conference, Manchester,UK, 1988 |
| [10] | Beis J, Lowe D G. Shape Indexing Using Approximate Nearest-neighbour Search in High-dimensional Spaces [C]. Conference on Computer Vision and Pattern Recognition, Puerto Rico, 1997 |
| [11] | Matas J, Chum O. Randomized RANSAC with Td,d Test [J]. Image and Vision Computing, 2004, 22:837-842 |
| [12] | Noble J A. Finding Corners [J]. Image and Vision Computing, 1988, 6(2): 121-128 |
| [13] | Smith S M, Brady J M. SUSAN—A New Approach to Low Level Image Processing [J]. International Journal of Computer Vision, 1997, 23(1):45-78 |
| [14] | Lan J, Zhang M. Fast and Robust Corner Detector Based on Double-circle Mask [J]. Optical Engineering, 2010, 49(12): 1 127-1 134 |
| [15] | Trajkovic M, Hedley M. Fast Corner Detection [J]. Image and Vision Computing, 1998, 16:75-87 |
 2015, Vol. 40
2015, Vol. 40



