文章信息
- 刘利敏, 宫辉力, 余洁, 陈蓓蓓
- LIU limin, GONG Huili, YU Jie, CHEN Beibei
- 一种PSInSAR干涉测量公共主影像选择新方法
- A New Optimization Selection Method of Common Master Image for PSInSAR Interferometry
- 武汉大学学报·信息科学版, 2015, 40(12): 1594-1599,1612
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1594-1599,1612
- http://dx.doi.org/10.13203/j.whugis20140049
-
文章历史
- 收稿日期: 2014-03-10

2. 首都师范大学资源环境与旅游学院, 北京, 100048;
3. 首都师范大学资源环境与地理信息系统北京市重点实验室, 北京, 100048
2. College of Resources Environment and Tourism, Capital Normal University, Beijing 100048, China;
3. Beijing Key Laboratory of Resource Environment and Geographic Information System, Capital Normal University, Beijing 100048, China
PSInSAR技术[1]由于能逐步分离时序影像大气延迟、轨道误差及DEM误差,在区域地表形变探测上具有巨大的技术优势。为提高形变监测精度,PSInSAR技术通常使用二十几景甚至更多影像,选择其中一幅为主影像,将其他影像与主影像进行干涉计算。因此,主影像的选择优劣,直接影响干涉图质量和后续的形变信息提取。
对于主影像的优化选取,目前主要围绕去相干因素选择及模型组织形式两个方面进行。Zeber等[2]指出引起时序SAR影像失相干的因素主要为时间基线、空间有效基线、多普勒(Doppler)中心频率及系统热噪声;Ferretti等[1, 3]在PSInSAR提出之初主要基于时间基线进行公共主影像选取;Zhang[4]等利用时空基线距的相干性测度乘积进行主影像选择;Hooper[5]综合考虑时空基线及Doppler中心频率对SAR影像相干性的影响,利用三个因素相干测度乘积选取主影像。陶秋香[6]等利用时空基线及多普勒中心频率构建三基线矢量和最小模型进行主影像选择。潘斌等[7]利用空间聚类思想对时空基线和多普勒中心频率特征空间进行分析,选择主影像,但阈值设定较为主观,聚类方法也不够严密。龙四春[8]把GPS数据融合在综合最大相干系数主影像选取模型中以去除大气延迟影响。
在主影像选取时,去相干因素的模型组织方式对主影像选择结果也有较大影响。应用较多的综合相关系数模型及三矢量和模型等,分别以不同去相干因素相干性测度的乘积或加和形式构建主影像选取模型,以综合衡量时空间基线和Doppler中心频率差对影像间的相干性总体影响。但在表达多参数综合作用时,不论直接从参数和还是参数乘积的角度去衡量,以往研究均未给出完备的数学推理[2, 3, 4, 5, 6, 7, 8, 9]。为了构建更优的主影像选取模型,本文对去相干因素组织形式进行研究,根据质心思想,经过数学推导,提出一种去相干因素组织表达新方法,在采用相同去相干因素的前提下,通过与综合最大相干系数主影像选取方法的对比分析,验证本文方法的有效性。
1 SAR影像去相干因素分析在PSInSAR干涉测量中,主辅影像相干性越好,干涉测量结果越可靠;反之,去相干越严重,形变监测能力越差。除因重复轨道干涉测量引起的时间去相干外,电磁波穿过路径的大气特征和几何成像位置等均会导致影像去相干。时间基线越长,两次成像地表形变及气候条件差异越大,去相干越严重;空间基线越大,雷达对地面入射角差异越大,几何去相关越严重;Doppler中心频率差异越大,去相干也越严重。干涉对相干性主要受雷达系统热噪声、时空基线距、Doppler中心频率的影响。因此,从时序SAR影像中选取主影像,需综合考虑各去相干因素的影响,选择一幅与其他影像总体相干性最大的影像。
时空基线、Doppler频率差对影像间相干性的数值测度,用分段函数表达:

式中,x为去相干因素;a为去相干因素对应临界值;f(x,a)为该去相干因素对影像间的相干性测度。
当基线距及Doppler频率差小于对应临界值时,取值越大,影像间相干性越小;当超过临界值时,相干性测度为0,完全失相干。临界值与SAR影像类型相关,空间垂直基线计算公式为BC=λρ/2Rcos2θ,ASAR影像空间垂直基线为935 m,时间基线多为6~9 a,ASAR影像Doppler中心频率差临界值为1 652 Hz。
f(T,Tc)、f(B,Bc)、f(D,Dc)分别表示两幅影像间的时间基线、空间有效基线以及Doppler频率差的相干性测度。
系统热噪声主要由雷达系统增益、天线特性等固有特性决定,对固定雷达系统而言,系统热噪声对所有SAR影像去相干程度一致,因此在主影像选择时,可不加以考虑,也可设为常值。
2 改进的最优主影像选取模型 2.1 综合最大相关系数模型选定参与主影像选择的去相干因素之后,将去相干因素以一定的形式进行组织,通过计算,选择一幅与其他影像总体相干程度最高的主影像,以达到最优总体干涉效果。由去相干因素相干性测度表达式(1)可知,在临界基线取值范围内,三种去相干因素与相干性测度呈单调递减关系。应用广泛的综合最大相干系数方法正是据此利用所有辅影像与待选主影像的去相干因素相干性测度乘积和的形式构建模型,进行主影像优化选取,如式(2):
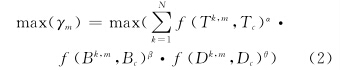
式中,N为影像数;m为待选主影像;Tk,m、Bk,m、Dk,m为第k景与第m景影像的时、空基线距及Doppler中心频率差;而Tc、Bc、Dc表示两幅影像时空基线距及Doppler频率差临界值;α、β、θ 为各因素去相干指数因子,代表贡献权重,解决各因素对相干性贡献程度不一致的问题。
这种以相干性测度乘积的形式构建的主影像选取模型及后来提出的三基线加和求最小的主影像选择模型,均可获得相对不错的效果;但在综合衡量去相干多种因素总体影响时,不论单纯从参数加和还是乘积的角度去衡量,相关研究并未给出完备的数学推理依据。
2.2 本文主影像选择模型本文在已有模型基础上,通过完整数学推导,构建一种去相干因素组织新方法,进行主影像优化选择。本文侧重于多种去相干因素相干性测度组织方法的研究。为便于对比本文方法和综合最大相关系数方法中去相干因素组织形式对选取结果的影响,在两种方法中分别采用相同的去相干因素,即均设定系统热噪声为常数,选择传统时间基线、空间垂直基线和多普勒中心频率进行主影像选取试验。
物理学中,常利用物体质心来代替物体所有点进行研究,以忽略物体复杂形状给研究带来的不便。由于时空基线距及Doppler频率差中单个因素与影像间的总体相干测度均呈单调关系,且一定程度上相互独立,因此可将三个去相干因素视为特征空间中的三个质点,借鉴质心思想,利用三个质点的质心代替三个独立质点,研究去相干因素对影像间的总体去相干影响,进而推导一种新的去相干因素组织模型,来衡量该景影像与待选主影像的综合相干性测度。
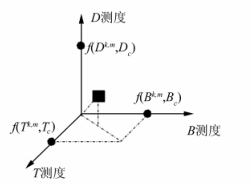
将时间基线、空间垂直基线及Doppler频率差的相干测度映射到三维立体空间。如图 1所示,坐标轴分别为 T测度、B测度及D测度。三坐标轴上的点(f(Tk,m,Tc),0,0)、(0,f(Bk,m,Bc),0)及(0,0,f(Dk,m,Dc))分别表示第k景与第m 景影像的时间基线相干性测度、空间基线相干性测度以及Doppler中心频率差相干性测度。
|
| 图 1 第k景与m景的相干性测度三维空间 Fig. 1 3D Space of the k and m Correlation Measure |
为了综合衡量三个相互独立的相干测度的总体影响,计算三个相干测度的质心,利用质心衡量总体相干测度。同时考虑到时空基线以及Doppler中心频率差对影像去相干贡献的差异, 引入不同去相干因素的贡献权重,在立体空间中,权重视为三个质点对应的质量,而三个相干性测度为对应矢径。
设时空基线距、Doppler频率差的权重分别为 δ、ε、φ,根据质心计算公式,第k景与第m影像的相干性测度的质心Zk,m位置如式(3)。由于质心Zk,m的三个坐标轴的值均为对应的相干性测度,因此质心到原点的距离,即为第k景与第m景影像的综合相干测度如式(4)。
本文根据质心思想构建主影像选取模型,以与其他影像综合相干测度最大为原则进行主影像选择,模型表达如式(5)。PSInSAR干涉测量一般要求不低于25景影像。衡量影像是否为最佳主影像时,在满足SAR影像完全不相干数量最少的前提下,要求根据本文模型计算得到主影像与其他辅影像总体相干性测度最大。
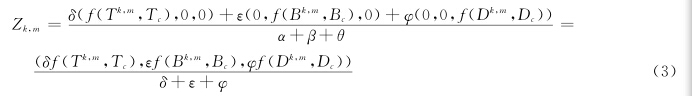

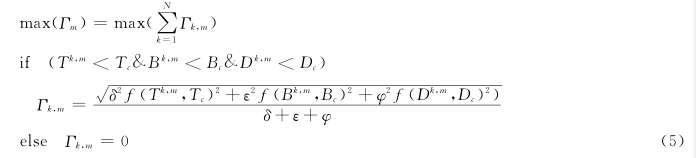
为了验证本文方法的有效性,选取2003~2009年北京地区28景ENVISAT ASAR降轨影像进行主影像选择试验,影像覆盖北京平原区,研究区范围为80 km×100 km,并以综合最大相关系数模型为对比试验。
3.1 本文模型及综合相关系数模型结果以处于时间中间的第15景(2007年9月5日获取)影像为参考基准,计算其他27景影像与参考基准的时空基线距以及Doppler频率差,如图 2所示。

|
| 图 2 影像集时空基线距及Doppler中心频率差 Fig. 2 Temporal-space Baseline and Doppler Center Frequency Difference of Image Set |
图 2中,影像空间基线距最大为1 627.3 m;时间基线最大达1 925 d;Doppler中心频率差最大为81.444 Hz。结合雷达系统参数,计算空间垂直基线及Doppler中心频率差临界值,分别为935.478 m及1 652.416 Hz。对于时间基线,认为6 a内影像间相干性可以接受,但在长时序地表形变监测中一般没有具体上限。试验数据最大 基线距及对应系统临界值见表 1。影像最大空间垂直基线超过临界值935.478 m,最大Doppler频率差81.444 Hz,远小于临界值1 652.416 Hz。为提高相干性测度数值表达的准确性,试验时,分别选择935.478 m、1 925 d及81.444 Hz作为模型中时空基线及Doppler频率差临界值Bc、Tc、Dc。
| 空间垂直基线/m | 时间基线/d | Doppler频率差/Hz | |
| 影像系统临界值 | 935.478 | 无 | 1 652.416 |
| 试验数据最大基线 | 1 627.3 | 1 925 | 81.444 |
根据式(2),利用综合最大相关系数模型选取 主影像。权重因子α、β、θ分别取(1,1,1)、(2,1,1)、(1,2,1)、(1,1,2)、(2,2,1)、(2,1,2)、(1,2,2)、(2,2,2)8种组合,分别以1~28景影像为待选主影像,计算8组权重组合下的综合相关系数γm,以及8组权重组合下的综合相关系数均值,并对28景影像的综合相关系数均值进行大小排序。图 3(a)为8组权重组合下,各影像为待选主影像时的综合相关系数γm以及8组综合相关系数均值曲线图;图 3(b)为各影像综合相关系数均值由大到小排序曲线。从图 3(a)可以发现,虽然不同权重组合下三种去相干因素的综合相关系数数值及变化曲线细节存在差异,但9条曲线总体变化趋势一致性较好,模型计算结果稳定;8组权重组合变化曲线及均值曲线均显示第22景影像的综合相关系数最大,排序为1,为该方法选取的最优主影像。

|
| 图 3 综合相关系数模型主影像选择选取结果 Fig. 3 Master Image Selection Result of the Correlation Coefficient Model |
根据式(5),δ、ε、φ按照前文中8组权重组合取值,利用本文方法分别计算各影像为待选主影像时8组权重下的综合相干性测度Γm,以及8组权重综合相干性测度均值,并对28景影像综合相干测度均值进行排序。同时根据ASAR雷达系统去相干临界值,计算各景影像为待选主影像时,与其他辅影像间的失相干个数。图 4(a)为8种权重组合下的综合相干测度以及8组综合相干测度均值的变化曲线,图 4(b)为对28景影像的综合相干测度均值由大到小的排序序号图。从图 4中可以看出,8组权重下,28景影像综合相干测度曲线虽在具体细节上存在差异,但是总体变化趋势非常一致,均在第20景影像处获得最大值,表明本文模型较为稳定,权重取值差异不会导致主影像选择结果的显著不同。

|
| 图 4 本文模型主影像计算结果 Fig. 4 Selection Result of Master Image of the Method Proposed |
根据本文方法计算得到的综合相干测度均值及与其他影像的不相干个数,进行主影像选取。如图 5所示,第20景影像与其他影像不相干个数为0,且综合相干测度均值最大,排序为第1,表明该影像与其他影像总体相干度最好,该景影像即为本文模型计算得到的最优主影像。对于综合相关系数模型选取的第22景影像,根据本文方法计算结果,总体相干测度排序仅为第4,且与第4景影像空间基线距超过临界值,完全失相关,因而第20景影像与其他影像的总体干涉效果优于第22景。

|
| 图 5 各影像综合相干测度均值排序 序号及不相干个数 Fig. 5 Average Coherence Sort Sequence Number and the Number of Decoherent Images for Each Image by the Model Proposed |
为定量评价第22及第20景影像与其他影像的总体干涉效果,分别以这两景影像为主影像做干涉计算,干涉图如图 6所示。分别对以第22及第20景影像为主影像时,与其他辅影像的时空基线距及Doppler中心频率差最大值、最小值、均方差,以及所有干涉对相干系数均值进行统计,统计结果见表 2。图 6(b)中干涉条纹更加明显,总体干涉视觉效果优于图 6(a)。从表 2中的统计结果可以发现,第20景为主影像时,相干系数均值也大于第22景影像,时空基线距及Doppler中心频率差的最大值均小于第22景影像为主影像时的对应值,进一步表明第20景影像与辅影像间的总体干涉效果优于第22景影像。试验结果表明,本文利用质心思想,将三去相干因素投影到三维空间,以三个质子的质心代替三去相干因素进行完备的数学推导和模型组织,构建去相干因素组织模型,在衡量三去相干因素对影像去相干的总体影响时,与传统直接以去相干因素乘积进行描述的方法相比更为合理。

|
| 图 6 第22景及20景影像为主影像的干涉图 Fig. 6 Interferograms with Respect to the Master Images of No. 20 and No.22 |
| 影像编号 | 基线 | 最大值 | 平均值 | 标准差 | 相干系数均值 |
| 综合相关系数 模型结果编号22 |
T | 1 645 | 681.25 | 621.99 | |
| B | 937.852 4 | 320.773 3 | 263.478 5 | 0.277 065 | |
| D | 61.179 2 | 10.393 2 | 11.095 2 | ||
| 本文模型结果 编号20 |
T | 1 575 | 648.750 0 | 589.636 8 | |
| B | 861.337 9 | 356.931 2 | 242.382 9 | 0.394 043 | |
| D | 58.548 3 | 10.205 2 | 11.416 7 |
1) 在传统去相干因子的基础上,本文将每景影像与待选主影像的三个相干性测度映射到三维空间,将在立体空间的投影视为三个质点,利用质心代替三个质点来衡量三个相干性测度的综合作用,构建了一种新的去相干因素组织模型。与综合相关系数模型相比,本文模型选择得到的主影像与其他影像总体干涉效果更好。
2) 在相同去相干因子的基础上,本文以质心思想推导的去相干因子组织模型进行主影像优化选择,选取效果优于传统直接以去相干因子乘积进行主影像选择的效果,表明本文模型去相干因素组织方式较传统模型更为合理。
3) 在不同权重组合下,本文模型均可获得一致的主影像选取结果,表明本文模型是稳定和可靠的。
| [1] | Ferretti A, Prati C, Rocca F. Permanent Scatterers in SAR Interferometry [J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1):8-20 |
| [2] | Zeber H A, Villasenor J. Decorrelation in Interferometric Radar Echoes [J]. IEEE Transactions on Geosciences and Remote Sensing, 1992, 30(5):950-955 |
| [3] | Ferrettia P C, Rocca F. Non2linear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 38(5): 2 202-2 212 |
| [4] | Zhang Hua, Zeng Qiming, Liu Yihua. The Optimum Selection of Common Master Image for Series of Differential SAR Processing to Estimate Long and Slow Ground Deformation[C]. IGARSS 2005,Seoul, Korea,2005 |
| [5] | Hooper A, Segall P, Zebker H. Persistent Scatterer Interferometric Synthetic Aperture Radar for Crustal Deformation Analysis with Application to Volcan Alcedo Gala'Pagos[J]. Journal of Geophysical, 2007, 112(7):1-21 |
| [6] | Tao Qiuxiang, Liu Guolin. A New Method to Optimize and Select Common Master Images in PSInSAR [J]. Geomatics and Information Science of Wuhan University, 2011, 36(12):1 456-1 460 (陶秋香, 刘国林. PSInSAR公共主影像优化选取的一种新方法[J].武汉大学学报·信息科学版, 2011, 36(12):1 456-1 460) |
| [7] | Pan Bin, Shu Ning. Cluster Analysis for Selection of Time Series Interferometric SAR Imagery[J]. Jounal of Applied Sciences-electronics and Information Engineering, 2010, 28(5):501-506 (潘斌, 舒宁.聚类分析用于序列SAR干涉相对选取[J].应用科学学报, 2010, 28(5):501-506) |
| [8] | Long Sichun, Liu Jingnan, Li Tao. Method for Optimum Selection of Common Master Acquisition for PSDlnSAR Fusing GPS Data [J]. Journal of Tongji University (Natural Science), 2010, 83(3):453-458 (龙四春, 刘经南, 李陶.融合GPS数据的PS-DInSAR公用主影像的优化选取 [J].同济大学学报·自然科学版, 2010, 83(3):453-458) |
 2015, Vol. 40
2015, Vol. 40



