文章信息
- 吴文豪, 王明洲, 李沙, 侯爱羚
- WU Wenhao, WANG Mingzhou, LI Sha, Hou Ailing
- 滑动聚束模式SAR影像干涉处理方法
- Analysis of Sliding Spotlight SAR Interferometry
- 武汉大学学报·信息科学版, 2015, 40(12): 1588-1593
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1588-1593
- http://dx.doi.org/10.13203/j.whugis20140012
-
文章历史
- 收稿日期: 2014-01-03

星载合成孔径雷达(SAR)系统在过去的几年里得到迅速发展,获取的海量数据可为光学遥感提供重要的数据补充。与光学遥感不同,SAR系统是根据多普勒频移原理,利用接收到的相干回波数据合成一个更大孔径的天线,从而实现了方位向分辨率的提高。2006年以来,陆续发射的COSMO-Skymed卫星、TerraSAR-X卫星、Radarsat-2等卫星具备了聚束模式成像能力,影像分辨率可达1 m[1]。卫星成像模式的多元化也进一步刺激了干涉技术的发展,干涉对象不再是单一的条带模式数据,而是朝着多传感器多种成像模式干涉的方向发展[2, 3, 4, 5]。Gatelli首先在波数域空间讨论了雷达影像干涉的必要条件;在此理论基础上,Arnaud实现了ERS-ASAR的干涉处理,Bamler针对Radasat卫星ScanSAR成像模式,提出ScanSAR成像模式的多普勒中心频率估计方法和干涉处理方法。Guccione分析了ScanSAR和IM数据的特性,并在此基础上研究了相应的配准方法,最后得到了WSM/IM 干涉图。随着星载滑动聚束模式成像的实现,该类数据的干涉与应用也成为研究的焦点。滑动聚束模式干涉和传统的条带模式的主要差别在于滑动聚束模式多普勒中心在方位向上是变化的[6, 7],进行重采样时需要根据滑动聚束模式数据多普勒中心变化规律对内插核进行调制,才能保证对影像插值的正确性。本文着重探讨滑动聚束模式影像点目标的多普勒历程,多普勒中心在方位线的变化规律,用一次多项式拟合多普勒中心分布,并通过模拟实验分析了非零多普勒中心对内插精度的影响。在开源软件DORIS基础上进行改进,完成TerraSAR-X卫星聚束模式影像干涉实验。
1 滑动聚束模式成像滑动聚束成像模式是指雷达波束在成像过程中始终照射成像区域的某个虚拟的焦点。在该模式下,天线辐射区在地面的移动速度既不像条带模式般与平台的速度相同,也不像聚束模式始终停留在一个目标点上,而是介于条带模式与聚束模式之间。该模式的优点就是通过对辐射区在地面速度的控制实现影像方位向分辨率和成像面积之间的平衡。
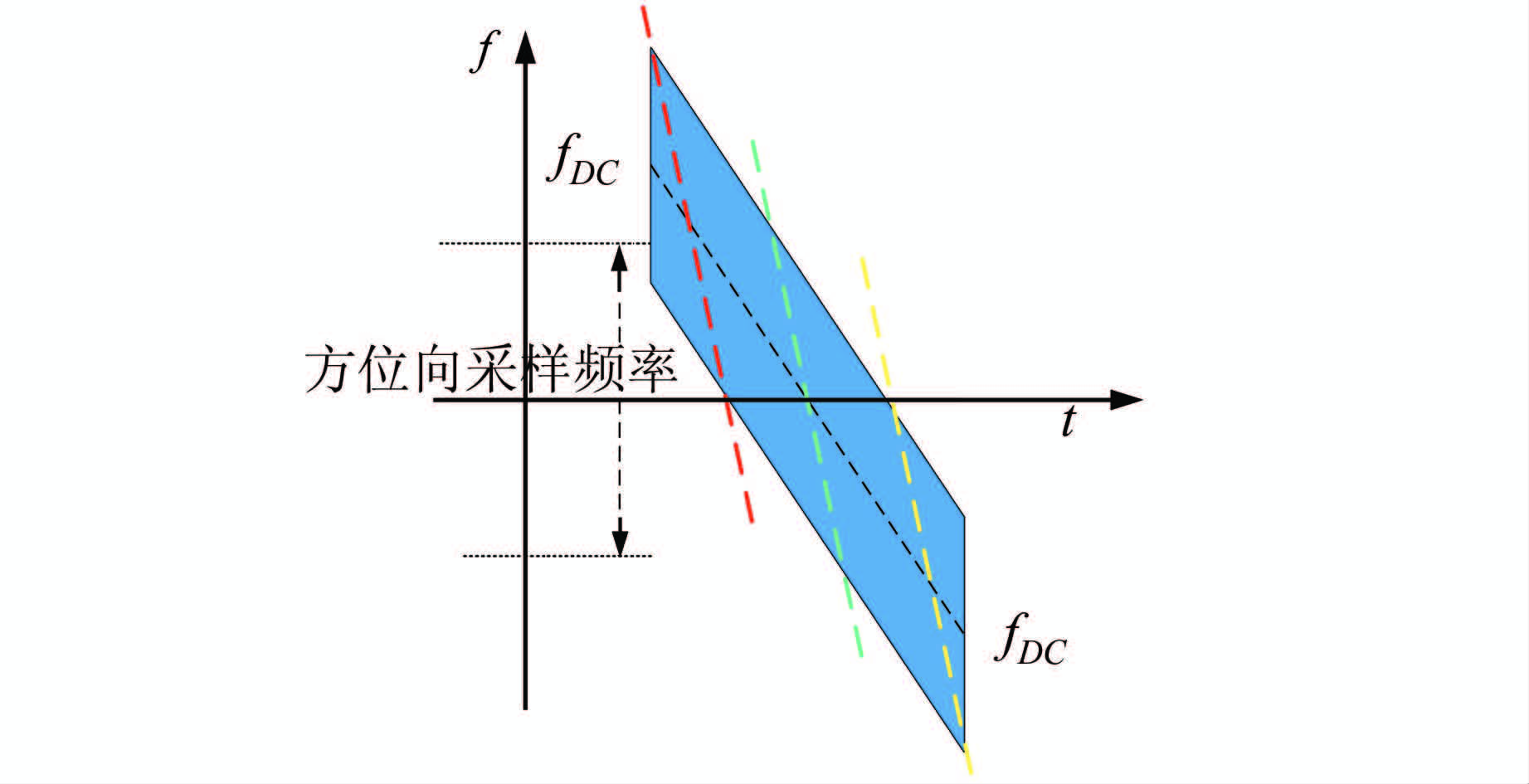
根据SAR成像原理,方位向多普勒历程与成像目标相对于卫星的径向速度有关。滑动聚束模式成像时方位向上的点目标多普勒历程均发生变化,如图 1所示。图 1中横轴为方位线时间t,纵轴为多普勒频率f。其中彩色虚线代表方位线上不同点目标的多普勒历程。黑色虚线表示方位向上的点目标回波多普勒中心。TerraSAR-X卫星参数文件所提供的雷达回波多普勒中心信息也证明了这一点[8],如图 2所示。图 2中多普勒中心在距离向基本上不变,而方位向呈线性递减趋势,变化范围为+6 000~-6 000 Hz。滑动聚束模式通过该方法延长了方位向成像时间,增加了多普勒带宽,进而提高了方位向分辨率。聚焦成像后,其影像频谱也与条带模式不同,特别是干涉处理时,需要考虑其频谱特性。
|
| 图 1 滑动聚束模式点目标多普勒历程 Fig. 1 Doppler History of Point Target of Sliding Spotlight Mode |

|
| 图 2 滑动聚束模式原始回波信号多普勒中心随时间变化示意图 Fig. 2 Doppler-centroid Variation with Time of Sliding Spotlight Mode Raw Data |
在聚焦成像过程中,滑动聚束成像模式利用方位参考函数点目标校正到零多普勒位置[9]。合成孔径雷达成像后点目标表达式一般为[10]:

式中,A0为常数;pr为距离向冲击响应的幅度;pa为方位向冲击响应的幅度,均为Sinc函数;τ、η分别为方位向、距离向参考时间;λ为雷达波长;fDC为多普勒中心;R0为传感器到点目标的零多普勒距离。
式(1)中的包络表明,目标位于τ=2R0/c,η=0处时,可见目标被校正至零多普勒位置;其指数项表明SAR距离线为基带信号,而方位线受到fDC的影响,若fDC不为零,则导致聚焦复影像中引入线性相位,其方位线不再是基带信号。然而,滑动聚束成像模式与条带模式不同,其回波多普勒中心fDC在方位向并不是固定值,致使聚焦影像方位线成为时变信号。值得注意的是,由于方位向采样频率不足,多普勒中心变化导致了影像方位线频谱出现混叠效应,混叠区域中的每一信号分量移至基本频率区域,如图 3所示。但这并不影响信号的正确重建。

|
| 图 3 聚焦影像方位线频谱 Fig. 3 Spectra Property of Focused Azimuth Signal |
滑动聚束模式影像的时频特性也可以通过方位线的短时功率谱体现[11]。图 4为TerraSAR-X影像的128条方位线短时功率谱平均处理后的结果。从图 4中可以看出,功率谱峰值随方位向时间变化,方位线类似于调频信号,进一步说明了方位线为时变信号。尽管滑动聚束模式方位向采样频率(即脉冲重复频率)要高于点目标的回波多普勒带宽,但由于多普勒中心的变化,依然会出现图 4中方位线短时功率谱混叠的情况。所以针对方位线进行插值处理时,必须考虑其频谱的特殊性,选择正确的插值方法。

|
| 图 4 TerraSAR-X滑动聚束模式影像方位线短时功率谱 Fig. 4 Short Time Power Spectral Spectrum of Azimuth Lines in TerraSAR-X Sliding Spotlight Mode Image |
图像配准和重采样基于配准参数将一幅复影像经过重采样投影到另一幅复影像的图像空间,并且要求没有信息损失,是SAR干涉数据处理中的关键步骤。因雷达复信号数据具有有限带宽,复图像的实部和虚部均为高斯分布,为保存图像的统计特性和相位信息,对实部和虚部分别进行重采样[12]。但SAR影像重采样常用的插值函数具有低通滤波器的性质,只能进行基带信号插值(如SAR影像距离线)。根据奈奎斯特采样定理,认为采用Sinc函数形式的插值方式没有信息损失,但在数据处理时该函数产生截断,可能导致图像失真。为了解决插值函数截断产生的振铃效应,一般采用平滑窗对Sinc系数加权或者优化后的插值函数进行插值。如§1所述,非零多普勒中心引入了线性相位,方位线频谱发生偏移,非零多普勒中心为方位线频谱中心,进行重采样时仍然使用这些插值函数易导致相位信息发生泄露[13]。非零多普勒中心对方位线重采样精度的影响可以通过仿真实验来进行评估。本文参考TerraSAR-X卫星高分辨率模式(HS)成像参数(脉冲重复频率为8 200 Hz,多普勒带宽为7 323 Hz),根据影像幅度服从瑞利分布,相位服从均匀分布这一统计规律来模拟方位线信号,并通过低通滤波处理生成具有相关性的随机复信号[14]。因卫星数据方位线过采样系数(脉冲重复频率与多普勒带宽的比值)约为1.1,所以对模拟的信号进行11倍的过采样,得到参考信号μ,然后对参考信号进行10倍的降采样处理,再分别调制不同的载频,获取测试信号μs。最后对信号μs进行内插,得到估计信号μ。插值相位误差即为φ=arg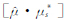 ,调制不同载频所产生的插值相位误差如图 5所示。当测试信号为基带信号时,理论上相位误差应该为零(如图 5红线所示);但事实上依然会存在一些因插值核所产生的信息泄露造成的相位误差(如图 5(a)蓝线所示),其值一般很小,可以忽略不计。而当测试信号调制为频带信号时,信号频谱被搬移至高频端,此时具有低通滤波性质的插值核频谱与测试信号频谱失配,插值时信息将大量泄露,导致相位误差增大。图 5(b)、5(c)、5(d)分别是调制了载频为800 Hz、1 600 Hz、2 400 Hz的插值相位误差示意图。可以看出,相位误差偏大;载波频率越高,相位误差越明显,即多普勒中心值越大,其内插相位误差越大。所以对非基带信号插值时,需要调制插值核以适应不同的信号频谱。对于时变信号,其局部信号频谱都是不同的。对此类信号内插时,插值核也要不断做出调整,适应信号的局部频谱。
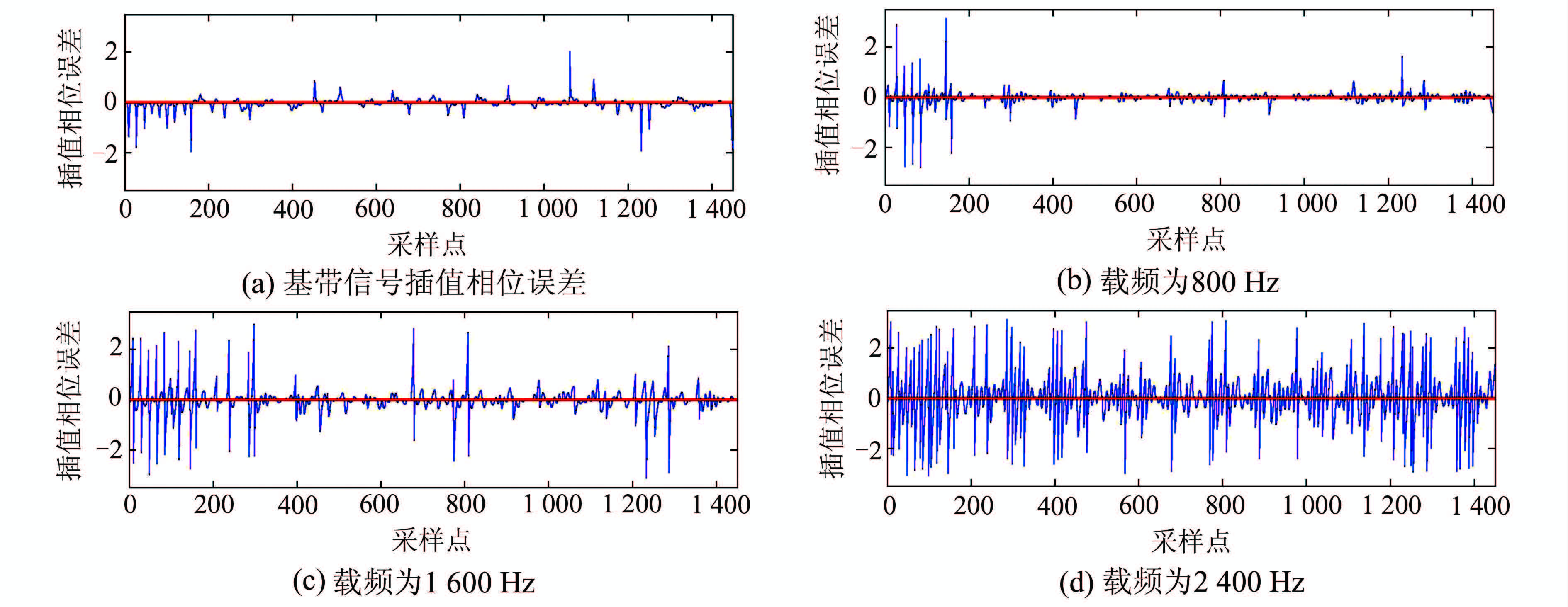
,调制不同载频所产生的插值相位误差如图 5所示。当测试信号为基带信号时,理论上相位误差应该为零(如图 5红线所示);但事实上依然会存在一些因插值核所产生的信息泄露造成的相位误差(如图 5(a)蓝线所示),其值一般很小,可以忽略不计。而当测试信号调制为频带信号时,信号频谱被搬移至高频端,此时具有低通滤波性质的插值核频谱与测试信号频谱失配,插值时信息将大量泄露,导致相位误差增大。图 5(b)、5(c)、5(d)分别是调制了载频为800 Hz、1 600 Hz、2 400 Hz的插值相位误差示意图。可以看出,相位误差偏大;载波频率越高,相位误差越明显,即多普勒中心值越大,其内插相位误差越大。所以对非基带信号插值时,需要调制插值核以适应不同的信号频谱。对于时变信号,其局部信号频谱都是不同的。对此类信号内插时,插值核也要不断做出调整,适应信号的局部频谱。
|
| 图 5 不同多普勒中心(载频)插值相位误差 Fig. 5 Interpolation Phase Errors Caused by Different Doppler-centroid (Carrier Frequency) |
模拟实验证明了多普勒中心是影像重采样正确与否的关键参数,正确获取多普勒中心表达式是重采样处理必不可少的一步。雷达回波多普勒中心变化是由卫星姿态角速率和角加速度决定的,由于卫星姿态的变化是缓慢且连续的,所以多普勒中心频率在整景影像内不会出现跳变,在实际的数据处理中,一般采用多项式进行拟合。考虑到SAR传感器性能的差异,多项式的阶数也可以适当做出取舍。对于星载条带成像模式数据(如ASAR,ERS卫星),一般认为卫星方位向波束姿态是不变的,多普勒中心仅在距离向发生变化,其多项式可以简化为:

式中,a0、a1、a2为多普勒中心相对于距离向时间的常数项,一次项系数和二次项系数;fDC为多普勒中心。
星载滑动聚束模式成像面积很小,如表 1中的数据只有10 km×5 km的覆盖范围,所以距离向多普勒中心变化可以忽略不计,多普勒中心表达式也可以简化处理。根据§1的分析可知,滑动聚束模式聚焦影像的方位线类似于载频随方位向时间变化的线性调频信号。所以滑动聚束数据多普勒中心多项式一般为:
| 拍摄时间 | 脉冲带宽 | 多普勒带宽 | 脉冲重复频率 | 首行多普勒中心值 | 末行多普勒中心值 | 方位向多普勒导数b0 | 影像中心多普勒中心a0 |
| 20090223 | 300 MHz | 7 358 | 8 300 | 3 220.8 | -3 213.3 | -8 605.2 | 3.798 08 |
| 20090212 | 300 MHz | 7 323 | 8 200 | 3 208.3 | -3 230 | -8 537.8 | -10.843 |

式中,b0为多普勒中心相对于方位向时间的一阶导数。
式(3)仅适用于TerraSAR-X卫星的滑动聚束模式数据。尽管可以从该卫星参数文件中提取出更高阶的多项式,但由于该卫星姿态控制较好,方位向多普勒中心近似于线性变化,使用一次多项式拟合多普勒中心分布已经可以满足干涉精度的需要[15]。对于其他可进行滑动聚束模式成像的卫星传感器,应根据多普勒中心变化情况来选取合适的多项式阶数。对SAR复影像进行干涉重采样处理时,首先根据多普勒中心多项式计算对应的每个采样单元的多普勒中心值(多普勒中心即为方位向线频谱偏移量),再对方位线进行插值。常用的非基带信号内插方法一般有两种:(1)将信号先转到基带,插值后再将信号频谱搬移至初始中心频谱;(2)将基带滤波器直接移至信号中心频谱处。考虑到计算效率问题,工程应用中一般采用第二种方法对内插核进行调制,具体公式为:
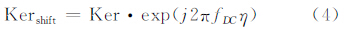
式中,Ker和Kershift分别为调制前和调制后的插值核。
采用插值核进行内插时,一般要在方位线上选取邻域内6~8个像素与内插核进行卷积运算。依据上述算法,完成影像重采样处理后,即可按照常规的干涉方法及流程进行去平地效应、干涉图滤波等处理。
3 实验分析本文采用的TerraSAR-X卫星滑动聚束模式影像拍摄地点为澳大利亚的艾尔斯巨石,周边为荒漠平原,相干性好。利用DORIS软件进行影像配准不存在问题。但是由于该软件的重采样模块只支持条带模式影像,其多普勒中心表达式如式(2),未考虑多普勒中心在方位向的变化。为实现滑动聚束模式影像的干涉,依据前述内插核调制理论实现滑动聚束模式重采样处理,即增加一个参数b0表示多普勒中心相对于方位向时间的导数,见表 1。重采样时根据多普勒中心表达式对方位线内插核进行调制,进而实现方位线的内插。影像干涉处理部分参数如表 1所示,其中干涉对的垂直基线为233.7 m,对应高程模糊度为34 m。
根据§2所述重采样插值理论和方法,对TerraSAR-X卫星数据进行干涉处理,其结果如图 6所示。在不考虑方位向多普勒中心变化的情况下,沿用条带模式处理方法对实验数据重采样后,再做干涉处理,结果如图 7所示。两幅干涉相位图均去除了平地效应。

|
| 图 6 内插核调制后生成的干涉相位图 Fig. 6 Interferometric Phase Image Produced After Modulating by Interpolation Kernel |

|
| 图 7 未进行内插核调制生成的干涉相位图 Fig. 7 Interferometric Phase Image Without Modulating by Interpolation Kernel |
因巨石周围为荒漠平原,且干涉影像对的高程模糊度为34 m,平原区的相位值应该基本上保持不变,如图 6所示。而图 7中出现了波状条纹,并且图像下部区域现象较为明显。这是因为图 7在处理过程中没有考虑多普勒中心在方位向的变化,影像下半部分的多普勒中心与重采样时默认的多普勒中心值相差较大,从而产生了插值相位误差。无论是模拟实验还是实际的数据处理,均证明了滑动聚束模式多普勒中心在方位向的变化是不可忽略的,否则会发生相位信息的混叠。
复相干系数也可作为衡量干涉图噪声的量化标准,相干系数的取值范围为[0,1]。若复相干系数趋近于0,表明失相干严重且相位噪声大;若相干系数趋近于1,表明相干性好且噪声小。理论上,如不考虑其他误差源,内插核与方位线频谱中心差异对干涉图复相干性的影响为:
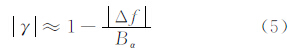
式中,Δf为插值核频谱中心与多普勒中心的差值;Bα为方位向多普勒带宽;γ为相干值。
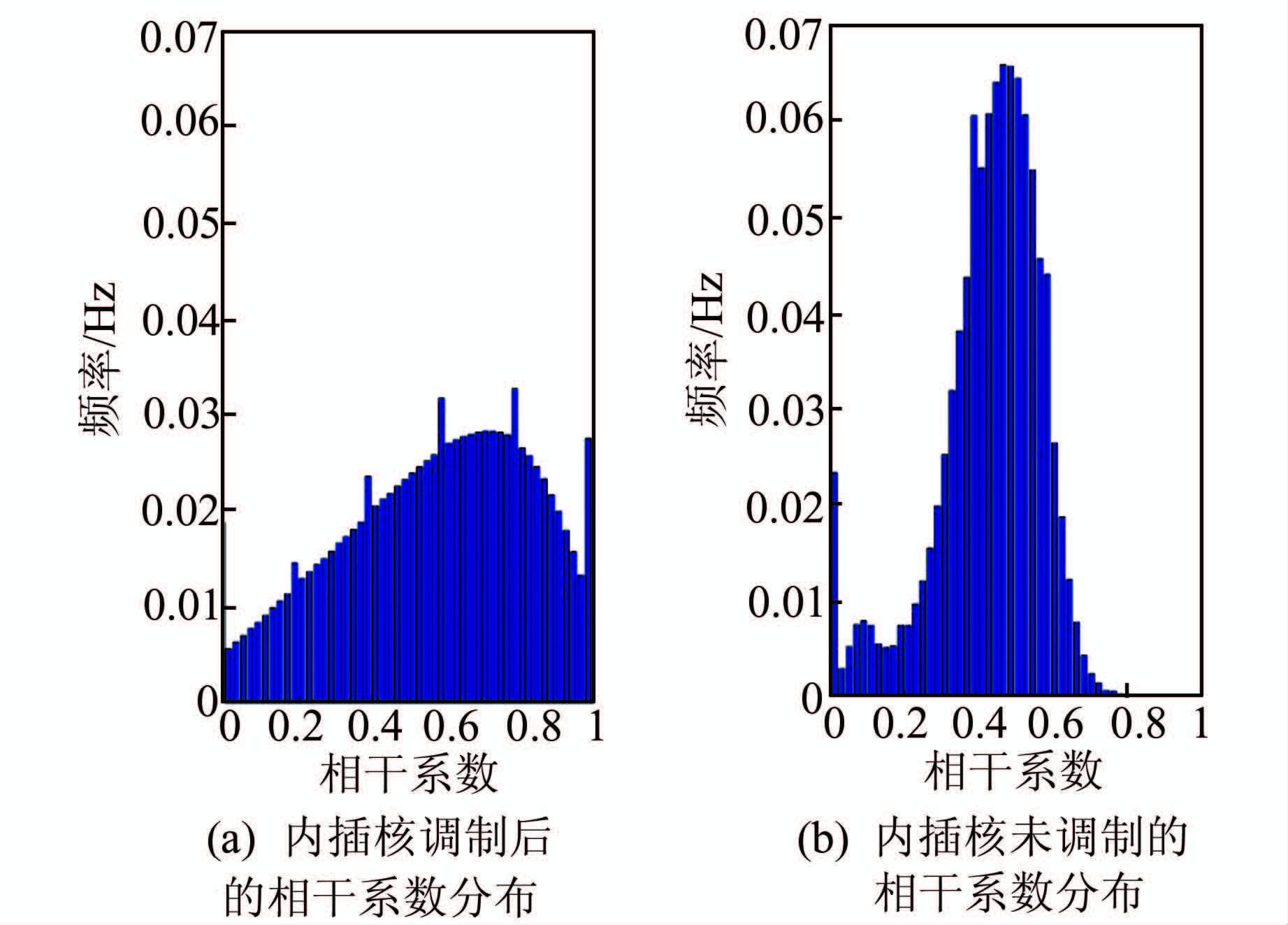
实际上,影像中每个像元所对应的多普勒中心都是不同的,对相干性的影响也不同,难以逐个统计。本文利用相干系数分布图来衡量干涉图噪声,如图 8所示。调制与未调制内插核干涉对的相干系数直方图相比较,可以看出内插核调制后的相干系数得到明显提高。
|
| 图 8 相干系数分布与内插核调制 Fig. 8 The Correlativity Between Coherence Histograms and Interpolation Kernel Modulation |
由于TerraSAR-X卫星空间基线一般在200 m以内,并且姿态控制水平较高,聚焦复影像中心的多普勒中心一般接近于零,因此对于该卫星的滑动聚束模式干涉处理,一般情况下无须考虑距离向、方位向滤波。然而对于其他具备聚束模式成像能力的SAR卫星,其干涉处理可能更复杂,则需要考虑采用距离向、方位向滤波以提高干涉图质量[16, 17]。
4 结 语作为零多普勒投影的滑动聚束模式影像,其干涉理论和处理流程与条带模式相同。但在影像重采样时需要考虑因方位向多普勒中心变化而导致的方位线局部频谱变化。本文在分析滑动聚束模式影像点目标多普勒历程的基础上,根据方位线信号频谱特性,基于DORIS软件实现了滑动聚束模式的聚焦复影像的重采样。本文分析了不进行内插核调制,不同多普勒中心所导致的相位插值误差,通过模拟数据的对比分析,证明多普勒中心在影像重采样时的重要性。实例干涉分析结果表明,采用一次多项式描述滑动聚束模式数据多普勒中心变化,可以确保辅影像在重采样过程中相位信息的完整性,从而实现滑动聚束模式影像的干涉。
欧空局哥白尼计划中的哨兵Sentinel-1A增加TOPSAR成像模式,其影像多普勒中心预计与滑动聚束模式一样,在方位向也会发生变化,其干涉处理方法也可以借鉴本文所述方法。
致谢:感谢Info Terra公司提供免费数据,感谢Delft大学提供免费的DORIS软件用于本文的实验分析。感谢夏耶博士,Ramon Hanssen教授对本研究提出的建议。
| [1] | Prats P, Scheiber R. High Precision SAR Focusing of TerraSAR-X Experimental Staring Spotlight Data[C]. IGARSS, Munich, German, 2012 |
| [2] | Gatelli F, Guarnieri M, Francesco F,et al. The Wavenumber Shift in SAR Interferometry[J]. IEEE Trans. Geosci. Remote Sens.1994, 32(4) : 855-865 |
| [3] | Arnaud A, Adam N, Hassen R, et al. ASAR ERS Interferometric Phase Continuity[C].IGARSS, Toulouse, France, 2003 |
| [4] | Holzener J, Bamler R. Burst-mode and Scan SAR Interferometry[J]. IEEE Trans. Geosci. Remote Sens. 2002, 40(9):1 917-1 934 |
| [5] | Rodriguez M, Prats P, Steinbrecher U, et al. Bistatic SAR Experiments with the TanDEM-X Constellation[C]. IGARSS, Munich, German, 2012 |
| [6] | Breit H, Fritz T, Balss U, et al. TerraSAR-X SAR Processing and Products[J].IEEE Trans. Geosci. Remote Sens.2010,48(2):727-740 |
| [7] | Wollsta S, Prats P, Bachmann M, et al. Scalloping Correction in TOPS Imaging Mode SAR Data[J]. IEEE Geosci. Remote Sens. Lett. 2012,9(4): 614-618 |
| [8] | Boerner E, Lord R, Mittermayer J, et al. Evaluation of TerraSAR-X Spotlight Processing Accuracy Based on a New Spotlight Raw Data Simulation[C]. IGARSS, Toulouse, France, 2003 |
| [9] | Eineder M, Adam N, Bamler R, et al.Spaceborne Spotlight SAR Interferometry with TerraSAR-X[J]. IEEE Trans.Geosci.Remote Sens. 2009, 47(5) :1 524-1 535 |
| [10] | Cumming I G, Wong F H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M].Boston:Artech House, 2005 |
| [11] | Wang Hongyu, Qiu Tianshuang, Chen Zhe. Nonstationary Random Signal Analysis and Processing[M]. Beijing: National Defence Industry Press, 2008:18-22 (王宏禹, 邱天爽, 陈喆. 非平稳随机信号分析与处理[M]. 北京:国防工业出版社, 2008:18-22) |
| [12] | Quegan S. Interpolation and Sampling in SAR Images [J]. IEEE Trans.Geosci.Remote Sens.1990, 28(4): 641-646 |
| [13] | Prats P, Scheiber R, Mittermayer J, et al. Processing of Sliding Spotlight and Tops SAR Data Using Baseband Azimuth Scaling[J]. IEEE Trans.Geosci. Remote Sens.2010,48(2):770-780 |
| [14] | Hassen R, Bamler R. Evalution of Interlation Kernel for SAR Interferometric Registration[J]. IEEE Trans. Geosci. Remote Sens.,1999,37(1): 318-321 |
| [15] | Werninghaus R. TS-X Project Manager. TerraSAR-X Basic Product Specification, TX-GX_DD_3302[OL].http://sss.terrasar-x.dlr.de/pdfs/TX-GS-DD-3302.pdf, 2010 |
| [16] | Jiang Houjun, Liao Mingsheng, Zhanglu, et al. High Resolution SAR Interferometric DEM Reconstruction with COSMO-SkyMed TanDEM Data[J]. Geomatics and Information Science of Wuhan University, 2011,6(9):1 055-1 058 (蒋厚军, 廖明生, 张路,等. 高分辨率雷达卫星COSMO-SkyMed干涉测量生成DEM的实验研究[J]. 武汉大学学报·5信息科学版,2011,6(9):1 055-1 058) |
| [17] | Qiu Zhiwei, Zhang Lu, Liao Mingsheng. An Algorithm for Spaceborne Interferometric SAR Signal Processing with Coherence Optimization [J]. Geomatics and Information Science of Wuhan University,2010,35(9):1 065-1 078 (邱志伟, 张路, 廖明生. 一种顾及相干性的星载干涉SAR 成像算法[J]. 武汉大学学报·5信息科学版, 2010,35(9):1 065-1 078) |
 2015, Vol. 40
2015, Vol. 40


