文章信息
- 巫兆聪, 杨帆, 巫远, 周小杰, 何晓宇
- WU Zhaocong, YANG Fan, WU Yuan, ZHOU Xiaojie, HE Xiaoyu
- 高程对TDICCD相机像移补偿影响分析
- The Influence of Elevation on the TDICCD Camera's Image Motion Compensation
- 武汉大学学报·信息科学版, 2015, 40(12): 1570-1574,1587
- Geomatics and Information Science of Wuhan University, 2015, 40(12): 1570-1574,1587
- http://dx.doi.org/10.13203/j.whugis20130667
-
文章历史
- 收稿日期: 2014-09-12

2. 青岛市勘察测绘研究院, 山东 青岛, 266033
2. Qingdao Geotechnical Investigation and Surveying Research Institute, Qingdao 266033, China
随着遥感技术的快速发展,各行业应用对遥感卫星光学成像质量的要求越来越高,传统CCD相机由于焦距长、像元尺寸小易造成积分时间短等问题;并且,采用相对小孔径容易带来光谱能量不足和信噪比低等问题。为此,高分辨率遥感卫星多采用TDICCD(时间延迟积分CCD)相机,并已展示出广阔的应用前景。
与普通CCD线阵不同,在高速动态成像时,TDICCD线阵的移动方向必须与目标像移方向一致,且移动速度大小也应匹配,任何误匹配都将导致图像模糊,影响图像质量。然而,地球自转运动、地面高程变化、轨道高度变化、卫星指向精度、姿态稳定度以及相机安装精度等因素,都将导致卫星对地成像时产生像移,影响光生电荷与像点的匹配,使图像质量下降甚至恶化[1, 2, 3]。
在空间分辨率和图像质量要求越来越高的情况下,高精度像移补偿技术已成为TDICCD相机获取高质量遥感影像的一个关键技术。国内外研究中关于像移补偿的计算方法主要包括:(1)坐标转换方法,主要通过坐标系之间的过渡矩阵建立物像之间的几何模型;(2)光线追迹法,采用数学方法描述像移过程中光线的传播过程[4];(3)基于联合变换相关器的测量方法,由Janschek等人提出,通过实时记录焦平面上的像移信息对图像进行相关运算得到像移[5]。我国研究人员计算像移补偿参数主要采用空间坐标转换方法,并做了大量的研究工作。王家骐等通过坐标变化的方法,建立从地面景物到像面的7个坐标系的线性变换,推导出一种高精度像移速度计算方法[6, 7];袁孝康基于地球圆球模型的假设推导了星下点、方位偏移和俯仰偏移成像下偏流角和像移速度的计算模型[8];王志刚等根据轨道方程推导了卫星偏流角的计算模型,研究了偏流角随纬度变化的规律及补偿方法[9];龙夫年、仲惟超等提出了结合飞行器姿态的高精度像移补偿参数计算模型[10, 11, 12]。
综合国内外研究现状,像移补偿的关键在于实时对TDICCD相机在轨成像时像移速度、偏流角和积分时间等参数的计算,其计算精度决定像移补偿的精度,影响遥感影像的质量。而目前大多数像移补偿计算模型是在将地球理想化为参考椭球模型,将卫星星下点作为像点对应的地面成像点的情况下,采用球面几何的方式进行推导计算。事实上,由于地面高程的影响,像点对应的地面成像点会与卫星星下点发生偏移,成像时刻的像移补偿参数会产生误差,影响相机的像移补偿和光学成像质量。
基于上述分析,本文在参考椭球面下的成像矢量模型基础上,建立考虑地面高程影响下的成像矢量模型,计算像点对应地面成像点的坐标及像移补偿参数,分析高程对偏流角、积分时间和像移速度等像移补偿参数的影响。在上述计算分析流程和全球高程模型数据的基础上,综合考虑像移补偿参数精度对高程误差的要求,星上存储空间及高程查询速度等因素,讨论星载DEM的生成。
1 顾及高程的像移补偿模型建立在考虑地面高程的情况下,TDICCD相机像点对应地面成像点的位置会发生偏移,如图 1所示。在将地球理想化为参考椭球模型的情况下,像点P对应的地面成像点为T',而考虑地面高程时地面成像点为T,两种情况下像点P对应的地面成像点经纬度坐标和高程值存在差异,且不同于卫星星下点。

|
| 图 1 TDICCD相机成像矢量示意图 Fig. 1 Schematic of TDICCD Camera’s Imaging Vectors |
本文利用TDICCD相机成像矢量关系,首先建立参考椭球下的成像矢量模型,其次计算在考虑地面高程情况下像点对应地面成像点的经纬度和高程值,在此基础上,计算此像点的像移速度、偏流角、积分时间等像移补偿参数。
1.1 参考椭球面下成像矢量模型在地球参考椭球面模型下,本文建立像点i、相机Oc、卫星Os和地面点T的矢量模型。图 1为相机成像时的矢量示意图。图 1中,Rpi为像面中心Op指向像点i的矢量,Rci为相机中心Oc指向像点i的矢量,Rcp为相机中心Oc指向像面中心Op的矢量,Rct为相机中心Oc指向目标T的矢量,Rst为卫星质心Os指向目标T的矢量,Rsc为卫星质心Os指向相机中心Oc的矢量,Ret为地球质心Oe指向目标T的矢量,Res为地球质心Oe指向卫星质心Os的矢量。建立它们之间的矢量关系式:
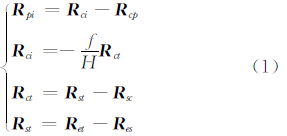
式中,f为TDICCD相机焦距;H为相机中心到地面成像点的距离。
将矢量Rst在轨道坐标系下表示为:

式中,RIet为矢量Ret在地心赤道坐标系下的表示;AOI为地心赤道坐标系到卫星轨道坐标系的变换矩阵,AOI=Cy(-uo-π/2)Cx(io-π/2)Cz(Ωo)。其中,io为卫星轨道倾角,Ωo为升交点赤经,uo为纬度幅角,即近地点幅角ωo与真近点角fo的和;Cx、Cy、Cz分别表示绕x、y、z轴进行旋转变换的矩阵形式;ROes=[0,0,-r]T,为Res在卫星轨道坐标系中的表示;r=Ao(1-e2o)/(1+eocosfo),为卫星质心到地心的距离;Ao为轨道长半轴,eo为轨道偏心率。
将矢量Rst在卫星本体坐标系下表示为:

式中,AbO为卫星轨道坐标系到卫星本体坐标系的转换矩阵,AbO=Cz(ψ)Cy(θ)Cx(φ);ψ、θ和φ分别为卫星成像时的航偏、俯仰和翻滚三个姿态角。
在计算得到Rbst后,根据式(1)计算Rct,并将矢量Rct在相机坐标系下表示为:

式中,Rbsc为矢量Rsc在卫星本体坐标系下的表示;Mcb为相机安装矩阵。
根据式(1)可推导出Rci在相机坐标系下的表示为:

根据式(1)和式(5),有:

式中,Rccp为矢量Rcp在相机坐标系下的表示,Rcp=(0,0,-f);Rppi为矢量Rpi在像平面坐标系下的表示。
将式(3)~(6)代入式(2)中,有:
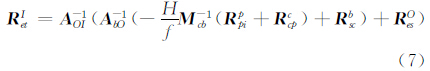
式中,A-1OI为AOI的逆矩阵,A-1bO为AbO的逆矩阵,M-1cb为Mcb的逆矩阵。
式(7)即为像点与对应地面成像点的矢量关系模型,卫星在确定时刻的轨道参数、在轨位置、姿态角、相机安装矩阵等参数已知,RIet由Rppi和H决定,即像点对应地面成像点坐标由像点坐标和轨道高度确定。
1.2 考虑高程的成像矢量模型及解算在参考椭球面成像矢量模型的基础上,本文建立考虑地面高程的成像矢量模型及解算流程,计算考虑高程时像点对应地面成像点的经纬度坐标和高程值。
通过RIet可获得像点对应地面成像点在地心赤道坐标系下的位置[X,Y,Z]T。将其转换为地心固连坐标系下的坐标值,表示为[x,y,z]T=A-1IeRIet,其中A-1Ie为AIe的逆矩阵,AIe=Cz(θt),θt为对应时刻点的格林尼治恒星时。地心固连坐标系与大地坐标系的变换关系为:

式中,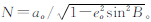 。将地面成像点的纬度B、经度L和高程h用像平面坐标xpi,ypi表示,并根据全球DEM数据,建立地面成像点经纬度坐标计算模型方程组:
。将地面成像点的纬度B、经度L和高程h用像平面坐标xpi,ypi表示,并根据全球DEM数据,建立地面成像点经纬度坐标计算模型方程组:
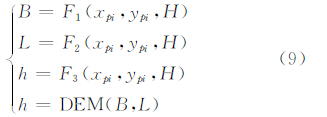
由于地面高程为离散模型,方程组须进行迭代运算,具体过程如下。
1) 令地面高程h=0,代入方程组计算初始经纬度值(B0,L0);
2) 根据(B0,L0)查询DEM中对应经纬度的高程h1;
3) 将h1代入方程组计算出另外一组经纬度值(B1,L1);
4) 比较步骤2)、3)中计算的两组经纬度值,若其经度差值或纬度差值小于限值,则计算结束;若大于限值,则将(B1,L1)作为初始经纬度值,重复进行2)、3)步骤,直至相邻两组B和L的差值小于限值。经过循环计算,得到像点对应地面成像点的经纬度值和高程值。
1.3 像移补偿参数计算基于像点坐标对应地面成像点的坐标计算后,建立像点在像平面坐标系中的矢量方程,计算像移速度矢量、偏流角、积分时间等像移补偿参数。
在相机对地成像过程中,地球自转运动使得像点在像面上的移动方向与卫星运动方向之间存在一定的夹角,即偏流角β,通常利用像移速度值Vp和偏流角β来描述像移速度矢量。
根据式(6)可推导Rpi在像平面坐标系下的表示为:

像移速度矢量通过矢量Rppi对时间求导,由于相机安装位置固定,相机安装矩阵的导数 =0,
=0,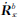 =0,相机中心到地面成像点距离的导数对像移速度产生的影响沿像平面法线方向,对像移速度计算没有影响,因此令
=0,相机中心到地面成像点距离的导数对像移速度产生的影响沿像平面法线方向,对像移速度计算没有影响,因此令 =0。像移速度矢量表示为:
=0。像移速度矢量表示为:
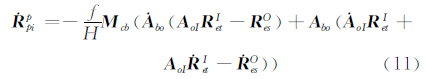
式中,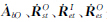 分别表示AbO、ROst、RIet、ROes对时间的导数。
分别表示AbO、ROst、RIet、ROes对时间的导数。
式(11)中,ppi包含3个方向的分量,可写作ppi=Vp1,Vp2,Vp3T。由于像点在像平面上,像移速度矢量可表示为Rp=Vp1,Vp2T。像移速度为:
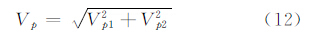
偏流角为:
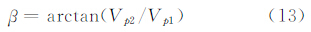
积分时间为:

式中,d为TDICCD相机像元尺寸。
通过上述成像模型的建立及像点对应地面成像点坐标的计算,提供在考虑高程情况下卫星在轨成像时实时计算像移补偿参数的方法与流程,为TDICCD相机高精度像移补偿提供基础。
2 高程对像移补偿参数影响分析在卫星轨道参数ao=6 879.106 km,Ωo=189.227°,io=97.395°,eo=0,ωo=0°以及卫星姿态角与姿态角变化率都为0的情况下,分别计算星载TDICCD相机在是否考虑高程情况下在重点地区的像移补偿参数,如北京石景山、河南嵩山、四川雅安和黄土高原等重点成像试验区域,计算结果见表 1。表 1说明了高程对成像积分时间会有一定的影响,而对偏流角影响很小。
| 成像区域 | 平均高程值/m | 不考虑地面高程 | 考虑地面高程 | 差值 | |||
| 偏流角 | 积分时间/ms | 偏流角 | 积分时间/ms | 偏流角 | 积分时间/ms | ||
| 北京石景山 | 73 | 2.828 728° | 1.014 187 | 2.828 728° | 1.014 032 | 0° | 0.000 155 |
| 河南嵩山 | 1 125 | 3.045 858° | 1.010 148 | 3.045 858° | 1.007 758 | 0° | 0.002 390 |
| 四川雅安 | 605 | 3.204 273° | 1.007 010 | 3.204 273° | 1.005 725 | 0° | 0.001 285 |
| 黄土高原 | 1 298 | 2.981 407° | 1.011 378 | 2.981 407° | 1.008 621 | 0° | 0.002 757 |
从像移补偿模型分析可知,像移补偿参数随着卫星的纬度幅角从0°~360°变化而周期性变化,分别计算相机的地面成像点在0°、30°和60°纬度圈上时不同高程值对应的像移速度、偏流角和积分时间,分析高程差值对像移补偿参数的影响规律。
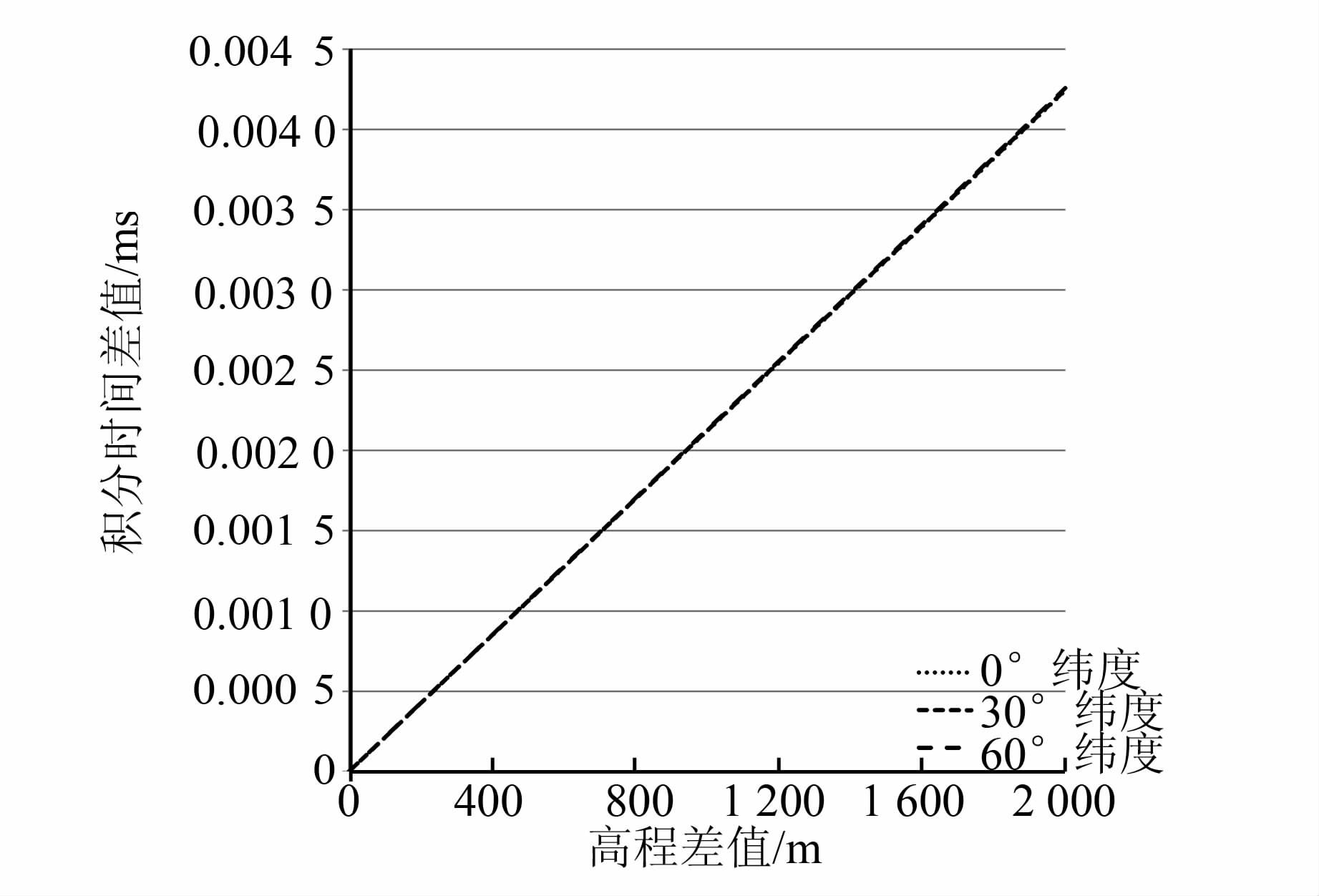
图 2和图 3分别表示地面成像点在0°、30°和60°纬度圈上不同高程值对应的像移速度和积分时间与高程为0情况下的差值,由于偏流角的差值约为0,在此不做具体分析。

|
| 图 2 不同高程值对应的像移速度差值 Fig. 2 D-value of Image Motion Velocity Corresponding to the Different Elevation Values |
|
| 图 3 不同高程值对应的积分时间差值 Fig. 3 D-value of Integration Time Corresponding to the Different Elevation Values |
像移速度和积分时间的差值变化趋势一致,随着高程差值增大而增加。针对不同成像情况下像移补偿参数的精度要求,从图 2、图 3中可分析得到地面高程值误差范围,以此作为依据判定像移补偿参数在不同精度要求下对地面高程精度的约束,在实际应用中可以在合理的误差范围内适当降低地面高程模型的精度,减小数字高程模型的数据量。
3 星载数字高程模型生成通过上述考虑高程的像移补偿计算模型及高程对像移补偿的影响分析,为使高程信息和高精度像移补偿计算模型应用于TDICCD相机在轨实时成像的像移补偿参数计算中,本文简单介绍星载DEM的生成。
由于全球数字高程模型数据量巨大,而航天器的存储空间有限,DEM内插查询须具有较高的时间效率,因此需在综合分析像移补偿参数对DEM的精度要求、航天器存储空间以及DEM查询速度的情况下,建立满足星载要求的数字高程模型。
本文使用的星载DEM数据源主要为SRTM3 V4.1,并配合使用ASTER GDEM和GTOPO30数据。为降低DEM的数据量,在数据源的基础上,增大高程采样间隔,建立较大格网间距的数字高程信息。本文分别建立了格网间距为1′、10′、15′、30′、1°、2°等多种星载DEM,以满足不同精度和不同存储空间要求的航天器。在实际应用中,可以将不同采样间隔的DEM配合使用,例如,根据成像任务将对地成像区域分为重点区域和普通区域,重点区域可采用小格网间隔的DEM,如1′、6′格网间隔的DEM,普通区域可采用相对较大格网间隔的DEM,如30′、1°格网间隔的DEM,这样既可以节约存储空间,又可以很好地满足像移补偿参数计算精度要求[13]。
4 结 语通过上述模型计算与分析地面高程影响像移速度和积分时间的计算结果,可以得出,如果不考虑地面高程信息将引起像移补偿参数失配,影响图像质量。因此,获取高质量和高分辨率的遥感影像,必须考虑高程对TDICCD相机成像质量的影响。本文建立的星载DEM可用于星载TDICCD相机精确在轨实时计算像移补偿参数,对高精度像移补偿和高质量遥感影像获取具有重要意义。
| [1] | Bao Haiming. The Way to Realize Time Delay and Integration Based on Area CCD[J].Optical Technique, 2006,32(8): 587-591(鲍海明. 基于面阵CCD积分延时(TDI)工作方式的实现方法[J]. 光学技术, 2006, 32(8): 587-591) |
| [2] | Wang Xinyi, Zhang Jianqing, Hu Yan, et al. Analysis of Geopositioning of Satellite Three-line Array CCD Caused by Drift Angle[J]. Geomatics and Information Science of Wuhan University, 2013,38(3):283-286 (王新义, 张剑清, 胡燕,等.偏流角对卫星三线阵 CCD 影像定位的影响分析[J]. 武汉大学学报·信息科学版, 2013, 38(3):283-286) |
| [3] | Yue Qingxing, Qiu Zhenge, Jia Yonghong,et al. In-orbit Imagery Simulation Method of Three-line-array TDICCD Carema[J].Geomatics and Information Science of Wuhan University,2010,35(12): 1 427-1 431 (岳庆兴, 邱振戈, 贾永红, 等. 三线阵 TDICCD 相机在轨成像数学仿真方法[J]. 武汉大学学报·信息科学版, 2010, 35(12): 1 427-1 431) |
| [4] | Toyoshima M, Jono T, Yamakawa S,et al.In-orbit Measurements of Spacecraft Microvibrations for Satellite Laser Communication Links [J]. Optical Engineering, 2010, 49(8):1-10 |
| [5] | Janschek K, Tchernykh V, Dybleenko S.Compensation of Focal Plane Image Motion Perturbations with Optical Correlatorin Feedback Loop[J]. Proceedings of SPIE, 2004, 5 570:280-288 |
| [6] | Yan Changxiang, Wang Jiaqi. Method of Coordinate Transformation for IM&IMC Calculation in Aerospace Camera System[J]. Optics and Precision Engineering, 2000,6(8):203-207 (颜昌翔,王家骐. 航相机像移补偿计算的坐标变换方法[J].光学精密工程, 2000,6(8):203-207) |
| [7] | Wang Jiaqi, Yu Ping, Yan Changxiang, et al. Space Optical Remote Sensing Image Motion Velocity Vector Computational Modeling [J]. Acta Optica Sinica, 2004, 24(12):1 585-1 589(王家骐,于平,颜昌翔,等.航天光学遥感器像移速度矢量计算数学模型[J].光学学报,2004,24(12):1 585-1 589) |
| [8] | Yuan Xiaokang. Calculation and Compensation for the Deviant Angle of Satellite Borne TDI-CCD Push Scan Camera[J]. Aerospace Shanghai, 2006,6:10-13 (袁孝康.星载TDI-CCD 推扫相机的偏流角计算与补偿[J].上海航天,2006,6:10-13) |
| [9] | Wang Zhigang, Yuan Jianping, Chen Shilu, et al. Study on Satellite Remote Sensing High Resolution Image Bias-angle and Its Compensation[J]. Journal of Astronautics, 2002,23(5):39-43(王志刚,袁建平,陈士橹,等.高分辨率卫星遥感图像的偏流角及其补偿研究[J].宇航学报,2002,23(5):39-43) |
| [10] | Long Funian, Zhang Wang, Liu Jianfeng. Effect of Satellite Control Accuracy on TDICCD Cameras [J]. Journal of Harbin Institute of Technology, 2002, 34(3): 382-384 (龙夫年, 张旺,刘剑峰. 卫星姿态精度对TDICCD相机的影响[J]. 哈尔滨工业大学学报,2002,34(3):382-384) |
| [11] | Zhong Weichao. The Effect Analysis of Spacecraft Orbit And Attitude Parameters on Optical Imaging[D]. Harbin:Harbin Institute of Technology, 2009(仲惟超.航天器轨道和姿态参数对光学成像的影响分析[D]. 哈尔滨:哈尔滨工业大学,2009) |
| [12] | Zhong W, Deng H, Sun Z, et al. Computation Model of Image Motion Velocity for Space Optical Remote Cameras[C]. ICMA,Changchun, China, 2009 |
| [13] | Hu Hai, Wu Yanlan, Hu Peng. Discussion of DEM Standards, Quality Theory and Conceptions[J]. Geomatics and Information Science of Wuhan University, 2011, 36(6):713-716(胡海, 吴艳兰, 胡鹏. 数字高程模型精度标准、质量理论和科学观念讨论[J]. 武汉大学学报·信息科学版,2011, 36(6):713-716) |
 2015, Vol. 40
2015, Vol. 40


