文章信息
- 翁寅侃, 李松, 杨晋陵, 易洪, 王虹, 马跃
- WENG Yinkan, LI Song, YANG Jinling, YI Hong, WANG Hong, MA Yue
- SAR辐射定标中角反射器RCS的快速求解
- Fast Solution to the RCS of Corner Reflector for the SAR Radiometric Calibration
- 武汉大学学报·信息科学版, 2015, 40(11): 1551-1556
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1551-1556
- http://dx.doi.org/10.13203/j.whugis20130613
-
文章历史
- 收稿日期: 2014-03-30

2. 昆明理工大学理学院, 云南 昆明, 650500;
3. 山东科技大学测绘科学与工程学院, 山东 青岛, 266590
2. School of Science, Kunming University of Science and Technology, Kunming 650500, China;
3. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
目前,合成孔径雷达(synthetic aperture radar,SAR)已经由定性遥感时代跨入了定量遥感时代[1, 2, 3],定标是实现SAR对地定量观测的不可缺少的技术[4],SAR辐射定标可以构建图像与地物后向散射系数的精确关系,是SAR定量化应用的前提[5]。通常,辐射定标场内布设一定数量的有源和无源设备来实现SAR辐射定标。角反射器具有相对稳定的、较大的雷达截面积(radar cross section,RCS),并且表现出与波长和尺寸无关的3dB波束宽度,因此,它成为SAR辐射定标中常用的无源定标设备[6- 8]。
由于作为SAR辐射定标的角反射器尺寸较大,一般为电大尺寸,因此,宜采用高频近似法。高频近似法如射线弹跳法(shooting and bounting ray,SBR)[9, 10]、高斯波束法(Gaussian beam,GB)[11, 12]和复射线法(complex ray,CR)[13, 14],分别要求的射线密度为350/λ2、25/λ2和4/λ2,其公式繁琐且计算效率低下。电磁仿真软件FEKO的做法也是对平板以λ/8大小的三角面元进行剖分后应用物理光学法(physical optics,PO)计算RCS,其效率也较低,同时消耗了大量的计算机内存。FEKO的多层快速多极子技术(multilevel fast multipole method,MLFMM)虽进一步提高了其效率,但在计算电大尺寸目标的RCS时其仍很耗费时间和内存。
针对平板结构的角反射器,本文通过结合几何光学(geometrical optics,GO)和Gordan面元积分法[15]提出了一种角反射器RCS的快速计算方法,可分为以下两步:(1) 利用GO对入射波和反射波进行射线追迹以确定每次入射场及其相对应的照明区域;(2) 利用Gordan面元积分法对每个照明区域求散射场并累加得到总RCS。该方法的主要优点:首先照明区域的确定简单快捷;其次无需对照明区域进行任何剖分,只需知道照明区域的轮廓就可以应用Gordan的围线积分进行该区域的RCS计算,然后对每个照明区域的RCS直接累加即可得到总的RCS。该方法容易实现且计算效率高,最终对比结果表明其准确有效。
1 理论方法RCS平方根的物理光学表达式为:
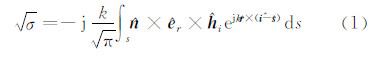
式中,σ表示RCS;k表示波数;S表示散射体的照明区;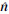 表示表面的外法向矢量;êr表示接收机的电极化方向单位矢量;ĥi表示入射波的磁场方向单位矢量;
表示表面的外法向矢量;êr表示接收机的电极化方向单位矢量;ĥi表示入射波的磁场方向单位矢量;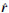 表示场点的位置矢量;î和ŝ分别表示入射方向和散射方向的单位矢量。
表示场点的位置矢量;î和ŝ分别表示入射方向和散射方向的单位矢量。
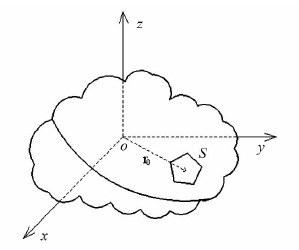
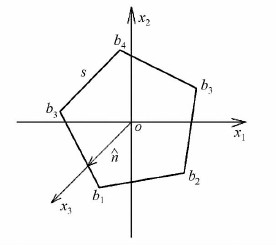
考虑目标照亮区内一小块平板面元的散射,如图 1所示。建立局部坐标系o-x1x2x3,如图 2所示,使坐标轴ox3沿面元的外法线方向 ,ox1x2位于面元内,不失一般性,原点o取在面元的中心处。
|
| 图 1 标照亮区的坐标系 Fig. 1 Coordinate System of the Illuminated Area |
|
| 图 2 平板面元的局部坐标系 Fig. 2 Local Coordinate System of the Surface Element |
设 r =r0+x,r0是局部坐标系原点的位置矢量,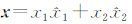 为源点在面元上的位置矢量,则式(1)变成:
为源点在面元上的位置矢量,则式(1)变成:
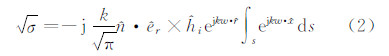
式中,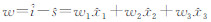 。
。
应用格林定理和欧拉公式可将式(2)中的面积分化成线积分。设面元为N边形,第n个顶点的位置矢量为 b n,并设bN+1=b1,Δbn=bn+1-bn,n=1,2,…,N。令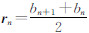 ,表示第n条边中点的位置矢量;an=Δbn,表示第n条边的长度和方向。可得平板面元的RCS平方根表达式:
,表示第n条边中点的位置矢量;an=Δbn,表示第n条边的长度和方向。可得平板面元的RCS平方根表达式:
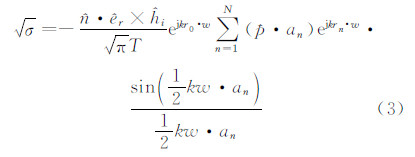
式中,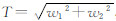 ,为w在平面上的投影长度;
,为w在平面上的投影长度;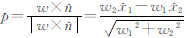 。
。
注意到,当因子T=0时,表达式(3)会出现奇异性。这就意味着在平板平面上没有 (î- ŝ )的分量,因此,这个表面与从源点到远场观察点逐渐延迟的等相位面相重合。换言之,表面上的相位并没有变化,因此,式(2)中的积分式就化为平板小面元的面积A。于是,在T=0的情况下,式(3)变为:
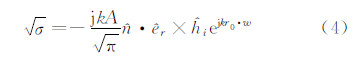
当入射方向、散射方向与面元外法向重合时,单站散射的表达式为:
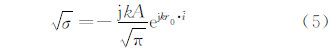
这样,只要求出每一块理想导体平板面元的含有相位信息的 RCS平方根,然后再直接相加,取模的平方,就可以得到散射体总的RCS,即
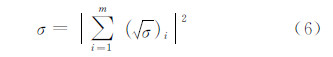
由上述推导分析可得:
1) 一般情况下,即T≠0时,采用式(3)计算RCS,此时,只需知道该多边形面元的所有顶点坐标及其外法向矢量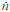 ,照亮该多边形面元的入射波方向和散射方向的单位矢量(î和ŝ ),还有入射波磁场方向和接收机电极化方向的单位矢量(ĥi和êr);
,照亮该多边形面元的入射波方向和散射方向的单位矢量(î和ŝ ),还有入射波磁场方向和接收机电极化方向的单位矢量(ĥi和êr);
2)当T=0时,意味着在平板平面上没有î - ŝ 的分量,即入射波方向与散射方向满足镜面反射,如垂直照射平板时可直接采用式(5)计算RCS;还有当照射一个直角型的二面角反射器时,第一个面的反射波入射到第二面也会导致T=0,此时须采用式(4)计算RCS,只需知道该多边形面元的面积A即可。
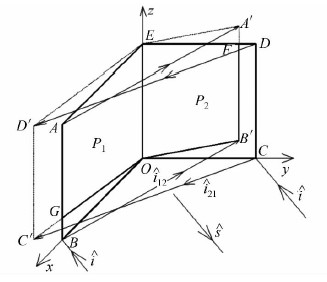
针对直角型二面角反射器,如图 3所示,已知P1(四边形ABOE)和P2(四边形OCDE)面的所有顶点坐标,利用GO确定照明区域。
|
| 图 3 利用GO确定照明区域 Fig. 3 Determination of Illuminated Area by the GO |
1) P1和P2面受直接来波î的一次照射。运用Gordan面元积分法分别对整块P1、P2平板(四边形ABOE和四边形OCDE)应用式(3)进行计算得到RCS的平方根 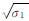 和
和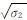 ;
;
2) P2面受到P1面反射波 12的二次照射。利用GO依次确定P1平板上各个顶点(O、B、A和E)在P2面上的投影点O、B′、A′和E,顺序连接这些点得到一个多边形OB′A′E′,然后求得多边形OB′A′E与P2面的交集(多边形OB′FE)。同理,P1面受到P2面反射波 21的二次照射时,多边形OEAG为最终照射区域。然后对这两个多边形(OB′FE和OEAG)应用式(4)进行RCS计算得到 σ12 和 σ21 ;
3) 利用GO可出现的最大反射次数小于或等于π/α (α为二面角)的最大整数[16]。因此,当二面角 在90°~180°时,至多发生二次反射,但当二面角在60°~90°时,会出现三次反射;
4) 最后应用式(6)把所有反射情况下的RCS平方根直接累加,取模的平方即可得到二面角反射器总的RCS。
上述步骤可类推至三面角反射器的RCS计算,只是三面角反射器存在着15种反射情况。
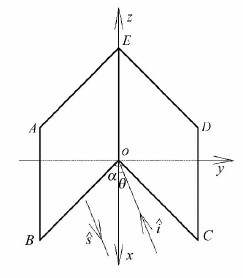
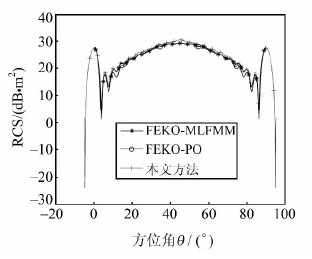
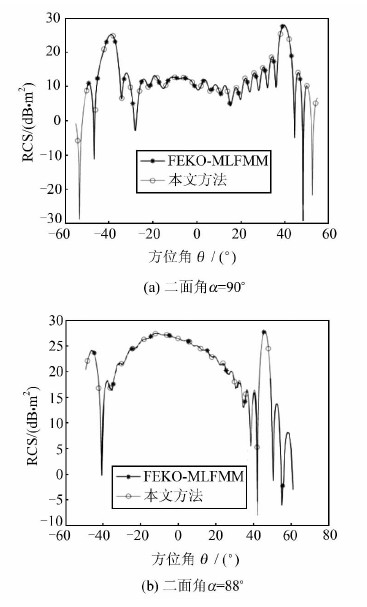
2 仿真结果验证本文采用上述方法对二面角反射器和三面角反射器分别进行了RCS计算。二面角反射器如图 4所示,x轴为二面角 α的角平分线,z轴与OE重合,ŝ为散射方向,入射波î垂直于z轴,与x轴夹角为θ。OB=OC=OE=1 m,二面角α=90°,频率为2 GHz,在VV极化下的仿真结果如图 5所示。将本文与FEKO仿真结果进行了比对,对应的偏差均值分别是-0.53 dB· 5m2和-0.94 dB· 5m2。若OB=45/k m,OC=30/k m,OE=0.5 m,k=2π/λ,二面角α=100°和α=88°,频率为9.4 GHz,在HH极化下的仿真结果如图 6所示,图 6(a)将Knott[17]方法与本文方法的结果进行了比对,两者的偏差均值几乎为0 dBsm;图 6(b)将FEKO与本文方法的结果进行比对,两者的偏差均值是-0.11 dBsm。从图 5~图 6中也可以看出,二面角无论是直角、钝角或锐角,本文方法与FEKO、文献[17]结果都基本吻合。
|
| 图 4 二面角反射器几何示意图 Fig. 4 Geometric Sketch of the Dihedral Reflector |
|
| 图 5 二面角α=90°时VV极化下的RCS曲线对比图 Fig. 5 Comparsion of the RCS: α=90°, VV Polarization |
|
| 图 6 HH极化下的RCS曲线对比图 Fig. 6 HH Polarization |
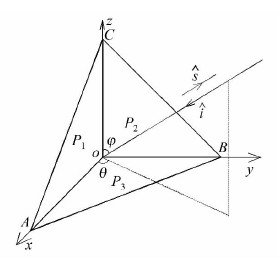
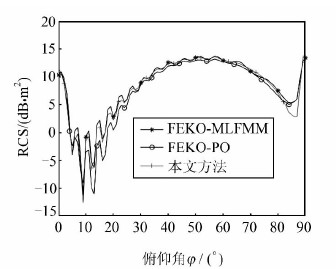
作为SAR辐射定标中最常用的三角形三面角反射器,本文的计算方法同样适用于计算其RCS。对于3个二面角都是90°的三面角反射器,存在着15种反射情况 (P1、P2、P3、P1P2、P1P3、P2P3、P3P2、P3P1、P2P1、P1P2P3、P1P3P2、P2P1P3、P2P3P1、P3P1P2和P3P2P1)。其几何结构如图 7所示,OA=OB=0.2 m,OC=0.22 m,分别与x轴、y轴和z轴重合,ŝ为散射方向,î入射波 与z轴的夹角为φ,其在xoy平面上的投影与x轴夹角为θ,频率为16 GHz。固定方位角θ=45°,俯仰角φ取 0°~90°,其仿真结果如图 8所示,将MLFMM、PO和本文方法的结果进行比对,对应的偏差均值分别是0.3 dB·5m2和-0.61 dB·5m2,可见两者结果基本一致。
|
| 图 7 三面角反射器几何示意 Fig. 7 Geometric Sketch of the Corner Reflector |
|
| 图 8 方位角θ=45°时HH极化下的RCS曲线对比图 Fig. 8 Comparsion of the RCS: θ=45°, HH Polarization |
在验证了本文方法有效性的同时进行了计算时间的比对,以本文描述的两种类型角反射器为例,三条边长分别为OB=OC=OE=1 m,频率为2 GHz的二面角反射器在FEKO中剖分后产生17 162个三角形面元;三条棱长OA=OB=0.2 m,OC=0.22 m,频率为16 GHz的三面角反射器则经剖分后产生34 184个三角面元。由于本文未对平板做任何剖分,因而其RCS计算效率较高,计算时间的比对如表 1所示,本文方法比FEKO中MLFMM和PO算法的计算时间分别缩短了近413倍、4 696倍(二面角反射器)和383倍、9 174倍(三面角反射器),且本文方法占计算机资源极少,而本文所列的FEKO仿真结果均在8核CPU和32 GB内存下运行计算。可见,本文方法大大节约了计算时间,减小了内存消耗,显著地提高了仿真效率。
| 计算时间 | 本文方法 | FEKO | |
| MLFMM | PO | ||
| 二面角反射器 | 2.3 s | 0.264 h | 3 h |
| 三面角反射器 | 3.1 s | 0.33 h | 7.9 h |
采用本文介绍的方法对二面角反射器、三面角反射器等SAR定标体进行RCS计算,通过与文献、电磁仿真软件FEKO的仿真结果比较,可以看出其效果良好,大大缩短了计算时间,为后续通过大量仿真计算优化设计专用于SAR辐射定标的角反射器提供了便利。由于该方法基于射线追迹,因而较适用于电大尺寸平板角形结构多次反射的情形,例如常见的二面角反射器和三面角反射器,但对处于低频区RCS计算误差较大。
| [1] | Chen Erxue, Li Zengyuan, Tian Xin, et al. Terrain Radiometric Correction Model and Its Validation for Space-borne SAR Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3): 322-327 (陈尔学, 李增元, 田昕, 等. 星载 SAR 地形辐射校正模型及其效果评价[J]. 武汉大学学报·信息科学版, 2010, 35(3): 322-327) |
| [2] | Liu Jiayin, You Hongjian, Hong Wen. Modified Orbit Algorithm with Sparse Ground Control Points for Geo-rectification of Space-borne SAR Image[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 262-265(刘佳音, 尤红建, 洪文. 用于星载 SAR 图像几何校正的稀疏控制点修轨方法[J]. 武汉大学学报·信息科学版, 2013, 38(3): 262-265) |
| [3] | Xu Caijun, He Ping, Wen Yangmao, et al. Crustal Deformation Monitoring of Xianshuihe Fault by CR-InSAR[J]. Geomatics and Information Science of Wuhan University, 2012, 37(3): 302-305(许才军, 何平, 温扬茂, 等. 利用 CR-InSAR 技术研究鲜水河断层地壳形变[J]. 武汉大学学报·信息科学版, 2012, 37(3): 302-305) |
| [4] | Ding Yan. Resarch on In-orbit Measurements of SAR Radiometric Calibration Constant and Antenna Pattern by the Marine Field[D]. Beijing: Chinese Academy of Sciences, 2010(丁岩. 利用海洋场在轨测量SAR辐射定标常数和天线方向图方法研究[D]. 北京: 中国科学院研究生院, 2010) |
| [5] | Li Liang, Hong Jun, Ming Feng, et al. An Approach for Ionospheric Effects Correction on Spaceborne SAR Calibration Based on Active Radar Calibrator[J]. Journal of Electronics & Information Technology, 2012, 34(5): 1 096-1 101(李亮, 洪峻, 明峰, 等. 一种基于有源定标器的电离层对星载 SAR 定标影响校正方法[J]. 电子与信息学报, 2012, 34(5): 1 096-1 101) |
| [6] | Freeman A. SAR Calibration: An Overview[J]. Geoscience and Remote Sensing, IEEE Transactions on, 1992, 30(6): 1 107-1 121 |
| [7] | Gray A L, Vachon P W, Livingstone C E, et al. Synthetic Aperture Radar Calibration Using Reference Reflectors[J]. Geoscience and Remote Sensing, IEEE Transactions on, 1990, 28(3): 374-383 |
| [8] | Liu Chen, Sandirasegaram N, English R A, et al. MarCoPola Polarimetric SAR Trial: Signatures of Multiple Vessels with Aligned Operating Conditions[R]. Defence Research and Development Canadaottawa,Ontario, 2005 |
| [9] | Ding Jianjun, Liu Zhiwei, Xu Kan, et al. Application of High Frequency Methods for Scattering Analysis of Electrically Large Objects [J]. Systems Engineering and Electronics, 2010, 32(11): 2 309-2 312(丁建军, 刘志伟, 徐侃, 等. 基于高频方法分析电大尺寸目标的散射[J]. 系统工程与电子技术, 2010, 32(11): 2 309-2 312) |
| [10] | Tao Yubo, Lin Hai, Bao Hujun. GPU-Based Shooting and Bouncing Ray Method for Fast RCS Prediction[J]. Antennas and Propagation, IEEE Transactions on, 2010, 58(2): 494-502 |
| [11] | Wang Yunhua, Zhang Yanmin, Guo Lixin. Investigation of the Scattered Field from a Two-dimensional Dielectric Target Above the Planar Surface with a Guass Beam Incidence[J]. Acta Physica Sinica, 2008, 57(9):5 529-5 535 |
| [12] | Li Qiuming, Vernon R.J. Theoretical and Experimental Investigation of Gaussian Beam Transmission and Reflection by a Dielectric Slab at 110 GHz[J]. Antennas and Propagation, IEEE Transactions on, 2006, 54(11): 3 449-3 457 |
| [13] | Wu Nan, Chen Jiong. Discussion on the RCS Simulation Test of Naval Ships on Water Surface[J]. Chinese Journal of Ship Research, 2012, 7(5): 103-106(吴楠, 陈炯. 舰船目标RCS水面模拟试验及其应用探讨[J]. 中国舰船研究, 2012, 7(5): 103-106) |
| [14] | Gao Fei, Ma Fengguo, Zhang Hongxia, et al. Analysis of Cavity Scattering Based on Complex Rays Method[J]. Chinese Journal of Radio Science, 2000, 15(2): 244-247(高飞, 马凤国, 张红霞, 等. 利用复射线法分析腔体的散射场[J]. 电波科学学报, 2000, 15(2): 244-247) |
| [15] | Gordan W B. Far Field Approximation of the Kirchoff-Helmholtz of Scattered Fields[J]. Antennas and Propagation, IEEE Transactions on, 1975, 23(5): 864-876 |
| [16] | Ruan Yingzheng. Radar Cross Section and Stealth Technology[M]. Beijing: National Defence Industry Press, 1998: 75-76(阮颖铮. 雷达截面与隐身技术[M]. 北京:国防工业出版社,1998: 75-76) |
| [17] | Knott E. RCS Reduction of Dihedral Corners[J]. Antennas and Propagation, IEEE Transactions on, 1977, 25(3): 406-409 |
 2015, Vol. 40
2015, Vol. 40



