文章信息
- 李佳田, 杨琪莉, 罗富丽, 罗辉兰, 林艳
- LI Jiatian, YANG Qili, LUO Fuli, LUO Huilan, LIN Yan
- 线/面Voronoi图的分解合并生成算法
- A Decomposition and Combination Algorithm for Voronoi Diagrams of Polylines and Polygons
- 武汉大学学报·信息科学版, 2015, 40(11): 1545-1550
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1545-1550
- http://dx.doi.org/10.13203/j.whugis20140018
-
文章历史
- 收稿日期: 2014-01-06

2. 中国人民公安大学警务信息工程学院, 北京, 100038
2. Policing Information Technology College, People's Public Security University of China, Beijing 100038, China
Voronoi图是一种关于空间剖分的基础几何结构,它表现为一组生长源同时向四周扩张,直到相遇为止,形成各生长源势力范围的集合[1, 2]。Voronoi图具有空间邻近、空间分布与空间排序等特性,是地理信息科学领域空间建模与分析的有力工具[3]。随着Voronoi图应用的发展,需要线/面生长源Voronoi图参与建模或计算过程。
线/面生长源Voronoi图的生成算法可分为栅格算法与矢量算法两种主要类型,相对于点状生长源之间的等距离边界是其连线的垂直平分线,建立线/面生长源Voronoi图的难点在于线/面图形的不规则所导致的等距离Voronoi边界难以直接计算。例如,两条曲线之间的最短线段(由分属两条曲线的两个最近点)能够在多项式时间内计算得到,并可由最短线段的中点确定等距离Voronoi边界的第一个点,但是,第二个(或后继)等距离点及与之相关联最近点均为未知,不能在多项式时间内计算得出,因此,线/面生源长Voronoi图的构建是NP问题。因此,栅格算法以生长源的栅格空间生长结果来模拟并间接得出Voronoi图,这类算法之间的差异主要是所采用的距离度量方法与生长过程优化方法的不同[4, 5, 6, 7, 8, 9, 10],由于栅格大小与线/面图形分辨率呈比例关系,因此,算法复杂度呈栅格大小的指数形式。矢量算法是用抛物线来部分地代替分解图形间的Voronoi边界,这类算法的主要代表是Quad-Edge算法与Topology-Oriented算法[11, 12, 13],由于抛物线对分解图形等距离边界拟合的要求,目前,矢量算法在生长源类型上是有限制的,主要是以线段与圆弧为代表的较规则形状。
1 分解合并算法 1.1 线/面要素特征点离散表达为了使线/面生长源Voronoi图能够精确地反映生长源总体分布特征及生长源个体局部形态特征,需要考虑生长源之间的距离与构成生长源的结点距离,前者作为Voronoi边界的总体区分 程度量化;而后者是生长源个体Voronoi区域的细致量化。设线/面生长源的原始结点序列形式为:
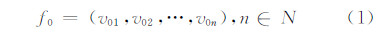
如果是面生长源,则v01=v0n。定义生长源间的最小距离(dF)、生长源结点最小距离(dƒ)为:
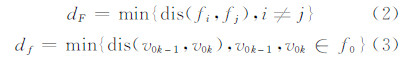
合并dFdƒ,取两者的最小值作为特征值τ:
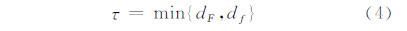
线/面生长源可以看作是以两结点构成的线段序列形式的不规则曲线,以特征值τ为间距,对线段进行新结点的线性插入,线/面生长源的结点序列形式描述为:
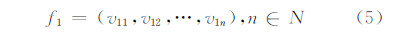
可以得出,原始结点与新插入结点是生长源边界的一种离散表达,使得结点间线段距离小于等于τ,这里称原结点与新插入结点为生长源在特征值τ条件下的特征点。
1.2 最近特征点对如果以特征点近似表达生长源,那么生长源不规则曲线间的最短距离可转化为特征点到曲线的最短距离,即通过计算特征点的曲线最近点,进而可以得到等距离点来构建Voronoi边界。线/面生长源由线段构成,那么特征点到不规则曲线的最短距离转化为特征点到线段的最短距离。
考虑线段为向量形式v1iv1i+1,则只需计算向量v1ip在向量v1iv1i+1上的投影v1ic:
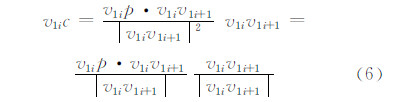
式中,‖是向量的长度;•是向量的内积,并且v1ip•v1iv1i+1=|v1ip||v1iv1i+1|cosθ,θ为向量v1ip与向量v1iv1i+1之间的夹角;v1iv1i+1/|v1iv1i+1|是v1iv1i+1方向上的单位向量。因此,v1ip•v1iv1i+1/|v1iv1i+1|=|v1ip|cosθ即为图 1中线段v1ic的长 度值,不具有方向性,并且此值是向量v1iv1i+1/|v1iv1i+1|方向上的长度,即新向量v1ic,也是向量v1ip在v1iv1i+1方向上的投影。令c为投影点,并设
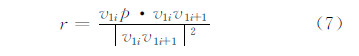

|
| 图 1 特征点在线段的投影与最短距离 Fig. 1 Projection and Shortest Distance Between Feature Points and Line Segment |
则由向量的方向性可知,图 1(a)中,有0 < r < 1;图 1(b)中,有r≥1;图 1(c)中,则r≤0。更进一步地,根据r值的不同,特征点到线段的最短距离dmin为:

得到特征点p在线段v1iv1i+1的最近点p′构成最近特征点对(p,p′):
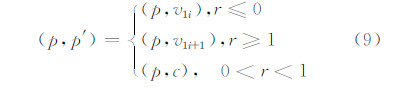
给定两条不规则曲线ƒ11、ƒ12代表线/面生长源,首先,以ƒ11的特征点在ƒ12上分别计算得到与之相关联的最近点,并用最近点再次对ƒ12离散;反之,交叉计算,对ƒ11再次离散。计算最短距离时,可先根据式(5)得到特征点之间的距离变化状态,即当某一线段的结点距离由大变小转为由小变大时,认为该线段包含最近点,进而根据式(9)得到最近点。交叉最近点再次离散化后,生长源描述如下:
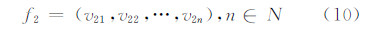
线/面生长源被表达为特征值τ 与最近特征点对的离散形式。因为最近特征点对是建立在特征值离散的基础之上,直接的做法是用最近特征点对连线的中点作为Voronoi边界结点,但是,这样做的前提条件是每对最近特征点必须在Voronoi边界表达中出现。
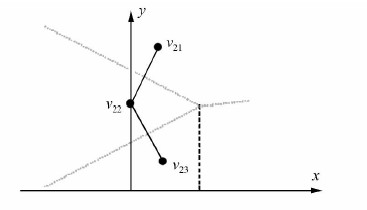
某一最近特征点对能否对Voronoi边界表达起到作用,受到当前特征点与其邻近分布特征点的位置关系制约。如图 2所示,存在v21、v22与v23三个特征点及它们的Voronoi子区域。如果以x 轴正方向为考察方向,当距离大于d时,v22特征点不再被表达,而是被v21与v23特征点的Voronoi子区域所代替,与这个现象等价的是,当Voronoi边界位于与v22最近特征点对构成的线段中点右侧时,Voronoi边界由v21与v23所决定,而v22被隐含。此时,由于Voronoi边界为所求,即是未知,难以直接计算哪些最近特征点被隐含。如果用特征点的Voronoi子区域来近似线/面生长源的Voronoi子区域,首先,被隐含的特征点由于没有参与Voronoi边界表达可直接得出;其次,如果最 近特征点对参与Voronoi边界表达,根据Voronoi图的定义,最近特征点对的Voronoi子区域的交集为一条线段(或一点),并且线段上的任意点必然是最近特征点对的等距离点,即其属于Voronoi边界。因此,自然的做法是用线/面生长源特征点的Voronoi子区域并集形式描述线/面生长源的Voronoi子区域,即
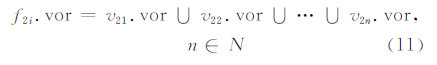
|
| 图 2 特征点与Voronoi边界表达关系 Fig. 2 Expression Relationship Between Feature Points and Voronoi Boundary |
随着特征值τ的减小,特征点与最近特征点对数量呈线性增长趋势,从生长结果分析,即是对线/面生长源或线/面生长源Voronoi子区域的表达越来越精确。假设在固定范围的二维空间域内,以多个递减τ值做多次的线/面生长源离散,随着τ值的减小,特征点逐渐增多,以特征点Voronoi子区域并集形式表达的线/面生长源Voronoi子区域会越来越精确。因为空间域固定,使得某些线/面生长源的Voronoi子区域的前后两次τ值计算结果表现为正面积差,而某些线/面生长源会出现负面积差。
设有τ1、τ2两次生长源离散,并且τ1>τ2,则用面积差分形式度量线/面生长源个体Voronoi子区域的面积变化,即
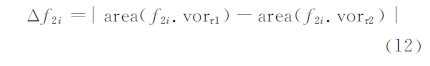
式中,| |为面积差的绝对值。生长源总数为M,由式(13)可得出线/面生长源总体的面积差分均值:
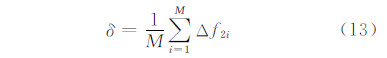
设δ≤ε(ε 为实数值)为算法精度条件,则可有选择性地对部分线/面生长源迭代离散,当生长源个体Voronoi区域的面积变化小于总体变化均值δ时,认为其没有对Voronoi子区域的面积差异变化产生主要影响,因此,选择生长源进行迭代离散的条件如下:
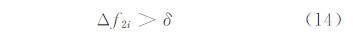
迭代离散后,需要根据式(12)、式(13)重新计算δ值,并以其作为生长源新的离散过程选择依据。
给出生长源的数据结构feaGor
struct feaGor
{
integer fid;
pointArray feapoints;
boolean discrate = true;
polygon vor;
double areaf = -1;
double areat = -1;
}
其中,fid为生长源的唯一标识,整数类型;feapoints代表生长源的特征点,为point < fid,x,y,vor>类型数组;而discrate为布尔量,代表生长源是否需要继续再次迭代离散操作,其初始值为真;vor为生长源的Voronoi子区域,为polygon类型;areaf与areat为浮点类型,用于记录生长源Voronoi子区域面积值,初始化为-1。
综上,给出算法过程描述如下:
算法输入:线/面生长源集合F,精度值ε
算法输出:线/面生长源Voronoi图
1) 根据式(2)、式(3),遍历集合F,计算得出dF、dƒ值,取两者的最小值同时赋予τ的初始值与当前值,τori,τcur←min{dF,df};
2) 对于∀ƒ∈F,如果f.discrate=true,以τcur值对其离散为特征点,F1←ƒ1,形成生长源集合F1;
3) 对于∀ƒ1∈F1,根据式(9),对于∀v1i∈ƒ1,计算v1i的最近特征点v1j,并进行生长源的交叉离散,F2←ƒ2,形成生长源集合F2;
4) 以F2的特征点,构建特征点的Voronoi图;
5) 依据式(11),对于∀ƒ2∈F2,以特征点fid值相等为条件,合并ƒ2.feapoints的Voronoi子区域为ƒ2.vor,计算得出ƒ2.vor面积值areavor;
6) 如果ƒ2.areaf ≠ -1,ƒ2.areaf ← areavor,或者,ƒ2.areat ≠ -1,ƒ2.areat ← areavor;否则,ƒ2.areaf ← ƒ2.areat,ƒ2.areat ← areavor;
7) 如果τori=τcur,那么τcur← τcur/2,则返回步骤2);
(1) 对于∀ƒ2∈F2,依据式(12)、式(13),计算Δƒ2←|ƒ2._areaf-ƒ2.areat|与δ值;
(2) 如果δ小于ε,进行步骤8);
(3) 如果Δƒ2大于δ,置ƒ2.diacrate = false,否则,置ƒ2.diacrate = true,返回步骤(1);
(4) 置τcur←τcur/2,F←NULL,F←F2,返回步骤2);
8) 对于∀ƒ2∈F2,输出ƒ2.vor;
9) 算法结束。
2 算例与分析设生长源数量为n,生长源初始平均结点数为m,分析算法各步骤的时间复杂度,遍历计算dF、dƒ值,有O(mn);以τ值对生长源离散操作1次,有O(n);生长源之间交叉建立最近特征点对,有O(mn);构建特征点Voronoi图及合并,有O(mn);设迭代c次,算法达到精度要求,则有c(O(n)+O(mn)+O(mn));相加并化简,得出分解合并算法的时间复杂度为O(mn)。对于生长源数量较大情况,有n≈m,算法时间复杂度可进一步化简为O(n2)。
栅格距离变换Voronoi图生成算法是目前公认的高精确度Voronoi图生成算法,为了进行算法有效性分析,本文采用栅格距离变换Voronoi图生成算法[14]的结果作为对照。实验数据为线状类型河流,平面坐标系并经旋转与比例尺缩小变换,固定实验区域大小为3 231 m×2 085 m,面积为6 736 635 m2。设栅格大小为3 m×3 m,根据生长源的fid值,赋予生长源为不同颜色,栅格化实验区域为695行×1 077列、3通道、8位深度的RGB位图,并设置背景颜色为白色。对于任一个栅格,如果其颜色RGB值为(255,255,255),则代表背景;否则,代表生长源。以逐行扫描的方式遍历栅格,如果其为背景,则对其进行相对于生长源的栅格距离计算,此处,以欧氏平面距离作为距离度量方法,赋予栅格颜色为距离最小值所对应的生长源颜色。栅格距离变换算法所生成的Voronoi图结果如图 3所示。
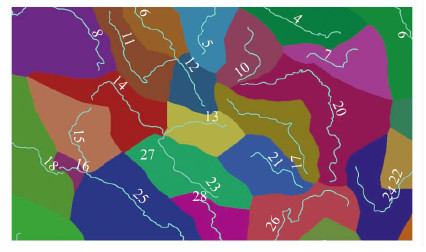
|
| 图 3 线状要素的栅格距离变换Voronoi图 Fig. 3 Voronoi Diagram of Polylines by Raster Algorithm |
以同样的数据进行本文算法,计算得到初始τ值为320,并以间隔值20递减至60,逐步观察δ值的变化情况。如图 4所示,经过4次递减后,δ快速地降至100 000以下,说明前期随着最近特征点对数量的增加,生长源个体的Voronoi子区域快速调整,并且差异变化相对较大;当τ值在240~160之间时,δ值线性递减至小于20 000,生长源个体的Voronoi子区域调整至基本稳定状态;当τ小于160时,δ同样呈减小趋势,生长源个体的Voronoi子区域随着特征点的增多变化不明显,说明在做局部微小调整;直至τ值为60,此时,δ值为9 530,趋于稳定,与栅格算法的结果面积差异约为1 059个栅格大小,占实验区域总面积的0.14%。需要说明的是,实际构建过程中,可设τ值为1/2倍递减,以使算法经过少数迭代次数快速达到精度要求。

|
|
图 4 |
取τ为240、180、120、60等4种情况所生成的线生长源Voronoi图(线状)与栅格算法生成的Voronoi图(填充)对比,差异较为显著的区域分别用矩形线框标出,如图 5所示。当τ为240时,本文算法结果与栅格算法结果差异较大,标注区域1中,最近特征点对形成的等距离边界位于Voronoi边界的两侧,而在区域2与区域3中,等距离边界主要位于Voronoi边界的一侧,以上现象出现的原因是由于生长源位置分布的随机性所导致的等距离边界由少数最近特征点对决定。例如,区域1中的Voronoi边界由14、15号生长源生成,由于14与15号生长源的边界邻近端呈共线位置分布,使得Voronoi边界由少数几对最近特征点对决定,因此,造成等距离边界向两侧偏移;而在区域2中,Voronoi边界由12、13号生长源生成,可以看出,12号与13号生长源边界邻近端呈垂直位置分布,虽然所形成的最近特征点对数量较多,但主要是由12号生长源单一特征点所构成,因此,会出现等距离边界向一侧位置偏移;而在区域3中,Voronoi边界由13、21、23号生长源生成,它们之间的最近特征点对的构成是区域2中情况的复合,即21号生长源的特征点单一,因此,等距离边界向21号生长源位置偏移。当τ为180时,相对于图 5(a),区域1、2、3中的等距离边界与Voronoi边界差异明显减小,区域1中相对变化明显,说明特征值减少对邻近端共线情况改善更加显著;当τ为120时,等距离边界与Voronoi边界基本粘合;当τ为60时,等距离边界仅在局部有微小改正。由此可见,随着参数τ的减小,本文算法结果与栅格算法结果差异逐渐减小,在实际应用中可以根据精度要求选取合适的τ值。
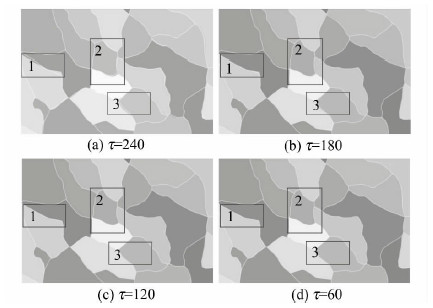
|
| 图 5 本文算法与距离变换栅格算法的比较 Fig. 5 Comparison Between Our Algorithm and the Raster Algorithm |
图 6为云南楚雄市数据,共包含1 500个面生长源(居民地)、102个线生长源(道路)及3 103个点生长源(兴趣点),算法经5次迭代计算的局部结果。
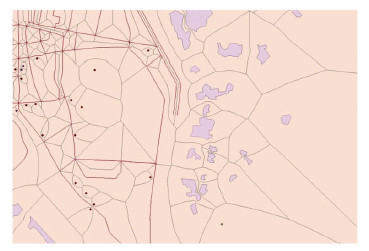
|
| 图 6 云南省楚雄市局部居民地、道路与兴趣点Voronoi图,算法5次迭代结算结果 Fig. 6 Voronoi Diagram of the Local Settlements,Roads and POIs in Chuxiong City, Yunnan, by Five Iterations of Our Algorithm |
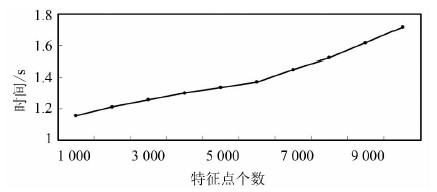
本文算法将线/面生长源离散为特征点,通过构建、合并特征点的Voronoi图完成线/面Voronoi图的构建,其本质上是点的Voronoi图的生成与合并,故算法效率与特征点个数相关。采用图 8中的数据,从10 000个特征点起依次递增10 000个特征点作为实验数据集合,算法耗费时间如图 7所示,可以看出,在处理大数据量时本文算法依旧具有较高的效率。
|
| 图 7 本文算法计算效率 Fig. 7 Algorithm Computational Efficiency |
本文针对线/面生长源Voronoi图生成问题,提出了生长源节点序列概念,以特征值描述下的特征点来表达线/面生长源,以最近特征点对Voronoi子区域的交来近似线/面生长源等距离边界,使用线/面生长源Voronoi区域差分方法,有选择地对部分生长源迭代离散,调整其Voronoi子区域,通过合并特征点Voronoi子区域完成线/面Voronoi图的构建。实验验证,本文算法是有效的,生成Voronoi图的精度与选取的离散距离相关,能够满足不同精度要求,具有较高的效率。
不足之处总结为以下两点:(1) 虽然算法可以选择将部分生长源置入迭代离散过程以提高计算效率,但从实验分析得出,等距离边界的调整只受部分最近特征点对影响,后继工作中,可将构建等距离边界的最近特征点对类型并入考虑;(2) 随着栅格大小变化,对照实验所采用的传统栅格距离变换Voronoi算法生成的Voronoi图精度也是变化的,由于栅格算法复杂度过高,受实验条件的限制,没有给出特征值与栅格大小一致变化情况之下的两种算法结果精度对比。
| [1] | Gold C. Review: Spatial Tessellation-Concepts and Applications of Voronoi Diagrams [J]. International Journal of Geographical Information Science, 1994, 8(2): 237-238 |
| [2] | Okabe A, Boots B,Sugihare K, et al. Spatial tessellations: Concepts nd Applications of Voronoi Diagrams [M]. New York: Wiley, 2000 |
| [3] | Chen Jun. Voronoi-based Dynamic Spatial Data Model [M]. Beijing: Publishing House of Surveying and Mapping, 2002(陈军. Voronoi动态空间数据模型[M]. 北京: 测绘出版社, 2002) |
| [4] | Yan Haowen, Wang Bangsong. A MWVD-based Algorithm for Point Cluster Generalization [J]. Geomatics and Information Science of Wuhan Univers, 2013, 38(9): 1 088-1 091 (闫浩文, 王邦松. 地图点群综合的加权Voronoi算法[J]. 武汉大学学报·信息科学版, 2013, 38(9): 1 088-1 091) |
| [5] | Shen Jing, Liu Jiping, Lin Xiangguo, et al. A Method for Delaunay Triangulation by Integration of Distance Transformation and Region Adjacency Graphics [J]. Geomatics and Information Science of Wuhan Univers, 2012, 37(8): 1 000-1 003 (沈晶, 刘纪平, 林祥国, 等. 集成距离变换和区域邻接图生成Delaunay三角网的方法研究[J]. 武汉大学学报·信息科学版, 2012, 37(8): 1 000-1 003) |
| [6] | Wang Xinsheng, Liu Jiyuan, Zhuang Dafang, et al. New Raster-Based Method for Constructing Voronoi Diagrams [J]. Journal of China University of Mining & Technology, 2003, 32(3): 293-296 (王新生, 刘纪远, 庄大方, 等. 一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报, 2003, 32(3): 293-296) |
| [7] | Xie Shunping, Wang Jiecheng, Feng Xuezhi, et al. Algorithm for Constructing Voronoi Diagram of Planar Points Based on Approximating and Extracting Vertices [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 436-442 (谢顺平, 王结臣, 冯学智, 等. 基于结点逼近提取的平面点集Voronoi图构建算法[J]. 测绘学报, 2007, 36(4): 436-442) |
| [8] | Zhao Renliang. Voronoi Methods for Computing Spatial Relations in GIS [M]. Beijing: Publishing House of Surveying and Mapping, 2006 (赵仁亮. 基于Voronoi图的GIS空间关系计算[M]. 北京: 测绘出版社, 2006) |
| [9] | Schueller A. A Nearest Neighbor Sweep Circle Algorithm for Computing Discrete Voronoi Tessellations [J]. Journal of Mathematical Analysis and Applications, 2007, 336(2): 1 018-1 025 |
| [10] | Dong Pinliang. Generating and Updating Multiplicatively Weighted Voronoi Diagrams for Point, Line and Polygon Features in GIS [J]. Computer & Geosciences, 2008, 34(4): 411-421 |
| [11] | Guibas L, Stolfi J. Primitives for the Manipulation of General Subdivisions and the Computation of Voronoi Diagrams [J]. ACM Transactions on Graphics, 1985, 4(2): 74-123 |
| [12] | Imai T, Sugihara K. A Failure-Free Algorithm for Constructing Voronoi Diagrams of Line Segments [J]. Information Processing Society of Japan, 1994, 35(10): 1 966-1 977 |
| [13] | Held M, Huber S. Topology-Oriented Incremental Computation of Voronoi Diagrams of Circular Arcs and Straight-Line Segments [J]. Computer-Aided Design, 2009, 41(5): 327-338 |
| [14] | Hu Peng, You Lian, Yang Chuanyong, et al. Map Algebra [M]. Wuhan: Wuhan University Press, 2006 (胡鹏, 游涟, 杨传勇, 等. 地图代数[M]. 武汉: 武汉大学出版社, 2006) |
 2015, Vol. 40
2015, Vol. 40


