文章信息
- 余旺盛, 田孝华, 侯志强, 陈校平
- YU Wangsheng, TIAN Xiaohua, HOU Zhiqiang, CHEN Xiaoping
- 基于OLDM与贝叶斯估计的鲁棒视觉跟踪
- Robust Visual Tracking Based on OLDM and Bayesian Estimation
- 武汉大学学报·信息科学版, 2015, 40(11): 1539-1544
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1539-1544
- http://dx.doi.org/10.13203/j.whugis20130535
-
文章历史
- 收稿日期: 2014-04-25

视觉跟踪是计算机视觉领域研究的热点和难点问题。当目标的表观特征在跟踪的过程中发生变化时,跟踪的稳定性与精度均会受到影响。因此,构建一个能够适应目标表观特征变化的模型是解决问题的关键之一。传统的跟踪算法主要利用生成式模型(generative model)对目标进行建模,如模板匹配跟踪、Mean Shift跟踪以及粒子滤波跟踪等利用模板的全局统计信息构建生成式模型。Adam等[1]提出的Fragments\|based算法,Yang等[2]提出的特征包(BoF)跟踪,Ross等[3]提出的增量主成分分析(IVT)算法以及近年来广受关注的基于稀疏表示的目标跟踪算法[4]等,均从不同的特征子空间来构建生成式模型。Oron等[5]利用局部的颜色以及结构分布来构建目标模型,对尺度以及背景干扰具有一定的鲁棒性,但容易受到光照变化影响。生成式模型的缺点是仅仅利用了目标的前景特征(正样本)。研究表明[6, 7],在目标检测时,目标周围背景特征(负样本)的合理利用能够大大提高目标检测算法的性能。基于判别式模型(discriminative model)的目标跟踪算法正是充分利用了大量的负样本,才提高了跟踪中目标检测的成功率。判别式模型通常需要通过在线学习从标记的正负样本中学习最能区分正负样本的特征,进而通过构建分类器来完成目标跟踪,如Zhang等[8]提出的压缩跟踪(compressive tracking,CT)等。Wu等[9]对近10年来出现的在线视觉跟踪算法进行了系统总结和实验评估。
文献[10]提出利用超像素区域的特征聚类分析来构建目标的判别式模型,提高了目标在背景区域的可区分度,增强了算法对目标表观变化的适应性。在此基础上,本文通过引入分水岭算法获取训练样本,借助聚类算法构建在线学习判别式模型,然后通过设计模型更新策略,在贝叶斯框架下提出了一种基于在线学习的鲁棒视觉跟踪算法。
1 在线学习判别式模型(OLDM) 1.1 建模思路设 {s1,…,si,…,sn}为分割得到的训练样本,其中样本si由落入该区域的所有像素构成,记为{ei1,…,eij,…,eini},像素对应的初始标记为{li1,…,lij,…,lini},通过如下方法获取:

式中,ƒg为初始标定的目标区域;bg 为目标所处的背景区域。OLDM建模的思路为:通过对一定数量的训练样本进行特征聚类并构建判别函数,由判别函数确定聚类结果的标记后,反向标记训练样本,从而减小由像素标记直接对训练样本进行分类判别所引入的标记误差。
首先对训练样本进行特征聚类得到{c1,…,ck,…,cm},然后构建类ck的判别函数如下:
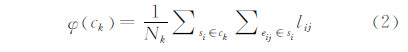
式中,Nk为类ck中所有训练样本包含的像素个数的总和。此时,ck对应的标记为:
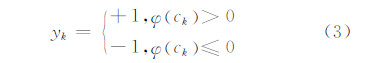
当输入测试样本{t1,…,tj,…,tn′}时,构建各测试样本的判别函数如下:
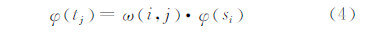
式中,si为测试样本tj在特征空间的最近邻训练样本;φ si 为si所隶属的特征聚类的函数判别值;ω(i,j)为由特征距离与空间距离共同决定的权重系数,其计算公式为:

式中,d1(si,tj)为样本间的空间距离;d2(si,tj)为样本之间的特征距离;λ1与λ2为归一化参数。
当所有测试样本的判别值计算出来后,可得测试样本tj的标准化判别值为:
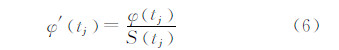
式中,S(tj)为样本tj的面积,标准化判别值的大小位于[-1,1]之间。此时,属于相同测试样本的像素拥有与所属样本相同的标准化判别值:
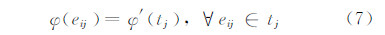
像素的标准化判别值表征该像素属于目标前景或者背景的可能性大小。由像素的标准化判别值即可计算目标的似然分布,然后通过贝叶斯估计算法实现目标的跟踪。
1.3 模型更新设训练样本的样本容量为R,模型更新的具体思路为:将训练样本排列成队列,当前帧跟踪完成后,当队列长度小于样本容量时,需要从当前跟踪结果的测试样本中选取满足一定条件的样本对训练样本进行补充;当队列长度超过样本容量时,在补充新的训练样本时需要等量删除队列中的旧样本。旧样本的确定方法:当目标未发生遮挡时,样本队列尾部的训练样本最早进入队列,对当前目标的描述能力相对最弱,故将其确定为旧样本;当目标出现遮挡时,最早进入队列的样本保留了目标的基本特征,而新引入的样本包含了目标可能发生的变化,此时将队列中间位置的训练样本确定为旧样本,既保证了模型对遮挡变化的鲁棒性,又增强了模型对目标新特征的学习能力。
跟踪过程中,设定训练样本的样本容量为初始样本数量的10倍,每两帧对训练样本进行一次更新,在未发生遮挡时每5帧对目标模型进行一次更新。更新的具体操作与目标初始模型的构建类似,只是训练样本的数目发生了变化。
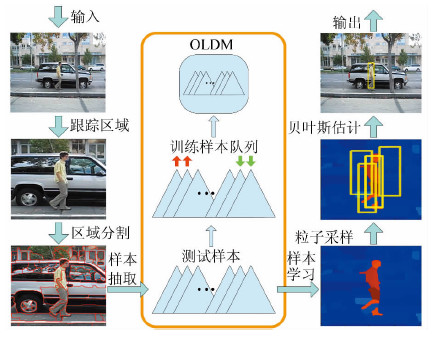
2 跟踪算法介绍根据所提出的OLDM,本文结合贝叶斯估计来实现目标跟踪。跟踪过程如图 1所示。
|
| 图 1 本文算法跟踪示意图 Fig. 1 Demonstration of the Tracking Flow |
给定目标初始状态X1= (x1,y1,h1,w1 ),其中 (x1,y1) 为目标的中心位置,(h1,w1) 为目标区域的大小。设定目标所处的背景区域为以 (x1,y1)为中心,3倍于目标区域大小的环形区域。由目标区域和背景区域共同构成大小为( h′1,w′1) 的跟踪区域,即有h′1=2h1,w′1=2w1。目标区域的像素标记为“1”,背景区域的像素标记为“-1”。模型初始化的关键步骤如下。
1) 样本抽取。本文采用文献[11]提出的自适应标记分水岭算法进行区域分割。利用分割所得区域建立训练样本集合,记为{s1,…,si,…,sn},对每个样本进行特征描述,即ƒ si = sic ,sih ,其中sic 为第i个样本的中心位置,sih 为第i个样本在HSI空间的颜色直方图。
2) 特征聚类。采用Mean Shift算法[12]对训练样本{s1,…,si,…,sn}在HSI空间进行直方图聚类,聚类所得的结果记为{c1,…,ck,…,cm}。聚类后,颜色特征相似的样本被聚成相同的类,减小了像素初始标记误差对后续处理的影响。
3) 样本标记。确定每一个聚类包含和样本以及像素,根据式(2)计算聚类的判别值大小,值越大,表明该聚类为目标前景的概率越大,反之表明该聚类为背景的概率越大。根据判别值的大小,利用式(3)确定聚类的标记,并反向确定构成聚类的样本以及像素的标记和判别值。当所有像素的判别值确定后,初始模型构建完成。
2.2 计算似然分布在t时刻输入视频帧时,根据上一时刻的目标状态Xt-1确定当前的跟踪区域,则似然分布估计的关键步骤如下。
1) 样本抽取。抽取当前帧的测试样本{t1,…,tj,…,tn′},并对所有测试样本进行特征描述,其中第j个样本的特征记为 (tjc ,tjh)。
2) 样本学习。利用式(4)和式(5)计算所有测试样本的判别值。式(5)中的空间距离度量公式具体如下:
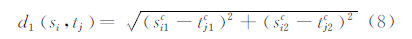
特征距离度量公式为:
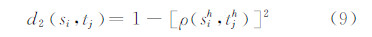
式中,ρ (sih ,tjh)为巴氏系数,其计算公式为:
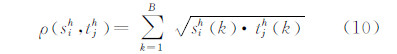
3) 确定似然。根据样本判别结果,确定跟踪区域所有像素的判别值,通过对像素的判别值求和确定跟踪区域的似然概率。跟踪区域外其他像素的判别值赋值为-1。
2.3 最大后验概率估计根据上一时刻的目标状态 Xt-1和目标的状态转移模型,在状态空间内利用高斯随机采样的方法进行离散采样,得到一组粒子{Xt (k) },k=1,2,…,N。状态转移模型参数用对角阵表示,记为diag (x,y,h,w ),其中x,y,h,w分别表示目标的空间位置和尺度变化的幅度,单位为像素。对于第k个粒子,确定其转移概率p(Xt(k)丨Xt-1 ),结合贝叶斯估计公式计算该粒子的后验概率如下:
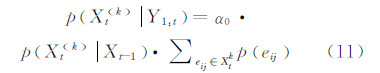
式中,α0为归一化参数,保证后验概率的取值范围在 0,1 之间。求和项表示的是第k个粒子的似然值。
式(11)无法体现尺度变化对后验概率取值的影响,通过增加“尺度适应因子”得到如下公式:
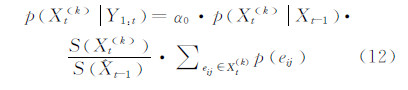
式中,S(Xt(k) )为粒子Xt(k) 的面积。当粒子包含的前景像素越多时,粒子面积越大,粒子对应的后验概率值越大;当粒子包含的背景像素越多时,粒子面积越大,粒子对应的后验概率值越小。因此,尺度适应因子能够增大真实反映目标状态的粒子的后验概率,从而达到尺度只适应的效果。
根据所得的概率分布密度,得到目标的最大后验概率估计为:
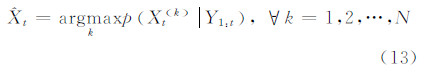
首先根据跟踪结果的变化判断当前帧是否发生遮挡,遮挡判断因子计算如下:
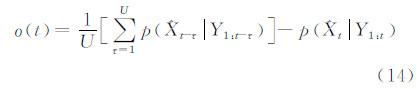
式中,参数 U为训练样本队列所涉及的视频帧的长度,本文中根据每帧包含的训练样本数量变化,U的取值为9到11之间。
当遮挡判断因子满足如下条件时,判断为遮挡发生:

式中,θ0为阈值参数,经验取值为[0.45,0.55]之间。
总结模型更新的策略如下:
1) 当未发生遮挡时:达到训练样本更新条件后,在训练样本队列首部补充新的训练样本,同时等量删除队列尾部的训练样本;达到模型更新的条件后,对训练样本进行聚类分析更新目标模型。
2) 当发生遮挡时:达到训练样本更新条件后,在队列首部补充新的训练样本,同时等量删除队列中部的训练样本;暂停目标模型更新。
3 实验结果与分析为验证所提算法的有效性,在公开的在线目标跟踪算法测试平台下对本文算法进行了一系列的测试,目标的表观变化类型包括尺度变化、部分遮挡、光照变化以及姿态变化等,并与具有代表性的参考算法进行跟踪对比与性能分析。仿真测试的硬件平台为主频3.29 GHz,内存3.24 GB的个人计算机,软件平台为Matlab2011。
3.1 参数设置1) 区域分割的阈值参数。区域分割时,采用标记分水岭算法,扩展最小变化(H\|minma)参数设定为1~10之间,根据跟踪目标的大小,参数略有调整。
2) 训练样本特征聚类时的带宽。对训练样本进行Mean Shift聚类时,聚类的特征对归一化的直方图特征,带宽参数规定在0.15~0.25之间,本文实验均取为0.2。
3) 遮挡判断的阈值。遮挡判断参数设置在0.45~0.55之间能够取得相对更为理想的结果,本文实验均取为0.5。
4) 训练样本更新频率。本文实验中每两帧对训练样本进行更新一次。
5) 模型更新频率。在无遮挡出现的情况下,每5帧对模型进行一次更新。
6) 贝叶斯估计时的采样粒子数。采样粒子数根据跟踪精度要求设置在200~500之间,本文所有实验均设为300。
7) 状态转移模型参数。采用经验赋值法,具体取值将在后续内容中给出。
所选取的参考算法依次为CT[8](2012)、LOT[5](2012)以及SPT[4](2013),参考算法的代码由原文献提供,参数沿用默认设置。
3.2 实验结果针对本文提出的算法,选取了Online Object Tracking Benchmark跟踪平台[9]提供的4组视频序列(“Singer1”,“David3”,“Trellis”和“Bolt”)进行了仿真实验,目标的表观变化类型涉及尺度变化,遮挡变化,光照变化以及非刚性形变等。实验中4组视频的状态转移模型参数设置依次为:diag 15,15,4,4 、diag 8,8,0,0 、diag 8,8,2,2 、diag 8,8,1,1 。实验比较如图 2所示。

|
| 图 2 4种算法跟踪结果比较 Fig. 2 Comparison of Four Algorithms Tracking Results |
1) 尺度变化。 “Singer1”序列中,由于摄像机的拉伸以及环境光照的变化,目标的表观特征以及所处背景环境均发生了较大变化。本文算法基本能够适应目标的尺度变化,取得相对稳定的跟踪结果。参考算法中,CT和SPT算法受光照变化的影响较小,但未能适应目标的尺度变化,LOT算法则受光照变化干扰较大,这是因为LOT算法依赖于局部颜色分布,而这一分部对光照比较敏感。
2) 遮挡变化。“David3”序列中,跟踪目标出现两次严重遮挡,在遮挡发生前后,本文算法和LOT算法自始至终均能对目标进行有效跟踪。CT算法和SPT算法则在第一次严重遮挡(第84帧左右)后便发生跟踪漂移,导致性能明显下降。
3) 光照变化。“Singer1”序列出现了距离的全局光照变化,LOT算法收到的干扰最大,本文算法以及其余两种参考算法均对全局光照具有一定的鲁棒性,跟踪未发生漂移。“Trellis”序列中包含局部的非线性光照变化,跟踪的难度较大,此时仅本文算法对局部光照的变化保持一定鲁棒性,其余算法在跟踪过程中均出现不同程度的跟踪偏差。
4) 非刚性形变。“Bolt”序列包含目标的非刚性形变、尺度变化、复杂背景干扰、目标快速运动等多种变化,对跟踪算法提出了较大的挑战。CT算法和SPT算法从一开始就由于复杂的背景干扰而丢失了目标,LOT算法在刚开始时保持了较高的跟踪精度,但随着颜色和结构均相似的目标出现,算法发生偏移,最终导致跟踪失败。本文算法则成功完成了所有视频帧的跟踪。
3.3 性能分析 本文采用中心位置误差(center location error)对跟踪精度进行定量分析与评价。中心位置误差定义为每一帧中算法跟踪结果的中心位置与Ground Truth的中心位置之间的欧氏距离,计算公式如下: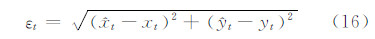
式中,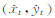 为第t帧跟踪所得的中心位置坐标; (xt,yt)为相应的Ground Truth标定的中心位置坐标。中心位置误差越小,表明算法跟踪的精度越高。
为第t帧跟踪所得的中心位置坐标; (xt,yt)为相应的Ground Truth标定的中心位置坐标。中心位置误差越小,表明算法跟踪的精度越高。
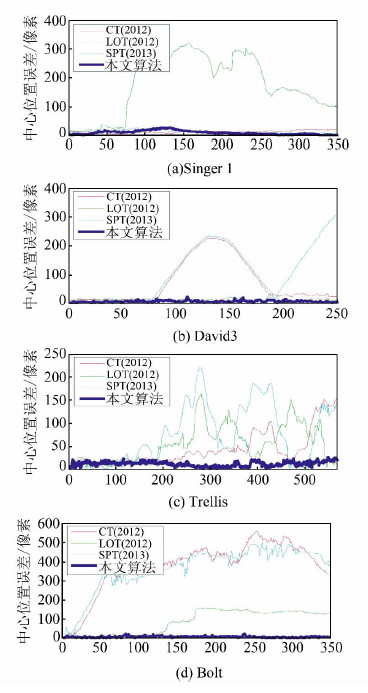
实验中,分别计算了本文算法与参考算法的中心位置误差,详细比较如图 3所示。由图 3可以看出,CT算法和SPT算法的性能曲线仅在“Singer1”序列中较为稳定,LOT算法仅在“David3”序列中的曲线较为平缓,而本文算法在大多数视频中均取得了相对更小的中心位置误差。
|
| 图 3 4种算法的中心位置误差比较 Fig. 3 Comparison of Four Algorithms of Center Location Error Results |
为进一步对跟踪的精度和稳定性进行统计分析,计算中心位置误差的均值(Mean)和均方误差(mean square error,MSE)如下:
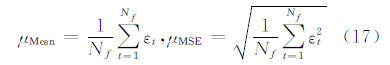
表 1给出了对中心位置误差的统计分析结果比较。 在中心位置误差均值比较中,本文算法除了在“Singer1”序列中的结果不是最优(表中粗体所示)以外,在其余视频中均得到最优结果。统计结果表明本文算法的跟踪精度更高,性能更加稳定。
需要指出的是,在本文给定的实验环境下,CT算法和SPT算法可以实时运行,而LOT算法的平均跟踪速率为0.7帧/s。本文算法跟踪的平均速率为3.2帧/s,实时性能不及CT算法和SPT算法,但较LOT算法有一定优势。
4 结 语本文提出了对目标表观特征自适应性能良好的OLDM,在此基础上,结合贝叶斯估计理论提出了一种能够处理目标复杂表观变化的跟踪算法。相较于传统的目标模型,OLDM对目标复杂表观特征变化的适应能力要强,跟踪的鲁棒性和稳定性也明显提升。本文对OLDM以及所提跟踪算法进行了详细介绍,并在标准数据平台下进行了仿真测试。实验结果表明,本文算法能够有效应对目标的尺度、遮挡、光照变化以及非刚性形变,跟踪的精度和跟踪稳定性较参考算法均有一定提高。
| [1] | Adam A, Rivlin E, Shimshoni I. Robust Fragment-Based Tracking Using Integral Histogram [C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, USA, 2008 |
| [2] | Yang F, Lu H, Chen Y. Bag of Feature Tracking[C]. Proceedings of the 20th International Conference on Pattern Recognition (ICPR),Istanbul, Turkey, 2010 |
| [3] | Ross D, Lim J, Lin R, et al. Incremental Learning for Robust Visual Tracking [J]. International Journal of Computer Vision, 2008, 77(1): 125-141 |
| [4] | Wang D, Lu H, Yang M. Online Object Tracking with Sparse Prototypes [J]. IEEE Transactions on Image Processing, 2013, 22 (1): 314-325 |
| [5] | Oron S, Bar-Hillel A, Levi D,et al. Locally Orderless Tracking [C]. Proceedings of the 25th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, USA, 2012 |
| [6] | Du B, Zhang L. Target Detection Based on a Dynamic Subspace [J]. Pattern Recognition, 2014, 47(1): 344-358 |
| [7] | Du B, Zhang L, Tao D,et al. Unsupervised Transfer Learning for Target Detection from Hyperspectral Images [J]. Neurocomputing, 2013, 120: 72-82 |
| [8] | Zhang K, Zhang L, Yang M. Real-time Compressive Tracking [C]. Proceedings of the 7th European Conference on Computer Vision (ECCV),Berlin, Germany, 2012 |
| [9] | Wu Y, Lim J, Yang M H. Online Object Tracking: A Benchmark [C]. Proceedings of the 26th IEEE Conference on Computer Vision and Pattern Recognition (CVPR),Portland, USA, 2013 |
| [10] | Wang S, Lu H, Yang F, et al. Superpixel Tracking [C]. Proceedings of the 13th IEEE International Conference on Computer Vision (ICCV),Barcelona, Spain, 2011 |
| [11] | Yu Wangsheng, Hou Zhiqiang, Song Jianjun. Color Image Segmentation Based on Marked-Watershed and Region-Merger [J]. Acta Electronic Sinica, 2011, 39(5): 1 007-1 012(余旺盛, 侯志强, 宋建军. 基于标记分水岭和区域合并的彩色图像分割[J]. 电子学报, 2011, 39(5): 1 007-1 012) |
| [12] | Comaniciu D, Meer P.Mean Shift: A Robust Approach Toward Feature Space Analysis [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603-619 |
 2015, Vol. 40
2015, Vol. 40


