文章信息
- 龙江平, 丁晓利
- LONG Jiangping, DING Xiaoli
- 利用矩阵值域的极化干涉SAR相干性的研究
- Polarimetric Interferometry SAR Coherence Using the Field of Matrix
- 武汉大学学报·信息科学版, 2015, 40(11): 1526-1532
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1526-1532
- http://dx.doi.org/10.13203/j.whugis20130321
-
文章历史
- 收稿日期: 2014-02-21

2. 香港理工大学土地测量与地理资讯学系, 香港, 999077
2. Department of Land Surveying and Geo-informatics, Hong Kong Polytechnic University, Hong Kong 999077, China
极化SAR干涉测量(PolInSAR)是结合极化技术和干涉技术,利用最优极化基对应的极化干涉相干性反演植被参数和散射介质等物理特征[1]。不同的极化状态会导致极化干涉的相干性不同[2, 3]。相干性的最优化问题可以转化为最优极化基的选择。极化干涉复相干的最优化是PolInSAR技术获取植被信息的基础,决定着植被参数信息提取的精度与可靠性[4]。PolInSAR植被参数反演是以相干性分析为基础,复相干矩阵是获取干涉相干性的前提。在极化空间中任意极化状态对应的极化干涉相干性理论上都应该分布在复相干矩阵确定的相干区域中[5]。在复平面中,各种散射机制对应的极化干涉相干性分布的区域称为相干集。
矩阵值域(the field of values)[6, 7]是刻划复矩阵在Hilbert[8]空间上的正交投影对与Hilbert空间上闭子空间对应关系。Hilbert子空间在PolInSAR技术中等价于相干集,Hilbert空间上的正交投影对等价于极化状态。Tabb和Flynn等人相继提出了复相干矩阵值域与干涉相干优化过程的关系[5, 9, 10, 11]。复相干矩阵估计偏差和散射机制对复相干矩阵值域的影响还需进一步研究。本文通过分析复矩阵值域几何性质和值域边界,研究复相干矩阵与最优极化相干的关系和影响因素,利用模拟和实际的全极化SAR数据分析了滑动窗口大小对复极化相干矩阵值域边界的影响,以及不同地物散射对复相干矩阵值域的分布形式,以便进一步地研究PolInSAR极化干涉相干优化处理过程。
1 极化干涉模型与矩阵值域 1.1 极化矢量干涉模型全极化SAR图像用极化散射矩阵 S 描述为:

在满足互易条件的散射场景下,全极化SAR散射矩阵可以表示为Pauli基矢量形式[1]:

在两次成像时可以获取对应的全极化数据,对每个像元形成两个矢量 K 1、 K 2,半正定的赫尔默特 T 6矩阵可以通过矢量的外积构成[12]:
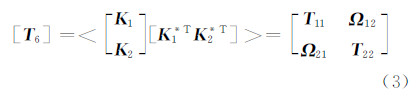
式中,[T 11]、[T 22]、[Ω 12]和[Ω 21]是3×3的复矩阵;*T表示共轭转置,其中:

式中,[T 11]和[T 22]是包含各自影像全极化信息的赫尔默特相干矩阵;[Ω 12]不仅含有极化信息,而且还含有两幅影像的干涉相位信息[13, 14]。
为了获得两个极化散射矢量表示的复干涉系数,定义单位复矢量 ω 1和 ω 2,记 μ 1和 μ 2为极化散射矢量 K 1、 K 2在 ω 1和 ω 2上的投影[15, 16, 17]:
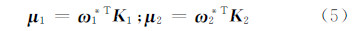
由式(5),半正定的赫尔默特 T 6矩阵可以改写成:
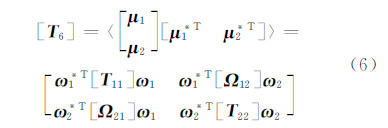
结合式(4)~式(6),复相干系数γ为[13, 14, 15, 16, 17, 18]:

在极化干涉相干优化过程中,为更好地理解相干矩阵,由 T 6定义简化相干矩阵为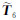 ,即有:
,即有:

式中,

Π 被称为简化相干矩阵。极化干涉复相干性可以由简化相干矩阵定义为:
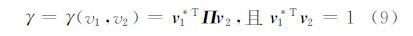
式中,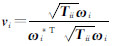
假设矩阵 A 为n×n的矩阵,矩阵 A 的值域可以定义为[19]:
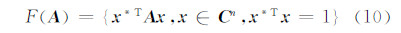
F( A )即为矩阵 A 的值域,它与矩阵的谱有很大的差别,矩阵的值域是一个连续凸集空间,表示该矩阵在Hilbert空间上的正交投影对与Hilbert空间上闭子空间对应关系,通过F( A )可以清楚了解矩阵的内部结构和性质[20, 21, 22, 23]。
根据式(9),可以得到基于简化相干矩阵对应的极化干涉矩阵的值域F( Π )[11],即
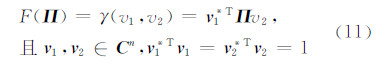
式(11)是在不同的散射机制下获取的复相干性,在一般的极化数据获取过程中,不考虑时间和空间的去相关影响,同一环境的散射机制一般认为是相同的,因此,单散射机制的极化干涉复相干系数可以表示为:

令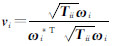 ,式(12)可以改写成:
,式(12)可以改写成:
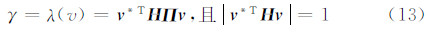
式(13)为散射机制相同的情况下对应的极化干涉复相干系数,该相干矩阵相应的值域为:
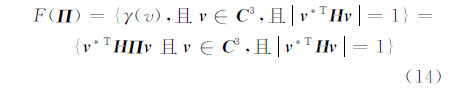
对于一个二维的矩阵,可以通过酉变换形成一个上三角矩阵 A [6],即
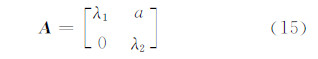
根据二维矩阵值域性质,矩阵 A 的值域边界是一个椭圆,相应椭圆的结构参数和形状可以从矩阵元素中获取,即矩阵的特征值λ1和λ2为椭圆的两个焦点,短轴为( 丨a丨 /2);当λ1=λ2时,矩阵 A 的值域退化为以原点为圆心,( 丨a丨 /2)为半径的圆;当a=0,且λ1≠λ2时,矩阵 A 的值域退化成以λ1和λ2为端点的直线;当a=0,且λ1=λ2时,矩阵 A 的值域退化成一个点。
2.2 复相干矩阵的值域复极化相干矩阵是3×3的复矩阵,根据矩阵Schur分解方法可以将复极化相干矩阵分解为一个上三角矩阵和一个酉矩阵 U 2[10, 15],即

根据式(15)中二维矩阵的数值域特点,极化相干矩阵对应的数值域是由3个二维子矩阵的数值域决定。复极化相干矩阵值域边界是与3个子矩阵各自数值域的外边界有关,并形成一个封闭紧凸集。
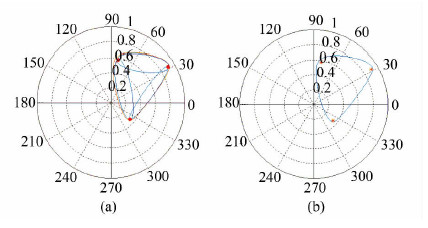
图 1(a)表示在复平面上极化干涉复相干矩阵对应的数值域,红色的点表示该相干矩阵对应的特征值,红色的线表示该矩阵值域对应的边界线,蓝色的线代表通过Schur变换后的上三角矩阵中各二阶子矩阵对应的值域。图 1(b)表示复平面上该复极化干涉矩阵对应的边界线。极化空间中可能的极化状态对应的干涉相干性分布在边界线构成的封闭区域内。最优极化干涉就是在相干矩阵值域构成的空间中寻找最优的散射机制,使得获取的干涉相干性最优。矩阵值域的值域半径对应的单位矢量就是使干涉相干幅度的达到最优对应的散射机制。
|
| 图 1 矩阵的值域 Fig. 1 The Field of Values of Matrix |
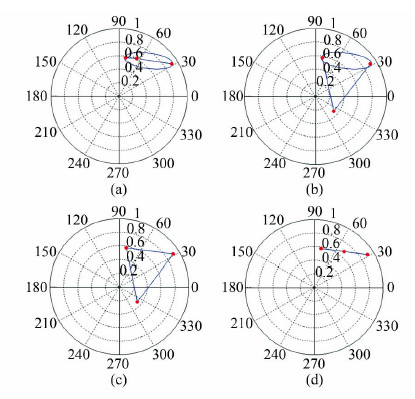
在式(16)中,利用Schur分解把复干涉矩阵分解为上三角矩阵,当上三角矩阵中非对角元素 b=0,c=0,则复相干矩阵的值域退化成一个由椭圆和一个特征值构成的几何结构,具体的几何结构与λ3有关。图 2(a)表示λ3在椭圆内或者椭圆上,相干矩阵值域表示为一个椭圆;图 2(b)表示为λ3在椭圆外时相干矩阵值域,该矩阵值域为凸集。当非主对角元素都为零时,复相干矩阵的值域为一个三角形,三角形的顶点是矩阵的特征值,其值域的几何结构如图 2(c)所示。当3个特征值存在线性组合,复矩阵的值域就退化成一条直线,如图 2(d)所示。
|
| 图 2 不同结构相干矩阵的值域 Fig. 2 The Field of Values of Coherence Matrix with Different Formation |
不同散射目标在理想情况下的散射机制分布在复相干矩阵值域空间内。对于理想情况下单纯地表散射或者体散射而言,其复相干矩阵对应的值域为一个点。在含有时间去相干时,复相干矩阵的值域是一段线段,其射向方向指向原点。
3 复极化相干矩阵的值域及相干性影响因素分析复极化相干矩阵值域包含的区域就是极化相干系数在极化空间中的取值范围,不同散射机制对应的相干性理论上都应该落在复相干矩阵值域对应的紧凸集中。在估计相干矩阵时,滑动窗口大小来决定估计样本数量以及样本的散射特性。窗口的选择既需要保证含有合理的样本数,也需要样本具有相同的散射特性。不同窗口大小和不同环境的散射目标,对复相干矩阵及其值域的估计都会产生影响。
3.1 滑动窗口对复相干矩阵值域的影响复极化相干矩阵的估计是在一定窗口下所有像元的赫尔默特乘积的数学期望,相干性的大小是衡量干涉质量优劣的主要指标。在极化SAR图像两次成像过程中,如果散射体对应的位置和散射机制不发生变化,雷达视线方向不改变,分辨单元内极化散射信号理论上保持不变。在自然环境中,复相干矩阵是采用滑动窗口估计来获取的。滑动窗口估计的相干矩阵和理论相干矩阵可能存在偏差。复相干矩阵估计的准确性与样本数目有很大关系,即滑动窗口越大,估计的复相干矩阵偏差越小,复相干矩阵值域的边界范围越准确,对应的极化干涉相干性分布越集中。
根据全极化SAR数据的特点,通过植被参数模拟植被覆盖的地形平坦区域极化SAR数据,具体的参数见表 1。以模拟极化SAR数据为基础,分别选取不同的滑动窗口来估计复相干矩阵,图 3(a)~图 3(d)分别是窗口大小为5×5、9×9、11×11和13×13时估计的复相干矩阵值域边界。不同颜色的点表示不同散射机制对应的极化干涉相干性在复极化干涉矩阵的值域边界中的分布。不同窗口大小决定了估计复相干矩阵的准确性。复相干矩阵值域边界的形状和范围与估计窗口有直接关系。图 3(a)中的复相干矩阵值域边界范围较大;图 3(d)中复相干矩阵的估计趋于稳定,其值域边界趋于准确,不同极化状态对应的相干性趋于集中。从图 3可以看出,滑动窗口的大小对复极化相干矩阵的值域边界有明显的影响,当窗口大到一定程度时,复相干矩阵的估计接近理论值,值域边界的变化也趋于稳定。

|
| 图 3 模拟SAR数据中窗口对相干矩阵值域的影响 Fig. 3 Influence of Window Sizes to the Field of Values of Coherence Matrix with Simulated SAR Data |
| 植被参数 | 数值 |
| 植被高度/m | 18 |
| 地表相位/(弧度) | 0 |
| 平均消光系数/(dB\5m-1) | 0.02 |
| 垂直波数 | 0.2 |
| 入射角/(°) | 30° |
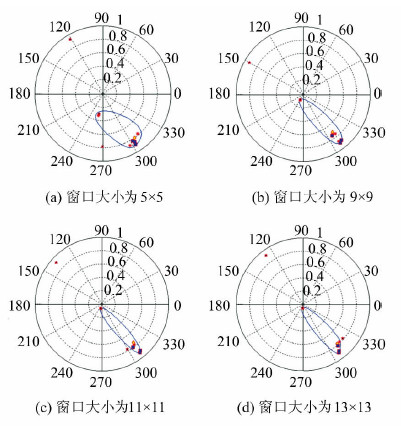
对比模拟数据,在真实的全极化SAR数据中,复极化相干矩阵的估计会受到各种噪声和失相干等因素的影响。滑动窗口对复相干矩阵的值域边界的影响比模拟数据更加复杂。图 4为1994年10月8日和9日美国航天飞机在贝加尔湖附近获取的L波段SIR-C数据中平坦的植被覆盖区域,选取的滑动窗口大小分别为5×5、9×9、11×11和13×13。不同滑动窗口估计的复相干矩阵的值域边界见图 4,离散点为不同极化状态对应的相干性。当滑动窗口变大时,复相干矩阵的值域边界范围随之变化,当滑动窗口大到一定程度时,复相干矩阵的值域边界趋于稳定。由于噪声和其他失相干等因素的影响,图 4中复相干矩阵的值域稳定后与理想情况有差异,部分极化状态对应的极化干涉相干性超出了值域边界的范围。
|
| 图 4 SIR-C 数据中窗口对相干矩阵值域的影响 Fig. 4 Influence of Window Sizes to the Field of Values of Coherence Matrix with SIR-C SAR Data |
从图 3和图 4中可以看出,不同散射机制的相干性落在值域空间中的位置有差异,代表该散射机制下相干性的强度和干涉相位的差异性,并且散射层的干涉中心相位以及反演的植被参数也存在差异。从图 3(d)和图 4(d)中可以看出,失相干和噪声等对复极化相干矩阵的值域边界的影响。图 3(d)中不同的最优原则下获取的最优极化相干性差异不大;而在图 4(d)中不同的最优原则获取的散射体相干性和相位有很大的差异。
通过增大滑动窗口估计复相干矩阵及其值域边界,使得极化相干性的分布范围趋于稳定,则极化相干性分布在在复平面内最小的区域,能在较小的范围内寻找最优的相干干涉,从而提高估计最优相干性的准确度。
3.2 散射目标对复相干矩阵值域的影响在SAR图像的分辨单元内,散射矩阵是该像元内一定空间分布的散射目标各自散射矩阵的相干叠加。散射矩阵与散射目标的形状、尺寸、空间位置和结构等物理参数相关,通过对以散射矩阵为基础的复极化相干矩阵的分析,可以反演相关物理参数。不同散射目标的散射矩阵差异性可以通过复相干矩阵的值域边界表达。
理论情况下,在没有时间去相干和信噪比去相干等影响时,无植被的地表散射复相干性仅仅与地形相位φ0相关,其极化干涉相干为:

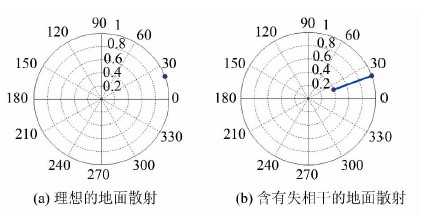
从式(17)可以看出,无植被地表散射的复相干矩阵值域在复平面内表示为一个点。当极化干涉存在时间去相干或者信噪比去相干时,复相干矩阵值域在复平面内表示为过原点的射线中某一段线段。图 5为理想的地面散射和含有去相干与信噪比影响的地面散射的复相干矩阵值域在复平面的表达。
|
| 图 5 地面散射相干矩阵的值域 Fig. 5 The Field of Values of Coherence Matrix with Surface Scatter |
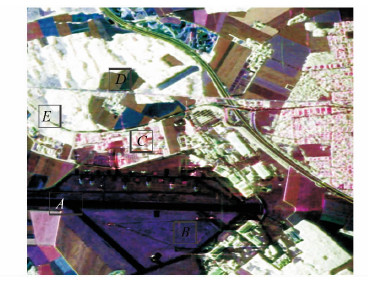
实际获取的SAR图像包含复杂地物环境,分辨单元内包含不同的散射相位中心,散射矩阵是各种散射特性的叠加。各种失相干因素会对散射矩阵产生影响,实际SAR图像中散射目标的复极化相干矩阵与理想情况有很大差异。本文选取机载E-SAR雷达传感器获取的德国Oberpfaffenhofen地区的全极化SAR实验数据。该实验区域散射类型丰富,包括植被覆盖区、机场跑道、草地、城市区和农田等不同的散射目标。图 6是该区域全极化SAR图像的Pauli基分解的合成图,不同地物如建筑物、植被和农作物可以清晰地分辨。从图 6中选择了A、B、C、D和E等5块地物目标不同的区域:A区域是机场跑道、B区域是草地、C区域是建筑区、D区域是农田区、E区域是植被区。
|
| 图 6 Oberpfaffenhofen区域的影像图 Fig. 6 Image of the Oberpfaffenhofen |
本文以图 6中的A、B、C、D和E等5个区域为基础,采用11×11滑动窗口估计复极化干涉矩阵,并计算复相干矩阵的值域边界。
图 7(a)是模拟地表散射数据的复相干矩阵的值域边界,没有失相干因素的影响,相干性与极化状态无关,地表散射的值域符合理论要求。图 7(b)~图 7(f)为5个不同散射类型的复相干矩阵值域边界,离散的点为不同极化状态下的相干性。图 6中A、B、C 3种散射类型的复相干矩阵值域范围图,离散的点为不同极化状态下的相干性。图 6中A、B、C 3种地物都属于地表散射为主的散射地物,A区域是机场跑道,在雷达后向散射过程中的相当于无植被覆盖地面散射,其干涉相干矩阵的值域见图 7(b),由于失相干因素影响,图 7(b)与理论情况下矩阵值域有一定的差异,但矩阵值域的主轴方向基本水平,仅仅含有地表散射相位中心。

|
| 图 7 不同散射类型的相干矩阵值域 Fig. 7 The Field of Values of Coheret Matrix with Different Scatters Type |
图 7(c)和图 7(d)分别代表草地和建筑区域的极化相干矩阵的值域,这两种地物的相干性比机场跑道的相干性高。由于草地的含水量比粗糙的机场跑道大,图 7(b)、图 7(c)复相干矩阵的值域形状和主轴方向基本一致,属于地面散射为主,但草地的极化相干性高。城市建筑区有很多金属和光滑材料,散射强度很强,相干性很高,相干矩阵的值域近似于一点,但由于失相干因素影响,和理论情况有差异。
图 6中D、E两种地物都属于体散射为主的散射地物,D区域是农田区,E区域是植被覆盖区域。两种散射体中既含有地表散射特性,也含有植被、农作物的散射信息,复极化相干矩阵的值域边界如图 7(e)、图 7(f)所示,极化干涉相干性的分布与极化状态有关,即极化相干矩阵的值域为一凸集,因此,最优极化相干性与极化干涉矩阵值域的主轴方向有关。复相干矩阵值域的边界表达了不同极化状态对应的相干性分布范围,以此来分离散射体相位中心。体散射目标的相干矩阵值域的大小和主轴方向与体散射的复介电常数、植被高度和消光系数等参数相关。从图 7(e)、图 7(f)可以看出,农田区的相干性比植被覆盖区高,由于农作物的方向性散射使得不同极化状态对应的相干性分布相对集中,而森林植被覆盖区最优极化选择取决于相干矩阵值域主轴方向。
在极化干涉相干性优化过程中,某一特定的最优准则下获取最优相干性应该分布在复相干矩阵的数值域空间中。不同散射地物的复相干矩阵的差异性也可以通过复相干矩阵值域来表达。散射地物对相干矩阵值域的影响主要体现在散射机制上,复相干矩阵值域为散射体相位中心分离提供了理论基础。
| [1] | Cloude S R, Papathanassiou K P. Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(51): 1 551-1 565 |
| [2] | Luo Huanmin,Chen Erxue,Cheng Jian, et al. Forest Height Estimation Methods Using Polarimetric SAR Interferometry[J]. Journal of Remote Sensing,2010,14(4):806-821(罗环敏,陈尔学,程建,等.极化干涉SAR森林高度反演方法研究[J].遥感学报,2010,14(4):806-821) |
| [3] | Tan Lulu,Chen Bing, Yang Ruliang. Improved Three-stage Algorithm of Tree Height Retrieval with PolInSAR Data[J]. Journal of System Simulation , 2010,22(4):996-999(谈璐璐,陈兵,杨汝良.利用PolInSAR数据反演植被高度的改进三阶段算法[J].系统仿真学报,2010,22(4):996-999) |
| [4] | Wu Yirong, Hong Wen, Wang Yanping. The Current Status and Implications of Polarimetric SAR Interferometry [J]. Journal of Electronics & Information Technology, 2007,29(5):1 258-1 262(吴一戎,洪文,王彦平.极化干涉SAR的研究现状与启示[J].电子与信息学报,2007,29(5):1 258-1 262) |
| [5] | Flynn T, Tabb M, Carande R. Coherence Region Shape Extraction for Vegetation Parameter Estimation in Polarimetric SAR Interferometry[C]. 2002 IEEE International Geoscience and Remote Sensing Symposium, Toronto,2002 |
| [6] | Horn R A, Johnson C R. Topics in Matrix Analysis [M].Cambridge:Cambridge University Press,1991 |
| [7] | Tabb M, Orrey J, Flynn T, et al.Phase Diversity: A Decomposition for Vegetation Parameter Estimation Using Polarimetric SAR Interferometry[C]. Proc EUSAR, Cologne, Germany,2002 |
| [8] | He C, Watson G A. An Algorithm for Computing the Numerical Radius[J]. IMA Journal of Numerical Analysis, 1997, 17(3): 329-342 |
| [9] | Tabb M, Iynn T, Carande R.Estimation and Removal of SNR and Scattering Degeneracy Effects from the Polinsar Coherence Region[C]. The 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003 |
| [10] | Neumann M, Reigber A, Ferro-Famil L, et al. PolInSAR Coherence Set Theory and Application[C]. EUSAR 2006, Dresden,2006 |
| [11] | Neumann M, Ferro-Famil L, Reigber A. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics From Multibaseline Polarimetric Interferometric SAR Data[J]. International Journal of Remote Sensing,2010, 48(3): 1 086-1 104 |
| [12] | Sagues L, Lopez-Sanchez J M, Fortuny J, et al. Indoor Experiments on Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 671-684 |
| [13] | Chen Bing, Zhang Ping. PolInSAR Data Simulation for Inversion Study Based on Scattering Model [J]. Journal of System Simulation, 2008,20(8):2 200-2 202(陈兵,张平.基于散射体模型的PolInSAR数据模拟反演研究[J].系统仿真学报, 2008,20(8):2 200-2 202) |
| [14] | Yang Zhen. Studies on Synthetic Aperture Radar Interferometric and Polarimetric Interferometric Techniques[D]. Beijing: Chinese Academy of Sciences,2003 (杨震.合成孔径雷达干涉与极化干涉技术研究[D].北京:中国科学院研究生院,2003) |
| [15] | Neumann M, Reigber A, Ferro-Famil L. Data Based on PolInSAR Coherence Shapes[C].2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea,2005 |
| [16] | Chen Erxue . Development of Forest Biomass Estimation Using SAR Data [J]. World Forestry Research , 1999, 12(6):18-23 (陈尔学.合成孔径雷达森林生物量估测研究进展[J].世界林业研究,1999,12(6):18-23) |
| [17] | Gong M. Coherence Optimization Using the Polarization State Conformation in Polinsar[J]. Geoscience and Remote Sensing Letters, 2005, 2(3): 301-305 |
| [18] | Bai Lu, Cao Fang, Hong Wen. Fast Approach to Estimate the Longest Axis in Coherence Region and Its Applications[J]. Journal of Electronics & Information Technology, 2010,32(3):548-553(白璐,曹芳,洪文.相干区域长轴的快速估计方法及其应用[J].电子与信息学报, 2010,32(3):548-553) |
| [19] | Chen Xi, Zhang Hong, Wang Chao. Vegetation Parameter Extraction Using Dual Baseline Polarimetric SAR Interferometry Data[J]. Journal of Electronics & Information Technology, 2008,30(12): 2 858-2 861(陈曦,张红,王超.双基线极化干涉合成孔径雷达的植被参数提取[J]. 电子与信息学报,2008,30(12):2 858-2 861) |
| [20] | Yang Jie, Shi Lei, Li Pingxiang. Wishart-H/Alpha Classification Based on Optimal Coherence and Polarimetric Span [J]. Geomatics and Information Science of Wuhan University, 2012,37(1):22-25(杨杰,史磊,李平湘.基于极化相干最优与极化总功率的Wishart-H/Alpha分类[J].武汉大学学报·信息科学版,2012,37(1):22-25) |
| [21] | Deng Shaoping, Li Pingxiang, Zhang Jixian, at al.Filtering of Polarimetric SAR Imagery Based on Multiplicative Model[J].Geomatics and Information Science of Wuhan University, 2011,36(10): 1 168-1 171 (邓少平, 李平湘, 张继贤, 等.基于乘积模型的极化 SAR 滤波[J]. 武汉大学学报·信息科学版,2011,36(10): 1 168-1 171) |
| [22] | He Chu, Liu Ming, Xu Lianyu. A Hierarchical Classification Method Based on Feature Selection and Adaptive Decision Tree for SAR Image[J]. Geomatics and Information Science of Wuhan University, 2012,37(1):46-49(何楚,刘明,许连玉.利用特征选择自适应决策树的层次SAR图像分类[J].武汉大学学报·信息科学版,2012,37(1):46-49) |
| [23] | Zhang Zhongshan,Yan Qin,Yu Jie, et al. Unsupervised Classification of Fully Polarimetric SAR Data Based on the PSO Algorithm[J].Geomatics and Information Science of Wuhan University,2010,35(8):941-945(张中山,燕琴,余洁,等. 基于粒子群算法的全极化SAR图像非监督分类算法研究[J]. 武汉大学学报·信息科学版, 2010,35(8):941-945) |
 2015, Vol. 40
2015, Vol. 40


