文章信息
- 刘文超, 卞鸿巍, 王荣颖, 温朝江
- LIU Wenchao, BIAN Hongwei, WANG Rongying, WEN Chaojiang
- 惯导系统横向坐标法导航性能研究
- Navigation Performance of SINS Transverse Coordinate Method
- 武汉大学学报·信息科学版, 2015, 40(11): 1520-1525
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1520-1525
- http://dx.doi.org/10.13203/j.whugis20130032
-
文章历史
- 收稿日期: 2014-09-04

极区导航环境非常复杂,影响多种现有导航设备的正常使用[1, 2, 3]。惯性导航系统[4]因其具有自主性、抗干扰性、隐蔽性等优势,使其成为军事上一种必要的导航手段,在环境复杂的极区导航中也显得尤为重要。但惯导系统传统地理经纬坐标解算方法在近极点区域存在解算奇异和系统误差过大的问题,通常采用横向坐标法解决。文献[5, 6, 7]均应用横向坐标系(网格坐标系/高斯直角坐标系/逆向坐标系)来解决惯导的解算奇异,但具体实行方法的相关文献鲜见发表;文献[8]采用横向坐标系(苏门答腊坐标系)进行惯导解算,但惯导的力学编排并不完整,也未对该方法在极区的应用进行性能评估;文献[9]应用横向坐标系解决惯导的解算奇异问题,并未对横向坐标法及其导航性能进行系统的研究。
本文在研究惯导横向坐标系下解算的基础上,对横向坐标法的导航性能进行了研究,通过推导惯导系统在横向坐标系下的系统误差方程和求解静基座状态下的系统误差方程,研究系统初始误差和惯性测量元件误差对基于横向坐标法的惯导系统的影响。
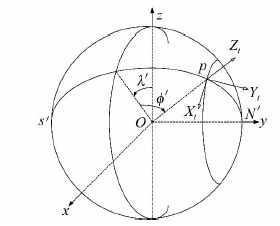
1 横向坐标法系统误差方程为解决近极点区域惯导系统解算奇异和系统误差过大的问题,采用横向坐标法,该方法是将极区的经纬度重新人为规定[9],使原坐标系的南北极移到横向赤道平面上的零经纬度,横向经度 (φ′)和横向纬度(λ′)的具体定义如图 1所示。横向坐标系(t系)的原点就是载体所在点,Zt轴沿参考球体的法线指向天顶,Xt轴与Yt轴均与Zt轴垂直,即在当地水平面内,Xt轴沿横向纬度线指向横向正东,Yt轴沿当地横向子午线指向横向正北。
|
| 图 1 横向坐标系示意图 Fig. 1 Digram of Transverse Coordinate System |
本文以捷联惯导系统为研究对象,取导航坐标系为t系,解算方程如下(推导从略)。
1) 速度更新方程
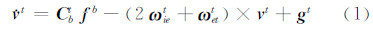
式中,v t=[vEt vNt vUt]T为横向速度; C tb为载体坐标系(b系)到横向坐标系(t系)的方向余弦阵; ƒ b=[ƒx ƒy ƒz]T为比力; ω tet=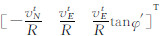 为t系相对地球坐标系(e系)的角速度;R为平均曲率半径; g t为重力; ω iet=[-ωiesinλ′ -ωiesinφ′cosλ′ ωiecosφ′cosλ′]T为地球自转角速度 ω ie在t系内的投影。
为t系相对地球坐标系(e系)的角速度;R为平均曲率半径; g t为重力; ω iet=[-ωiesinλ′ -ωiesinφ′cosλ′ ωiecosφ′cosλ′]T为地球自转角速度 ω ie在t系内的投影。
2) 姿态更新方程为:
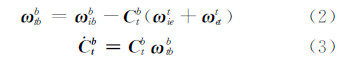
式中,ω btb为姿态角速率; ω bib为陀螺测量角速率。
3) 位置更新方程为:
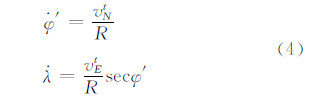
从以上解算方程可以看出,在近极点区域即(φ′,λ′)趋于(0,0)的区域内,该方法未出现计算奇异,而采用地理经纬坐标解算方法[9],当地理纬度φ趋于90°时,计算三角函数或者反三角函数会出现计算溢出,因此,横向坐标系法可以解决计算奇异问题。
同时,为分析其导航性能,需对惯导横向坐标法系统误差方程进行推导。
1.1 速度误差方程根据式(1),用计算值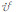 减去真实值
减去真实值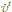 ,并忽略重力误差及高阶小量,得到横向速度系统误差为:
,并忽略重力误差及高阶小量,得到横向速度系统误差为:
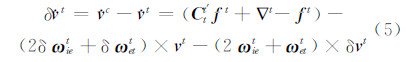
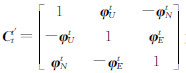 为理想导航系到导航系的姿态角方向余弦矩阵; φ Et、 φ tN、 φ tU为姿态误差;
为理想导航系到导航系的姿态角方向余弦矩阵; φ Et、 φ tN、 φ tU为姿态误差; 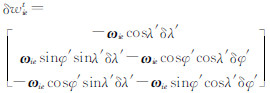 为导航坐标系中地球自转角速度误差;
为导航坐标系中地球自转角速度误差;
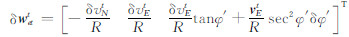
将上述关系式代入式(5),不考虑垂直通道,得:
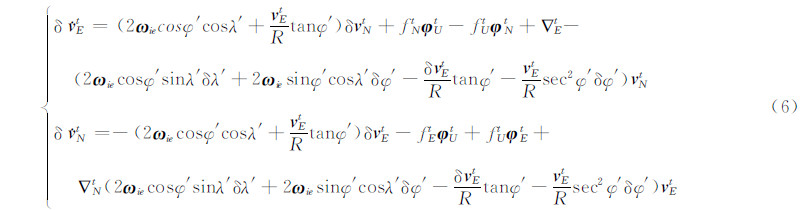
姿态误差是指导航坐标系相对理想导航坐标系之间的偏差角 φ t,满足
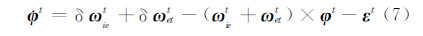
式中,ε t=[εEt εNt εUt]T= C bp[εx εy εz]T为导航坐标系下等效陀螺漂移,εx、εy、εz分别为b系下x、y、z方向上的陀螺噪声。
将各项代入式(7)可得:
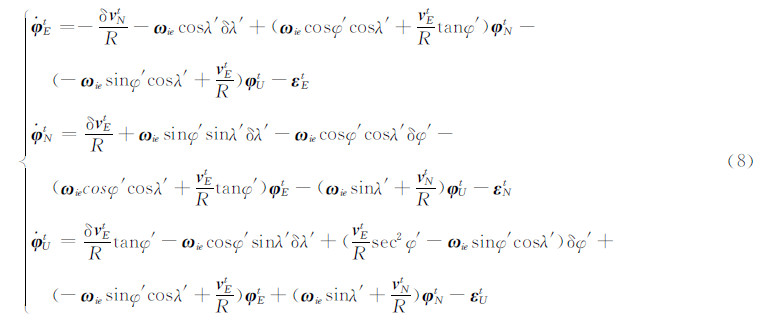
根据式(4),用计算值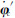 和
和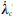 减去真实值
减去真实值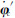 和
和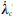 ,可得到横向经度和纬度误差分别为:
,可得到横向经度和纬度误差分别为:
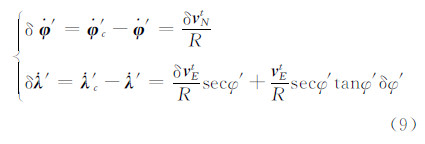
在惯导系统误差方程基础上,将静基座条件 v Et= v Nt=0,ƒEt =ƒNt =0,ƒUt =g分別代入式(6)、式(8)和式(9)可得惯导静基座下误差方程,然后对惯导系统系统误差基本传播特性进行分析。
2.1 误差状态方程特征根为了解系统误差的震荡特性和各误差源对惯导系统的影响,将静基座误差方程写成状态矩阵形式:
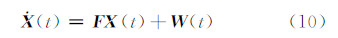
进行拉普拉斯变换得:
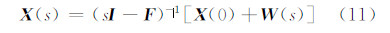
用Mathematica软件推导可得系统的特征方程:
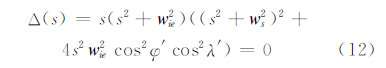
式中,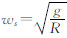 为舒拉角频率。
为舒拉角频率。
对各特征方程求解,并考虑 ws2»w ie2,可得近似特征根分别为:
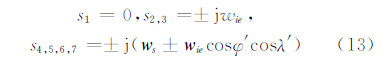
式中,w iecosφ′cosλ′= w iesinφ为傅科频率。
可以看出其特征值除一个零根外,其他均为虚根,说明7个误差量是周期性震荡的,该系统处于临界稳定状态。各系统误差包含地球自转周期、舒拉周期和傅科周期震荡成分。
2.2 系统误差传播特性分析为了简化计算,忽略了由于补偿有害加速度不完全引入的傅科周期,即F(1,2)=F(2,1)=0。
为较直观地得出每一种误差源引起的系统误差特性,设加速度零偏和陀螺漂移都是常值,推导可得各惯性测量元件误差引起的横向坐标系下的系统误差如下:

由式(14)~式(20)可以看出,等效东向加速度计误差产生δλ′、 ΦNt和ΦUt的常值误差;等效北向加速度计误差δφ′和φ Et的常值误差;等效东向陀螺漂移产生δv tE、δv Nt和δλ′的常值误差,产生δφ′、δλ′和Φ Ut的随时间增长的误差;等效北向陀螺漂移产生δv Et、δv tN、δφ′和ΦUt的常值误差,产生δφ′、δλ′和ΦUt的随时间增长的误差;方位陀螺漂移产生δv′E、δv′N、δφ′、δλ′和δKt的常值误差,产生δφ′、δλ′和ΦUt的随时间增长的误差。其余误差为震荡性误差。
与采用地理经纬坐标解算方法的系统误差分析结果[9]相比,存在两点明显的不同:δφ′中包含随时间增长的误差,而地理纬度误差δφ则不包含;地理经纬坐标解算方法的方位误差角ΦUg与secφ、tanφ相关,在极区该误差会明显增大,而ΦUt与secφ′、tanφ′相关,secφ′、tanφ′在极区较小,不会引起 ΦUt增大,因此,采用横向坐标系法可以解决系统误差过大的问题,但ΦUt包含随时间增长的误差,需要定时校正。
2.3 初始参数误差引起的系统误差由于初始姿态误差φ tE0、φ tN0、φ tU0的输入点与等效陀螺漂移ε tE、ε tN、ε tU的输入之间分别相差一个积分环节;初始速度误差δv tE0、δv tN0与等效加速度计误差∇tE、∇Nt的输入点之间分别相差一个积分环节。这表明初始误差对于系统的影响要少一个积分环节,因此,ΦE0t、 ΦN0t、ΦU0t产生δφ′、δλ′和ΦUt的常值误差,利用上述系统误差传播特性的分析方法分析初始位置误差对系统误差的影响,可得δφ′0产生δφ′、δλ′和ΦUt的常值误差。其余初始系统误差引起的系统误差均为震荡性误差。
3 仿真实验与结果分析为了验证误差分析结果推导的正确性,假设惯导工作在静基座条件,以隔离载体运动影响对捷联惯导系统误差特性的分析。设载体初始位置为(89.9°N,45°E);惯导系统的陀螺常值漂移为0.001°/h,随机漂移为0.001°/h;加速度计常值误差为10-5g,随机误差为10-5g。惯导导航信息的初始误差为:水平姿态误差为30°,方位角误差为30″,初始位置误差为10 m,初始速度误差均为0.01 m/s。仿真时间为24 h,仿真结果如图 2所示。
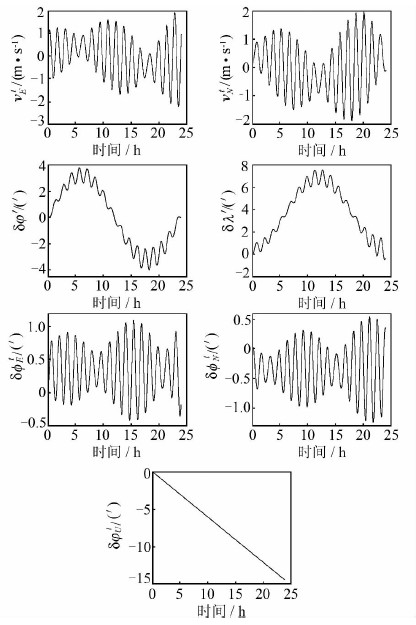
|
| 图 2 惯导系统横向坐标法系统误差 Fig. 2 System Errors of Transverse Coordinate Method |
从图 3可以看出,δv tN、δv tE为周期震荡性误差,ΦtE、ΦtN为常值误差与周期震荡性误差之和,ΦUt主要受随时间增长的误差影响,但δv tE、δv tN的常值误差和δφ′、δλ′的随时间增长的误差在上述仿真条件下的表现并不明显,这是因为在极区φ′和λ′较小。 为验证这些误差推导的正确性,改变仿真位置为(30°N,60°E),其他仿真条件不变,仿真结果如图 3所示。
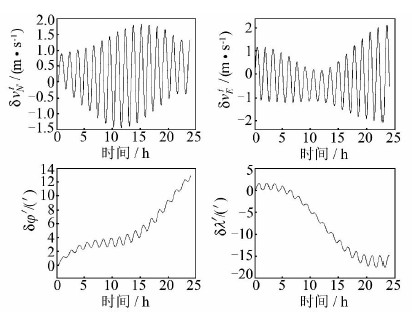
|
| 图 3 横向坐标法速度、位置误差 Fig. 3 Velocity and Position Errors of Transverse Coordinate Method |
从图 2可以看出,δv Et、δv Nt包含常值误差,δφ′、δλ′受随时间增长的误差的影响,因此,图 2和图 3验证了横向坐标系法误差分析结果的正确性。
比较横向坐标系法与采用地理经纬坐标解算方法,设置以下仿真条件:载体沿格林威治子午线由位置(85°N,0°)以10 m/s的速度航行穿过北极点,其他条件与以上仿真条件相同。仿真结果如图 4所示。
从图 4可以看出,采用地理经纬坐标解算方法系统误差在穿越极点前后会迅速的增大,这是因为方位角误差随纬度升高而增大,由于误差之间的耦合关系进而影响其他导航参数误差,直至某纬度使系统丧失导航能力。而横向坐标系法的系统误差在在穿越极点前后较小,因此,横向坐标系法可以有效解决惯导地理经纬坐标解算方法极区导航系统误差过大的问题,有效提高惯导系统的极区导航性能。
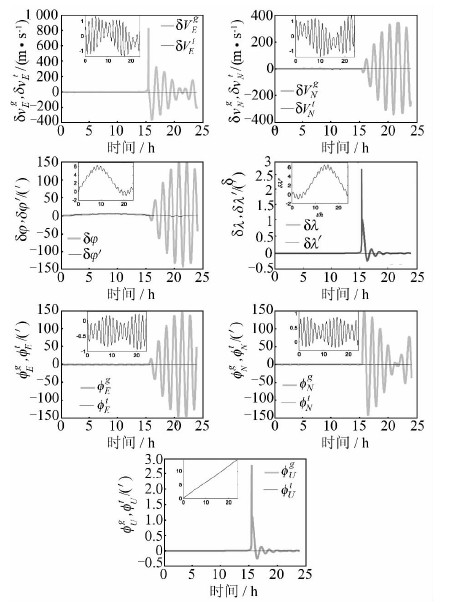
|
| 图 4 两种惯导解算方法误差比较 Fig. 4 Errors Comparision of Two SINS Computation Methods |
| [1] | Ye Ziyang.The Projections & Navigation Grid in Polar Navigation Chars[J].Navigation,1999(4):113-116(叶子扬.极区航空图投影及领航网格[J].导航,1999(4):113-116) |
| [2] | Barth D,Suzanna C.Evaluation of Tropospheric and Ionospheric Effects on Arctic Navigation Conditions[C].The 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation ION GNSS 2009,Savannah,2009 |
| [3] | McEwen R, Thomas H, Weber D, et al. Performance of an AUV Navigation System at Arctic Latitudes[J]. IEEE Journal of Oceanic Engineering, 2005, 30(2): 443-454 |
| [4] | Tazartes D A.From Gimbaled Platforms to Strapdwon Sensors[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(3):2 292-2 299 |
| [5] | Guo Deyin,Qu Shaobin,Jiang Lu, et al. A Practical Method of Locating at High Latitudes[J].Marine Technology,1999(4):16-19(郭德印,曲绍斌,姜璐,等.在高纬度地区确定船位的实用方法[J].航海技术,1999(4):16-19) |
| [6] | Paul G S.Strapdown Analysis[M].Minnesota:Strapdown Associats,2000 |
| [7] | Dyer G C.Polar Navigation——A New Transverse Mercator Technique[J].The Journal of Navigation,1971,24(4):484-495 |
| [8] | Watland D R. Orthogonal Polar Coordinate System to Accommodate Polar Navigation[P]. United States Patent,5448486, Minneapolis, MN, 1995 |
| [9] | Su Zhong, Li Qing, Li Kuangzhen, et al. Inertial Technique[M]. Beijing: National Defence Industrial Press, 2010(苏中,李擎,李旷振,等.惯性技术[M].北京:国防工业出版社,2010) |
 2015, Vol. 40
2015, Vol. 40


