文章信息
- 张烁, 徐亚明, 刘少创, 燕丹晨
- ZHANG Shuo, XU Yaming, LIU Shaochuang, YAN Danchen
- 嫦娥-3号月面巡视探测器立体相机的控制场检校
- Calibration of Chang'e-3 Lunar Rover Stereo-camera System Based on Control Field
- 武汉大学学报·信息科学版, 2015, 40(11): 1509-1513
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1509-1513
- http://dx.doi.org/10.13203/j.whugis20130610
-
文章历史
- 收稿日期: 2014-03-06

2. 中国科学院遥感与数字地球研究所空间信息综合集成技术研究室, 北京, 100101;
3. 国家海洋环境预报中心网络与计算机部, 北京, 100081
2. Department of Spatial Information Integrated Technology, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China;
3. Networks and Computer Department, National Marine Environmental Forecasting Center, Beijing 100081, China
月面巡视探测器是一种能够在月球表面执行巡视科学探测任务的航天器[1]。嫦娥-3号月面巡视探测器是我国自主研制的首个月面巡视探测器,它拥有我国最先进机器人的称号。嫦娥-3号月面巡视探测器安装了立体相机,利用立体相机除了能够对月表环境进行成像外,还能够用于巡视探测器的导航定位和着陆区域、巡视探测区域的地形恢复。为了满足月面巡视探测器导航定位和地形恢复的要求,需要对立体相机进行高精度的检校。
最早开展有关巡视探测器立体相机检校的是美国的JPL。Yakimovsky等提出了一种CAHV模型,该模型应用于美国的勇气号和机遇号火星巡视探测器的导航相机,用 C 、A 、H和V等4个矢量来表达从物方坐标到像方坐标的变换[2]。Gennery在CAHV模型的基础上,增加一个向量 O和一个三元组R 用以描述径向畸变,从而将CAHV模型改进为CAHVOR模型,CAHVOR模型正是勇气号和机遇号火星巡视探测器的全景相机采用的相机模型[3]。为了对勇气号和机遇号火星巡视探测器的避障相机(鱼眼镜头)进行建模,Gennery将CAHVOR模型改进为CAHVORE模型,增加的向量 E 用以重新描述光线束在像平面上投影的位置[4]。张正友提出利用对极几何关系实现巡视探测器立体相机的自检校,并建议在巡视探测器上安装检校物体[5]。王保丰等提出一种月面巡视探测器避障相机的两步法检校算法,该算法首先建立球面投影和透视投影之间的变换关系,然后将球面投影图像转换为透视投影图像,通过迭代计算获取相机参数的精确值[6]。
文献[2-4]提出的方法在美国MER计划中得到了很好的验证,文献[5-6]提出的方法也具有一定的适用性,但是上述模型与摄影测量的数学模型之间存在着复杂的转换关系,而嫦娥-3号月面巡视探测器的遥操作系统多采用摄影测量的数学模型,因此,上述方法不适用于我国的嫦娥-3号月面巡视探测器。
本文在深入分析和研究嫦娥-3号月面巡视探测器立体相机结构的基础上,推导了立体相机之间的固定相对关系表达式,采用了一种附有约束条件的间接平差模型,并通过真实数据验证了该方法的精度、稳定性和适用性。
1 立体相机及相对关系表达式 1.1 立体相机嫦娥-3号月面巡视探测器安装了一对导航相机、一对全景相机和一对避障相机。 其中避障相机固定安装在月面巡视探测器正前下方。而全景相机和导航相机则是安装在桅杆上方的云台上,可以根据探测任务的不同,在水平方向进行偏航和垂直方向俯仰。为了满足不同的任务目标,这3对相机的设计指标也有较大差异,如全景相机使用的是视场小的长焦距镜头;避障相机使用的是大视场的鱼眼镜头;而导航相机使用的则是中等视场、中等焦距的镜头。
图 1给出了立体相机的几何结构示意。其中,A-XYZ为物方坐标系,S1-X1Y1Z1为左相机坐标系,S2-X2Y2Z2为右相机坐标系,o1-x1y1为左像平面坐标系,o2-x2y2右像平面坐标系,S1为左相机摄影中心,S2为右相机摄影中心,o1为左像主点,o2为右像主点,f1为左相机主距,f2为右相机主距,P为空间任意一点,S1S2为立体相机基线距离。

|
| 图 1立体相机几何结构 Fig. 1 Geometric Structure of Stereo Camera |
右相机相对于左相机的空间关系可以用旋转矩阵 R e和平移量[Xe,Ye,Ze]T来描述,R e采用φe、ωe和κe的转角系统进行构造。左相机所拍摄像片的外方位角元素可以用旋转角φl、ωl和κl表示,其构成的旋转矩阵表示为 R l,外方位线元素用(XS l,YS l,ZS l)表示;同理,右相机所拍摄像片的外方位角元素用旋转角φr、ωr和κr表示,其构成的旋转矩阵表示为 R r,外方位线元素用(XS r,YS r,ZS r)表示。则左右像片外方位元素的关系表达式为[7]:
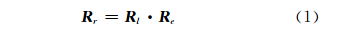
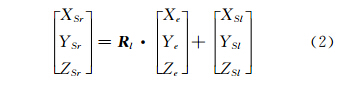
在透视投影的方式下,经过投影中心、像点和物方点的光线束可以用共线方程来描述,具体表达式如下式[7]:
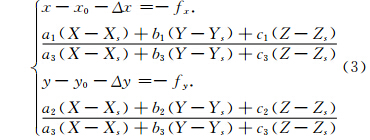
畸变模型取如下形式[7]:
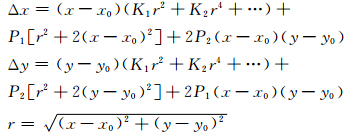
式中,K1、K2、…表示径向畸变系数;P1、P2表示切向畸变系数,研究表明,切向畸变所引起的误差大约为径向畸变的1/7~1/8[7]。对于导航相机和全景相机径向畸变系数取K1、K2。对于大畸变的避障相机,径向畸变系数取K1、K2、K3、K4、K5。
线性展开式(3),推导出误差方程式[7]:
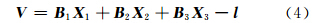
式中,V 为像点坐标的改正数向量; X 1为外方位元素的增量向量; B 1为对应的系数矩阵; X 2为物方点坐标的增量向量; B 2为对应的系数矩阵; X 3为内方位元素和畸变参数的增量向量; B 3为对应的系数矩阵;l 为像点坐标的残差向量。
2.2 相对关系约束条件假设利用立体相机拍摄了n对立体影像,对于第i对影像和第j对影像都存在式(1)和式(2)所描述的几何关系,利用旋转矩阵的正交性质,得到如下约束关系[8]:
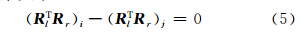
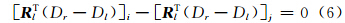
式中,i和j分别表示第i和第j像对;Dl和Dr分别表示左右像片的外方位线元素。由旋转矩阵的正交性可知,式(5)中的9个元素只有3个是相互独立的,旋转矩阵可以通过选用的3个独立元素进行表示。本文选取式(5)所描述的3×3正交矩阵的对角线元素上方的3个元素为独立元素,结合式(6)共同作为限制条件,其表达式如下[8]:

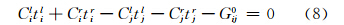
式中,til、tir、tjl和tjr为外方位元素的改正数;Cil、Cir、Cjl和Cjr为Gij对外方位元素的偏导数;G0ij为将各个相关的外方位元素初值带入Gij所得到的常数。
2.3 立体相机的检校模型将式(8)作为式(4)的强制约束条件,则检校模型优化为式(9)所示形式:
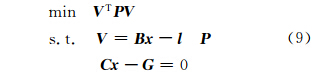
式中,V 为像点坐标的改正数向量; x 为检校参数的增量向量,B 为对应系数矩阵; l 为像点坐标的残差向量; C和G 分别为约束方程的系数矩阵和常数项; P 为权矩阵。该模型为附有约束条件的间接平差模型,采用最小二乘法求解该模型。
3 试验及结果分析 3.1 试验概述利用2013年8~9月,嫦娥-3号月面巡视探测器相机检校试验的数据,以导航相机为例,采用本文算法(附有约束条件的间接平差算法(简称方法1)和自检校光束法平差(简称方法2))进行处 理。本次试验在一洁净度极高的室内环境下开 展。在相机视场范围内均匀布设了101个标志点,其中有71个为控制点,有30个为检查点,控制点的坐标采用全站仪和标准尺,通过前方交会的方法获取,全站仪型号为徕卡TS06,测角精度为2″。测量控制点的残差中误差和测量检查点的误差中误差如表 1所示。
| 项目 | 控制点 | 检查点 |
| 平面误差的中误差 | 0.227 28 | 0.235 30 |
| 高程误差的中误差 | 0.275 28 | 0.251 95 |
月面巡视探测器固定安装在支架车上,导航相机距离地面高度约2 m。桅杆的展开角、偏航角和俯仰角固定为0°、0°和-35°,通过移动月面巡视探测器分别从8个不同的位置对控制场成像,获取8对立体像对。成像的瞬间,安装在月面巡视探测器上的IMU和里程计会获取车体在物方坐标系下的位置和姿态,经过一系列的坐标转换将车体的位置和姿态转换为像片的外方位元素初始值,坐标转换的过程中,需借助IGPS测定坐标系之间固定的旋转矩阵和偏移量。在提取像点坐标时,采用人工提点的方式,首先对待提点的局部区域进行梯度倒数加权平滑,然后将此区域放大10倍,最后提取出该像点的坐标值,提取精度达到亚像素级。
3.2 检校结果的中误差表 2给出了利用方法1和方法2对左导航相机和右导航相机的内参数进行检校得到的中误差结果。
| 参数项 | 方法1 | 方法2 | ||
| 左相机 | 右相机 | 左相机 | 右相机 | |
| σ 0 | 0.075 83 | 0.081 40 | 0.096 32 | 0.105 87 |
| σ x 0 | 0.144 98 | 0.137 09 | 0.253 61 | 0.606 51 |
| σ y 0 | 0.291 14 | 0.292 08 | 0.430 90 | 0.537 02 |
| σ f x | 0.156 04 | 0.177 54 | 0.366 14 | 0.263 16 |
| σ f y | 0.139 52 | 0.158 74 | 0.362 31 | 0.248 63 |
| σ K1 | 1.163 82×10 -9 | 1.758 67×10 -9 | 3.958 45×10 -9 | 4.350 37×10 -9 |
| σ K2 | 3.390 98×10 -15 | 4.890 35×10 -15 | 1.119 39×10 -14 | 1.254 79×10 -14 |
| σ P1 | 1.502 91×10 -7 | 2.545 89×10 -7 | 3.418 72×10 -7 | 3.251 08×10 -7 |
| σ P2 | 1.160 73×10 -7 | 1.862 14×10 -7 | 4.655 86×10 -7 | 4.048 37×10 -7 |
从表 2的统计结果中可以看出,方法1计算得到的单位权中误差和内参数中误差要优于方法2的结果,这在对左导航相机和右导航相机的检校过程中呈现出一致的规律性。因此,方法1要比方法2具有更高的精度。
表 3给出了利用方法1和方法2计算得到的导航相机相对关系参数的中误差统计结果。
| 参数项 | 方法1 | 方法2 |
| σ X e /mm | 0.127 26 | 0.336 49 |
| σ Y e /mm | 0.149 05 | 0.200 71 |
| σ Z e /mm | 0.641 63 | 0.965 27 |
| σ φ e /(°) | 0.010 37 | 0.023 21 |
| σ ω e /(°) | 0.046 26 | 0.062 00 |
| σ κ e /(°) | 0.006 31 | 0.006 87 |
从表 3的统计结果中可以看出,利用方法1计算得到的导航相机相对关系参数的中误差要优 于方法2的结果。不论是方法1还是方法2,线 元素的Ze分量的中误差要大于Xe和Ye分量的中误差,这说明控制点在Z方向上的控制强度要弱于X和Y方向。由于方法1将左右导航相机的相对关系作为强制约束条件与误差方程一起进 行平差处理,所以导航相机的相对关系参数是检校模型的直接求解参数,最终从不同的立体像对计算的相对关系参数都相等。而对于方法2,虽然理论上由不同立体像对计算出来的相对关系参数是一致的,但是由于误差的存在,实际得到的参数存在差别。因此,方法1要比方法2具有更高的精度和稳定性。
3.3 检查点误差利用方法1和方法2计算所得的导航相机内参数和外方位元素,采用多片前方交会计算检查点在物方坐标系下的坐标,并与全站仪测得的检查点坐标进行对比,统计结果如表 4所示。
| 方法 | 最大残差 | 最小残差 | 中误差 | ||||||
| X | Y | Z | X | Y | Z | X | Y | Z | |
| 方法1 | -0.094 | 0.075 | -0.102 | 0.022 | 0.034 | -0.060 | 0.067 | 0.049 | 0.081 |
| 方法2 | 0.136 | 0.096 | -0.163 | -0.045 | 0.062 | -0.083 | 0.090 | 0.076 | 0.115 |
从表 4的统计结果中可以看出,利用方法1计算得到的检查点的误差小于方法2。因此,利用方法1得到的检校结果对目标点进行定位比利用方法2具有更高的精度。不论是方法1还是方法2,检查点在Z方向上的误差要大于X和Y方向,这进一步证明控制点在Z方向上的控制强度要弱于X和Y方向。
4 结 语本文采用一种附有约束条件的间接平差模型对嫦娥-3号月面巡视探测器的导航相机、全景相机和避障相机进行检校。以导航相机拍摄的数据为例进行试验,试验结果证明:①立体相机之间固定相对关系约束条件的引入,能够使自检校光束法平差具有更强的稳健性,并在一定程度上提高了检校的精度;②该方法能够用于对嫦娥-3号月面巡视探测器的立体相机进行高精度的检校。
| [1] | Alexander D A, Deen R G, Andres P M, et al. Processing of Mars Exploration Rover Imagery for Science and Operations Planning [J]. Journal of Geophysical Research, 2006, 111(2):1-21 |
| [2] | Yakimovsky Y, Cunningham R. A System for Extracting Three-Dimensional Measurements from a Stereo Pair of TV Cameras [J]. Computer Graphics and Image Processing, 1978, 7(2):195-210 |
| [3] | Gennery D B. Least-Squares Camera Calibration Including Lens Distortion and Automatic Editing of Calibration Points [J]. Calibration and Orientation of Cameras in Computer Vision, 2001, 34(1):123-136 |
| [4] | Gennery D B. Generalized Camera Calibration Including Fish-Eye Lenses [J]. International Journal of Computer Vision, 2006, 68(3):239-266 |
| [5] | Zhang Zhengyou. A Stereovision System for a Planetary Rover: Calibration, Correlation, Registration and Fusion [J]. Machine Vision and Applications, 1997, 10(1):27-34 |
| [6] | Wang Baofeng, Mao Xiaoyan, Tang Geshi. A Calibration Method for Fish-Eye Camera of Lunar Rover [J]. Journal of Astronautics, 2011, 32(4):933-939(王保丰, 毛晓艳, 唐歌实. 月球车鱼眼相机的检校方法研究 [J]. 宇航学报, 2011, 32(4):933-939) |
| [7] | Wang Zhizhuo. Photogrammetry [M]. Wuhan: Wuhan University Press, 2007(王之卓. 摄影测量原理 [M]. 武汉: 武汉大学出版社, 2007) |
| [8] | Zheng Shunyi, Huang Rongyong, Guo Baoyun, et al. Stereo-camera Calibration with Restrictive Constraints [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6):877-885(郑顺义, 黄荣永, 郭宝云, 等. 附约束条件的立体相机标定方法 [J]. 测绘学报, 2012, 41(6):877-885) |
| [9] | Ke Tao, Zhang Zuxun, Zhang Jianqing. Panning and Multi-baseline Digital Close-range Photogrammetry [J]. Geomatics and Information Science of Wuhan University, 34(1):44-47(柯涛, 张祖勋, 张剑清. 旋转多基线数字近景摄影测量 [J]. 武汉大学学报·信息科学版, 2009, 34(1): 44-47) |
| [10] | Tan Xiaojun, Yu Zhi, Li Jun. An Improved Method of Stereo Camera Calibration [J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 138-142(谭晓军, 余志, 李军. 一种改进的立体摄像机标定方法 [J]. 测绘学报, 2006, 35(2): 138-142) |
| [11] | Blonquist K F, Pack R T. A Bundle Adjustment Approach with Inner Constraints for the Scaled Orthographic Projection [J]. Journal of Photogrammetry and Remote Sensing, 2011, 66(7): 919-926 |
| [12] | Espuny F, Burgos Gil J I. Generic Self-Calibration of Central Cameras from Two Rotational Flows [J]. International Journal of Computer Vision, 2011, 91(2): 131-145 |
 2015, Vol. 40
2015, Vol. 40



