文章信息
- 温朝江, 卞鸿巍, 边少锋, 魏学通
- WEN Chaojiang, BIAN Hongwei, BIAN Shaofeng, WEI Xuetong
- 基于等距圆的极球面投影距离量测方法
- A Distance Measuring Method on Polar Stereographic Charts Based on Equidistant Circles
- 武汉大学学报·信息科学版, 2015, 40(11): 1504-1508,1513
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1504-1508,1513
- http://dx.doi.org/10.13203/j.whugis20130759
-
文章历史
- 收稿日期: 2013-12-09

2. 海军工程大学导航工程系, 湖北 武汉, 430033
2. Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033, China
随着北冰洋冰盖消融,北极航运的战略价值凸显[1],海图是安全利用北极航线的基础,墨卡托投影海图由于长度变形过大而不宜使用[2]。极球面投影(等角方位投影)在极区具有等角、变形小、大圆航线接近直线等优点,极有可能作为极区海图首选投影方式[3, 4, 5, 6, 7, 8, 9]。距离量测是基本的图上作业样式,主要基于直线实施,海图上通常量测的是等角航线距离(墨卡托海图)或大圆航线距离(日晷海图)[10, 11, 12]。极球面投影海图上除经线外的其他直线既非等角航线又非大圆航线,因此,需要探讨基于直线量测等角航距或大圆航距的可行性;同时,极球面投影图上,经线呈放射状分布导致沿经线分布的海里尺并不与矩形图框契合,因此,不能直接套用墨卡托海图或日晷海图上的量距方法[11]。
复杂恶劣的航行环境长期严重限制了极区通航需求,导致人们对极区航海图不够关注,极球面投影的极区应用研究并不系统和充分,现有经典地图投影教材的相关章节停留在对投影坐标及变形特点的简略陈述,其他文献集中在其极区可用性分析及格网导航应用方法等方面[5, 6, 7, 8, 12, 13],缺乏对该投影下精确量距方法的研究,这已成为该投影应用亟待解决的重要问题。本文推导了极球面投影上大圆航线与等角航线方程,分析了直线代替大圆航线量距的可行性;然后根据小圆线投影性质,提出了一种基于等距圆的极球面投影精确量距方法,以满足极球面投影海图上准确快速地量测距离的需要。
1 极球面投影上大圆航线的形状 1.1 极球面投影上大圆航线的方程与形状为便于推算,本文采用球面坐标(Z,α),其与地理坐标系(φ,λ)的关系为[10]:
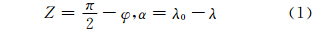
切于极点的正轴极球面投影坐标公式为[10]:
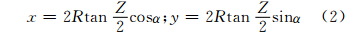
如图 1,球面上过A(Z,α1)、B(Z-ΔZ,α1+Δα),方向角为α′ 0的大圆航线方程[10]为:


|
| 图 2 球面上大圆航线示意图 Fig. 2Sketch of Great-circle Line on Earth |
当A、B两点同处于一经线圈时,大圆航线即为经线,形状为直线,其方程为:

当A、B两点不处于同一经线圈时,大圆航线方程为:

其中,

如图 2所示,A、B两点不处同一经线圈时,极球面投影上大圆航线是很接近直线的圆弧。

|
| 图 2 极球面投影上大圆航线与等角航线的形状 Fig. 2 Thumb Line and Great-circle Arc on Polar Stereographic Charts |
由文献[10]可知,(φ,λ)为航线上的动点,通过(φ1,λ1)、方位角为α的等角航线方程为:
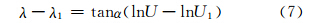
其中,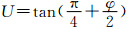 由式(2)、式(7)可得极球面投影上的等角航线方程:
由式(2)、式(7)可得极球面投影上的等角航线方程:
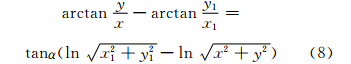
图 2中有一段航向为60°的等角航线,可见极球面投影上不沿经纬线的等角航线为螺旋形曲线。极区等角航程远大于大圆航程,大圆航线更接近直线,距离量测宜采用大圆距离。
2 直线与大圆航线的距离差值极球面投影上大圆航线是圆弧而非直线,因此,需要探讨极球面投影上直线的几何意义,以明确直线与大圆航线的关系并分析用直线近似量算大圆距离的可行性。
2.1 极球面投影上直线段的几何意义如图 3、图 4及图 5所示,投影平面为 P,地球面E的球心为O、半径为R、南北极点分别为S和N,E上任意两点A(Z,α)和B(Z-ΔZ,α+Δα)投影成A1(Z′ 1,α)、B1(Z′ 2,α+Δα′)。A、B间大圆线为 ,在平面P上投影成圆心Q、半径r的圆弧
,在平面P上投影成圆心Q、半径r的圆弧  。
。

|
| 图 3 极球面投影透视图 Fig. 3 Perspective Drawing of Polar Stereographic |

|
| 图 4 球面E上小圆线与球面E′上大圆线关系 Fig. 4 Sketch of Relationship Between Small-Circle on E and Great-Circle on E′ |

|
| 图 5 极球面投影上直线与大圆航线的关系 Fig. 5 Sketch of Relationship Between Straight Line and Great-Circle Arc on Polar Stereographic Charts |
在图 3中引入以S为球心、2R为半径的辅助球面E′,SA、SB与球面E′分别交于A′、B′两点。可见直线  不由等角航线和大圆航线投影而成,可看做S、A、B三点构成的平面与球面E的相交线
不由等角航线和大圆航线投影而成,可看做S、A、B三点构成的平面与球面E的相交线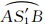 投影而来,由于平面截球体的轮廓是圆,其半径为r0,故
投影而来,由于平面截球体的轮廓是圆,其半径为r0,故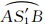 是△ASB的AB边所对的外接圆弧。
是△ASB的AB边所对的外接圆弧。
E上小圆线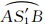 与E′上大圆线
与E′上大圆线 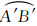 共面,对角同为∠ASB=θ,则
共面,对角同为∠ASB=θ,则 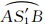 长度S1为:
长度S1为:
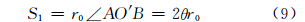
由图 4,E′上球面坐标(Z′,α′)满足

△ASB的外接圆半径r0满足:
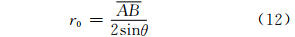
由图 5,△ASB中 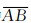 、
、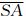 、
、 关系为:
关系为:


将式(10)~式(14)代入式(9)并整理,可得极球面投影上线段  对应的实地距离S1:
对应的实地距离S1:
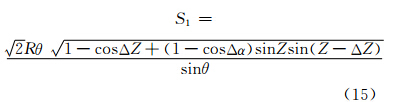
A、B间大圆线  的长度S2为[10]:
的长度S2为[10]:

设 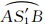 的长度S1与大圆线
的长度S1与大圆线  的长度S2的差值为ΔS,将ΔS用弧度(可转化为海里)表示:
的长度S2的差值为ΔS,将ΔS用弧度(可转化为海里)表示:

设ΔS与大圆航线长度S2的比例δ为:

图 6(b)和图 7(b)分别是Z=15°时ΔS和δ随ΔZ、Δα的变化趋势,右图分别是当ΔZ=0°、Δα=90°时ΔS和δ随Z的变化趋势。

|
| 图 6 ΔS随ΔZ、Δα和Z的变化趋势图 Fig. 6 Trends of ΔS Varing with ΔZ、Δα and Z |

|
| 图 7随ΔZ、Δα和Z的变化趋势 Fig. 7 Trends of δ Varing with ΔZ、Δα and Z |
1) ΔS和δ均随极距Z增大(纬度降低)而增大;随ΔZ(纬差)增大而减小;关于Δα=180°对称并呈正弦趋势变化,Δα=90°或270°时最大。
2) 在Z=0°~15°的高纬极区,Z=15°、ΔZ=0°、Δα=90°或270°时,航程误差ΔS最大达到0.062 8海里,误差比例δ最大达到0.005 %,均相当微小而可忽略。这是整个极区内的最大水平,而单幅大中比例尺海图覆盖的地理范围很有限,图上的量距误差会更加微小,这表明极区极球面投影上直线与大圆线航程非常接近,用直线代替大圆航线精确量距完全可行。
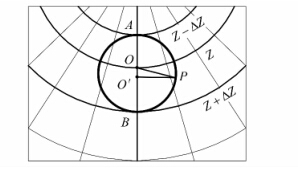
3 基于等距圆的精确量距方法 3.1 距离量测依据与作图方法如图 7所示,为便于计算不妨设图上线段 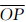 一端在α=270°的经线上。根据文献[10],与球面上某点O(Z,3π/2)距离为ΔZ的点P(Z′,3π/2+Δα)所构成的小圆,经过极球面投影后仍然为圆,设该圆M与过线段一端的经线交于A(Z-ΔZ,3π/2)、B(Z+ΔZ,3π/2)两点,则其圆心O′为线段
一端在α=270°的经线上。根据文献[10],与球面上某点O(Z,3π/2)距离为ΔZ的点P(Z′,3π/2+Δα)所构成的小圆,经过极球面投影后仍然为圆,设该圆M与过线段一端的经线交于A(Z-ΔZ,3π/2)、B(Z+ΔZ,3π/2)两点,则其圆心O′为线段  的中点。由于投影变形是极距Z的函数,圆心O′与O并不重合,而在O点更大极距一侧。根据该性质,通过绘制过线段任一端的等距圆,将图上任意直线段转化到过其一端,有精确纬度标记的经线上准确便捷地量距。
的中点。由于投影变形是极距Z的函数,圆心O′与O并不重合,而在O点更大极距一侧。根据该性质,通过绘制过线段任一端的等距圆,将图上任意直线段转化到过其一端,有精确纬度标记的经线上准确便捷地量距。
等距圆的尺规作图方法为:以经线为海里尺,在经线上选择O两侧纬差相等的两点A、B,以线段  为直径作圆直至过点P,即做出线段
为直径作圆直至过点P,即做出线段 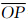 的等距圆。通过读取
的等距圆。通过读取  或
或 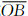 对应的纬度读数的差值便可准确量出
对应的纬度读数的差值便可准确量出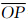 距离。如图 9所示,当线段过长而不便于作图时可适当分段作等距圆,然后将距离相加即可。
距离。如图 9所示,当线段过长而不便于作图时可适当分段作等距圆,然后将距离相加即可。
|
| 图 8等距圆示意图 Fig. 8 Sketch of Equidistant Circle |

|
| 图 9 线段分段量测示意图 Fig. 9Sketch of Distance Measuring by Segments |
等距圆可能需多次试作,长线段需做多个等距圆,操作仍有不便。因此考虑可否在合理误差范围内,在过线段 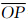 一端的经线上直接量取与
一端的经线上直接量取与 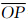 等长的线段
等长的线段  或
或 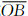 ,更简便地量测距离。
,更简便地量测距离。
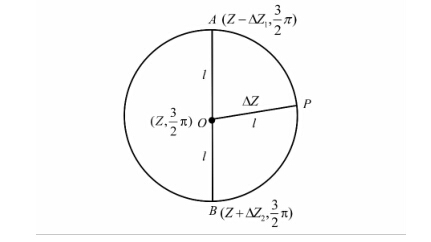
如图 10所示,极球面投影图上,以O点为圆心、 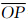 为半径的圆与过O点的经线交于A、B两点。
为半径的圆与过O点的经线交于A、B两点。 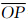 =l,各点坐标O(Z,3π/2),A(Z-ΔZ1,3π/2),B(Z+ΔZ2,3π/2),P(Z′,3π/2+Δα)。
=l,各点坐标O(Z,3π/2),A(Z-ΔZ1,3π/2),B(Z+ΔZ2,3π/2),P(Z′,3π/2+Δα)。
|
| 图 10 直接距离量测示意图 Fig. 10 Sketch of Direct Distance Measuring |
受长度变形影响,  、
、 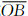 分别对应该圆上最大距离ΔZ1、最小距离ΔZ2,
分别对应该圆上最大距离ΔZ1、最小距离ΔZ2,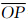 的实地距离ΔZ介于ΔZ1、ΔZ2间。其中:
的实地距离ΔZ介于ΔZ1、ΔZ2间。其中:
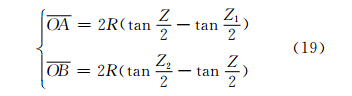
在比例尺为1/C的海图上,有:

令Ω=ΔZ1-ΔZ2,则ΔZ与ΔZ1、ΔZ2之差应不大于Ω。为Ω设定阈值ω,只要 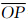 的图上长度l能使得Ω≤ω,就认为可通过
的图上长度l能使得Ω≤ω,就认为可通过  或
或 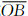 直接读出
直接读出 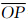 的距离ΔZ。由式(19)、式(20)可知,l须满足:
的距离ΔZ。由式(19)、式(20)可知,l须满足:

式(24)取等号时可得lmax,本文通过lmax考察l的取值范围。实际上,还可根据式(21)估计出直接量测距离l所对应的最大误差水平ω。阈值ω可以有多种形式,如图上长度δl、实地距离δz,或者差值Ω占最短距离ΔZ2的比例β等。
由式(21)可见,lmax与比例尺分母C成反比,随极距Z减小(纬度增大)而增大,随最小阈值ω增大而增大。线段较长时可如图 9所示分成小于lmax的数段分别量测后相加。
3.3 算例分析如表 1所示,考虑到航行一般采用大中比例尺航行图(1∶100万以下),本文将比例尺设为1∶50万,等角球半径R= 6 357 620 m(取与地球椭球体交于80°N的等角球体半径[10]),在1∶50万极球面投影海图上,ω取δl=0.1 mm、δz=0.1′、β=1‰,最低纬度75°N处lmax最小分别达到10 mm、19.23 mm和9.82 mm,在89°高纬度处甚至分别可达到38 cm、73 cm、146 cm,对于现有全张横幅(98 cm×66 cm)和全张直幅(68 cm×96 cm)海图[14],这些数值足以满足需要。
| φ/(°) | δ l=0.1mm | δ z=0.1′ | β=1‰ |
| 75 | 10.00 | 19.23 | 9.82 |
| 76 | 10.33 | 19.87 | 10.51 |
| 77 | 10.70 | 20.58 | 11.30 |
| 78 | 11.12 | 21.39 | 12.23 |
| 79 | 11.60 | 22.31 | 13.32 |
| 80 | 12.15 | 23.37 | 14.64 |
| 81 | 12.79 | 24.60 | 16.25 |
| 82 | 13.55 | 26.06 | 18.26 |
| 83 | 14.47 | 27.84 | 20.86 |
| 84 | 15.62 | 30.04 | 24.32 |
| 85 | 17.10 | 32.89 | 29.17 |
| 86 | 19.12 | 36.75 | 36.44 |
| 87 | 22.05 | 42.41 | 48.58 |
| 88 | 27.00 | 51.93 | 72.87 |
| 89 | 38.18 | 73.45 | 145.96 |
| 90 | ∞ | ∞ | ∞ |
海图作业时,通过设定合理的阈值 ω,将图幅南图廓处lmax设为全图的lmax,过长的线段可分段量测。更大比例尺、更宽松阈值ω和更高纬度处,lmax还将大幅乃至成倍增大,将进一步改善直接量距法的可用性,以满足极区用图需要。更小比例尺海图上,可通过适当放宽阈值ω增大lmax以便于量测,或者通过绘制等距圆来量测距离。
4 结 语本文根据极区航海图使用需要,论证了极球面投影海图上基于直线量测大圆距离的可行性,并利用小圆线的极球面投影性质,提出了基于等距圆的极球面投影海图精确便捷的量距方法。研究表明:极球面投影上大圆航线投影成圆弧,等角航线投影投影成螺旋线,大圆距离远小于等角距离,距离量测宜采用大圆距离;极球面投影海图上直线是由过南极点与航线始末点的小圆线而来,极区范围内该圆弧与大圆航线的距离差值极小,用直线代替大圆弧线较精确地量距是可行的;小圆线经极球面投影后仍为圆,据此可在极球面投影海图上作等距圆,将任意线段转换到作为海里尺的经线上精确量距;在合理误差范围内,一定长度的图上线段可通过在过线段一端的经线上量取等长线段来直接量距,给出了该长度的估算公式,过长的线段可分段量测然后相加即可。
| [1] | Global Business Network(GBN).The Future of Arctic Marine Navigation in Mid-Century[R]. Scenario Narratices Produced for the Protection of the Arctic Marine Environment (PAME) Woking Group, Singapore, 2008 |
| [2] | Li Shujun, Zhang Zhe, Li Huiwen, et al.Research on Compilation of Nautical Charts of Arctic Regions[J]. Hydrography and Charting, 2012,32(1):58-60(李树军, 张哲, 李惠雯,等.编制北极地区航海图有关问题的探讨[J] . 海洋测绘,2012,32(1):58-60) |
| [3] | Zhao Hu, Li Lin, Gong Jianya. Universal Map Projection Selection[J]. Geomatic and Information Science of Wuhan University, 2010, 35(2):244-247(赵虎, 李霖, 龚健雅. 通用地图投影选择研究[J]. 武汉大学学报·信息科学版, 2010, 35(2):244-247) |
| [4] | Skopeliti A,Tsoulos L. Choosing a Suitable Projection for Navigation in the Arctic[J]. Marine Geodesy, 2013(2): 234-259 |
| [5] | Wen Chaojiang, Bian Hongwei, Wang Rongying,et al. Availability and Errors Analysis of Polar Stereographic Projection in Polar Navigation[J].Journal of Naval University of Engineering, 2014,26(3):42-47(温朝江,卞鸿巍,王荣颖,等.极区极球面投影的可用性及误差分析[J].海军工程大学学报,2014,26(3):42-47) |
| [6] | Ai Songtao, Wang Zemin, E Dongcheng,et al. Topographic Survey on the Surface of Glacier Auster Lovenereen and Pedersenbreen in Svalbard Based on GPS Method[J]. Polar Research, 2012, 24(1): 53-59 (艾松涛, 王泽民, 鄂栋臣, 等. 基于GPS 的北极冰川表面地形测量与制图[J]. 极地研究, 2012, 24(1): 53-59) |
| [7] | Beresford P C. Map Projection Used in Polar Regions[J]. Journal of Navigation, 1953,6(1):29-37 |
| [8] | Wang Qinghua, E Dongcheng, Chen Chunming, et al. Popular Map Projection in Antarctica and Their Application[J]. Chinese Journal of Polar Research, 2002,14(3): 226-233(王清华, 鄂栋臣, 陈春明, 等. 南极地区常用地图投影及其应用[J]. 极地研究, 2002,14(3): 226-233) |
| [9] | Ye Ziyang.The Projections &Navigation Grid in Polar Navigation Chars[J].Navigation,1999(4):113-116 (叶子扬. 极区航空投影及领航网格[J] .导航,1989(4): 113-116) |
| [10] | Li Guozao, Yang Qihe, Hu Dingquan. Map Projection[M]. Beijing: People's Liberation Army Press, 1993(李国藻, 杨启和, 胡定荃. 地图投影[M]. 北京:解放军出版社, 1993) |
| [11] | Hua Tang. Mathematical Foundation of Navigational Charts[R]. Navigation Gurantee Department of Naval Headquarters, Tianjin, 1985: 265-270(华棠.海图数学基础[R]. 海司航保部, 天津, 1985:265-270) |
| [12] | Naumann J.Grid Navigation with Polar Stereographic Charts[J]. European Journal of Navigation, 2011, 9(1):4-8 |
| [13] | Guo Deyin,Qu Shaobin,Jiang Lu, et al. A Practical Method of Locating at High Latitudes[J].Marine Technology,1999(4):16-19(郭德印, 曲少斌, 姜璐,等. 在高纬度地区确定船位的实用方法[J] . 航海技术, 1999(4):16-19) |
| [14] | General Administration of Quality Suppervision, Inspection and Quarantine of the Peole's Republic of China. Chinese Nautical Charts' Compilation Specification[S]. Beijing: Chinese Standard Press, 1999(国家质量监督检验检疫总局. 中国航海图编绘规范[S]. 北京: 中国标准出版社, 1999) |
 2015, Vol. 40
2015, Vol. 40


