文章信息
- 翟振和, 孙中苗
- ZHAI Zhenhe, SUN Zhongmiao
- Jason-2高度计数据在中国四大海域的波形重跟踪与分析
- Waveform Retracking Analysis of Jason-2 Altimeter Data in the Four Chinese Sea Area
- 武汉大学学报·信息科学版, 2015, 40(11): 1499-1503
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1499-1503
- http://dx.doi.org/10.13203/j.whugis20130707
-
文章历史
- 收稿日期: 2013-11-23

波形重跟踪(waveform retracking)是海洋测高卫星数据处理中的一项关键技术,对于获取高精度海面高、海浪高、风速等地球物理参数以及提高沿轨海面高数据分辨率具有重要作用。国内外学者利用重心偏移重跟踪算法(offset centre of gravity retracker)、β参数法、阈值法、改进阈值法等对T/P、ERS-1、Envisat、Geosat等测高卫星开展了波形重跟踪计算与分析,获得了大量有价值的结论和研究成果[1, 2, 3, 4, 5, 6, 7]。上述的波形跟踪算法大都基于经验函数,而实际上传统雷达测高卫星的回波波形可由Brown-Hayne模型进行表示,该模型基于雷达回波波形的物理特征给出了描述波形能量的卷积表达式[8, 9]。Jason-2卫星搭载了高性能的“海神-3”雷达高度计,其海面高测量精度在2 m有效波高、1 Hz采样条件下优于3.4 cm,其测量水平代表了目前国际先进水平,目前国内学者对Jason-2卫星方面的研究偏少。特别是在Brown-Hayne模型具体实现过程中,少有文献涉及到回波功率关于5个参数偏导数的推导,同时也缺乏在我国海域的计算分析。为此,本文将结合Jason-2的SGDR(sensor geophysical data record)数据对基于Brown-Hayne模型的波形重跟踪算法进行研究,同时与其他算法进行比较分析。
1 重心偏移重跟踪算法重心偏移重跟踪算法由Wingham算法发展而来,其目的是根据不同波形门数的能量水平获取每个波形的重心。波形的振幅A和宽度W以及波形重心对应的门位置COG表示为[10]:
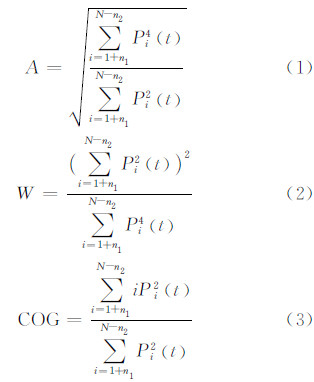
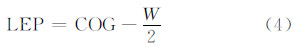
最后得到相对于正常跟踪点的距离改正值dr:
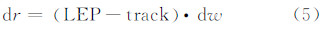
阈值重跟踪算法由Davis的研究发展而来[8],首先计算热噪声 PN:
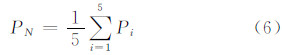
然后计算阈值水平Th:
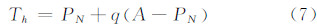

Brown-Hayne模型的基本形式如下:


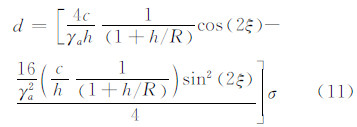
参数估计的方法有极大似然估计(MLE)、迭代最小二乘(ILS)等方法,本文采用迭代最小二乘法求解5个参数。通过参数估计可获得平均海水面对应的时间偏移参数t0,进而得到海面高的改正值。由于关于5个参数偏导数的推导和公式占用大量篇幅,本文将不直接给出这一过程以及具体公式。
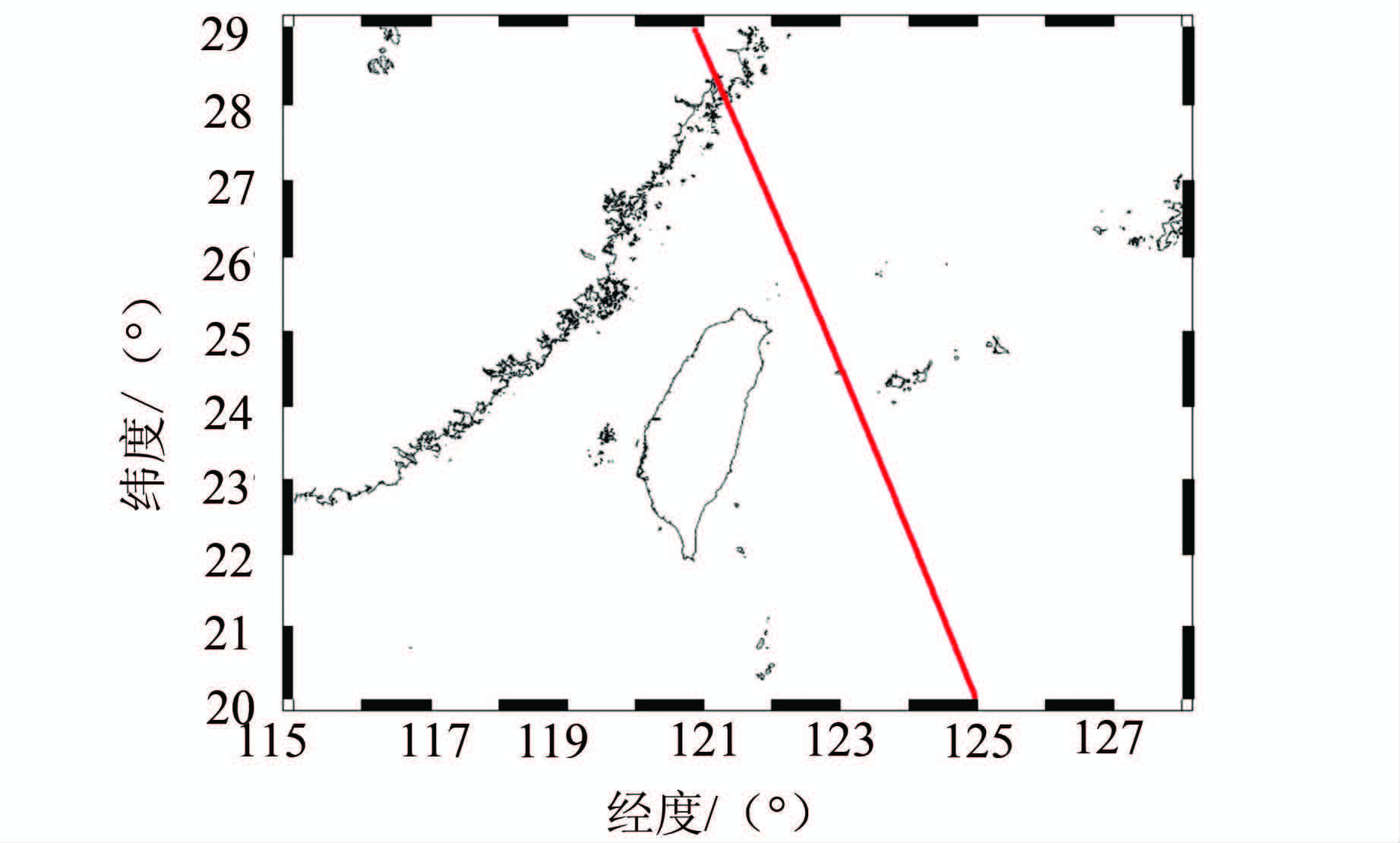
4 中国海域的试验与分析本文计算用的数据采用法国空间局(CNES)发布的Jason-2卫星SGDR数据,计算区域分别选择渤海、黄海、东海和南海。其中渤海(北纬38.2°~38.8°)、黄海区域(北纬35°~35.6°)采用第136周期编号“062”弧段的Ku波段20 Hz数据进行分析,该弧段测量数据的地面轨迹见图 1。东海区域(北纬25°~28°)采用的是第136周期编号“240”弧段的Ku波段20Hz数据,其地面轨迹见图 2。南海区域(北纬15°~19.5°)采用的是第136周期编号“114”弧段的Ku波段20 Hz数据,其地面轨迹见图 3。

|
| 图 1 Jason-2“062”弧段地面轨迹 Fig. 1 Jason-2“062”Pass Ground Track |
|
| 图 2 Jason-2“240”弧段地面轨迹 Fig. 2 Jason-2“240”Pass Ground Track |

|
| 图 3 Jason-2“114”弧段地面轨迹 Fig. 3 Jason-2“114”Pass Ground Track |
在最小二乘解算中,分别采用加权与不加权两种形式求解,加权的准则如下:

|
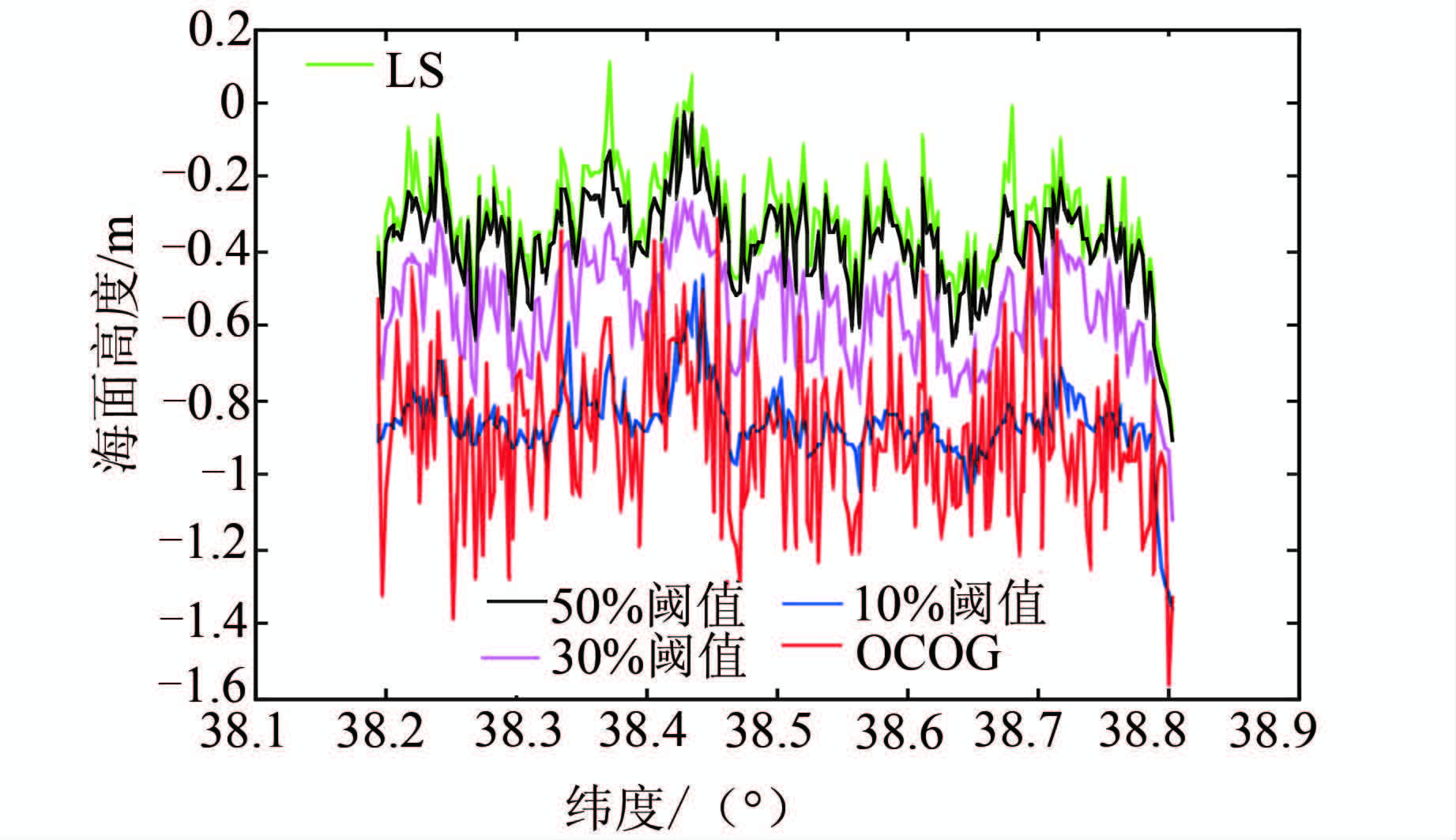
| 图 4 渤海区域的波形重跟踪结果 Fig. 4 Results of Waveform Retracking in Bohai Area |
|
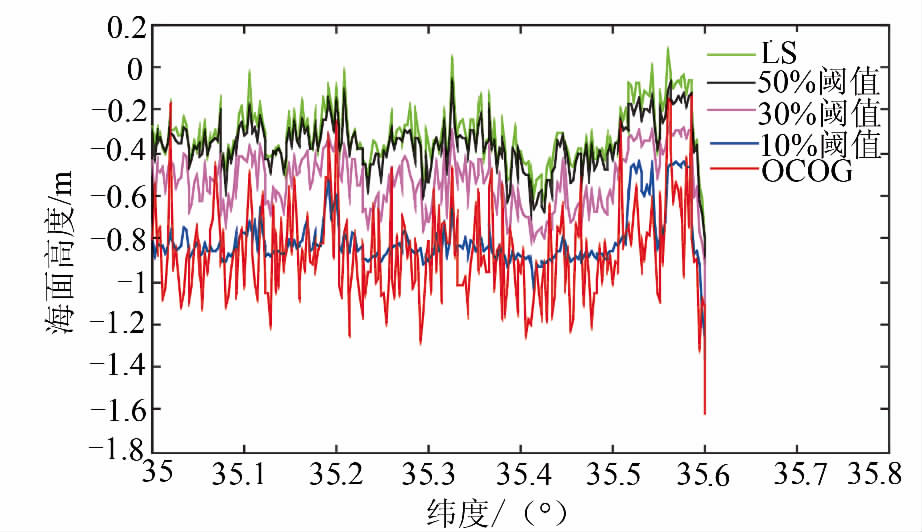
| 图 5 黄海区域的波形重跟踪结果 Fig. 5 Results of Waveform Retracking in Yellow Sea |

|
| 图 6 东海区域的波形重跟踪结果 Fig. 6 Results of Waveform Retracking in East China Area |

|
| 图 7 南海区域的波形重跟踪结果 Fig. 7 Results of Waveform Retracking in South China Area |
计算结果表明,加权与不加权结果非常一致,图 4~图 7表示的即不加权的结果,从图 4~图 7中可以看出,50%阈值算法与最小二乘算法(迭代4次)得到的结果最为接近,而其他算法则表现出较大的差异,为了验证算法的准确性,将50%阈值算法与最小二乘算法结果与最大似然估计法结 果(由法国空间局公布)进行比较,见表 1~表 2。
| 区域 | 最大差值 | 最小差值 | 差值均值 | 标准偏差 |
| 渤海区域 | 0.21 | -0.27 | -0.05 | 0.05 |
| 黄海区域 | 0.12 | -0.18 | -0.04 | 0.03 |
| 东海区域 | 0.22 | -0.38 | -0.10 | 0.06 |
| 南海区域 | 0.15 | -0.31 | -0.07 | 0.04 |
| 区域 | 最大差值 | 最小差值 | 差值均值 | 标准偏差 |
| 渤海区域 | 0.10 | -0.06 | 0.01 | 0.02 |
| 黄海区域 | 0.16 | -0.16 | 0.00 | 0.02 |
| 东海区域 | 0.12 | -0.11 | 0.02 | 0.03 |
| 南海区域 | 0.14 | -0.13 | 0.01 | 0.02 |
表 1、表 2结果表明在阈值算法中,50%阈值相比较于其他阈值及OCOG算法更优,但存在4~10 cm的偏差。基于Brown-Hayne模型的最小二乘估计法与最大似然估计法(MLE)得到的结果最为一致,比较精度约2 cm左右,考虑到MLE算法本身存在一定的误差,因此,基于Brown-Hayne模型的最小二乘估计法在实用中是准确可行的。在渤海、黄海两个海域,利用Brown-Hayne模型获得的海面高改正量平均在30 cm左右,东海区域改正量略大于渤海、黄海,南海部分海域(如北纬16°~17°)其改正量超过50 cm,有的甚至达到1 m,经过分析这部分海域正好位于西沙群岛海域。综合4个海域的结果可以看出,越靠近大陆、岛屿,波形重跟踪的改正量越大,这说明在靠近大陆及岛屿区域要获得精确的海面高,波形重跟踪的作用尤为重要。
5 结语本文对Brown-Hayne模型法、OCOG算法、阈值算法3种波形重跟踪算法进行了研究分析,利用Jason-2卫星的SGDR数据在中国渤海、黄海、东海、南海4个海域开展了波形重跟踪试验,得到以下有益的结论。
1) 在渤海、黄海、东海、南海4个海域,基于Brown-Hayne模型的最小二乘估计法获得的波形重跟踪结果相比较于阈值法、OCOG算法与法国空间局公布的最大似然估计法结果最为一致,经比较精度约2 cm左右。
2) 50%阈值算法获得的波形重跟踪结果相比较于其他阈值精度更优,经比较精度在3~6 cm,但存在4~10 cm的偏差。OCOG算法获得的结果存在较大误差,但其结果作为Brown-Hayne模型的初始值在实践中是可行的。
3) 在4个海域中,当地面轨迹靠近大陆时,海面高改正量会较宽阔海域增大。南海区域的海面高改正量最大,最大可至1 m,其原因可能是卫星地面轨迹经过了西沙群岛,雷达回波波形受到了一定的影响。
4) Brown-Hayne模型是描述传统雷达高度计的基本回波模型,基于该模型的重跟踪算法显然比OCOG法、阈值法两种经验算法更加严密和准确,但Brown-Hayne模型在使用中较为复杂,为了提高计算速度,在精度要求不高的情况下,阈值算法不失为另一种选择。
致谢:感谢中国科学院空间中心的许曦煜、杨双宝在本文撰写中给予的帮助。
| [1] | Bao Lifeng, Lu Yang, Xu Houze. Waveform Retracking Method of Topex/Poseidon Satellite in Shallow Sea[J]. Chinese J Geophys, 2004, 47(2):216- 221(鲍李峰, 陆洋, 许厚泽.浅海区域Topex/Poseidon 测高卫星数据波形重构方法[J].地球物理学报, 2004, 47(2):216- 221) |
| [2] | Chang Xiaotao, Li Jiancheng, Guo Jinyun.A Multi-Leading Edge and Multi-Threshold Waveform Retracker[J]. Chinese J Geophys, 2006, 49(6):1 629-1 634(常晓涛, 李建成, 郭金运, 等.一种多前缘多阈值的波形重构算法[J].地球物理学报, 2006, 49(6):1 629-1 634) |
| [3] | Yang Le, Lin Minsen, Zhang Youguang.et al. The Research of Waveform Retracking of JASON-1 in Chinese Coastal Area[J]. Acta Oceanologica sinica, 2010, 32(6):91-101(杨乐, 林明森, 张有广, 等.中国近岸海域高度计JASON-1测量数据的波形重构算法研究[J].海洋学报, 2010, 32(6):91-101) |
| [4] | Guo Jinyun, Gao Yonggang, Chang Xiaotao, et al. The Threshold Optimized Algorithm of ENVISAT Waveform Retracking in Coastal Area[J]. Chinese J Geophys, 2010, 53(4):807-814(郭金运, 高永刚, 常晓涛, 等.近岸海域ENVISAT卫星测高波形重定的Threshold优化算法[J].地球物理学报, 2010, 53(4):807-814) |
| [5] | Yang Yuande, E Dongchen, Huang Jinwei, et al.Chinese Coastal Gravity Anomalies from Waveform Retracked Geosat/GM Altimetry[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12):1 288-1 290(杨元德, 鄂栋臣, 黄金维, 等.Geosat/GM波形重跟踪反演中国沿海区域重力异常[J]. 武汉大学学报·信息科学版, 2008, 33(12): 1 288-1 290) |
| [6] | Chu Yonghai, Li Jianchen, Zhang Yan, et al. Analysis and Investigation of Waveform Retracking Data of ENVISAT[J]. Journal of Geodesy and Geodynamics, 2005, 25(1):77-79 (褚永海, 李建成, 张燕, 等. ENVISAT测波形重跟踪分析研究[J].大地测量与地球动力学, 2005, 25(1):77-79) |
| [7] | Guo Jinyun, Chang Xiaotao, Sun Jialong.et al. Waveform Retracking of Satellite Radar Altimeter and Apllications[M]. Beijing:Press of Surveying and Mapping, 2013(郭金运, 常晓涛, 孙佳龙, 等. 卫星雷达测高波形重定及应用[M].北京:测绘出版社, 2013) |
| [8] | Davis C H. A Robust Threshold Retracking Algorithm for Measuring Ice-Sheet Surface Elevation Change from Satellite Radar Altimeter[J]. IEEE Trans Geosci Remote Sensing, 1997, 35(4):974-979 |
| [9] | Lee Hyongki, Shum C K, William Emery. Validation of Jason-2 Altimeter by Waveform Retracking over Coastal Ocean[J]. MarineGeodesy, 2010, 33:304-316 |
| [10] | Hwang C, Guo Jinyun. Coastal Gravity Anomalies from Retracked Geosat Altimetry:Improvement, Limitation and the Role of Airborne Gravity Data[J]. J Geod, 2006, 80:204-216 |
| [11] | Vignudelli S, Kostianoy A, Cipollini P.Coastal Altimetry[M]. Berlin, Heidelberg: Springer-Verlag, 2011:81-83 |
| [12] | Deng X, Featherstone W E.A Coastal Retracking System for Satellite Radar Altimeter Waveforms: Application to ERS-2 Around Australia[J]. Journal of Geophysical Research, 2006, 111(6):1-16 |
 2015, Vol. 40
2015, Vol. 40


