文章信息
- 徐晓华,郭金城,罗佳
- XU Xiaohua,GUO Jincheng,LUO Jia
- 利用COSMIC掩星资料分析大气重力波参数的全球分布特征
- Analysis of the Global Distribution of the Atmospheric Gravity Wave Parameters Using COSMIC Radio Occultation Data
- 武汉大学学报·信息科学版,2015,40(11): 1493-1498
- Geomatics and Information Science of Wuhan University,2015,40(11): 1493-1498
- http://dx.doi.org/10.13203/j.whugis20130587
-
文章历史
- 收稿日期: 2014-05-18

重力波是大气中最基本的动力过程,从微尺度到天气尺度的多种大气现象都和重力波有非常密切的联系,大气重力波对全球大气环流及大气的动力学、热力学结构都有着重要影响[1]。用于预报的大气环流模式(general circulation models,GCMs)需对重力波进行参数化,但仍缺乏对重力波参数化的观测值约束[2]。通过观测手段获得重力波的相关参数将有助于提高模式预报的精度和可靠性。
国内外对重力波进行了诸多研究[1, 2, 3, 4, 5],通过实测数据的温度廓线和风速廓线获取重力波的势能(potential energy,Ep)、波长及传播方向、动量通量(momentum flux,MF)等参数是领域内的研究热点。Ern等[4]首次利用CRISTA卫星数据获取重力波水平波长和MF绝对值的全球估值。
自20世纪末,利用GPS无线电掩星技术(radio occultation,RO)探测地球大气状态受到越来越多的关注。GPS掩星探测已成为全球大气探测的重要方式。利用GPS掩星资料进行重力波研究的工作主要集中在由掩星温度廓线提取重力波Ep及垂直波长并进行相关分析[2, 5],而由掩星温度廓线进行重力波水平波长和动量通量MF的研究成果则相对较少。Wang等[2]借鉴Ern等[4]的方法,首次从GPS RO数据提取了重力波的水平波长和MF。Faber等[6]基于Wang等[2]的方法,使用连续小波分析提取温度扰动,提出了三角配对法则提取重力波的水平波长和MF。该方法不涉及超定方程求解,且结果的空间分辨率更高。但连续小波分析参数设置复杂,其时频谱的相位信息是相对于局部时域的,不利于定量提取信号信息。
鉴于国内目前利用GPS RO数据进行重力波研究的成果少见,本文首先对从单一温度廓线提取重力波相关参数的方法进行了详细介绍。与小波变换相比,S变换具有无损可逆性且是一种线性时频表示,不存在交叉项的干扰,同时S变换中含有小波变换不具备的相位因子[7]。因此,与Faber等[6]的方法有所不同,本文在温度扰动的提取中使用S变换分析处理。基于此方法,利用COSMIC RO 2007~2008年干温廓线数据,分析了2007~2008年夏季和冬季20~30 km大气层重力波的相关参数在全球的分布和季节变化特征;并与国内外已有结果进行了对比,分析了不同研究成果存在差异的可能原因。
COSMIC是2006年美国和中国台湾地区合作发射的地球大气探测系统,由6颗低轨卫星组成。COSMIC每天可提供约2 000~2 500次全球掩星事件,温度廓线可覆盖5~40 km高度大气,其垂直分辨率在平流层约为1 km,在低对流层约为100 m,其水平分辨率为100~200 km,温度廓线的精度约为±5 K[8]。COSMIC数据分析和存储中心(COSMIC Data Analysis and Archive Center,CDAAC)为科学研究提供精确有效的后处理产品。由于10 km以上大气中水汽含量极少,10~35 km范围内的COSMIC干温廓线可直接作为真实大气的温度廓线[8]。本文使用CDAAC提供的2007~2008年夏季(6~8月)和冬季(12月及次年1~2月)COSMIC后处理干温廓线(Version2010.2640)分析重力波活动的全球分布及季节变化。
1 原理与方法在中层大气动力学特征的描述中,重力波水平动量的垂直通量(简称动量通量)MF是一个关键量。MF与势能Ep的关系详细推导可参考文献[4]等,在中频近似下,MF与Ep的关系如下:
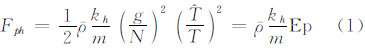
 是重力波的温度振幅;kh是水平波数;m为垂直波数;g为重力加速度; 是背景大气密度;N为浮力频率;T为温度。
1.1 提取温度扰动T′
是重力波的温度振幅;kh是水平波数;m为垂直波数;g为重力加速度; 是背景大气密度;N为浮力频率;T为温度。
1.1 提取温度扰动T′
根据重力波线性理论[1],实际测量得到的大 气温度廓线T( z )由背景温度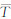 z 和温度扰动T′( z )组成,T′ z =T (z) -
z 和温度扰动T′( z )组成,T′ z =T (z) -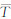 z 。温度扰动廓线的提取在重力波参数计算过程中极为重要,传统的滤波或拟合的方法得到的温度扰动廓线中仍含有较强的背景温度信息。
z 。温度扰动廓线的提取在重力波参数计算过程中极为重要,传统的滤波或拟合的方法得到的温度扰动廓线中仍含有较强的背景温度信息。
本文借鉴文献[2]的方法提取温度扰动廓线。首先,将COSMIC的单天温度廓线数据在8~38 km范围以0.25 km等间隔内插,然后对内插数据按照15°×10°(经度×纬度)格网化得到纬向平均温度廓线。其次,对纬向平均温度序列运用S变换,提取0~6纬向波数信息,对其运用S逆变换得到各格网的纬向背景温度;将此背景温度看作纬度和高度的函数,并且依据经度将背景温度插值到格网中的实际温度廓线处,得到每条温度廓线对应的背景温度廓线。最后,将原温度廓线与背景温度廓线的差作为温度扰动廓线。关于S变换文献[7]有详细介绍,本文不再赘述。
1.2 计算 Ep从温度廓线提取出背景温度和温度扰动后,可由式(2)、式(3)计算得到重力波的势能Ep。

S变换得到的时频谱的频率域与输入数据的长度有较大关系,本文在计算20~30 km高度区间内的重力波参数时,仍然将8~38 km范围内的温度扰动廓线作为输入,但只关注S变换的时频谱中20~30 km高度区间内的时频信息。在20~30 km高度内的所有数据点上均计算重力波的垂直波长 λk,利用S变换频谱中对应数据点的振幅值Ak对λk进行加权平均,得到20~30 km高度区间内的重力波垂直波长平均值λ,即λ=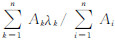 ,而m=2π/λ。
,而m=2π/λ。
Ern等[4]利用CRISTA数据,使用式(4)得到了重力波水平波数的估值:
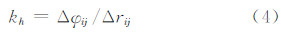

由于低层大气中重力波的活动在夏季和冬季达到峰值,同时为便于和已有成果比较,本文选取2007和2008年夏季及冬季的COSMIC干温廓线数据,计算高度为20~30 km大气层重力波的势能Ep、水平波长λH与垂直波长λV、动量通量MF的绝对值,对每天单条廓线计算的20~30 km范围内重力波各参数值取该高度范围内的平均,从而得到各参数单天的全球分布,对各季节多天的计算结果,以5°×5°的格网间隔求取重力波各参数的均值作为最终结果。由于超过75°的高纬地区掩星廓线数较少,故所有参数在南北纬75°以外区域的结果均没有显示。结果图中所示夏季、冬季均针对北半球。为图示方便,波数转换为波长后给出。
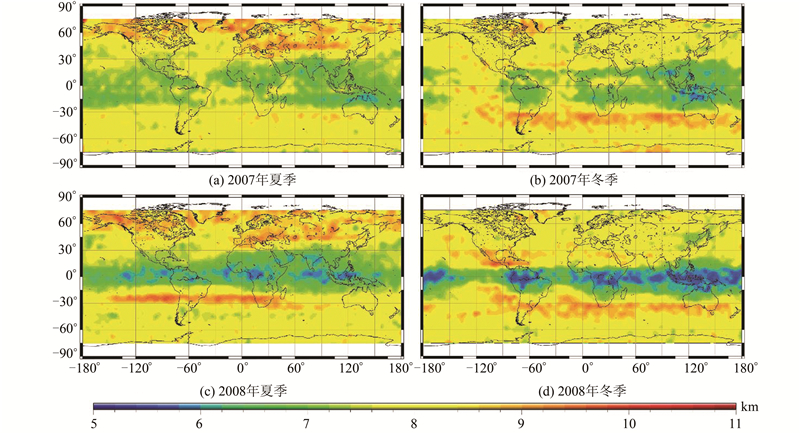
图 1给出了2007~2008年夏季和冬季20~30 km大气中重力波λV时空均值的全球分布。在20~30 km高度λV基本上介于5~11 km,其值整体上沿纬向分布,并由赤道向两极递增。对比2007年和2008年夏季、冬季的结果,λV低值都主要出现在热带,而高值主要出现在夏半球的高纬地区;2007年热带的低值范围比2008年的宽,但2008年热带出现接近5km低值的区域更多。
|
| 图 1 2007年和2008年夏季、冬季重力波垂直波长全球分布 Fig. 1 Global Distribution of Gravity Wave Vertical Wavelength in NH Summer and NH Winter of 2007 and 2008 |
图 2是2007~2008年夏季和冬季20~30 km大气中重力波λH全球分布图,由于受COSMIC数据目前的水平分辨率限制,且从单一温度廓线提取λH的方法基于中频近似假设,故得到的λH量级都较大。图 2显示的λH介于1 000~5 000 km。整体上λH高值主要出现在热带区域。对比2007、2008年夏季和冬季结果,与λV不同,λH并不呈纬向分布规律。但λH的高值主要出现在夏半球的 陆地区域和冬半球的海洋区域;特别是北半球,其陆地区域λH夏季和冬季的变化很明显,说明北半球陆地区域重力波夏季比冬季活跃。北半球主要被陆地覆盖,而南半球主要是海洋覆盖,地形作用和明显的季节性对流变化可能导致南北半球冬夏两季重力波活动的差异。对比分析图 2,北半球的重力波主要来源于地形作用,南半球则主要来源于对流作用。图 3给出了2007~2008年夏季和冬季20~30 km大气中重力波Ep的全球分布,整体上Ep值呈现由赤道向两极递减的分布特征,其分布在中低纬度区域具有沿赤道对称的特点。数值大于5 J/kg的Ep高值主要对称分布于赤道附近,当北半球处于冬季时这种分布格局中超过10 J/kg的区域更广,说 明北半球处于冬季时赤道附近重力波较之夏季时更活跃,这可能与赤道附近的对流活跃有关。而小于5 J/kg的Ep值则呈现明显的季节分布特征,夏半球高纬地区其值几乎为零,而冬半球的高纬度地区Ep值仍在4 J/kg左右。文献[5]研究表明,在目前的数据观测条件下,在分布格局上比较重力波参数结果更有意义;由于不同方法使用的数据和涉及滤波、时空平均等处理细节方面存在差异,最后的结果在数值上可能不完全一致。已有研究成果[2, 4, 6]表明,Ep的高值主要分布在赤道附近和冬半球的中高纬区域,与本文符合较好,即中高纬度区域Ep的分布具有明显的季节性差异,而Ep高值在热带地区沿赤道对称分布。

|
| 图 2 2007年和2008年夏季、冬季重力波水平波长全球分布 Fig. 2 Global Distribution of Gravity Wave Horizontal Wavelength in NH Summer and NH Winter of 2007 and 2008 |

|
| 图 3 2007年和2008年夏季、冬季重力波势能(Ep)全球分布 Fig. 3 Global Distribution of Gravity Wave Potential Energy (Ep) in NH Summer and NH Winter of 2007 and 2008 |
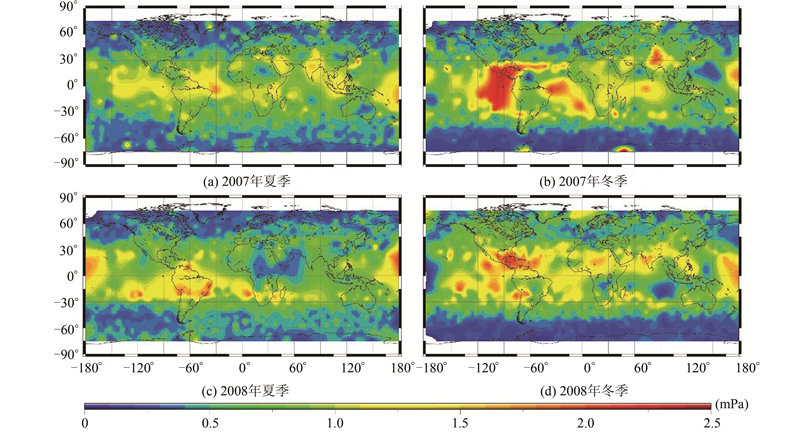
图 4是2007~2008年夏季和冬季20~30 km大气中重力波MF绝对值的全球分布,整体上MF呈现沿赤道对称的特点,且数值由赤道向两极逐渐递减,夏半球高纬区域MF值几乎为零。北半球处冬季时MF的高值范围更广,说明冬季全球重力波更为活跃,图 3中Ep的全球分布也体现了这一特征。在美洲大陆西面海域MF的值都较高,当北半球值冬季时更明显;而美洲大陆的西岸有绵延的科迪勒拉山系,MF的这种分布特征可能是山脉地形主导了这一区域的重力波活动。结合图 3和图 4,各年各季节赤道地区Ep和MF值均很高,可能该区域较强的对流作用导致了重力波频繁活动;另外,掩星数据分布在赤道较中纬度地区稀疏,因此带来的采样误差也可能导致了结果的偏差。式(5)表明重力波MF的绝对值主要由重力波水平波长、垂直波长、Ep计算得到,但图 3和图 4中Ep和MF的全球分布格局较为一致,说明由COSMIC干温廓线计算的重力波MF绝对值的分布格局主要受Ep影响,水平波长、垂直波长的分布对最终结果影响较小。
|
| 图 4 2007年和2008年夏季、冬季重力波动量通量(MF)绝对值全球分布 Fig. 4 Global Distribution of Gravity Wave Absolute Momentum Flux (MF) in NH Summer and NH Winter of 2007 and 2008 |
图 3中Ep高值主要分布于热带,图 4中MF高值也主要集中在热带区域,这表明20~30 km高度重力波的活动较活跃区主要集中在热带区域。文献[3]利用TIMED卫星上SABER温度剖面8年数据研究重力波的温度振幅也揭示了同样的重力波活动分布特征。而文献[9]利用HIRDLS、SABER数据研究水平波长小于1 000 km的重力波活动,得到MF绝对值主要与重力波的垂直波长分布格局一致,即MF的高值主要分布于中纬度和高纬度区域,MF的峰值则分布于南半球的高纬度区域。文献[9]的结果与本文结果的差异,说明不同水平波长的重力波活动在全球的分布有较明显差异。这种差异,也可能由COSMIC和SABER、HIRDLS的温度数据的时空分辨率、温度测量方式及其精度等数据本身的差异所导致;具体研究涉及的重力波波谱范围、大气高度、背景温度提取方法和滤波选择等数据处理细节也有影响;另外卫星的视线与重力波传播方向的夹角也可能对最终结果产生影响。笔者后续将会对此展开进一步研究。
3 结语本文利用COSMIC 2007~2008年的干温廓线提取了20~30 km大气中重力波的相关参数并最终计算了重力波动量通量MF的绝对值,分析了这些参数值的全球分布和季节变化特征。结果与国际上已有的一些研究结果基本一致,说明利用掩星数据研究重力波是完全可行的。目前的GPS掩星数据,受限于其较差的水平分辨率,只能用于研究大气中水平波长较长(大于1 000 km)的重力波活动,同时也只能提取MF的绝对值,无法获得重力波的传播方向。但是随着COSMIC-Ⅱ等新一代掩星任务的实施,同时增加对GALILEO、GLONASS和北斗导航系统的掩星观测,单天掩星事件数将会大幅增加。届时完全可以由掩星数据提取重力波MF矢量,掩星资料将为大气重力波研究发挥更大作用。
致谢:衷心感谢CDAAC提供的COSMIC大气干温廓线数据。
| [1] | Fritts D C, Alexander M J. Gravity Wave Dynamics and Effects in the Middle Atmosphere[J]. Reviews of Geophysics-Richmond Virginia then Washington, 2003, 41(1): 3-64 |
| [2] | Wang L, Alexander M J. Global Estimates of Gravity Wave Parameters from GPS Radio Occultation Temperature Data[J]. Journal of Geophysical Research: Atmospheres, 2010, 115(D21): 122-134 |
| [3] | Zhang Yun, Xiong Jiangang, Wan Weixin. Analysis on the Global Morphology of Middle Atmospheric Gravity Waves[J]. Chinese Journal of Geophysics, 2011, 54(7):1 711-1 717(张云, 熊建刚, 万卫星. 中层大气重力波的全球分布特征[J]. 地球物理学报, 2011, 54(7): 1 711-1 717) |
| [4] | Ern M, Preusse P, Alexander M J, et al. Absolute Values of Gravity Wave Momentum Flux Derived from Satellite Data[J]. Journal of Geophysical Research: Atmospheres, 2004, 109(D20):103-120 |
| [5] | Luna D, Alexander P, de la Torre A. Evaluation of Uncertainty in Gravity Wave Potential Energy Calculations Through GPS Radio Occultation Measurements[J]. Advances in Space Research, 2013, 52(5): 879-882 |
| [6] | Faber A, Llamedo P, Schmidt T, et al. A New Approach to Global Gravity Wave Momentum Flux Determination from GPS Radio Occultation Data[J]. Atmospheric Measurement Techniques Discussions, 2013, 6: 2 907-2 933 |
| [7] | Stockwell R G, Mansinha L, Lowe R. Localization of the Complex Spectrum: The S Transform[J]. Signal Processing, IEEE Transactions on, 1996, 44(4): 998-1 001 |
| [8] | Horinouchi T, Tsuda T. Spatial Structures and Statistics of Atmospheric Gravity Waves Derived Using a Heuristic Vertical Cross-Section Extraction From COSMIC GPS Radio Occultation Data[J]. Journal of Geophysical Research: Atmospheres, 2009, 114(D16): 110-124 |
| [9] | Geller M A, Alexander M J, Love P T, et al. A Comparison Between Gravity Wave Momentum Fluxes in Observations and Climate Models[J]. Journal of Climate, 2013, 26(17):6 383-6 405 |
 2015,Vol. 40
2015,Vol. 40



