影响卫星定轨精度的因素包括数据处理方法、观测量精度以及力学模型精度^{[1, 2]}。目前，数据处理方法日趋成熟^{[3, 4, 5]}，观测量精度也在不断提高^{[6, 7]}，但是，由于对某些摄动力的物理机制认识不足，力学模型的缺陷正在成为限制卫星精密定轨精度进一步提高的主要因素^[8]，例如GPS等导航卫星的光压模型^[9]、LEO卫星的大气阻力模型^[10]等。

提高力学模型精度的方法大体上可分为以下两类：① 分析摄动力物理机制，对摄动力进行更高精度的建模；② 对不完善的力学模型进行一定的补偿。前者治本，但是较难实现；后者虽仅是治标，不过借助一定的数学方法更易实现，此外，通过补偿的方法提高定轨精度，反之也有助于对摄动力的物理机制进行更深入的分析。文献[11]提出以随机型的力学方程代替确定型的力学方程；文献[12]提出以傅里叶级数来近似未知力，文献[13]以级数展开为基础构建了ECOM光压模型^{[14, 15]}；文献[16]提出以经验加速度弥补力学模型的不足；文献[17]在星载LEO精密定轨中对比了几种不同经验加速度模型的实际应用效果。在所有这些力学模型补偿方法中最常用的是附加伪随机脉冲的方法。

该方法最初是由Beutler等于1994年提出，并首先应用于GPS卫星精密定轨^[13]，而后拓展到星载LEO卫星精密定轨^{[8, 17]}，其在弥补力学模型缺陷、提高轨道(特别是LEO轨道)精度方面发挥了重要作用。但是，这种方法通常需要引入较多的伪随机脉冲参数，如果用常规方法进行参数估计，将会涉及大维数法矩阵的求逆运算，严重影响处理效率。

鉴于此，本文在研究了伪随机脉冲特性的基础上，给出了一种针对伪随机脉冲的参数快速估计方法。这一方法利用伪随机脉冲的特性，借助参数预消除与回代的思想，有效地规避了对大维数法矩阵的求逆运算，能够较好地降低伪随机脉冲对参数估计效率的不利影响。在此基础上，本文以GRACE卫星(LEO)实测数据为例，考察了伪随机脉冲对力学模型的补偿作用，并验证了本文方法的正确性。

1 伪随机脉冲

顾名思义，“伪”是指伪随机脉冲发生的时刻是预先定义和可控的；“随机”是指伪随机脉冲具有先验协方差信息；“脉冲”是指伪随机脉冲是瞬间变量。伪随机脉冲的特点是在给定时刻定义瞬间卫星速度增量,其对卫星轨道的影响为：卫星位置在整个区间上连续，但是卫星速度在脉冲发生时刻产生跳变。设在 t_i时刻增加伪随机脉冲，大小为v_i、方向为e(t_i)，则其对卫星运动的影响可表示为：

式中，Δ(t－t_i)= 1，

在卫星精密定轨中，如果力学模型精度不足，而又难以建立新的更高精度的力学模型，则通常会在原有力学模型的基础上，以一定时间间隔沿特定方向(通常为轨道的径向、切向和法向)增加估计伪随机脉冲，从而达到在一定程度上弥补力学模型缺陷的目的。伪随机脉冲的时间间隔与卫星受力特点有关，例如LEO卫星通常每十几分钟就要估计一组伪随机脉冲，仅处理1 d弧段的数据，就需要估计近百组的伪随机脉冲参数。

本文首先介绍了利用常规最小二乘方法估计伪随机脉冲的基本原理，在此基础上，给出了一种伪随机脉冲的快速参数估计方法。

2 常规最小二乘方法

为讨论问题方便，这里首先假设定轨中的待估参数仅包括6个密切轨道元素 和n个伪随机脉冲。在定轨弧段[t₀,t_n]中，以附加伪随机脉冲的历元t_i,i=1,…,n－1为界，将整个定轨弧段分成n+1个区间。在区间[t_i,t_i+1)上，经线性化的观测方程可表示为：

式中，t_l∈[t_i,t_i+1)表示观测历元；r₀(t_l)表示t_l时刻的卫星位置向量，由给定初值的卫星运动微分方程积分获得；o (r₀(t_l)) 表示观测函数；E_k表示参考时刻的密切轨道元素，ΔE_k为对应初值的改正量；Δv_mj表示附加的伪随机脉冲，m标识伪随机脉冲的个数，j标识伪随机脉冲的分量；ΔΦ_l表示t_l时刻观测量实测值与理论值之差，即O-C；ε_l表示观测噪声。

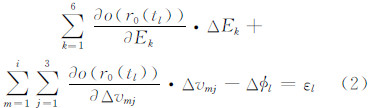
进一步，有:

其中，

为t_l时刻状态转移矩阵的第k列元素，通过求解变分方程获得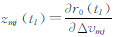为t_l时刻参考轨道位置关于伪随机脉冲的偏导数，可以证明其满足变分方程，由偏微分方程相关理论^{[18, 19]}可知：z_mj(t)可以表示为z_k(t)元素的线性组合，则有：

式中，系数β_mj,k的求取按照式(6)获得：

式中，e _mj表示伪随机脉冲的方向向量。

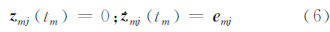
将式(4)和式(3)代入式(2)，有：

进一步地，将式(7)表示为矩阵形式，则在区间 [t_i,t_i+1)中，观测方程可表示为：

其中，

至此，可以按照常规最小二乘方法，利用n+1个区间中的所有观测方程，直接进行参数估计。然而，为了提高定轨精度，通常附加的伪随机脉冲数量较多，如果直接按照以上方法进行参数估计，会涉及大维数矩阵求逆等问题，严重影响计算效率。针对这一问题，这里给出一种快速参数估计方法，其基本思路是利用伪随机脉冲的历元参数特性，借助参数预消除和回代的方法对伪随机脉冲进行估计。

3 快速参数估计方法

设区间[ t_i－1,t_i) 到 [t_i,t_i+1) 的密切元素改变是由3个伪随机脉冲Δv_ij,j=1,2,3引起的，则有：

其矩阵形式，可表示为:

由式(10)得： Δ E _i－1= I ₆ － B _i · Δ E _iΔ

假定截止t_i历元，所有观测量形成的法方程系统可表示为：

其中， 当i=1时，有：

当i>1时，有：

式中，N _i－2^*与 b _i－2^*的定义参见式(20)和式(21)。

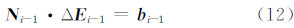
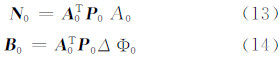
将式(11)代入式(12)，并在等式两端乘以 I ₆ － B _i ^T，得：

式(17)是高效算法的关键所在，只有进行如上的参数转换，才有可能对伪随机脉冲进行预消除。考虑伪随机脉冲的先验约束，式(17)变为：

其中，[B _i^T N _i－1 B _i ′= B _i^T N _i－1 B _i+ W 。

在式(18)中，对伪随机参数进行预消除，得：

其中，

利用式(13)~式(16)及式(20)和式(21)，对法方程式(12)进行更新，直到i=n。注意：不必在t_n历元建立伪随机脉冲Δ v _n，因此有:

可见，在求取Δ E _n－1的过程中，虽然可以同时获得Δ E _i,i=0,1,…,n－2，但是无需对其进行显式求取，因为这些中间结果事实上仅是基于区间 [t₀,t_i+1) ,i=0,1,…,n－1上相应观测数据的滤波结果，而并不是基于所有观测数据的最终估值，其精度必然受限。正确的求解方法如下：在获得Δ E _n－1之后，启动回代过程，根据式(18)，有：

其中，i=n－1；Δ E _i由式(22)获得；其他各项已经在求取Δ E _n－1的过程中获得。

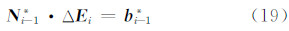
至此，我们可以获得Δ E _n－1和Δ v _n－1的估值，而后，利用式(11)可获得Δ E _n－2的估值，再根据式(23)获得Δ v _n－2的估值。如此叠代，直到获得初始密切元素Δ E ₀和所有附加伪随机脉冲Δ v _i,i=1,…,n－1的估值。

可以证明，利用以上方法获得的参数估值与常规最小二乘方法在数值上完全相同，而本文方法有效地规避了大维数法矩阵的组建和求逆，其计算效率要远高于传统方法。此外，实际应用中，还涉及模糊度等其他参数^[20]，我们只要将所有参数进行分组：① 不需要进行预消除的参数；② 需要进行预消除的参数。而后，对原来的Δ E _i和Δ v _i参数进行扩展，得到Δ_i和Δ_i，即可参照以上算法进行参数估计。

4 算例分析

这里首先验证本文方法的正确性，选取2013-05-13 GRACE A卫星1 d的GPS双频观测数据，采样间隔10 s，进行定轨实验。GRACE A卫星是2002年发射升空的一颗LEO卫星，其与GRACE B卫星相互配合共同完成高精度重力场的测量任务^[21]。为了便于对比分析，实验中采用以下两种方案进行定轨处理，并将所得到结果与JPL提供的事后精密星历进行对比，以评估定轨精度。

方案1  利用经典动力学方法进行LEO定轨，但在力学模型中不考虑大气阻力，数据处理策略见表 1。

方案2  在方案1处理策略的基础上，每15 min在径向、切向和法向附加一组伪随机脉冲，共96组伪随机脉冲，分别采用常规最小二乘方法和本文方法进行参数估计。

图 1给出了方案1和方案2径向(R)、沿迹(T)和法向(N)的定轨误差变化情况，表 2对定轨结果进行了统计。由于方案2中常规最小二乘方法与本文方法所得结果完全相同，所以图 1和表 2中方案2仅以一种结果作为代表。

由图 1可见，由于没有考虑大气阻力，方案1中动力法定轨精度受限，仅在dm量级，特别地，由于大气阻力主要影响在沿迹方向，导致这一方向的精度明显低于其他方向；方案2中附加伪随机脉冲之后，R、T、N方向定轨精度都得到了不同程度的提高，特别是沿迹方向精度的改善最为明显。

由表 2可见，附加伪随机脉冲之后，R、T、N方向定轨精度分别由0.148 m、0.450 m、0.148 m提高到0.083 m、0.065 m、0.051 m，T方向精度得到较大幅度改善，基本达到了与R、N方向相当的精度水平。

以上结果表明，伪随机脉冲能够很好地弥补力学模型不完善对定轨精度的不良影响，利用本文方法能够实现对伪随机脉冲的正确有效估计。为了进一步说明本文方法在计算效率上的优势，取GRACE A卫星4 h和8 h两段弧段，分别按照1 min、2 min、3 min、5 min、6 min、9 min、10 min和15 min间隔增加伪随机脉冲参数，并按照常规最小二乘方法和本文方法同时进行参数估计，图 2给出了计算耗时的对比情况，图 3以R、T、N 等3个方向的平均RMS为精度指标给出了伪随机脉冲时间间隔的不同对定轨精度的影响情况。

由图 2结果可见，本文快速参数估计方法在计算效率上明显优于常规最小二乘方法，而且随着定轨弧长增长，常规方法计算耗时迅速增大，而本文方法却依然能够保持较高的计算效率。由图 3的结果可见，虽然利用本文方法能够以较高效率对伪随机脉冲进行参数估计，但是伪随机脉冲越密集，定轨精度并不一定越高。实际定轨中，应结合定轨弧长及卫星运动特点，附加适当数目的伪随机脉冲。此外，在一定范围内，定轨弧长越长，虽然需要消耗更多的计算时间，但是能够积累更多的观测信息，有助于定轨精度的提高，应该综合考虑精度和效率要求，选择适当的定轨弧长。

5 结语

本文研究了伪随机脉冲的特性，结合参数预消除与回代思想，给出了一种针对伪随机脉冲的参数快速估计方法，并利用星载GPS低轨卫星实测数据对相关方法进行了验证，结果表明,伪随机脉冲对弥补力学模型缺陷具有显著作用，本文给出的方法可以对伪随机脉冲进行正确有效的估计，结果与常规最小二乘方法精度相同，但相比常规最小二乘方法，本文方法在计算效率上具有明显优势。在力学模型不甚完善的条件下，利用本文方法，在精密定轨中附加适当数量的伪随机脉冲，能够在提高定轨精度的同时，显著改善计算效率。

特别需要指出的是，本文虽然以星载低轨卫星数据对算法进行实验验证，但是相关方法同样适用于导航卫星精密定轨，我国的北斗系统正处于建设发展初期，力学模型的研究完善还需要一个过程，在此条件下，利用适当的力学补偿方法以提高北斗卫星精密轨道精度，对北斗的推广应用具有重要意义，本文方法在北斗卫星精密定轨中的具体应用及实际效果，尚需作进一步的分析研究。