文章信息
- 季青, 庞小平, 赵羲, 程子桉
- JI Qing, PANG Xiaoping, ZHAO Xi, CHENG Zian
- 基于CryoSat-2数据的海冰厚度估算算法比较
- Comparison of Sea Ice Thickness Retrieval Algorithms from CryoSat-2 Satellite Altimeter Data
- 武汉大学学报·信息科学版, 2015, 40(11): 1467-1472
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1467-1472
- http://dx.doi.org/10.13203/j.whugis20150279
-
文章历史
- 收稿日期: 2015-05-05

2. 极地测绘科学国家测绘地理信息局重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Polar Surveying and Mapping, NASG, Wuhan 430079, China
海冰变化与全球和区域气候、生态系统和人类活动密切相关,海冰厚度是全球变化研究的重要参数。为精确预测气候的变化、海冰的物质平衡、海洋水循环及海洋-大气间的相互作用,迫切需要长时间序列的海冰厚度信息[1]。目前,各种方法被广泛应用于海冰厚度信息获取中[2-15],然而这其中只有卫星测高的方法可以连续获得半球尺度的海冰厚度信息[8]。
自2003年开始,许多学者利用卫星测高数据,通过 静力平衡方程模型,基于不同的算法和输入参数取值,估算了北极或南极海域的海冰厚度[6-15]。主要有Laxon03算法[6]、Kurtz09算法[9]、Yi11算法[11]和Laxon13算法[13]等。海冰上积雪厚度、海冰密度、积雪密度和海水密度是这4种算法共有的关键参数。这4种算法已多次被采用,本文主要探讨算法间的差异性及何种算法最优。
本文在分析海冰厚度估算算法的基础上,利用CryoSat-2卫星测高数据,估算这4种算法的海冰厚度并进行差异分析,再通过与高精度的IceBridge观测结果对比,尝试确定最优的估算算法及其模型参数。
1 基本原理与算法分析利用卫星测高数据估算海冰厚度的基本原理是通过卫星高度计,向海冰发射微波或激光脉冲,通过识别并获得海冰与邻近海水(冰间水道)的时间延迟,计算出海冰的出水高度(海冰水上部分高度),再根据静力平衡方程模型,附以必要的参数,估算出海冰的厚度[16]。计算公式为:
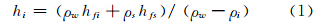
式中,ρw、ρi 和ρs分别为海水、海冰及海冰上积雪的密度;hfi为高度计测得的海冰出水高度;hfs 为海冰上积雪厚度。
由此可见,卫星测高方法估算海冰厚度的精度,除了与冰间水道识别的准确性密切相关外,还受算法模型参数(积雪厚度、海冰密度、积雪密度及海水密度)的影响。在实际应用中,不同算法的差异性主要体现在这两个方面。 Laxon03算法通过分析回波波形,以脉冲峰值(PP)为指标,来区分海冰和冰间水道,进而计算出海冰的出水高度;Kurtz09算法则借助雷达影像来识别冰间水道;Yi11算法将相对高(观测高与50 km平均高的差值)的最低2%平均值作为冰间水道的高程,计算海冰的出水高度;Laxon13算法改进了Laxon03算法,以高斯模型拟合回波波形,在原有PP指标的基础上,增加脉冲累积标准差(SSD)指标来识别冰间水道和计算出水高度。
此外,不同算法的输入参数取值或来源也不尽相同(表 1)。Laxon03算法使用了来源于实测的月度气象资料(以下简称W99)的积雪厚度和积雪密度[17]以及海冰密度和海水密度常数 (915 kg·m-3和1 024 kg·m-3)来估算海冰厚 度;Kurtz09算法等根据不同冰型(一年冰和多年冰)积雪厚度的不同,分别使用AMSR-E和W99积雪厚度;Yi11算法采用调整后的W99积雪厚度估算海冰厚度;Laxon13算法则对一年冰和多年冰分别赋予不同的海冰密度和积雪厚度取值,一年冰的积雪厚度采用W99中积雪厚度的一半来估算海冰厚度。
| 算法名称 | 海冰密度( ρ i)/(kg·m -3) | 积雪厚度( h fs) | 积雪密度(ρ s) | 海水密度(ρ w)/(kg·m -3) |
| 注:hfs(W99)为Warren气象资料中积雪厚度[17];hfs(AMSR-E+W99)为一年冰区AMSR-E积雪厚度,且多年冰区Warren气象资料中积雪厚度;hfs(W99/2+W99) 为一年冰区一半Warren气象资料中积雪厚度,且多年冰区Warren气象资料中积雪厚度;ρs(W99)为月度Warren气象资料中积雪密度; ρ′ s (W99)为根据文献[8]调整后的月度Warren气象资料积雪密度;FYI为一年冰;MYI为多年冰。 | ||||
| Laxon03 | ρ i = 915 | h fs = h fs(W99) | ρ s = ρ s(W99) | ρ w = 1 024 |
| Kurtz09 | ρ i = 915 | h fs = h fs(AMSR-E+W99) | ρ s = 320 kg\5m -3 | ρ w = 1 024 |
| Yi11 | ρ i = 915 | h fs = h fs(W99) | ρ s = ρ′ s (W99) | ρ w = 1 024 |
| Laxon13 | FYI:
ρ
i = 916.7
MYI: ρ i = 882.0 |
h fs = h fs(W99/2+W99) | ρ s = ρ s(W99) | ρ w = 1 024 |
采用不同算法和不同模型参数,会造成不同学者不同研究期海冰厚度估算结果的不可比性,因而,需要开展海冰厚度卫星测高估算算法的比较及其优选研究。
2 数据来源与研究区本文使用的估算海冰厚度的数据主要包括来源于欧洲空间局(ESA)的2011-03的CryoSat-2卫星测高数据(http://www.esa.int/Our_Activities/Observing_the_Earth/The_Living_Planet_Programme/Earth_Explorers/CryoSat-2)、来源于美国冰雪数据中心(NSIDC)的AMSR-E积雪厚度数据(http://nsidc.org/data/docs/daac/ae_si12_12km_tb_sea_ice_and_snow.gd.html)、来源于美国杨百翰大学(BYU)的QuikSCAT和ASCAT海冰类型数据(http://podaac-opendap.jpl.nasa.gov/opendap/allData/quikscat/preview/L3/byu_scp/sea_ice_age/arctic/v1/);用于对比验证的数据为来源于美国国家航天航空局(NASA)2011-03的北极IceBridge机载激光测高海冰厚度数据产品(http://icebridge.gsfc.nasa.gov/?page_id=732)。NASA IceBridge海冰厚度数据产品由机载平台上ATM和Snow Radar传感器获得的沿航迹(空间分辨率为40 m)高程和积雪深度协同反演得到[18]。由于航空遥感数据分辨率和精度较高,常被用作卫星遥感的验证数据。Farrell等研究表明,IceBridge海冰厚度数据的观测精度为0.05 m[18]。
通过数据内插、投影变换、空间重采样等预处理工作将上述多源数据统一为25 km空间分辨率的极方位立体投影数据集,并设定北冰洋(65°N以北)海域为本文的研究区,包括波弗特海、楚科奇海、东西伯利亚海、拉普捷夫海、喀拉海、巴伦支海、格陵兰和挪威海、巴芬湾、哈德逊湾、加拿大北极群岛海域及北极中心海域(图 1)。在参考北极海冰厚度研究相关文献 的基础上[1, 13, 16, 19],确定重点研究海域为北极中心海域、波弗特海以及格陵兰和挪威海,北极中心海域海冰通常以多年冰为主,而波弗特海海冰多以一年冰存在,格陵兰和挪威海海冰类型复杂,格陵兰岛沿岸多年冰和一年冰在该海域随着季节和年份的变化而不同。
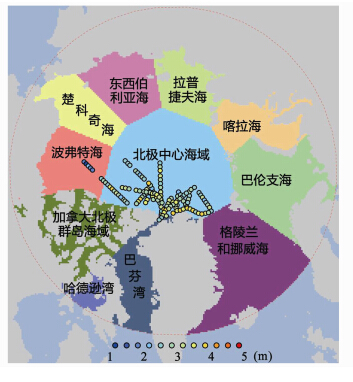
|
| 图 1 研究区及IceBridge观测的海冰厚度 Fig. 1 Study Area and IceBridge Sea Ice Thickness |
为探讨前述4种主流算法海冰厚度估算的差异性,本文基于CryoSat-2卫星测高数据,以各算法中不同的出水高度的估算方法及其模型参数取值[6, 9, 11, 13],分别估算北冰洋海冰厚度并进行比较。此外,为揭示北极不同海域不同算法及模型参数估算结果的差异情况,还对3个重点海域(北极中心海域、波弗特海、格陵兰和挪威海)分别作了掩膜处理与分析。在此基础上,通过与高精度的IceBridge海冰厚度观测数据进行空间匹配与 比较(航线上每隔25 km的所有IceBridge观测 样点平均海冰厚度值与对应位置CryoSat-2估算的海冰厚度像元值比较),以平均偏差和均方根误差最小为标准,尝试优选海冰厚度卫星测高估算的最佳算法。
不同算法的估算结果如图 2所示。就整个研究区而言,4种算法估算结果的总体空间分布较为一致,但不同算法估算的平均海冰厚度差异较大,Laxon03估算结果要比Kurtz09算法高0.476 m。4种算法估算结果的差异在一年冰区(FYI)尤为明显,达到0.713 m,这主要是由于不同估算算法中积雪厚度的数据来源不同造成的。从研究区重点海域估算结果来看(表 2),4种算法均具有格陵兰和挪威海平均海冰厚度大于波弗特海平均海冰厚度,且北极中心海域平均海冰厚度居中的特征。4种算法在波弗特海估算结果差异最大,达到0.471 m,其次是北极中心海域(0.435 m)、格陵兰和挪威海(0.402 m)。
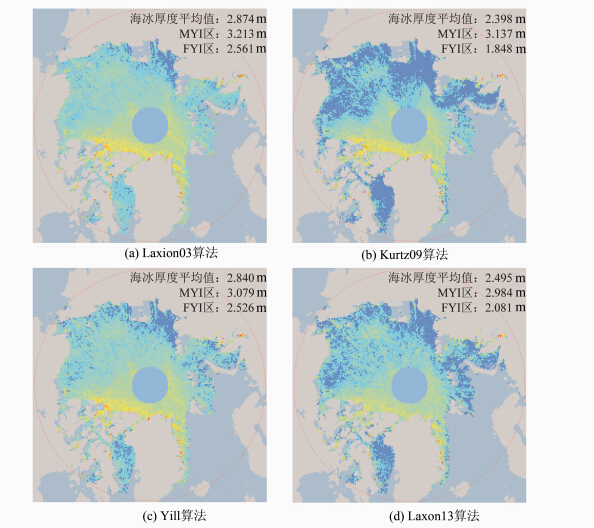
|
| 图 2 4种算法估算的海冰厚度空间分布 Fig. 2 Sea Ice Thickness Distribution Based on Four Different Algorithms |
| 算法 | 北极中心海域 | 波弗特海 | 格陵兰和挪威海 | |||
| 均值 | 标准差 | 均值 | 标准差 | 均值 | 标准差 | |
| Laxon03 | 3.403 | 0.570 | 2.853 | 0.498 | 3.318 | 0.781 |
| Kurtz09 | 3.057 | 0.564 | 2.382 | 0.510 | 2.983 | 0.814 |
| Yi11 | 3.374 | 0.576 | 2.768 | 0.504 | 3.230 | 0.791 |
| Laxon13 | 2.968 | 0.548 | 2.416 | 0.540 | 2.916 | 0.809 |
算法的比较研究表明,采用不同的算法对不同冰型、不同海域的海冰厚度估算结果产生较大的影响,因而,采用何种海冰厚度卫星测高估算算法及其模型参数更为合适,值得进一步讨论。
将前述各算法海冰厚度估算结果与IceBridge观测结果进行对比,结果如图 3所示。 对应IceBridge空间匹配后的134个观测样本,Laxon03算法的平均海冰厚度为3.131 m,Kurtz09算法的结果为3.040 m,Yi11和Laxon13算法则为3.107 m和3.057 m,4种算法的平均海冰厚度均高于IceBridge观测的海冰厚度(3.003 m),这与Farrell等研究认为IceBridge观测的海冰厚度要低估实际的海冰厚度较为一致[18]。同时,Laxon13算法估算结果与IceBridge观测结果相比较其他算法具有最小的平均偏差(0.191 m)和均方根误差(0.252 m),因而是这4种主流算法中的最优算法。算法的比较和优选研究,可为更加准确地估算和分析长时序海冰厚度变化特征提供基础和参考。

|
| 图 3 4种算法海冰厚度估算结果与IceBridge海冰厚度的比较 Fig. 3 Comparison of IceBridge and CryoSat-2 Sea Ice Thickness Based on Four Algorithms |
海冰厚度是重要的地球物理参数,利用卫星测高技术可获得大尺度长时间序列的海冰厚度信息,但由于不同学者使用算法和参数集的不同,海冰厚度卫星测高估算结果具有较大的差异性和不确定性。本文在总结前人研究的基础上,通过比较分析和对比验证方法,探讨4种常用海冰厚度卫星测高估算算法的差异,尝试确定最优的估算算法,主要结论如下。
1) 4种主流算法估算结果的空间分布较为一致,但不同算法估算的平均海冰厚度差异较大,尤其是在一年冰区;
2) 4种算法的平均海冰厚度估算结果大小依次为Laxon03算法、Yi11算法、Laxon13算法、Kurtz09算法,Laxon03算法海冰厚度估算结果较Kurtz09算法结果高0.476 m;
3) 4种算法估算的平均海冰厚度在波弗特海差异最大,达到0.471 m,其次是北极中心海域、格陵兰和挪威海;
4) Laxon13算法估算结果相对于IceBridge观测结果与其他算法相比具有最小的平均偏差和均方根误差,是卫星测高估算海冰厚度的最优算法。
本文的重点在于确定不同的海冰厚度卫星测高估算算法的差异以及现有最优的估算算法,考虑到IceBridge观测样本主要在多年冰区,未来的工作中,可进一步在北冰洋一年冰海冰区开展相关对比与验证研究,提高优选算法的普适性。
| [1] | IPCC. Climate Change 2013: the Physical Science Basis [M/OL]. http://www.ipcc.ch/report/ar5/wgl, 2013 |
| [2] | Bourke R H, Garrett R P. Sea Ice Thickness Distribution in the Arctic Ocean [J]. Cold Regions Science and Technology, 1987, 13: 259-280 |
| [3] | Hudson R. Annual Measurement of Sea-Ice Thickness Using an Upward-Looking Sonar [J]. Nature, 1990, 344(6262): 135-137 |
| [4] | Shimoda H, Endoh T, Muramoto K, et al. Observations of Sea-Ice Conditions in the Antarctic Coastal Application of Remote Sensing to the Estimation of Sea-Ice Thickness Distribution Region Using Ship-Board Video Cameras [J]. Antarctic Record, 1997, 41(1): 355-365 |
| [5] | Haas C. Evaluation of Ship-Based Electromagnetic-Inductive Thickness Measurements of Summer Sea-Ice in the Bellingshausen and Amundsen Seas Antarctica [J]. Cold Regions Science and Technology, 1998, 27: 1-16 |
| [6] | Laxon S, Peacock N, Smith D. High Interannual Variability of Sea Ice in the Arctic Region [J]. Nature, 2003, 425(6961): 947-950 |
| [7] | Kwok R, Zwally H J, Yi D. ICESat Observations of Arctic Sea Ice: A First Look [J]. Geophysical Research Letters, 2004, 31(16): L16401 |
| [8] | Kwok R, Cunningham G F. ICESat over Arctic Sea Ice: Estimation of Snow Depth and Ice Thickness [J]. Journal of Geophysical Research, 2008, 113: C08010 |
| [9] | Kurtz N T, Markus T, Cavalieri D J, et al. Estimation of Sea Ice Thickness Distributions Through the Combination of Snow Depth and Satellite Laser Altimetry Data [J]. Journal of Geophysical Research, 2009, 14(C10): C10007 |
| [10] | Kurtz N T, Markus T, Cavalieri D J, et al. Comparison of ICESat Data with Airborne Laser Altimeter Measurements over Arctic Sea-Ice[J]. IEEE Transations on Geoscience and Remote Sensing,2008,40(7):1 913-1 924 |
| [11] | Yi D, Zwally H J, Robbins J W. ICESat Observations of Seasonal and Interannual Variations of Sea-Ice Freeboard and Estimated Thickness in the Weddell Sea Antarctica (2003-2009) [J]. Annals of Glaciology, 2011, 52(9): 43-51 |
| [12] | Kurtz N T, Markus T. Satellite Observations of Antarctic Sea Ice Thickness and Volume [J]. Journal of Geophysical Research: Oceans (1978-2012), 2012, 117(C8): C08025 |
| [13] | Laxon S W, Giles K A, Ridout A L, et al. CryoSat-2 Estimates of Arctic Sea Ice Thickness and Volume [J]. Geophysical Research Letters, 2013, 40: 732-737 |
| [14] | Kern S, Khvorostovsky K, Skourup H, et al. About Uncertainties in Sea Ice Thickness Retrieval from Satellite Radar Altimetry: Results from the ESA-CCI Sea Ice ECV Project Round Robin Exercise [J]. The Cryosphere Discussions, 2014, 8(2): 1 517-1 561 |
| [15] | Ricker R, Hendricks S, Helm V, et al. Sensitivity of CryoSat-2 Arctic Sea-Ice Volume Trends on Radar-Waveform Interpretation [J]. The Cryosphere, 2014, 8(2): 1 831-1 871 |
| [16] | Kwok R. Satellite Remote Sensing of Sea-Ice Thickness and Kinematics: A Review[J]. Journal of Glaciology, 2010, 56(200): 1 129-1 140 |
| [17] | Warren S G, Rigor R G, Untersteiner N, et al. Snow Depth on Arctic Sea Ice [J]. Journal of Climate, 1999, 12(6): 1 814-1 829 |
| [18] | Farrell S L, Kurtz N, Connor L N, et al. A First Assessment of Icebridge Snow and Ice Thickness Data over Arctic Sea Ice [J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(6): 2 098-2 111 |
| [19] | Spreen G, Kern S, Stammer D, et al. Fram Strait Sea Ice Volume Export Estimated Between 2003 and 2008 from Satellite Data[J]. Geophysical Research Letters, 2009, 36(19):L19502 |
 2015, Vol. 40
2015, Vol. 40



