文章信息
- 安家春, 杜玉军, 屈小川, 杨剑
- AN Jiachun, DU Yujun, QU Xiaochuan, YANG Jian
- 掩星大气反演中的电离层二阶项效应的分析
- Analysis of Second Order Ionospheric Effects on Atmospheric Parameters Estimation in Radio Occultation
- 武汉大学学报·信息科学版, 2015, 40(11): 1440-1445
- Geomatics and Information Science of Wuhan University, 2015, 40(11): 1440-1445
- http://dx.doi.org/10.13203/j.whugis20150228
-
文章历史
- 收稿日期: 2015-04-20

2. 合肥工业大学土木与水利工程学院, 安徽 合肥, 230009;
3. 武汉理工大学土木工程与建筑学院, 湖北 武汉, 430070
2. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China;
3. School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China
利用无线电掩星反演大气参数的精度受到诸多因素的影响,主要包括卫星星历误差、钟差、地球扁率、多路径、超折射、大气水平梯度、热噪声、电离层残差等[1],在上述各种误差源中,电离层误差是最主要的误差源之一[2]。但是用于改正电离层误差的双频线性组合方法效果仍然有限。一方面是由于双频组合只能消除电离层一阶延迟项的影响,而高阶项仍然存在;另一方面,电离层的“色散”特性导致不同频率射线的传播路径并不相同,使得双频组合仍不能完全消除电离层一阶延迟项的影响。这两方面原因导致经双频改正后仍然存在电离层残余误差。在45 km以上,中性大气会完全被电离层残余误差所淹没[3]。而在太阳活动极大年,电离层残余误差的影响更加严重,43 km上的温度偏差可达1.5 K,甚至也会影响到25 km上的参数反演精度[2],限制了掩星反演结果在大气科学研究中的应用。为监测十年尺度以上的全球气候变化趋势,温度平均偏差甚至要优于0.1 K[4, 5]。因此,在无线电掩星中,为获得高精度的大气参数剖面,应尽可能地消除电离层误差的影响。文献[6]详细讨论了不同太阳活动下、不同纬度下的高阶电离层残差对掩星反演结果的影响,文献[7, 8]讨论了电离层残差对掩星变曲角和温度精度的影响。本文以三维射线追踪法为手段,重点讨论了电离层残差中的二阶项残差对反演精度的影响,以期为无线电掩星反演中的电离层误差改正方法的研究提供参考和借鉴。
1 二阶项误差定义基于掩星的大气反演中,常用的电离层改正方法是附加相应的观测值形成的无电离层组合,但仍有部分误差不能有效剔除,如式(1)所示:
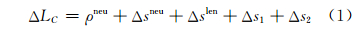
式中,Δsneu为双频组合的中性大气延迟误差项;Δslen为双频组合的附加射线长度;Δs1是不同射线路径上的TEC差异所导致的双频组合残余误差;Δs2=-(q1/f1-q2/f2)/(f12-f22)为电离层二阶项残余误差,主要是由于电离层折射指数中的地磁场项所引起的双频组合的残余误差,其中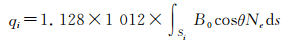 ,Si是Li的射线传播路径,B0是地磁场强度,Ne是电子密度,θ是射线传播方向与地磁场方向的夹角。Δsneu、Δslen、Δs1、Δs2都是与电离层延迟有关的误差项。其中,Δsneu、Δslen、Δs1主要是由电离层一阶项延迟所引起的,故它们的和也称为电离层一阶项残余误差[9]。本文重点关注的是Δs2,即电离层二阶项残余误差。
,Si是Li的射线传播路径,B0是地磁场强度,Ne是电子密度,θ是射线传播方向与地磁场方向的夹角。Δsneu、Δslen、Δs1、Δs2都是与电离层延迟有关的误差项。其中,Δsneu、Δslen、Δs1主要是由电离层一阶项延迟所引起的,故它们的和也称为电离层一阶项残余误差[9]。本文重点关注的是Δs2,即电离层二阶项残余误差。
在无线电掩星中,来自GNSS(globwl navigations satellite system)卫星的信号到达(Low Earth Orbit,LEO)卫星时要两次穿越电离层区域,如图 1所示,第一次为从A点至B点,称为First Ionospheric Block(FIB),第二次为从C点至LEO卫星处,称为Second Ionospheric Block(SIB)。因此,可以将式(1)中的二阶项残余误差 Δs2可写为:


|
| 图 1 无线电掩星几何关系示意图 Fig. 1 A Schematic of the GNSS/RO Geometry |
式中,Δs2FIB=-(q1FIB/f1-q2FIB/f2)/(f12-f22),Δs2SIB=-(q1SIB/f1-q2SIB/f2)/(f12-f22),Δs2FIB和Δs2SIB分别为掩星射线经过 FIB和SIB时的电离层二阶残余误差。
2 二阶项误差基本特征电离层二阶项误差与地理位置、掩星方位角关系密切,即使在同一掩星发生地和同一太阳活动水平,来自不同方位角的掩星事件的二阶项误差也有不同的值。本文仿真了6个有代表 性的掩星事件,并分析了在不同太阳活动水平下、地理位置和 地方时下的电离层二阶项误差的变化特征。
2.1 仿真方案在真实的掩星环境中,Δs2 项很难精确获得,但可通过高精度的三维射线追踪技术仿真得到。射线追踪法是基于几何光学的高频电磁波分析方法,是解决电磁波在大气中心传播问题的重要手段。在给定中性大气模型、电离层模型、地磁场模型以及GNSS/LEO掩星轨道的情况下,利用三维射线追踪技术可以模拟得到二阶项误差[10]。首先,仅采用中性大气模型来模拟信号传播;其次,采用中性大气模型、电离层模型,以及地磁场模型仿真 Li信号的传播,得到qi;将上述仿真得到的qi代入式(2),即可得到电离层二阶误差项。
本文设计了4种仿真方案(表 1),方案1仅引入中性大气模型,使用的是MSIS90模型,这是为了仿真计算仅受中性大气影响的情况;方案2、3和4中加入了电离层模型和地磁场模型,使用的分别是3D NeUoG模型和IGRF11模型,同时,为便于对比分析太阳活动强度(F10.7指数)的影响,F10.7指数分别设为70、150和220,分别表示低、中、高三种太阳活动水平。MSIS大气模型是Hedin等人[11]构建的一个全球性的三维大气模型,可计算得到中性大气密度和温度值,目前应用比较广泛的是MSIS\|90模型。NeUoG模型是由奥地利的Graz大学研发的三维电子密度经验模型[12],能够计算空间上任意点在任意时刻的电子密度值,为了保证能够用于高精度的3D射线追踪技术,该模型也能够计算空间上连续的电子密度一阶导数。国际地磁参考模型IGRF是由国际地磁与高空物理联合会建立,用于描述地球磁场中大尺度的内源场分布及其长期变化的模型,可以计算从1900年至今地球上任意点的磁场矢量,目前最新版本是IGRF\|11[13]。
| 方案编号 | 地球形状 | 中性大气模型 | 电离层模型 | 地磁场模型 | F10.7指数 |
| 方案1 | 椭球 | MSIS90 | - | - | - |
| 方案2 | 椭球 | MSIS90 | NeUoG | IGRF11 | 70 |
| 方案3 | 椭球 | MSIS90 | NeUoG | IGRF11 | 150 |
| 方案4 | 椭球 | MSIS90 | NeUoG | IGRF11 | 220 |
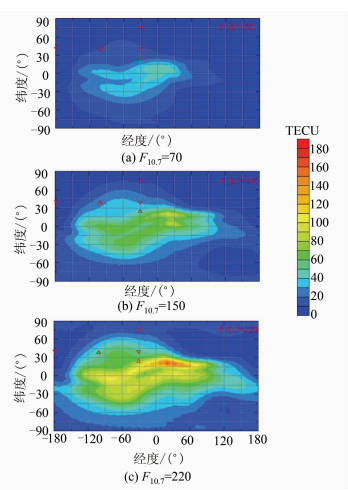
图 2给出了在3种F10.7指数下,2010年1月4日UTC 17时的全球TEC分布图。从图 2中可以看出,在赤道附近TEC具有明显的双峰结构,称为电离层赤道异常,这一异常特征随着F10.7指数的增加而更加明显。表 2给出了6次掩星事件发生地的TEC值,不同地理位置、地方时下的TEC值有所差异。在同一经线上(事件1、事件2和事件6),随着纬度的增加,TEC值变小。而在同一纬线上(事件2、事件3、事件4和事件5),地方时为15 h(事件2)的掩星发生地的TEC值较大,而地方时为5 h(事件3)的掩星发生地的TEC值较小。当F10.7为220时,全球最大TEC值约为180 TECU(1 TECU=1016 el/m3)。
|
| 图 2 2010年1月4日UTC 17h的全球TEC分布图 Fig. 2 Global TEC Map at 17h UT,on Jan. 4,2010 |
| 掩星 编号 |
纬度/ (°) |
经度/ (°) |
方位角/ (°) |
地方时/h | 事件 类型 |
TEC | ||
| F10.7=70 | F10.7=70 | F10.7=70 | ||||||
| 事件1 | 24.943 | -30.124 | 2.874 | 15 | 上升 | 16.727 | 41.344 | 72.696 |
| 事件2 | 38.532 | -30.050 | 20.346 | 15 | 下降 | 11.395 | 28.965 | 52.587 |
| 事件3 | 39.264 | -178.376 | 148.236 | 5.1 | 下降 | 2.907 | 3.447 | 3.759 |
| 事件4 | 39.119 | -100.637 | 341.599 | 10.3 | 上升 | 10.157 | 26.118 | 46.916 |
| 事件5 | 39.702 | -100.689 | 213.842 | 10.3 | 上升 | 10.035 | 25.794 | 46.33 |
| 事件6 | 74.013 | -29.273 | 136.888 | 15 | 下降 | 3.872 | 7.995 | 13.39 |
图 3给出了在不同太阳活动水平、地理位置 和地方时下的电离层二阶项误差的变化特征。随着太阳活动水平的增加,各掩星事件中的误差均相应变大。事件1、2和6位于同一子午圈,具有相同的地方时,其中事件1的电离层误差最大,而事件6的误差最小,说明低纬地区的误差要大于高纬地区,主要是由于电离层电子密度以及TEC值随着纬度的升高而不断降低。事件2~5掩星事件基本位于同一纬圈上,具有不同的地方时,分别为15 h、5.1 h、10.3 h和10.3 h,其中事件3的误差最小,表明发生于夜间或清晨的掩星事件受电离层影响较小。

|
| 图 3 6次掩星事件的电离层二阶项延迟及残余误差图 Fig. 3 Ionospheric Second Order Delay and Residual Error of 6 Occultation Events |
表 3列出了0~120 km内电离层二阶误差项绝对值的最大数值。二阶项延迟(d2ion)L1和(d2ion)L2数值很小,即使在F10.7=220时,其最大值也不过几个cm,远低于电离层一阶项延迟。如事件1的(d2ion)L1和(d2ion)L2最大值分别仅为-2.4 cm和-5.2 cm。但在中高层大气上,电离层二阶项延迟要大于中性大气延迟误差。经双频线性组合后,只是部分二阶项延迟被消除了,依然有不低于70%(Δs2占(d2ion)L1的比例)的残余误差Δs2存在。当太阳活动水平较低时(F10.7为70和150),Δs2基本在亚cm级水平,但当太阳活动水平较高时(F10.7=220),Δs2可能达到cm级,比如事件2 的Δs2最大值约为1.4 cm。而当掩星发生在中低纬度地区,且掩星方位角约为0°或180°时,Δs2也可能达到cm级,如F10.7=150时,事件1的Δs2最大值约为1.3 cm。此外,比较图 3中事件4、5的二阶项误差,不仅它们的二阶项延迟的正负号相反,而且它们的残余误差Δs2的正负号也相反。从上述分析中可知,二阶项残余误差Δs2的正负号则取决于掩星方位角以及掩星发生地的位置。
| F10.7=70 | F10.7=150 | F10.7=220 | |||||||
| (d2ion)L1/cm | (d2ion)L2/cm | Δs2/cm | (d2ion)L1 /cm | (d2ion)L2 /cm | Δs2/cm | (d2ion)L1/cm | (d2ion)L2//cm | Δs2/cm | |
| 事件1 | -1.0 | -2.1 | 0.7 | -1.8 | -3.9 | 1.3 | -2.4 | -5.2 | 1.8 |
| 事件2 | -0.5 | -1.1 | 0.4 | -1.2 | -2.5 | 0.9 | -2.0 | -4.2 | 1.4 |
| 事件3 | 0.0 | 0.1 | -0.0 | 0.1 | 0.2 | -0.1 | 0.1 | 0.3 | -0.1 |
| 事件4 | -0.5 | -1.0 | 0.3 | -1.1 | -2.3 | 0.8 | -1.8 | -3.9 | 1.3 |
| 事件5 | 0.3 | 0.7 | -0.2 | 0.8 | 1.7 | -0.6 | 1.4 | 2.9 | -1.0 |
| 事件6 | 0.0 | 0.1 | -0.0 | 0.2 | 0.4 | -0.1 | 0.4 | 0.8 | -0.3 |
结合图 3和表 3可以发现,二阶项残余误差Δs2通常在亚cm级水平,但在较高太阳活动水平下,或当掩星发生地位于中低纬度地区,且掩星方位角约为0°或180°时,可达到cm级。
3 二阶项误差全球分布特征为了更清楚地理解电离层二阶项误差Δs2与地理位置,以及掩星方位角之间的变化关系,这里进一步仿真了掩星方位角为0°时全球分布的掩星事件,并计算了相应的全球二阶项误差分布。
3.1 仿真方案本文首先仿真了一组发生于同一地点,但掩星方位角不同的掩星事件的GNSS和LEO卫星轨道。为了便于简单处理,这里所仿真的掩星事件的GNSS和LEO卫星轨道共面,且GNSS和LEO卫星均为圆轨道,其轨道高度分别为 20 000 km和800 km。地球则视为半径6 371.004 km的球体。 这些掩星事件的经纬度间隔分别为10°和5°,则共有1 332次事件。
根据所仿真的GNSS/LEO掩星轨道,并采用与§2.1同样的仿真步骤来模拟附加相位观测值和电离层二阶项延迟,仿真参数设置见表 1中的方案1和方案3。此时可以得到不受电离层影响的真正的附加相位观测值 ρneu及qiFIB和qiSIB等项。再通过式(2)即可得到FIB和SIB二阶残余误差项Δs2FIB、Δs2SIB及Δs2。
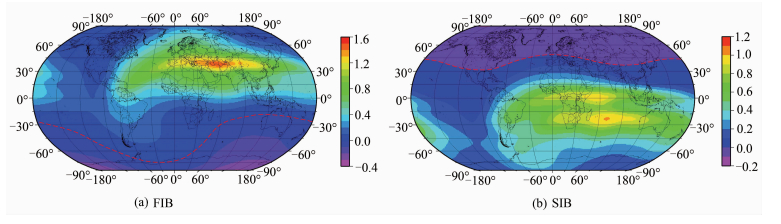
3.2 全球分布特征分析图 4给出了掩星方位角为0°时60 km上的全球FIB和SIB二阶项误差,其中红色折线表示FIB或SIB二阶项误差为零。从图中可以明显看出,当掩星方位角为0°时(即掩星射线从南向北传播),FIB二阶项误差在北半球以及南半球的大部分地区都为正值,而SIB二阶项误差则相反,在南半球以及北半球的大部分地区都为正值。正如§2.2,FIB和SIB误差的正负性与F2层峰值高度处的cosθ的正负性有关。另外,由于电离层赤道异常现象,以及周日变化特征(地方时14~16 h电子密度达到最大)的影响,FIB和SIB的二阶项误差具有明显的峰值现象,其中FIB误差具有“单峰”结构,而SIB误差具有“双峰”结构。
|
| 图 4 掩星方位角为0°时全球掩星事件60 km处FIB和SIB的二阶项误差 Fig. 4 Global FIB and SIB Error Map at 0° Azimuth and the Altitude of 60 km |
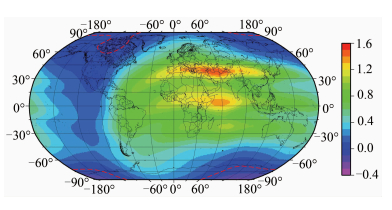
图 5为掩星方位角为0°时全球掩星事件60 km处的电离层二阶项误差Δs2分布图。当FIB和SIB具有相同正负号时,则误差会变大;而当两者符号相反时,则误差会变小。鉴于图 4中FIB和SIB二阶项误差的正负特征,除了部分高纬地区的二阶项误差Δs2为负值外(图 5中红色虚线),图 5中的全球绝大部分地区的二阶项误差Δs2都为正值。由此类推,当掩星方位角为180°时,全球绝大部分地区的二阶项误差Δs2都为负值。由于地磁场方向大致是自南向北指向的,故一般情况下全球绝大部分地区的二阶项误差Δs2的最大正值和负值约分别位于掩星方位角0°和180°,因此本文选择0°进行仿真。
|
| 图 5 掩星方位角为0°时全球掩星事件60 km处的总的二阶项残余误差 Fig. 5 Global Second Order Ionospheric Residual Error Map at 0° Azimuth and the Altitude of 60 km |
鉴于图 4中FIB误差的“单峰”结构和SIB误差的“双峰”结构,故图 5中的全球二阶项误差Δs2具有“三峰”结构特征,约分别位于30°N~45°N、0°N~15°N以及15°S~30°S之间,虽然第三个“峰”结构并不是很明显。事实上可进一步类推,在掩星方位角为0°情况下,若电离层赤道异常中的“南峰”显著大于“北峰”,那么FIB二阶项误差中将会出现“双峰”结构,而SIB误差则仅有“单峰”结构,总的电离层二阶项误差Δs2依然会具有“三峰”结构。从图 5中可以看出,在中等太阳活动水平下(F10.7=150),当掩星方位角为0°时,上述二阶项误差Δs2“三峰”结构的数值大小约在1.2~1.6 cm左右。
4 结 语本文以MSIS90大气模型、3D NeUoG电离层模型和IGRF11地磁场模型为大气背景,用三维射线追踪法模拟了无线电掩星中电离层二阶项残差的变化。结果表明,二阶项残余误差通常在亚cm级水平,但在较高太阳活动水平下,或当掩星发生地位于中低纬度地区,且掩星方位角约为0°或180°时,可达到cm级。二阶项误差在全球分布呈现出“三峰”结构,在掩星方位角为0°时三个峰值分别位于30°N~45°N、0°N~15°N以及15°S~30°S之间。因此,在掩星数据处理中,需要加强电离层监测并有效剔除电离层二阶项的干扰。另一方面,本文是用仿真手段对电离层二阶项的初步探索,主要是选取了少量有代表性的掩星事件和0°方位角时的全球掩星事件,未来的工作需要引入更准确的大气、电离层、地磁场等模型,需要选取更多掩星事件进行广泛、综合的分析,从而全面、深入地认识掩星大气反演中电离层二阶项。
| [1] | Melbourne W G, Davis E S, Duncan C B, et al. The Application of Spaceborne GPS to Atmospheric Limb Sounding and Global Change Monitoring [R]. Jet Propulsion Laboratory, California, 1994 |
| [2] | Kursinski E R, Hajj G A, Schofield J T, et al. Observing Earth's Atmosphere with Radio Occultation Measurement Use Global Positioning System [J]. Journal of Geophysical Research, 1997, 120 (D19) :23 429-23 465 |
| [3] | Hocke K. Inversion of GPS Meteorology Data [J]. Annales Geophysicae, 1997, 15 (4):443-450 |
| [4] | Steiner A K, Kirchengast G, Foelsche U, et al. GNSS Occultation Sounding for Climate Monitoring [J]. Physics and Chemistry of the Earth (Parts A), 2001, 26 (3):113-124 |
| [5] | Mannucci A J, Ao C O, Pi X, et al. The Impact of Large Scale Ionospheric Structure on Radio Occultation Retrievals [J]. Atmospheric Measurement Techniques, 2011, 4 (12):2 837-2 850 |
| [6] | Vergados P, Pagiatakis S D. Latitudinal, Solar, and Vertical Variability of Higher-Order Ionospheric Effects on Atmospheric Parameter Retrievals from Radio Occultation Measurements [J]. Journal of Geophysical Research, 2011, 116(A9), doi:10.1029/2011ja016573 |
| [7] | Liu Congliang, Kirchengast G, Zhang Kefei, et al. The Effects of Residual Ionospheric Errors on GPS Radio Occultation Temperature [J]. Chinese J Geophysics, 2014, 57(8): 2 404-2 414 (柳聪亮, Kirchengast G, Zhang Kefei, 等. 电离层残差对掩星反演温度精度的影响[J]. 地球物理学报, 2014, 57(8): 2 404-2 414) |
| [8] | Liu Congliang, Zhang Kefei, Tan Zhixiang, et al. The Effects of Ionospheric Disturbances on the Accuracy of GPS Radio Occultation Bending Angle and Temperature [J]. Geomatics and Information Science of Wuhan University, 2014, 39(11): 1 334-1 339(柳聪亮, Zhang Kefei, 谭志祥, 等. 电离层干扰对GPS掩星弯曲角和温度精度的影响[J]. 武汉大学学报·信息科学版, 2014, 39(11): 1 334-1 339) |
| [9] | Syndergaard S. On the Ionosphere Calibration in GPS Radio Occultation Measurements [J]. Radio Science, 2000, 35(3): 865-884 |
| [10] | Qu Xiaochuan. Research on Characteristics and Correction Methods of Ionospheric Error in GNSS Radio Occultation [D]. Wuhan :Wuhan University, 2014(屈小川. GNSS无线电掩星的电离层误差特性及改正方法研究[D]. 武汉:武汉大学, 2014) |
| [11] | Hedin A E. Extension of the MSIS Thermosphere Model into the Middle and Lower Atmosphere [J]. Journal of Geophysical Research, 1991, 96(A2): 1 159-1 172 |
| [12] | Leitinger R, Titheridge J E, Kirchengast G, et al. A “Simple” Global Empirical Model for the F Layer of the Ionosphere [J]. Kleinheubacher Berichte, 1996, 39: 697-704 |
| [13] | Finlay C C, Maus S, Beggan C D. International Geomagnetic Reference Field: The Eleventh Generation [J]. Geophysical Journal International, 2010, 183(3): 1 216-1 230 |
 2015, Vol. 40
2015, Vol. 40


