文章信息
- 钱海忠, 王骁, 刘海龙, 何海威, 胡慧明
- QIAN Haizhong, WANG Xiao, LIU Hailong, HE Haiwei, HU Huiming
- 利用内切圆内插等高线的算法
- A Counter Interpolation Algorithm by Using Inscribed Circle
- 武汉大学学报·信息科学版, 2015, 40(10): 1414-1420
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1414-1420
- http://dx.doi.org/10.13203/j.whugis20130806
-
文章历史
- 收稿日期: 2013-12-22

在跨尺度地图制图和表达中,地貌是最为复杂的内容之一,其中尤以等高线内插最为复杂和困难[1]。等高线内插是指在已知高程的两条等高线之间,通过内插方法自动生成与已知等高线相一致的新等高线[2]。如在利用1∶2 000地形图缩编1∶10 000地形图的过程中,等高距由2 m变为5 m,所以5 m等高线需要通过内插方法来获取。除了制图综合中的大量应用外,在等高线密集区域的地形图数字化过程中[3],也需要通过等高线内插来减少作业工作量。另外,在地图的三维地形重建过程中,通过内插加密等高线可以使重建的三维地形更加逼真。由此可见,等高线内插具有广泛的应用范围和积极的应用价值,准确、快速地内插出等高线具有十分重要的意义。
当前国内外学者对等高线内插方法进行了广泛的研究[4, 5, 6, 7, 8, 9],为解决等高线内插提供了思路和算法,从而推动了相关技术的发展。其主要方法有规则网格内插、约束三角网内插、辅助线内插等。其中文献[6]通过最小角最大原则确定相邻等高线之间的辅助线,从而内插出等高线。该方法简单易行,但当等高线形态复杂,特别是在等高线走势急剧变化且有急转弯的部位,可能会出现辅助线与原有等高线相交的情况,从而导致内插等高线与原有等高线相交。文献[7]在文献[6]的基础上进行了改进,通过在等高线上加密点,使得两条等高线的节点数相等,再利用辅助线法得到内插等高线。该方法在一定程度上能够解决文献[6]中的问题,但是数据量的增加使得内插速度难以保证。文献[8]采用基于规则格网的等高线内插方法,该方法通过建立等高线平面上的规则格网,计算格网上目标等高线高程值的位置内插出等高线。文献[9]通过构三角网来进行等高线的内插。但是,利用构网的方法内插等高线通常都比较复杂,并且内插速度较慢。
综上所述,当前等高线内插的主要问题有:
1) 当等高线走势发生急剧变化时,内插出的等高线不能很好地反映原有等高线的走势,甚至会出现内插等高线和原始等高线相交的情况。
2) 加密等高线节点使得内插得到的等高线冗余点较多,往往需进行额外的数据压缩,从而增加了运算量,并且数据压缩过程具有较强的不确定性,可能会造成内插等高线形态的变异,使得结果更为复杂。
本文结合辅助线算法,提出了一种利用内切圆进行等高线内插的方法。该方法以等高线上的节点为圆心,利用内切圆探测相邻等高线之间的空间关系,从而获得等高线间的辅助线,进而内插出等高线。该方法运算速度快,能够更为精细地反映原有等高线的走势,较好地解决了上述问题。
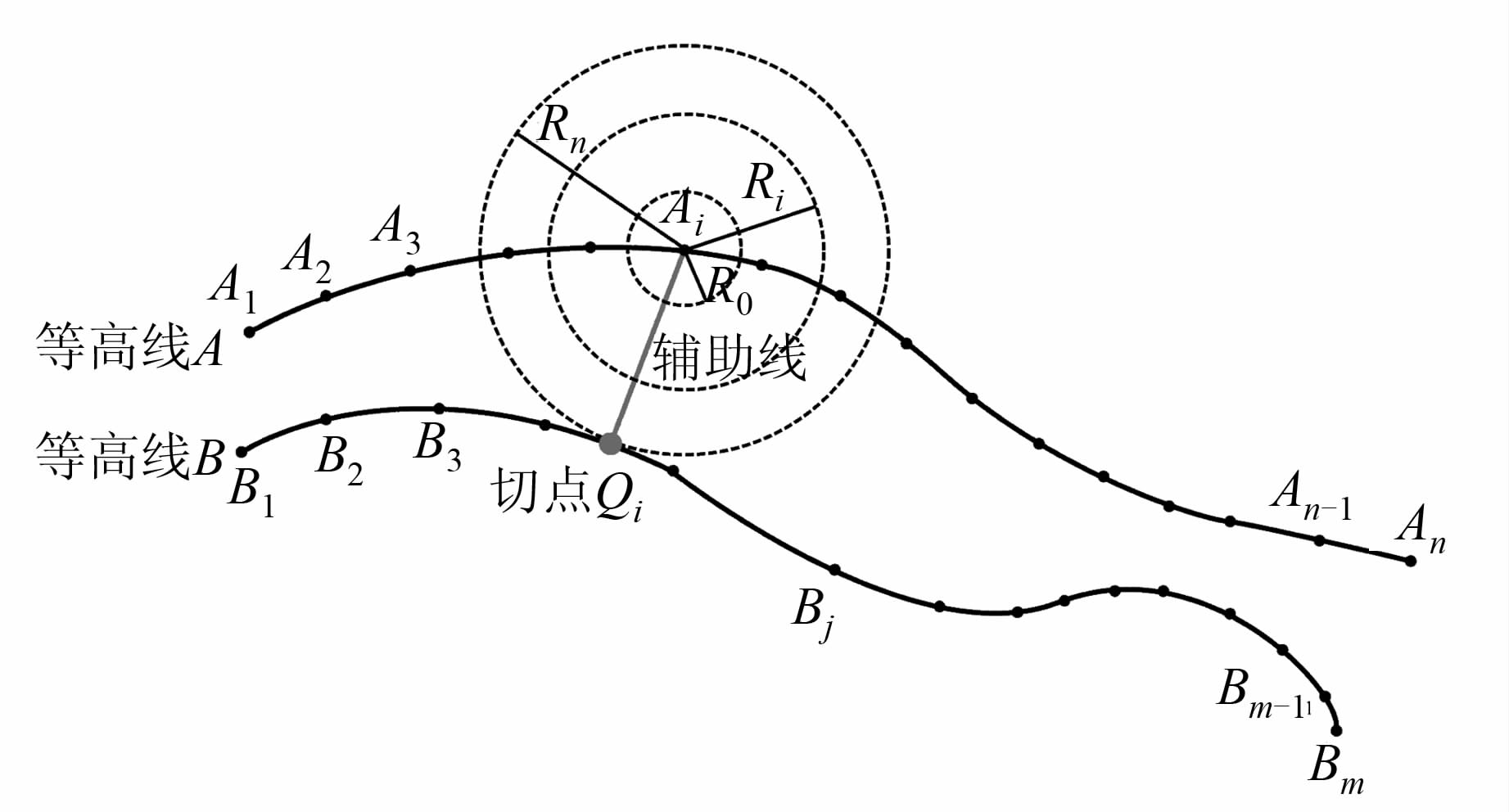
1 内切圆内插等高线算法 1.1 算法原理等高线内插的已知数据包括两条等高线各自的高程值和等高线中各节点的坐标。如图1所示,等高线 A和等高线B为原始等高线,其高程值分别为HA和HB。等高线A上的各节点为A1、A2、…、An-1、An,等高线B上的各节点为B1、B2、…、Bm-1、Bm,并且已知各节点的坐标值。
|
| 图 1 内切圆法内插等高线原理 Fig. 1 Principle of Contour Interpolation by Using Inscribed Circle |
本算法以辅助线为基础,内切圆的引入主要用于获取节点处的辅助线。该算法内插等高线的步骤如下:
1) 确定基准等高线。基准等高线是指建立的内切圆圆心所在的等高线。通常取两条等高线中节点总数较多的作为基准等高线,因为节点总数多的等高线能够更为细致地反映等高线的走势特征,保证等高线的内插效果。
2) 确定辅助线。以等高线A为基准等高线,等高线A中的节点Ai为例进行详细说明。以Ai为圆心,初始半径为R0(R0一般设置足够小)建立圆,判断该圆是否与等高线B相切,若不相切,则增大半径R0至Ri,再进行相切判断。如此循环,直至半径为Rn时,建立的圆和等高线B相切于切点Qi,连接Ai、Qi两点即为等高线A中Ai节点处的辅助线,如图1所示。据此遍历基准等高线上的所有节点,求出每个节点对应的辅助线。
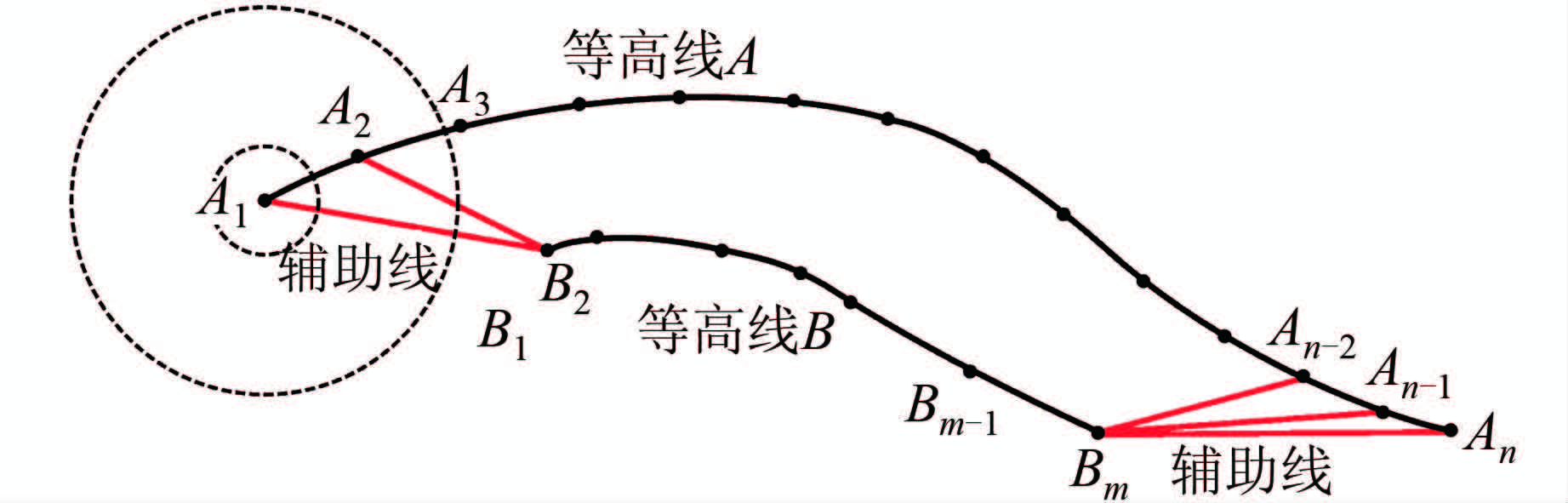
3) 确定首尾节点及其附近节点的辅助线。由于等高线的不确定性,在基准等高线的首尾节点处建立的圆可能无法和对应的相邻等高线相切。出现这种情况则直接连接该节点和对应等高线的首节点(或末节点)。如图2所示,等高线A为基准等高线,其中首节点A1及其附近的A2节点、末节点An及其附近的An-1、An-2节点无法建立与等高线B相切的圆,故直接连接这些节点和对应的首、末节点来获取其辅助线。
|
| 图 2 首尾节点及其附近节点的处理 Fig. 2 Operations of Head Node, End Node and Their Nearby Nodes |
当首尾节点构建的圆和相邻等高线相切时,仍需将首尾节点和相邻等高线对应的首节点或末节点相连,目的是保持首尾节点处等高线良好的形态特征。
4) 计算内插点坐标。在获得所有的辅助线之后,即可进行等高线的内插。设内插等高线的高程为HP,点P(XP,YP)为辅助线AiQi上的目标高程点,其中,节点Ai的坐标为(XAi,YAi),切点Qi的坐标为(XQi,YQi),m为比例系数。
其坐标计算公式为:
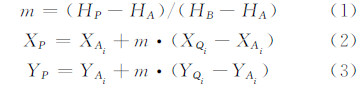
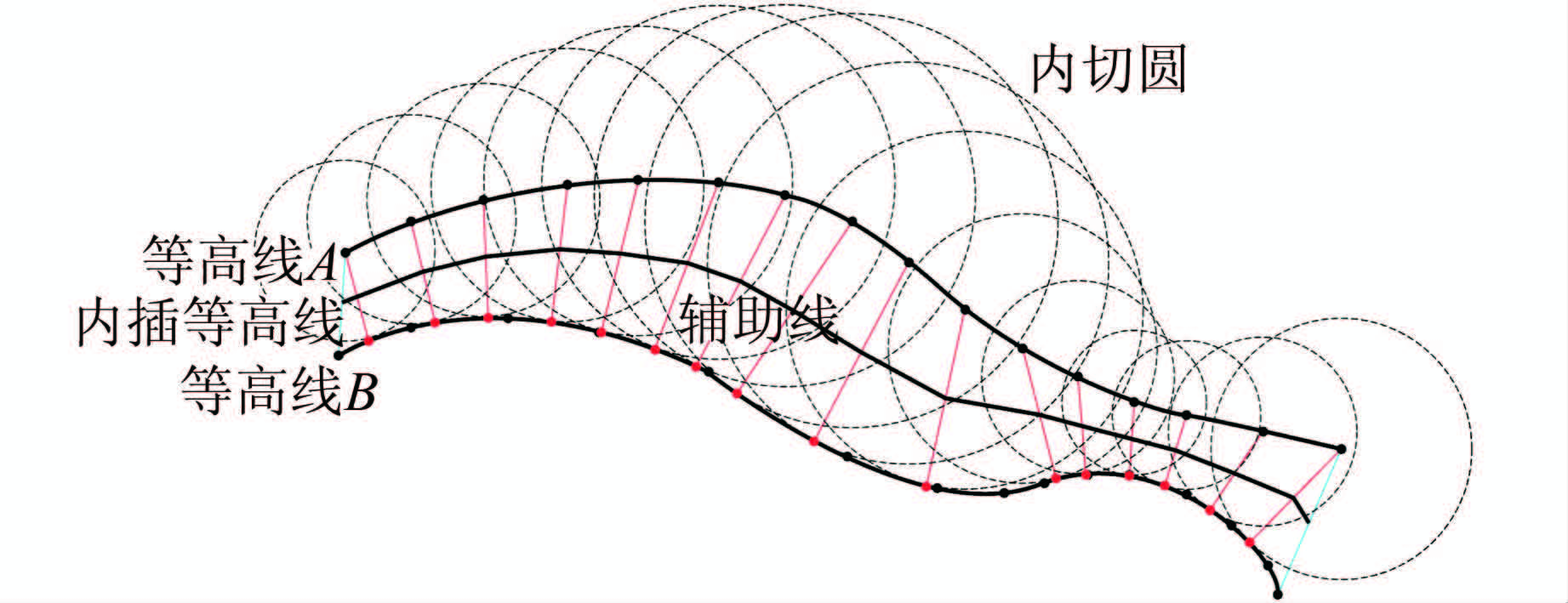
按照顺序依次连接内插点,即可得到内插等高线。图3是对一条基准等高线上所有节点建立的内切圆,并确定辅助线,进而内插等高线的效果图。
|
| 图 3 内切圆法内插等高线效果图 Fig. 3 Effect Chart Contour Interpolation by Using Inscribed Circle |
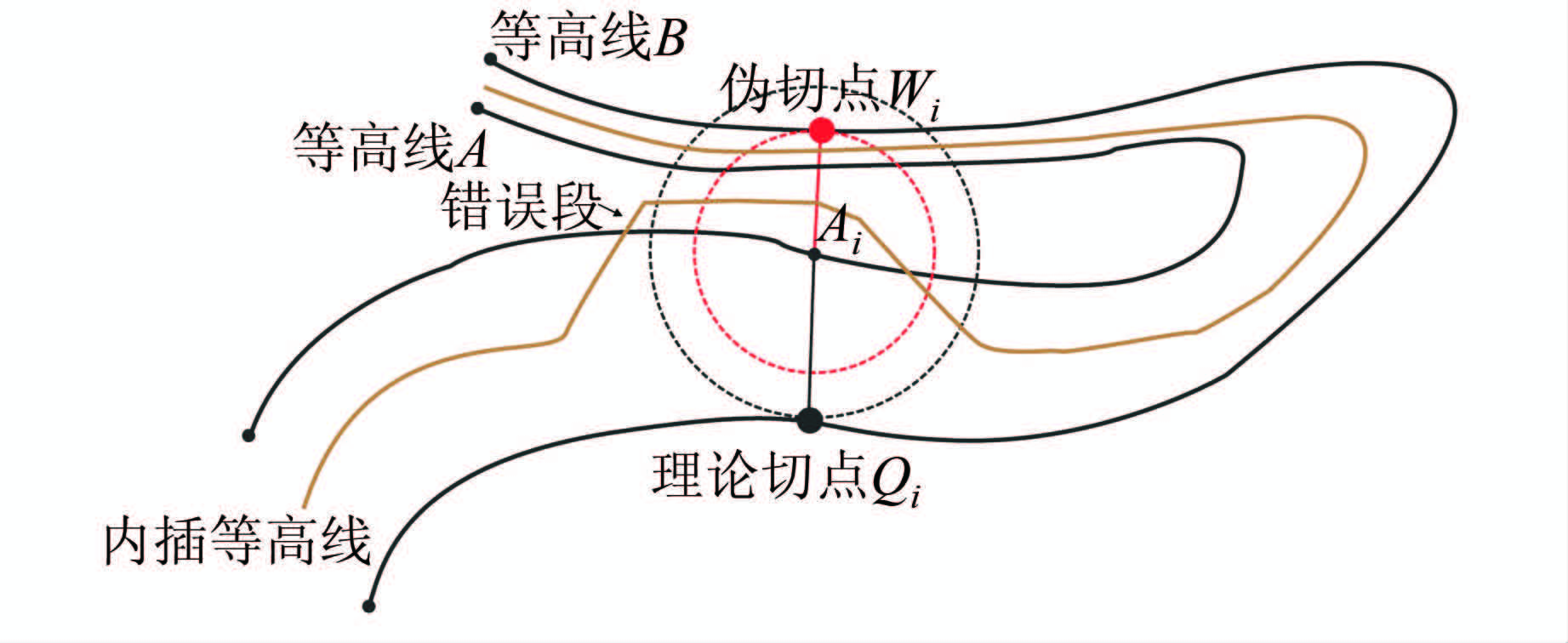
利用内切圆求内插等高线的方法存在如下问题:当等高线的走势出现急剧变化,特别是出现180°大转弯的情况时,利用内切圆法内插等高线可能会出现伪切点。如图4所示,点 Qi为等高线A中节点Ai的理论切点,点Wi为其伪切点。
|
| 图 4 伪切点的产生 Fig. 4 Pseudo Point of Tangency |
伪切点出现的原因是:求切点的过程实际上是在相邻等高线上寻找距基准等高线上的节点距离最小的点。当等高线走势发生急剧变化时,所求出的最小距离可能出现在错误的等高线段内,如图4所示,从而求出的切点不是理论切点,将其称为伪切点,继而引起内插等高线与原等高线相交的较大错误。
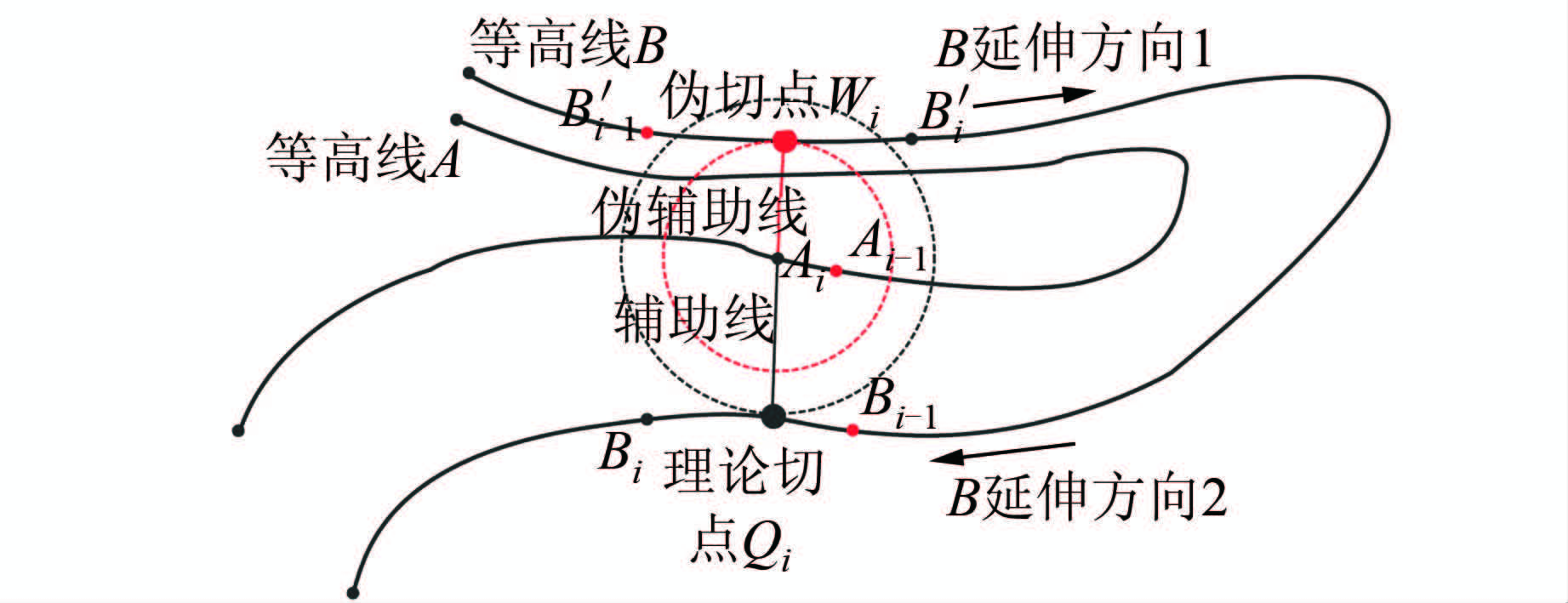
针对上述问题,采用等高线延伸方向来进行判断。在基准等高线节点上建立的内切圆,其切点应在与基准等高线延伸方向一致的相邻等高线段内[10],否则该切点为伪切点。如图5所示,由于等高线走势急剧变化,等高线B的延伸方向由1变为2,其中在等高线 A的Ai点处,等高线A的延伸方向与等高线B的延伸方向2相同,所以求出的切点应在等高线B的延伸方向2这一段内,而不是延伸方向1段内,故图5中,Wi为伪切点,而Qi为理论切点。
|
| 图 5 通过等高线延伸方向判断是否为伪切点 Fig. 5 Estimating Pseudo Point of Tangency by Contour Line Extend Direction |
判断切点真伪性的具体方法为: 取与节点Ai相邻的前一节点Ai-1,取切点所在的节点线段Bi-1Bi,判断点Ai-1、Bi-1是否在辅助线的同侧,若在同侧,则该切点为理论切点;若在异侧,则该切点为伪切点。如图5所示,理论切点Qi在线段Bi-1Bi上,Bi-1、Ai-1在辅助线的同侧;伪切点Wi在线段B′ i-1B′ i上,B′ i-1、Ai-1在辅助线的不同侧。
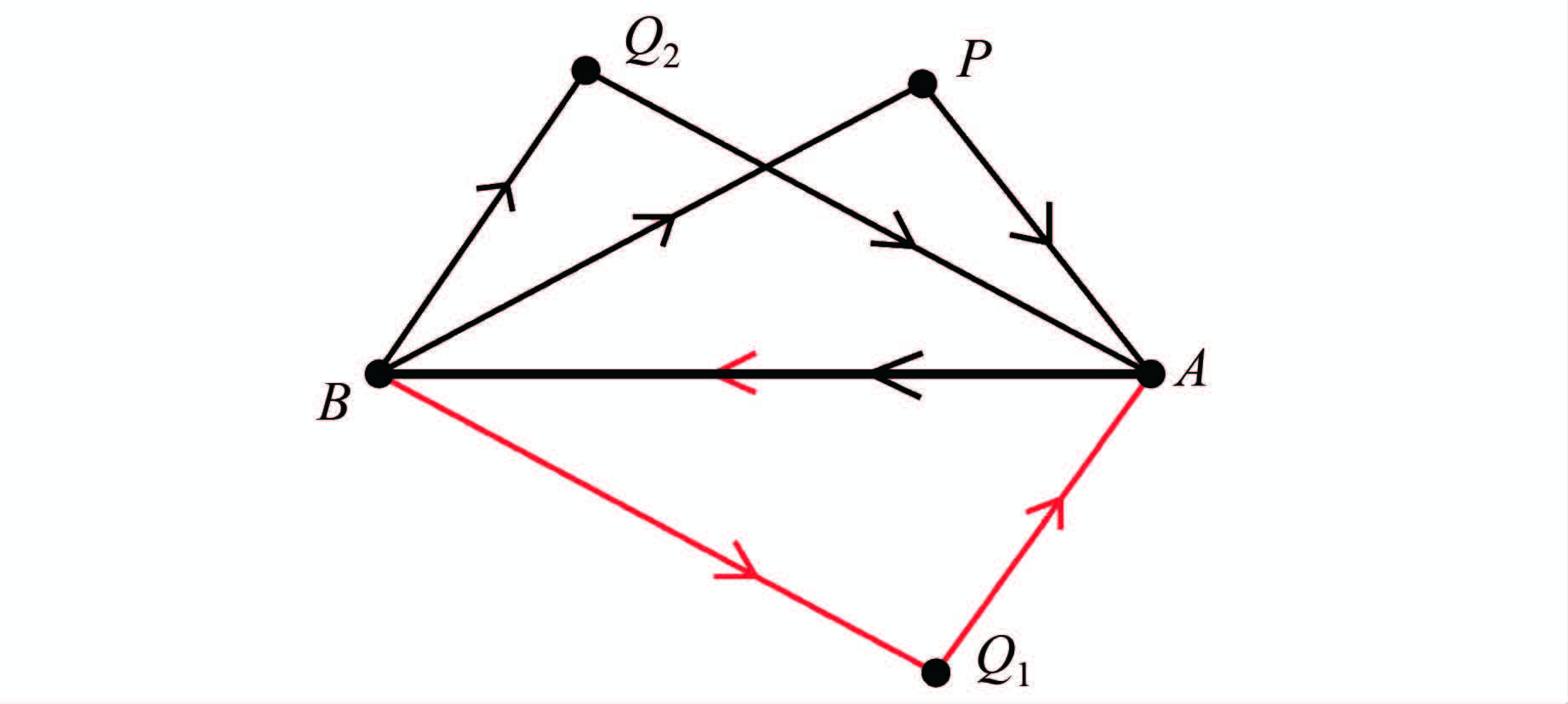
两点是否在线段的同侧可通过点和线段的时针方向进行判断。如图6所示,点P、点Q1在线段AB的异侧,点P、点Q2在线段AB的同侧。按照目标点→A→B的顺序依次连接,若两点时针方向相同,则两点在线段同侧;若两点时针方向不同,则两点在线段异侧。图6中点P、点Q1的时针方向不同,故其在线段的两侧,点P、点Q2的时针方向相同,均为顺时针,故其在线段的同侧。
|
| 图 6 利用时针方向判断两点是否在线段同侧 Fig. 6 Estimating Point in the Same Area of Line by Using Clock Direction |
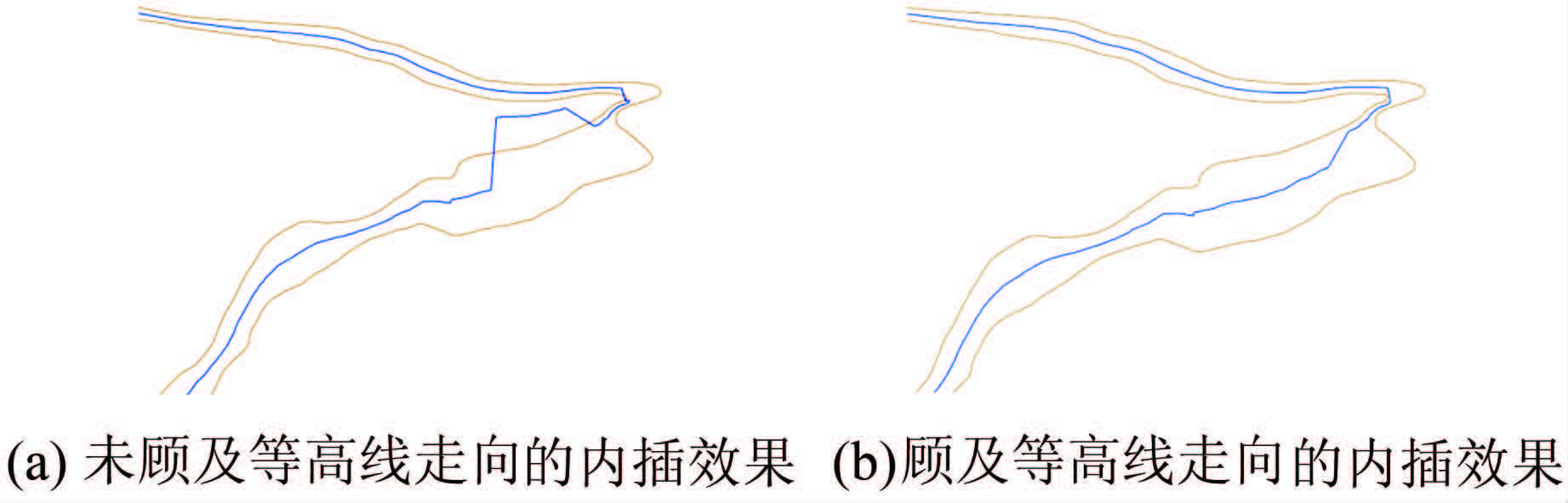
为验证上述方法对解决走势突变这一特殊问题是可行的,本文通过实验进行了验证。图7(a)为未顾及等高线走向的内插效果图,图7(b)为顾及等高线走向的内插效果图。由图7可得,在等高线走势变化巨大处,若不考虑伪切点这一情况,内插出的等高线会与原始等高线相交;相反,进行伪切点判断后,则有效避免了相交情况的发生,保证了等高线内插的质量。
|
| 图 7 等高线走向对内插效果的影响 Fig. 7 Influence on Interpolation Results by Contour Direction |
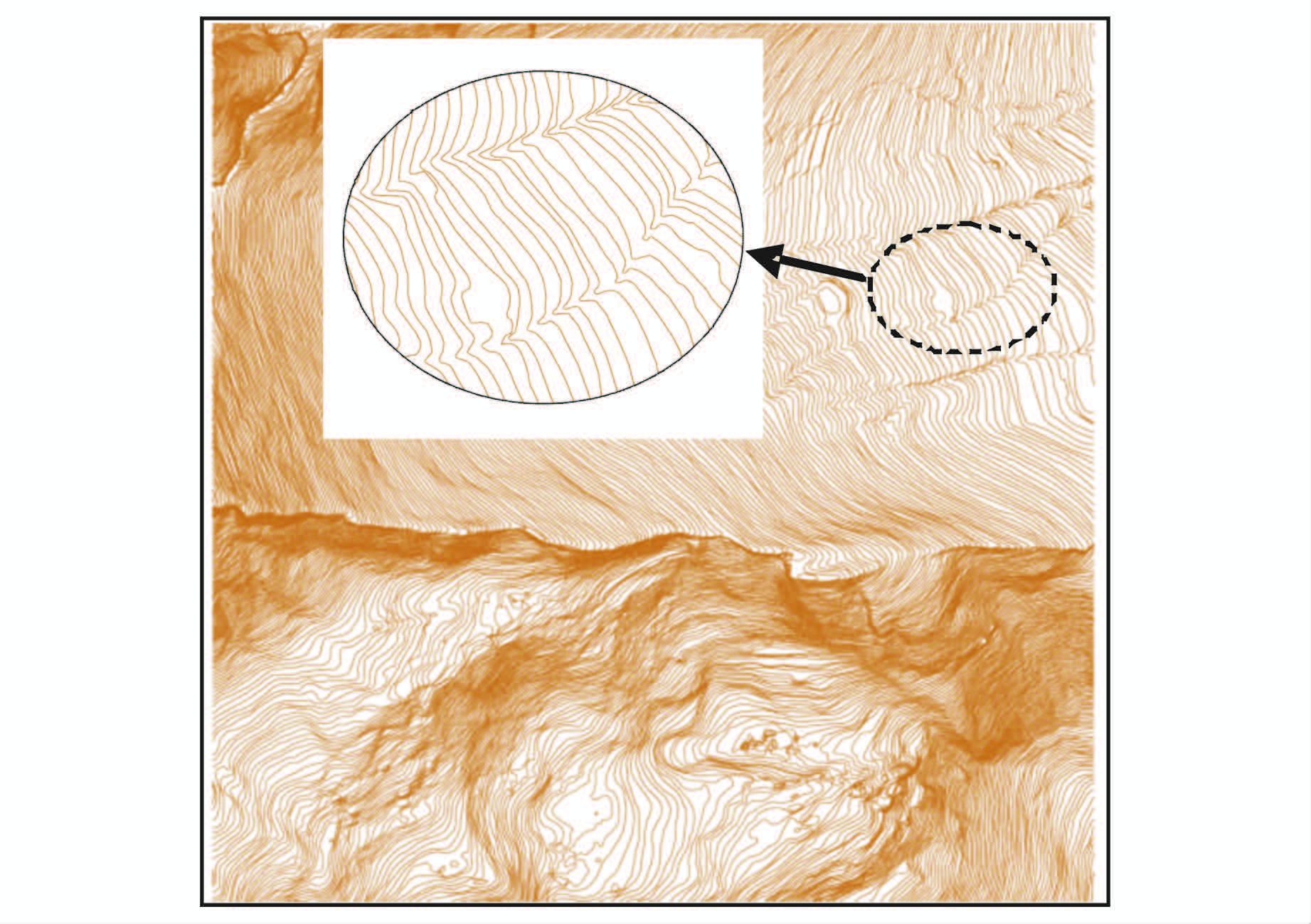
选取某区域的1∶2 000等高线数据作为数据来源,数据格式为shp格式。该格式下的等高线由一系列折线段组成,据此数据自动生成1∶10 000等高线。图8为初始1∶2 000等高线数据整体显示效果。
|
| 图 8 1∶2 000等高线初始数据 Fig. 8 1∶2 000 Contour Data |
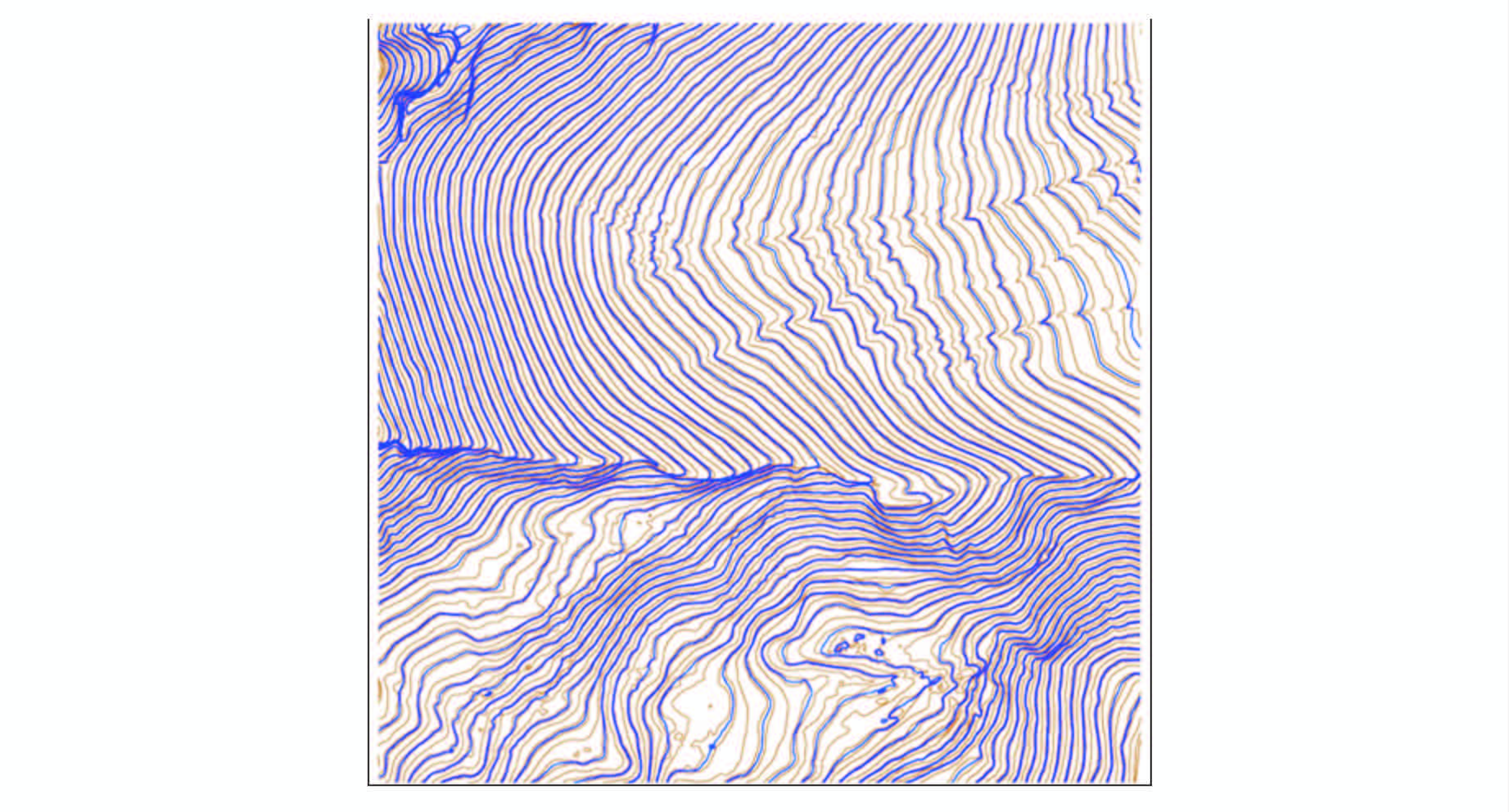
在1∶2 000地形图缩编生成1∶10 000地形图的过程中,等高距由2 m变为5 m,在进行选取之前,首先需要通过4 m、6 m等高线内插生成5 m等高线。这里为了更好地显示内插效果,将原始的4 m和6 m等高线一同进行显示。
图9、图10分别是内插效果的整体和局部放大显示,其中棕色线条表示原始等高线,蓝色线条表示内插生成的新的5 m等高线。可以看出,利用内切圆内插等高线的方法整体效果较好。
|
| 图 9 由4 m、6 m等高线内插5 m等高线效果 Fig. 9 5 m Contour Interpolation Results by 4 m,6 m Contours |

|
| 图 10 内插效果局部放大 Fig. 10 Local Magnification of Interpolation Results |
§2.2实验中,等高线内插时选择的是节点数量较多的等高线作为基准线,为验证内插基准等高线确定原则的正确性,这里选择节点数量相对较少的等高线作为基准线再次进行内插实验,图11所示为该实验的内插效果图。可以看出,在椭圆形虚线框中的区域内插效果不如§2.2的实验效果,即在成组的等高线山脊线这个明显地形特征处[11, 12, 13],以节点数较少的等高线作为基线内插出的等高线较为陡峭、平坦,弱化了山脊线的特征,而以节点数较多的等高线作为基准线内插出的等高线良好地反映了山脊线的特征。因此,以节点数较多的等高线作为基准线能够更好地保持原始等高线的弯曲特征。

|
| 图 11 以节点数较少的等高线作为基准线的内插效果 Fig. 11 Interpolation Results by Base Line with Less Nodes of Contour |
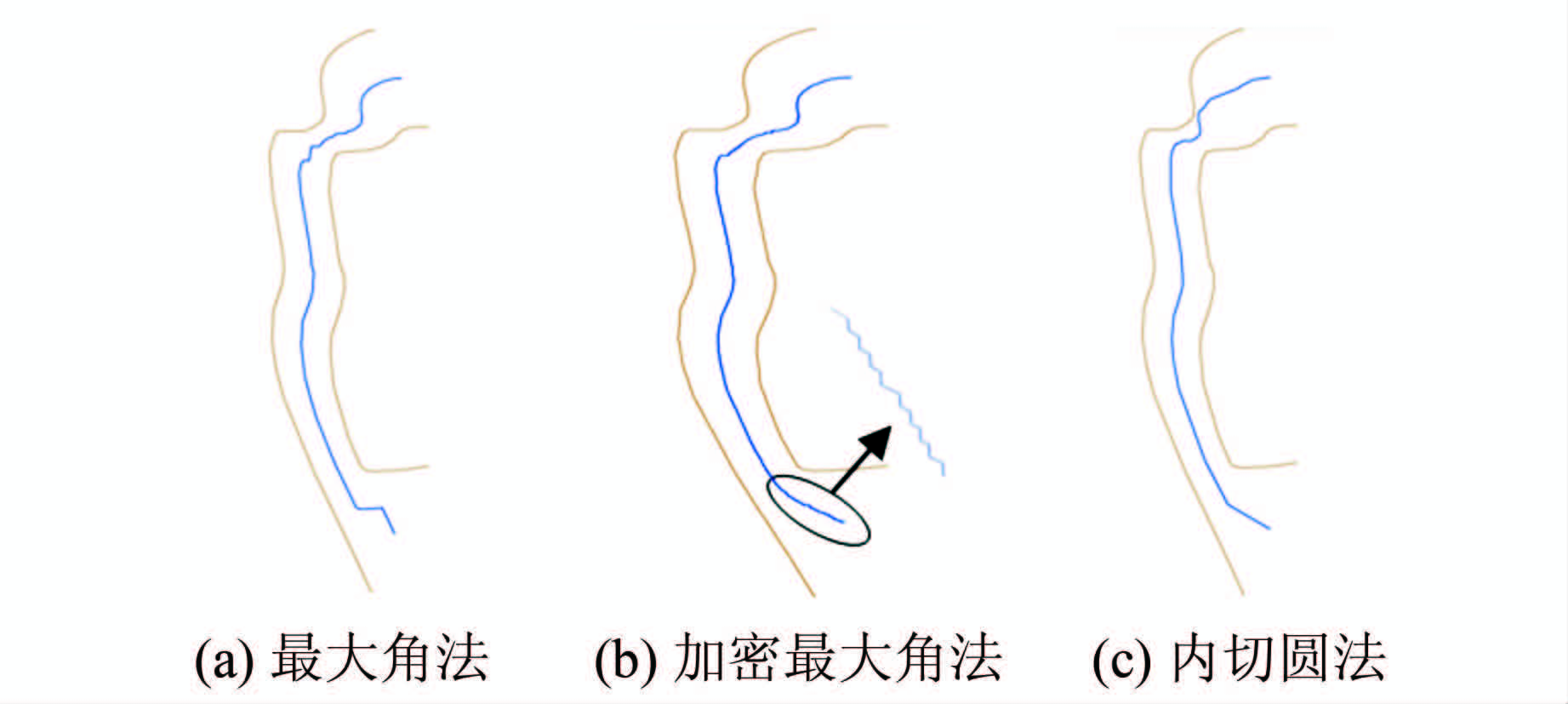
本算法的关键在于通过建立内切圆来获取辅助线,进而通过辅助线来内插等高线。通过辅助线法进行等高线内插的核心是如何寻找出最优辅助线[14],即辅助线的优劣直接关系到内插等高线的质量。当前通过辅助线内插等高线的方法主要有两种:一是文献[6]中的方法,将其称为最大角法;二是文献[7]在最大角法的基础上进行加密,将其称为加密最大角法。通过对比实验结果,从内插质量、内插时间与数据量以及内插不理想数量等3个方面对本文提出的内切圆法和其他辅助线法进行比较和分析。
3.1 内插质量比较 3.1.1 平缓等高线内插质量比较图12分别是三种方法在等高线未出现急转变化情况下的内插效果图。可以看出,内切圆法的内插效果最好,内插生成的等高线舒缓自然,未出现尖锐的角,并且能够较为精细地反映等高线的走势。相比之下,另两种方法内插得到的等高线均存在一定程度的锯齿,虽然锯齿可通过等高线化简算法[15, 16]进行消除,但显然增加了方法的复杂性,并且需要消耗更多的时间。
|
| 图 12 平缓等高线内插效果 Fig. 12 Interpolation Results of Gentle Contour |
等高线出现急剧变化的情况下,最大角法与加密最大角法的内插效果基本相同,如图13(a)所示,内切圆法的内插效果如图13(b)所示。两幅图对比可以看出,最大角法出现了较大的错误,即相交情况,并且内插等高线没有反映原始等高线在走势变化处的特征,而内切圆法内插出的等高线很好地反映了原始等高线的走势特点,效果较好。

|
| 图 13 急剧变化等高线内插效果 Fig. 13 Interpolation Results of Sharply Changed Contour |
当等高线闭合时,最大角法不能直接使用。因为最大角法通常将两条原始等高线的首节点相连作为第一条辅助线,然后再依次进行遍历。但当等高线闭合时,等高线的首尾节点相同,两条原始等高线的首尾节点可能相距很远,若仍直接相连则会出现错误。故在闭合处,首先要寻找出两条原始等高线中距离最近的两点,将其视为新的起点,并将其连线作为第一条辅助线,然后判断等高线的走向是否一致,如一致,则按照走向依次遍历;如不一致,则改变一条的走向后再依次遍历[17]。
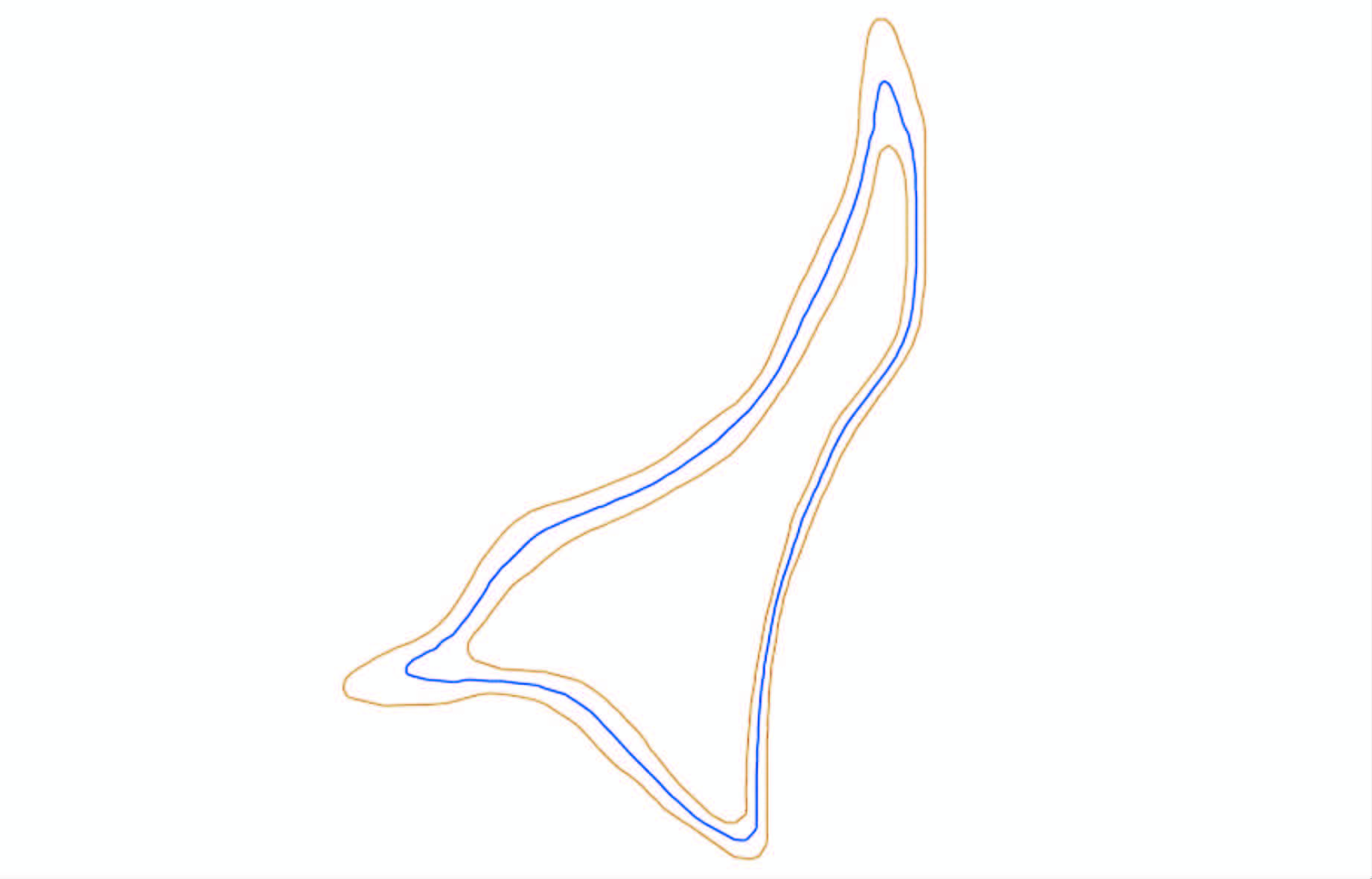
相比之下,在闭合等高线处,内切圆法不需要进行特殊的操作,只需省去连接两条原始等高线首、末节点的操作,由此可知,内切圆法内插等高线的适用范围更广。图14所示为内切圆法对闭合等高线的内插效果。
|
| 图 14 闭合等高线内插效果(内切圆法) Fig. 14 Interpolation Results of Close Contour by Using Inscribed Circle Method |
对同一地区等高线数据利用上述3种辅助线内插方法进行内插实验,并统计内插时间与内插后的数据量,得到表1中的结果。
| 方法 | 时间/s | 数据量/kB |
| 最大角法 | 5.7 | 2 243 |
| 加密最大角法 | 26.7 | 5 472 |
| 内切圆法 | 8.1 | 1 194 |
分析表1结果可得,内插时间方面,加密最大角法耗时最多,因为该算法对等高线上的节点进行了加密,因此内插时间也随之增加;内切圆法和最大角法相比时间稍长,这是因为内切圆法需要通过不断增加圆的半径来搜索切点,这一过程需要进行循环运算,从而会消耗更多的时间。
内插后的数据量方面,内切圆法的数据量最小,因为内切圆法只需对一条等高线上的所有节点遍历,所以内插后数据量较小;相反,最大角法、加密最大角法均需要对两条等高线上的所有节点进行遍历,并且加密最大角法需要加密等高线节点,因此二者内插后数据量相对较大。
3.3 内插不理想数量比较为了综合评价内切圆法与最大角法、加密最大角法的内插效果,对内插结果中不理想区域的数量进行统计,图15所示为三种方法的内插最终效果图。

|
| 图 15 不同方法内插效果 Fig. 15 Interpolation Results of Different Methods |
这里以三个指标进行衡量,分别是弯曲特征损失(包括弱化和夸大)数量、内插等高线与原始等高线相交数量、明显锯齿数量,通过人工评判得到统计结果,表2为三种方法的不理想区域的数量统计情况。
| 方法 | 相交数 | 形态损失数 | 明显锯齿数 |
| 最大角法 | 9 | 20 | 23 |
| 加密最大角法 | 8 | 15 | 26 |
| 内切圆法 | 2 | 19 | 0 |
从表2中看出,内插等高线与原始等高线相交数量方面,内切圆法明显少于另两种方法,这是因为内切圆法考虑了伪切点的情况,仍有相交现象的出现是因为数据的不确定性和复杂性;内切圆法不存在明显的锯齿情况,而最大角法、加密最大角法受自身算法的限制,均存在较多的锯齿,从而增加了后续等高线化简的复杂度;弯曲特征损失数量方面,加密最大角法最少,这与上述以节点数多的等高线作为基准线能够减少弯曲特征损失一样,由于人为对等高线节点数量进行了加密,从而能够更为细致地反映细节的形态特征,若内切圆法内插等高线前也进行节点加密处理,也能更好地保持等高线的弯曲特征,但是节点加密必然会带来效率的损失和数据量的增加,所以是否进行加密仍需视具体内插要求而定。因此根据上述的分析得出,内切圆法内插等高线的综合效果最好。
综上所述,内切圆法内插等高线的优势主要体现在以下几个方面:
1) 内插生成的新等高线能够更为精细地反映原始等高线的走势和特征。
2) 算法适用范围广泛。在等高线急剧变化处能够较好地避免内插等高线与原等高线相交的情况,在等高线闭合处,算法不需要进行调整,可直接使用。
3) 只利用一条等高线的节点信息来探测相邻等高线的走势,有效减少了数据量和计算量。
4 结 语本文分析了已有等高线内插算法,特别是辅助线算法的不足,提出一种利用内切圆内插等高线的算法。通过和其他辅助线算法的对比,该算法内插质量较高,适用范围广泛,较好地解决了当前等高线内插过程中出现的问题。实验证明了算法的科学性和有效性,从而为制图综合、地形图数字化等方面提供技术支撑。
| [1] | Wang Tao, Wu Hehai, Liu Jiping. An Algorithm for Extracting Contour Lines Based on Interval Tree from Grid DEM[J].Geomatics and Information Science of Wuhan University, 2007, 32(2): 131-134(王涛, 毋河海, 刘纪平. 基于区间树索引的等高线提取算法[J]. 武汉大学学报·信息科学版, 2007, 32(2):131-134) |
| [2] | Yang Xiaoqin. The Research of Contour Line Generating Algorithm[D]. Taiyuan: Taiyuan University of Technology, 2004(杨晓琴. 等高线生成算法的研究[D]. 太原: 太原理工大学, 2004) |
| [3] | Van Kreveld M. Efficient Methods for Isoline Extraction from a TIN[J]. International Journal of GIS, 1996, 10(5): 523-540 |
| [4] | Dupont F, Deseqhgny M P, Gonfran M. Automatic Interpretation of Contour Lines by Using External Data[C].The 4th IEEE Workshop on Applications of Computer Vision, Los Alamitos, California, 1998 |
| [5] | Chai J, Miyoshi T, Nakama E. Contour Interpolation and Surface Reconstruction of Smooth Terrain Models[C].The Visualization, Los Alamios, California, 1998 |
| [6] | Gong Youliang, He Yuhua, Fu Zi'ao, et al. A Practical Contour Interpolation Algorithm[J]. Journal of Institute of Surveying and Mapping, 2002, 19(1): 36-37(龚有亮, 何玉华, 付子傲, 等. 一种实用的等高线内插算法[J]. 测绘学院学报, 2002, 19(1):36-37) |
| [7] | Jiang Bo. A New Idea for Counter Interpolation[J]. Bulletin of Science and Technology, 2010, 26(5): 780-781(姜波. 一种等高线内插的新思路[J]. 科技通报, 2010, 26(5):780-781) |
| [8] | Su Guangjun. A Contour Tracking Algorithm Based on Regular Grid[J]. China Science and Technology Review, 2010(32):78-79 (苏广军. 基于规则格网的地图等高线快速追踪算法[J].中国科技博览, 2010(32):78-79) |
| [9] | Xu Jianxin, Xu Dibao, Duan Yuqing. A Study on the Model of Contour Interpolation[J]. Jiangsu Surveying and Mapping, 2000, 23(4): 31-33(徐建新, 徐地保, 段玉清. 等高线内插数学模型的探讨[J]. 江苏测绘, 2000, 23(4):31-33) |
| [10] | Zeng Ling. Design and Implement of Automatic Inside-insert Algorithm of Map Contour Line[J]. Shanxi Architecture, 2004, 30(18): 239-240(曾玲. 地图等高线自动内插算法的设计与实现[J]. 山西建筑, 2004, 30(18):239-240) |
| [11] | Yang Zuqiao, Li Hongsheng, Zhang Qing. Progressive Simplification Methods of Contour Line Group Constrainted by Topographic Feature[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 480-483(杨族桥, 李红省, 张青. 地形特征约束的等高线群渐进式简化方法[J]. 武汉大学学报·信息科学版, 2013, 38(4):480-483) |
| [12] | Huang Peizhi. A New Method for Extracting Terrain Feature Lines from Digitized Terrain Data[J]. Geomatics and Information Science of Wuhan University, 2001, 26(3): 247-251(黄培之. 提取山脊线和山谷线的一种新方法[J]. 武汉大学学报·信息科学版, 2001, 26(3):247-251) |
| [13] | Guo Qingsheng, Yang Zuqiao, Feng Ke. Extracting Topographic Characteristic Line from Contours[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 253-257(郭庆胜, 杨族桥, 冯科. 基于等高线提取地形特征线的研究[J]. 武汉大学学报·信息科学版, 2008, 33(3):253-257) |
| [14] | Li Hongyu, Tang Shihua, Li Jingwen, et al. An Automatic Method for Contour Interpolation Using ObjectARX Program[J]. Hydrographic Surveying and Charting, 2004, 24(3): 52-54(李洪玉, 唐诗华, 李景文, 等. 在CAD中实现等高线自动内插的一种方法[J]. 海洋测绘, 2004, 24(3):52-54) |
| [15] | Zhai Renjian, Wu Fang, Zhu Li, et al. Line Simplification Method Based on Geographic-Feature Constraint[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9): 1 021-1 025(翟仁健, 武芳, 朱丽, 等. 利用地理特征约束进行曲线化简[J]. 武汉大学学报·信息科学版, 2009, 34(9):1 021-1 025) |
| [16] | Ying Shen, Li Lin. Consistent Line Simplification Based on Constraint Points[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 488-491(应申, 李霖. 基于约束点的曲线一致性化简[J]. 武汉大学学报·信息科学版, 2003, 28(4):488-491) |
| [17] | Hu Weiming, Wu Bing, Ling Haibin. An Automatic Method for Contour Interpolation in Map Design[J]. Chinese J Computers, 2000, 23(8): 847-851(胡卫明, 吴兵, 凌海滨. 地图等高线自动内插算法[J]. 计算机学报, 2000, 23(8):847-851) |
 2015, Vol. 40
2015, Vol. 40



