文章信息
- 许炎义, 钟何平, 唐劲松
- XU Yanyi, ZHONG Heping, TANG Jinsong
- 多接收阵合成孔径声纳后向投影成像快速算法
- A Fast Back-Projection Algorithm for Multi-Receiver Synthetic Aperture Sonar
- 武汉大学学报·信息科学版, 2015, 40(10): 1409-1413
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1409-1413
- http://dx.doi.org/10.13203/j.whugis20130816
-
文章历史
- 收稿日期: 2013-12-23

水下高分辨率成像是实现水底地貌测绘、水下目标探测与搜索、水底地质鉴别与分类的基础,常用的手段有多波束声纳系统和侧扫声纳系统[1, 2]。侧扫声纳近距离分辨率高,但随着距离的增加逐渐降低,而多子阵合成孔径声纳(synthetic aperture sonar,SAS)是一种新型的高分辨率水下成像声纳,其原理是利用多个小尺寸基阵沿空间匀速直线运动来合成大孔径基阵,获得不依赖于距离和波长大小的高方位向分辨率图像[3, 4, 5]。快速高分辨率成像是SAS广泛应用的前提,多子阵SAS后向投影算法(back projection,BP)是一种精确的时域高分辨成像算法,其特点是聚焦深度高,成像空间灵活,缺点是计算量大,成为其实用化的瓶颈[6, 7, 8]。为了降低运算量,相关研究人员提出了距离多普勒算法[9]、波数域算法[10]和Chirp Scaling(CS)[11]算法,这几类算法都是对精确成像算法的近似,在一定程度上降低了成像过程中的计算量,提高了成像速度,但缺点是不易进行运动补偿。随着计算机技术的发展和信号处理能力的不断提升,对BP算法的研究又重新引起了相关科研人员的重视[12]。
为解决多子阵SAS 后向投影成像算法效率低下的问题,本文提出了一种共享内存环境下的多子阵SAS后向投影快速算法。首先根据BP算法的特点建立了动态距离徙动链表,存储不同方位距离徙动的整数和小数部分以及对应的补偿相位,节省同距离上的聚焦计算开销。然后在共享内存环境下将近距离和远距离聚焦点的计算过程相结合,以实现并行计算时的任务均衡分配,最大限度地利用计算资源。最后通过实测SAS数据的BP算法成像试验验证了所提算法的性能。
1 算法描述 1.1 SAS后向投影算法SAS后向投影算法为典型的时域算法,其思想来源于计算机层析成像,它是SAS最基本的也是最直接的成像算法。其基本原理是利用信号的相干特性,沿着某像素点对应的时域扩展函数进行相干求和,这样具备同相的回波信号得到了增强,而不同相的则实现了衰减。
对于采用线性调频机制的SAS信号,在进行BP算法成像前,首先需要进行匹配滤波和固定相位补偿。脉冲压缩后的信号在不同方位位置的徙动轨迹分布如图1所示,可以看出,同距离、不同方位的两个点目标,它们的距离徙动轨迹形状是相同的,这是设计BP快速算法的基础。
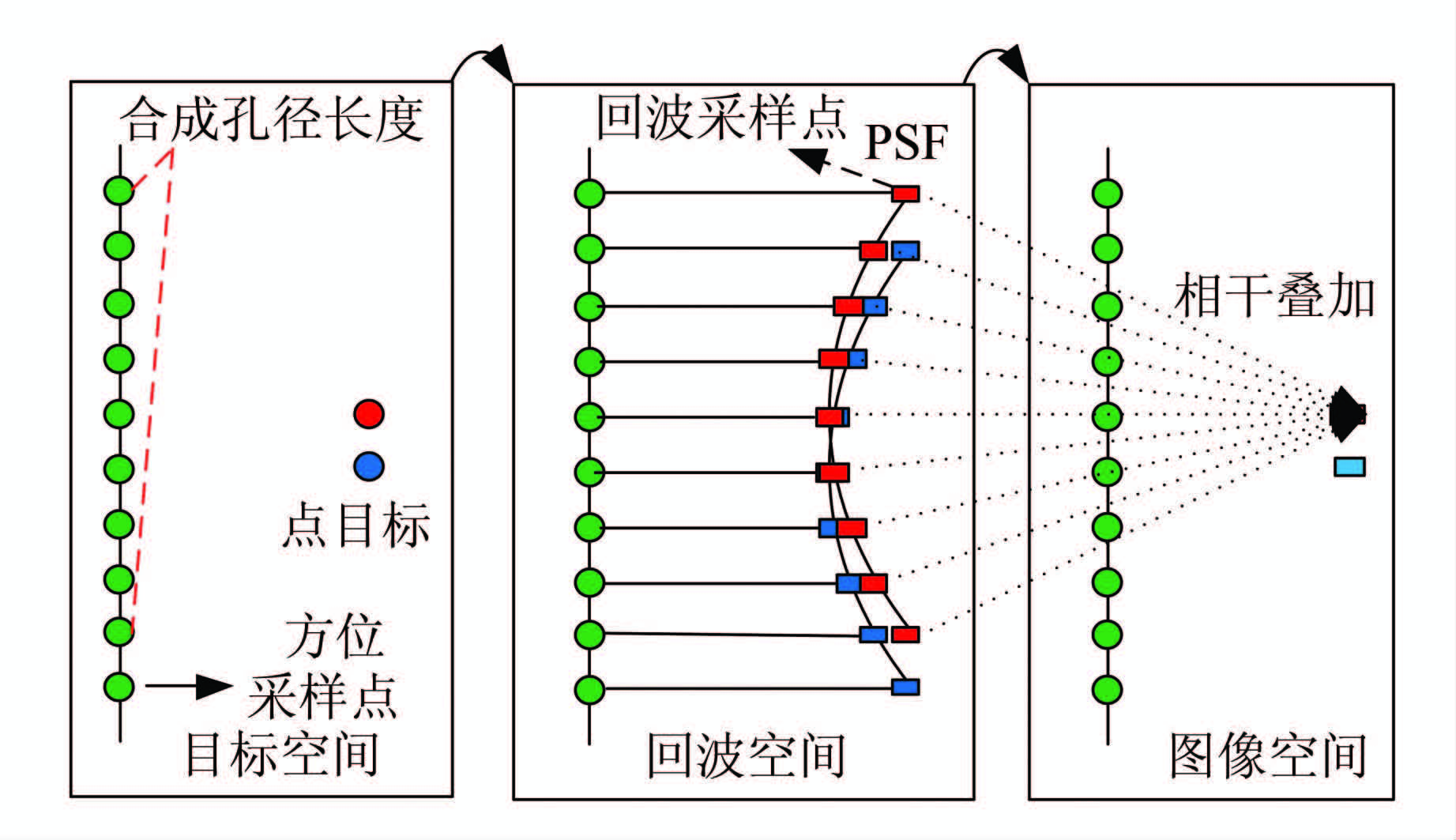
|
| 图 1 后向投影成像示意图 Fig. 1 Schematic Diagram of Back-Projection Algorithm |
假设回波场景数据的距离和方位向维数分别为Nr和Na,分辨率分别为Dr和Da。在SAS系统中,不同距离向上的合成孔径长度与到接收阵的距离关系如图2(a)所示,其中A点表示接收阵的位置。从图2中可以看出,最近距离Rmin和最远距离Rmax位置处所对应的合成孔径长度分别为L1和L2。假设脉冲压缩后,单个场景点计算延迟、插值(或取邻近值)和完成相位补偿,并进行累加的计算时间和为T0,则近距离单点聚焦时间为T0·L1/Da,远距离单点聚焦时间为T0·L2/Da,可见近距离和远距离的聚焦时间与合成孔径长度成正比。对于固定大小的场景图像,总的BP算法的成像时间为T0·Na·Nr·(L1+L2)/(2Da)。
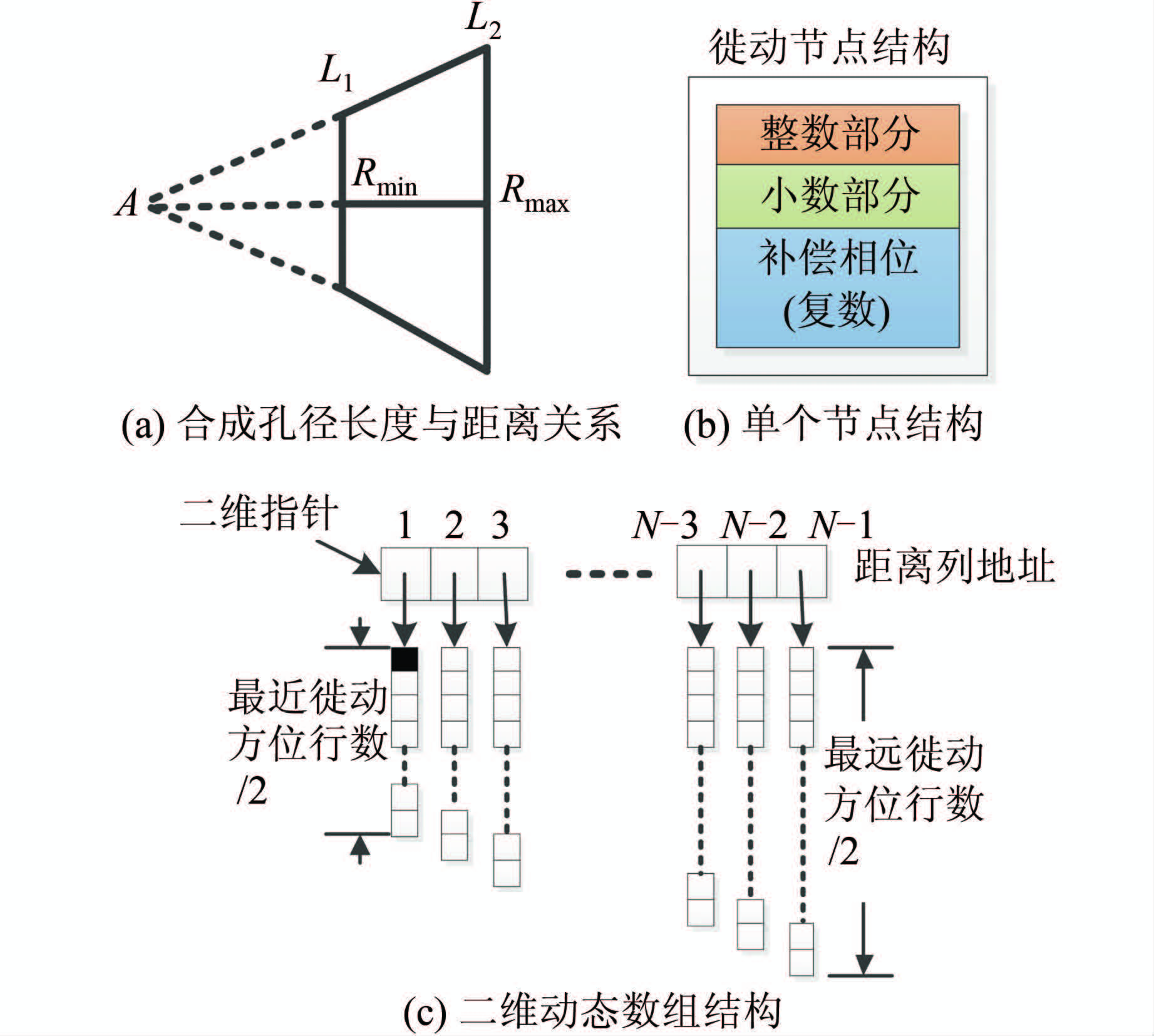
|
| 图 2 BP算法数据结构设计 Fig. 2 Data Structure Design for BP Algorithm |
为了提升算法效率,首先从单个节点的计算时间优化入手。为了避免重复计算同距离点的时延,设计了二维动态数组,用于保存同距离点、不同方位向的徙动量。设计的二维动态数组的结构如图2(c)所示,它由一个一维指针数组构成,指针数组的长度为回波数据的距离向点数Nr。每一个指针与一个距离向点相对应,该指针根据它所对应距离向位置的合成孔径长度来确定动态一维数组的大小。因为每一个点的距离徙动曲线是关于最近位置对称的,因此只需要保存一半的徙动数据,以节省内存开销。假设当前点所在位置的合成孔径长度为Li,则当前指针指向的内存空间长度只需floor(Li/(2Da)),其中floor(·)表示取整操作。
为了最大限度地节省单点聚焦时间,在动态数组图2(c)中的节点(黑色填充)里面保存了三种数据:距离徙动的整数部分、小数部分和复数形式的补偿相位,如图2(b)所示。距离徙动的整数部分和小数部分的保存主要是为了省去插值过程中的徙动量和原始数据偏移量的计算。复数形式的补偿相位是为了节省补偿时延相位的计算量。采用这种新型存储结构后,实现了将徙动量、偏移量和补偿相位计算转化为查表操作,极大地优化了BP算法的效率。
1.3 共享存储环境下的BP算法设计采用优化数据结构可以有效避免BP算法中的冗余计算,但是精确的BP成像算法的运算量由于其固有的算法复杂度,离实用还是有较大的差距。多核共享存储器计算机的出现为BP成像算法效率的提升提供了有效途径。BP算法不同聚焦点的计算过程是完全独立的,因此存在天然的并行性,难点在于计算任务的分配和数据访问冲突的避免。
OpenMP 在并行执行程序时,开始时只有一个主线程,程序中的串行区域都由主线程执行,并行部分通过派生其他线程来共同完成,并行部分结束之前是不能执行串行部分的,这就是标准的FORK-JOIN模型。基于OpenMP共享存储环境下的多子阵SAS后向投影成像算法的流程如图3所示。步骤如下:① 采用FORK-JOIN模型对原始回波数据在距离向上进行并行匹配滤波;② 采用等效相位中心近似[13]和FORK-JOIN模型对多子阵回波数据进行并行固定相位补偿,将多子阵回波数据等效为单阵收发模式;③ 采用FORK-JOIN模型对所有场景点进行聚焦,完成BP算法的并行成像,获得最终的成像结果。

|
| 图 3 多子阵SAS并行BP成像流程 Fig. 3 Flow Chart of Multi-receiver SAS Parallel BP Imaging |
由于不同方位向的匹配滤波和固定相位补偿计算量是相同的,并且处理的数据物理地址是独立的,因此步骤①和②可以直接通过parallel for指令并行处理,步骤③的并行化是BP算法并行化的难点,主要是因为对于不同距离的聚焦点,其合成孔径长度不同,导致了运算量的不同,简单任务划分将会导致计算任务的非均匀分配,降低计算资源的使用率。另外,如果采用精确算法进行计算,需要利用sinc插值,如果计算分配不当,容易产生数据冲突。
在图4中,虚线表示单个合成孔径近距离和远距离的等分线,根据几何关系,与等分线距离相等的两侧合成孔径长度和是相等的,即L1+L4=L2+L3。在进行BP成像过程中,将近距离聚焦与远距离聚焦相结合,一次循环完成与等分线距离相同的两条线上点的聚焦运算,以实现计算任务的均衡分配。

|
| 图 4 BP算法并行计算任务分配 Fig. 4 Task Allocation of Parallel Computing for BP Algorithm |
如果对徙动点采用sinc插值方法精确计算,将会涉及到同一方位相邻距离点的插值运算,在插值过程中会出现数据访问冲突。为避免数据的访问冲突,对于计算任务的分配采用静态调度策略。假设总线程数为t,让每个线程计算连续相邻的Nr/(2t)个数据列,将近距离和远距离聚焦运算结合后,总的数据列为Nr/2,这样在并行计算过程中可以有效地避免插值过程中的数据访问冲突。
2 试验结果分析为了验证所提BP快速算法的性能,进行了多子阵SAS回波数据成像试验。试验环境为:处理器为Intel(R) Xeon(R) CPU X5650 2.67 G (2处理器12核),内存48 G,显卡Tesla C2050,操作系统为Windows 7 专业版,软件环境为VS2008。试验数据选用2010年7月在某内陆湖进行干涉合成孔径声纳海试样机试验中获取的原始数据,其距离向点数为9 600点,方位向点数为3 100点,对应的幅度信息如图5(a)所示,可以看出近距离处存在水线。试验系统的基本参数如表1所示。
| 参数 | 数值 | 参数 | 数值 |
| 带宽/kHz | 40 | 脉冲间隔/ms | 200 |
| 载频/kHz | 150 | 子阵长/m | 0.08 |
| 脉宽/ms | 20 | 子阵个数 | 25 |
| 声速/ (m\5s-1) | 1 446 | 速度/(m\5s-1) | 2.5 |
| 采样率/kHz | 80 | 采样距离/m | 36~126 |
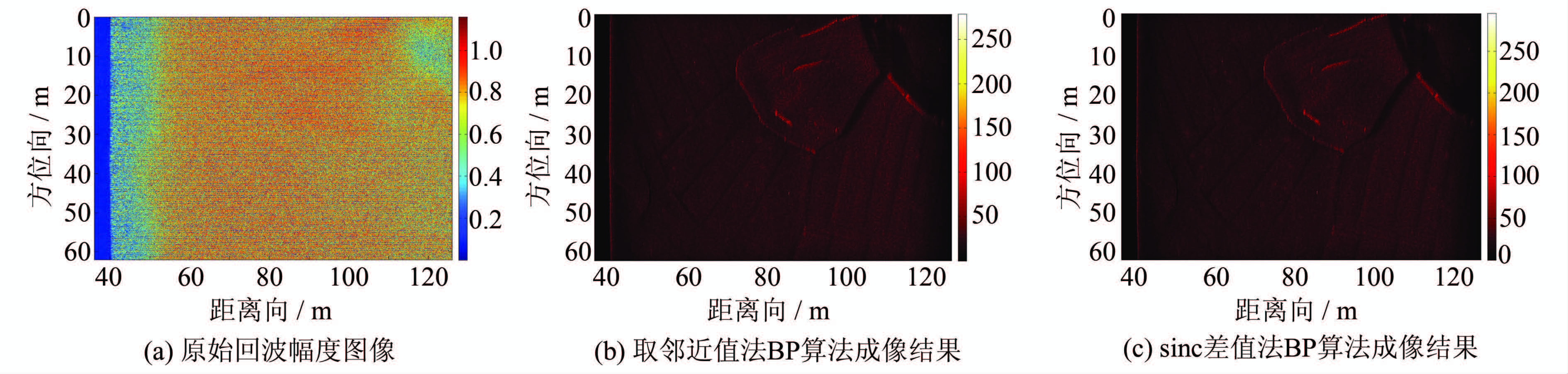
|
| 图 5 实测数据成像结果 Fig. 5 Image Results for the Real Data |
对于徙动点采用取邻近值法和sinc插值法分别进行BP成像,获得的结果如图5(b)和图5(c)所示。从对应的成像结果中可以看出,两者都非常清晰地保持了成像区域的沟壑等细节纹理信息,满足SAS高分辨成像的需求。
由于BP算法优化前后的成像结果是一致的,下面主要进行原始BP算法和改进BP算法在采用取邻近值和sinc插值两种方法下的串行和共享内存并行环境下的效率比较,结果如表2所示。表2中,每种成像方法时间中包含了方位向匹配滤波和固定相位补偿时间,这两个步骤采用的串行处理时间为9.7 s,并行处理需要1.1 s,它们在整个算法中占据的时间少。从表2中可以看出,BP算法采用取邻近插值法和sinc插值法改进前后的效率都得到了提升,但是前者从44.44 min降低到7.99 min,后者从157.9 min降低到95.28 min。采用并行后都可以得到较高的加速比,其中改进的BP算法采用sinc插值获得的加速比最高,达到11.3,改进BP算法采用取邻近值的绝对计算时间最少,为0.8 min,满足实时SAS高分辨成像的需要。
| 成像算法 | 插值方式 | 串行/min | 并行/min | 加速比 |
| 原始BP | 取邻近值 | 44.44 | 5.76 | 7.72 |
| sinc插值 | 157.9 | 26.1 | 6.05 | |
| 改进BP | 取邻近值 | 7.99 | 0.8 | 9.99 |
| sinc插值 | 95.28 | 8.46 | 11.3 |
本文提出了一种多子阵合成孔径声纳后向投影快速算法。首先根据算法的特点设计链表数据结构,保存同一距离上的徙动量,节省时延计算和相位补偿时间。然后在共享内存环境下,将远距离和近距离聚焦的计算过程相结合,实现计算任务的均衡分配,充分利用多核计算资源达到快速计算的目的。最后通过实测试验数据验证了所提算法的性能,并且取邻近值和sinc插值法都可以获得高分辨率SAS图像,但前者的成像时间远低于后者,在实际应用中,可以根据需要进行选择。
| [1] | Zhao Jianhu, Wang Aixue, Guo Jun. Study on Fusion Method of the Block Image of MBS and SSS[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 287-290(赵建虎,王爱学,郭军.多波束与侧扫声呐图像区块信息融合方法研究[J]. 武汉大学学报·信息科学版,2013, 38(3): 287-290) |
| [2] | Yang Fanlin, Wu Ziyin, Du Zhixing, et al. Co-registering and Fusion of Digital Information of Multi-beam Sonar and Side-scan Sonar [J]. Geomatics and Information Science of Wuhan University, 2006, 31(8): 740-743(阳凡林,吴自银,独知行,等.多波束声纳和侧扫声纳数字信息的配准及融合[J]. 武汉大学学报·信息科学版,2006, 31(8): 740-743) |
| [3] | Hayes M P, Gough P T. Synthetic Aperture Sonar: A Review of Current Status[J].IEEE Journal of Oceanic Engineering, 2009, 34(3):207-224 |
| [4] | Zhang Xuebo, Tang Jinsong, Zhong Heping. Chirp Scaling Imaging Algorithm for Synthetic Aperture Sonar Based on Data Fusion of Multi-receiver[J]. Journal of Harbin Engineering University, 2013, 34(2):1-6 (张学波, 唐劲松, 钟何平. 合成孔径声纳多接收阵数据融合CS成像算法[J]. 哈尔滨工程大学学报, 2013, 34(2):1-6) |
| [5] | Liu Jingnan, Yang Fanlin, Zhao Jianhu. Elementary Introduction to Synthetic Aperture Sonar and Interferometric Synthetic Aperture Sonar [J]. Hydrographic Surveying and Charting, 2003, 23(2): 1-4(刘经南,阳凡林,赵建虎. 浅析合成孔径声纳与干涉合成孔径声纳[J]. 海洋测绘, 2003, 23(2): 1-4) |
| [6] | Zhang Lei, Li Haolin, Xing Mengdao, et al. Autofocusing Synthetic Aperture Radar Imagery with Fast Back-projection Algorithm [J]. Journal of Xidian University, 2014, 41(1): 87-94(张磊,李浩林,邢孟道,等. 快速后向投影合成孔径雷达成像的自聚焦方法[J]. 西安电子科技大学学报·自然科学版, 2014, 41(1): 87-94) |
| [7] | Yegulalp A F. Fast Back-projection Algorithm for Synthetic Aperture Radar [C]. IEEE Radar Conference, Lexington,MA, 1999 |
| [8] | Ulander L M H, Hellsten H, Stenstrom G. Synthetic Aperture Radar Processing Using Fast Factorized Back-projection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 760-776 |
| [9] | Bamler R. A Comparison of Range-doppler and Wave-number Domain SAR Focusing Algorithms [J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(4): 706-713 |
| [10] | Cafforio C, Prati C, Rocca F. Full Resolution Focussing of Seasat SAR Images in the Frequency-wave Number Domain [J]. Journal of Robotic Systems, 1991, 12(3):491-510 |
| [11] | Raney R K, Runge H, Bamler R. Precision SAR Processing Without Interpolation for Range Cell Migration Correction [J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4):786-799 |
| [12] | Joshua N A. An Autofocus Method for Back-projection Imagery in Synthetic Aperture Radar[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(1): 104-108 |
| [13] | Gough P T, Hayes M P, Wilkinson D R. An Efficient Image Reconstruction Algorithm for a Multiple Hydrophone Array Synthetic Aperture Sonar [C]. ECUA 2000, Lyon, France, 2000 |
 2015, Vol. 40
2015, Vol. 40



