文章信息
- 孟伟灿, 朱述龙, 曹闻, 曹彬才, 高翔
- MENG Weican, ZHU Shulong, CAO Wen, CAO Bincai, GAO Xiang
- 线阵推扫式相机高精度在轨几何标定
- High Accuracy On-Orbit Geometric Calibration of Linear Push-broom Cameras
- 武汉大学学报·信息科学版, 2015, 40(10): 1392-1399,1413
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1392-1399,1413
- http://dx.doi.org/10.13203/j.whugis20140534
-
文章历史
- 收稿日期: 2014-07-12

2. 信息工程大学地理空间信息学院, 河南 郑州, 450052
2. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450052, China
当前线阵推扫式相机在高分辨率航天光学遥感系统中得到了广泛应用[1]。受机械振动、温度变化等因素的影响,卫星入轨后相机的几何成像参数会发生变化[2],此时如果继续使用参数的实验室标定值将无法准确描述影像的物像关系,进而影响后续影像产品的几何质量。利用高精度地面控制数据对相机几何成像参数进行在轨标定,对提高卫星影像产品的定位精度和几何质量具有重要意义。
国外在线阵推扫式相机的在轨几何标定方面开展了系统性的研究,取得了较好的成果。德国汉诺威大学采用附加参数自检校区域网平差,设置15个附加参数对印度IRS-1C卫星进行了一系列 在轨几何标定研究[3, 4];德国MOMS-2P相机在轨几何标定过程针对卫星传感器的两种立体成像模式,选择同轨长条带影像数据和交叉条带影像数据构建大骨架区域网,利用带附加参数的自检校光束法区域网平差方法实现标定参数的精化计算[5];法国空间中心采用分步标定方法,利用分布于世界各地的检校场对SPOT-5卫星进行静态参数(传感器内部参数、传感器相对位置关系等外部参数)标定和动态参数(轨道和姿态参数)标定,实现了SPOT-5卫星影像的高精度定位[6, 7, 8];美国IKONOS卫星通过设置视场角映射、光学畸变 参数、焦平面阵列的布置以及相机安置矩阵等参数,实现了对相机几何技术参数的精化,最终在无控制点条件下达到平面12 m(RMS)、高程10 m(RMS)的定位精度[9, 10, 11];日本ALOS/PRISM相机的在轨几何标定工作利用多个检校场设置30个附加参数探测系统误差,取得了较好的效果[12, 13]。
国内学者对星载线阵推扫式光学相机的在轨几何标定也进行了诸多研究。王任享提出了等效框幅像片(equivalent frame photo,EFP)光束法空中三角测量方法,并利用模拟的三线阵卫星影像进行了一系列标定试验[14];李晶等对天绘一号三线阵立体测绘相机的主点、主距、相机夹角、相机安置矩阵等参数进行了在轨标定,实验结果表明可有效地消除系统误差[15];徐建艳和祝小勇等分别利用广义偏置矩阵来校正外部误差源综合引起的成像偏差,可显著提高影像的定位精度[16, 17];袁修孝等分别研究了基于常差和系统误差的姿态角改正模型,对相机姿态角系统误差进行了标定,利用少量控制点可显著提高影像的定位精度[18, 19];雷蓉分析了星载线阵推扫式相机的内方位自检校参数模型和外方位元素模型,以此为基础建立了自检校光束法区域网平差模型,利用模拟数据和PRISM实际数据进行了自检校区域网平差实验[20];王涛首先利用姿态角常差对外参数进行标定,然后采用自检校区域网平差技术和资源三号真实数据实现了传感器内、外参数的整体求解[21];郝雪涛等采用三阶畸变模型描述线阵推扫式相机的内部畸变,并基于CCD探元间的角度不变原理对参数进行解算,利用HJ-1A/1B卫星数据进行了实验,检校误差残留在2~6个像元[22];杨博等采用安置矩阵和三阶指向角模型对资源一号02C卫星全色相机进行了在轨几何标定,标定后影像的定位精度显著提高,且内标定精度优于0.3像元[23];王密等以资源三号卫星三线阵相机和资源一号02C卫星全色相机为例,针对具体相机设计提出了相应的在轨几何标定方案,标定后影像的无控和有控几何定位精度显著提升,且由于影像内部畸变的消除,利用更少量的控制点即可达到高于标定前的定位精度[24];蒋永华等利用偏置矩阵和物理内参数模型对资源三号三线阵影像进行了高精度几何检校,取得了良好的效果[25]。
本文分析了线阵推扫式相机的物理内参数模型与指向角内参数模型的区别与联系,对物理模型到指向角模型的演化过程进行了推导,分析了偏视场相机与正视场相机在使用指向角模型时的不同,并分别给出了两者的具体计算公式。在严格几何模型中引入偏置矩阵外标定模型和指向角内标定模型,得到了线阵推扫式相机的在轨几何标定模型。采用先外后内、分步求解的策略进行参数解算,并利用嵩山检校场高精度控制数据和天绘一号高分影像对标定模型和求解方法进行了实验验证。
1 线阵推扫式相机的在轨几何标定模型 1.1 严格几何模型严格几何模型是在轨几何标定的基础,根据线阵推扫式相机的成像几何构建严格几何模型[26],如式(1)所示:
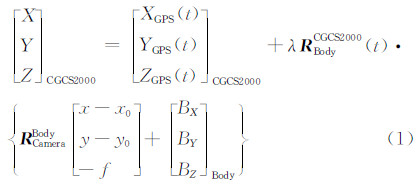
式中,CGCS2000表示国家2000坐标系;(X,Y,Z)CGCS2000为地面点在CGCS2000坐标系中的坐标;(XGPS(t),YGPS(t),ZGPS(t))为t时刻星载GPS天线相位中心的位置;λ为比例因子; R BodyCGCS2000(t)为t时刻卫星本体坐标系到 CGCS2000坐标系的旋转矩阵; RCamera Body为相机坐标系到卫星本体坐标系的旋转矩阵;(x0,y0,f)为主点、主距;(BX,BY,BZ)Body代表相机投影中心与GPS天线相位中心在卫星本体坐标系中的偏移量。
1.2 在轨几何标定模型式(1)能最为准确地描述线阵推扫式相机的成像几何,但其参数众多,且参数间具有强相关性,因此其并不适宜直接作为在轨几何标定模型。本文在该严格几何模型的基础上,通过对参数进行综合取舍和模型简化,构建了线阵推扫式相机的在轨几何标定模型。
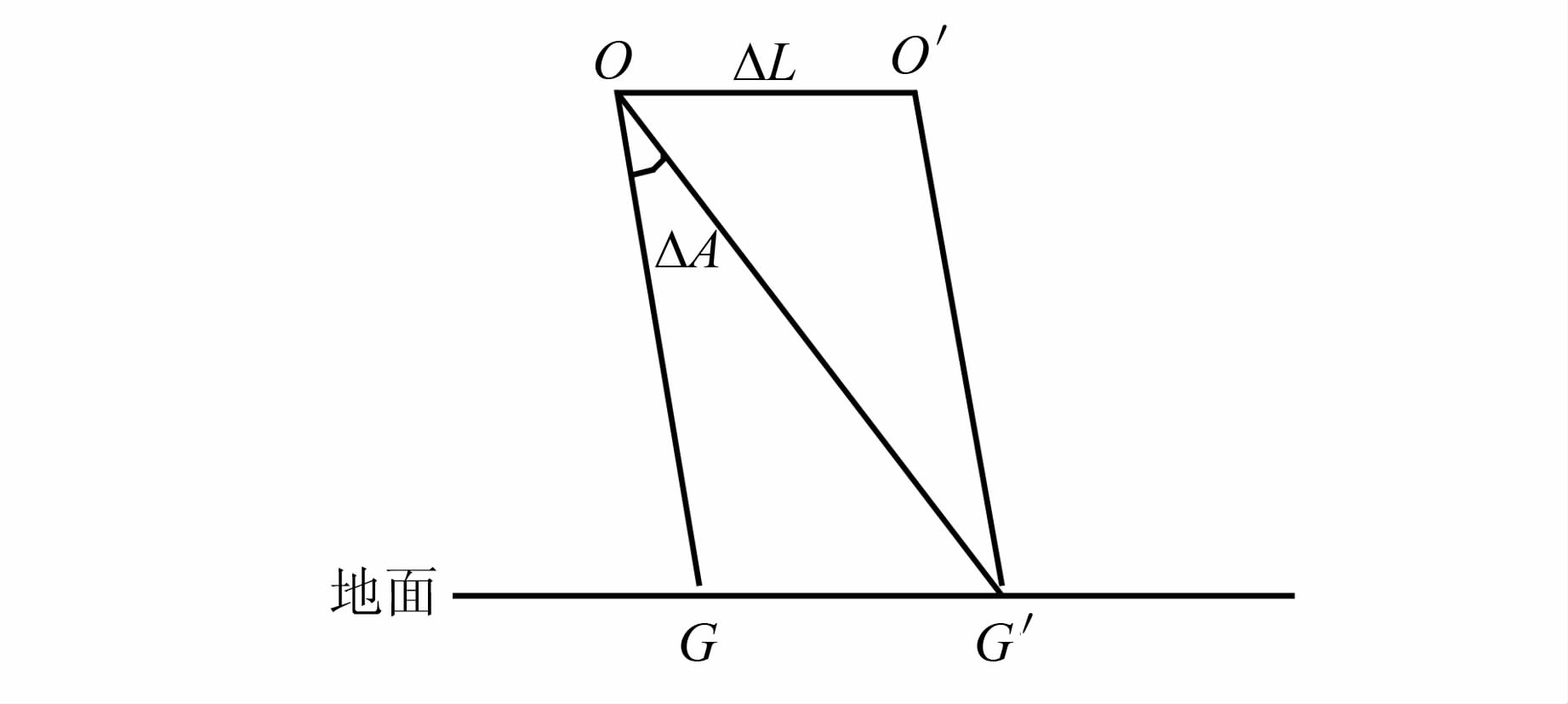
1.2.1 基于偏置矩阵的外标定模型线阵推扫式相机的外部系统误差主要包括卫星定轨误差、卫星测姿误差、时间测量误差、相机投影中心与星载GPS天线相位中心的偏心误差、相机在卫星上的安置误差。在上述误差项中,卫星定轨误差和GPS偏心误差均属于线元素误差,而卫星测姿误差和相机安置误差均属于角元素误差,对于时间测量误差,其可等效为沿轨方向的线元素误差。如图1所示,线元素误差与角元素误差对最终几何定位的影响可根据一定的关系进行等效处理[27]。图1中,O为相机成像时的实际位置,O′为测量出的位置,线元素误差为ΔL。
由图1中几何关系可发现,线元素误差ΔL所引起的几何定位偏差GG′可完全等效为角元素误差ΔA所引起的,即线元素误差和角元素误差具有等效性。据此引入广义偏置矩阵 R U来消除姿、轨测量误差、GPS偏心差、相机安置误差以及时间测量误差等外部误差。引入偏置矩阵后的几何模型如式(2)所示,由于 R U已经包含了GPS偏心差的影响,因此式(3)中不再包含GPS偏心差项。

式中 ,φ、ω、κ为Y-X-Z转角系统的3个旋转角。为描述3个旋转角随时间累积的漂移误差,利用式(4)进行拓展[28]。

式中,t表示当前行的成像时刻;t0表示本景影像起始行的成像时刻。
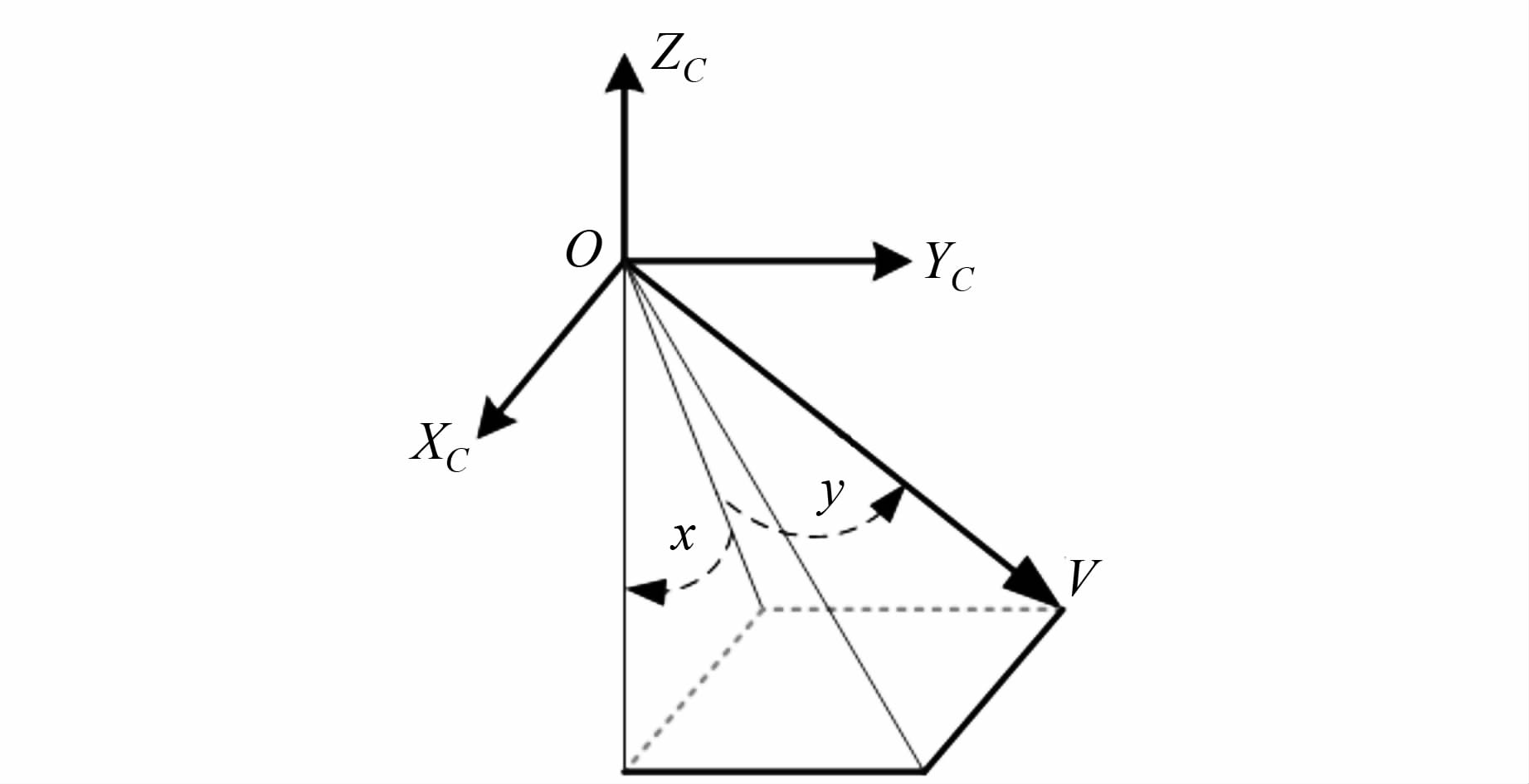
1.2.2 基于探元指向角的内标定模型指向角(φx,φy)是相机内方位元素的集成,其可确定某探元s在相机坐标系下的光线指向。指向角示意图如图2所示,其中O-XCYCZC为相机坐标系。
1) 物理模型到指向角模型的推导
传统上,一般采用物理模型描述相机的内部畸变,该模型中的各项参数均有明确的物理含义。 对于线阵推扫式相机而言,一般考虑主点偏移、光学畸变、CCD平移、旋转、缩放等因素,如式(5)所示:

式中,(Δx0,Δy0)表示主点偏移和CCD平移;k1和k2为镜头径向畸变系数;p1和p2为镜头偏心畸变系数;sy为CCD尺度变化因子;θ为CCD线阵旋转角;( x,y)=(x-x0,y-y0);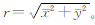 。
。
虽然物理畸变模型的各项参数均具备明确的物理意义,但由于内外参数间的相关性以及内参数间的相关性,各物理参数均难以被准确计算出来。例如,垂轨方向的CCD平移误差 Δy0与相机角元素误差ω之间存在相关性,无论是虚拟观测值法或是分步解算法等,都不能将两者准确地计算出来,因此,Δy0的标定值与真实值之间会存在一定的偏差。同理,对于物理畸变模型的其他参数,该种情况也普遍存在。物理畸变模型的物理性和严密性仅存在于理论层面,但并不适用于实际计算。
虽然各物理畸变参数的真实值无法被准确标定出来,但在经过基于偏置矩阵的外标定所确定的广义相机坐标系下,各探元的指向(φx,φy)是可以准确确定的,该指向实际上是各物理畸变参数综合作用的结果。下面对物理模型到指向角模型的过程进行推导,分析偏视场相机与正视场相机在使用指向角模型时的不同,并分别给出了两者的具体计算公式。
不考虑相机畸变的指向角计算公式为:
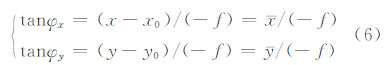
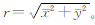 代入式(7),展开、合并关于y的同类项可得式(8)。其中,y为探元编号s的线性函数,式(8)即为指向角畸变模型的初步公式。
代入式(7),展开、合并关于y的同类项可得式(8)。其中,y为探元编号s的线性函数,式(8)即为指向角畸变模型的初步公式。
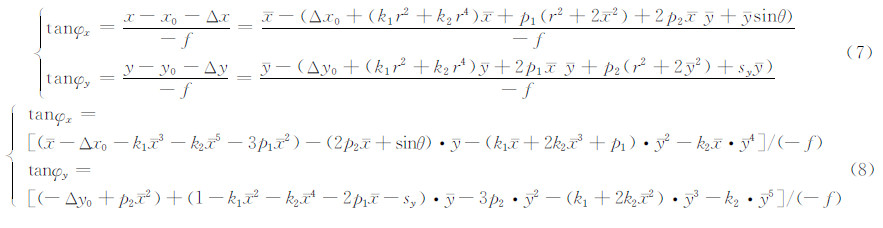
2) 正视场相机和偏视场相机指向角畸变模型的不同
根据焦平面上CCD摆放位置的不同,线阵CCD相机可分为正视场相机和偏视场相机两种。如图3所示,正视场相机的CCD摆放在视场中央,主点位于CCD线阵上;偏视场相机的CCD摆放在视场一侧,即主点位于CCD线阵一侧。

|
| 图 3 正视场焦面和偏视场焦面 Fig. 3 Field Central Focal Plane and Field Bias Focal Plane |
对于正视场线阵CCD相机,x≈0,式(8)可简化为:
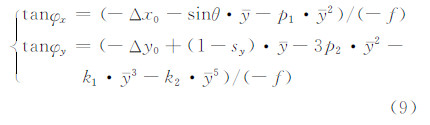
由式(9)可导出正视场线阵CCD相机的指向角畸变模型为:
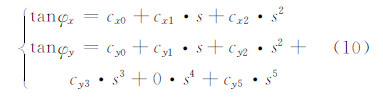
对于偏视场线阵CCD相机,x为不等于零的常数,y为探元编号s的线性函数,则可由式(8)导出偏视场线阵CCD相机的指向角畸变模型:
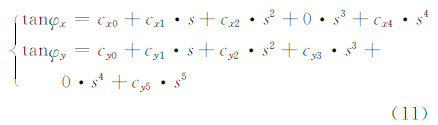
式(10)和式(11)即为正视场相机和偏视场相机的指向角畸变模型,前者为后者的一种特例。
综合外标定模型和内标定模型,可得到线阵推扫式相机的在轨标定模型为:
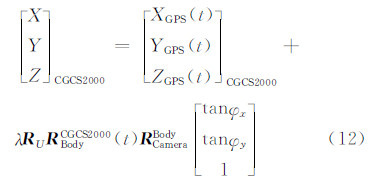
待求解的参数包括内、外标定参数两类,由星载线阵推扫相机的成像原理可知,外标定参数是动态变化的,而内标定参数是相对稳定的。采用先外后内的求解方法,首先对外标定参数进行求解,此时外部误差及内部误差中的线性部分将会得到补偿,内部误差非线性的部分将会被残留;然后对内标定参数进行求解,将残留的非线性误差进一步补偿。该求解方法与文中标定模型相结合,可计算出稳定的内参数。通过最终标定出的内参数和外参数,可准确还原物方空间坐标系中的光线指向。
用 ParaE和 Para I分别表示需标定的外参数和内参数,则有:
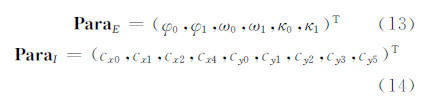
参数解算步骤如下:
1) 在影像上选取N个沿线阵方向均匀分布的地面控制点,其中,第j个点的CGCS2000空间直角坐标为(Xj,Yj,Zj),对应的影像坐标为(Linej,Samplej),j=1,2,…,N;
2) 令式(12)中的 R U R BodyCGCS2000(t) R CameraBody=  ,则式(12)可转化为:
,则式(12)可转化为:
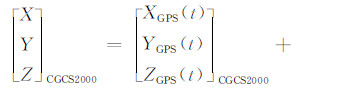
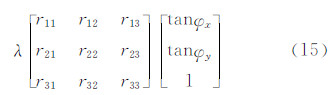
转换为物方到像方的方程,消除λ,得:
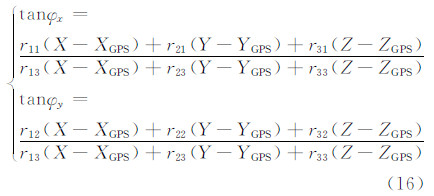
3) 对 Para E和 Para I分别赋初始值,Para E赋值为0,Para I根据相机物理内参数的实验室标定值进行计算;
4) 将内参数 Para I视为真值,对式(17)进行线性化,建立误差方程,并求解外参数 Para E;
5)将求解出的 Para E视为真值,对内标定参数 Para I进行求解,求解步骤与4)相似;
6) 循环执行步骤4)和5),当两类参数的值趋于稳定时,停止计算。
3 实验与分析为验证本文标定模型和求解方法的有效性和可靠性,共设计了三组实验:①内参数在轨标定值与实验室标定值比较实验;②内参数两次在轨标定一致性检验实验;③内参数在轨标定前后定位精度对比实验。
实验数据包括两景同一地区(嵩山)、成像时间间隔22 d的天绘一号高分影像,图像大小为35 000像素×4 096像素,传感器为TH-1-01高分相机,编号分别为135-1和135-2,成像时间分别为2010-11-28和2010-12-20,影像空间分辨率为2 m,含云量均低于2%。
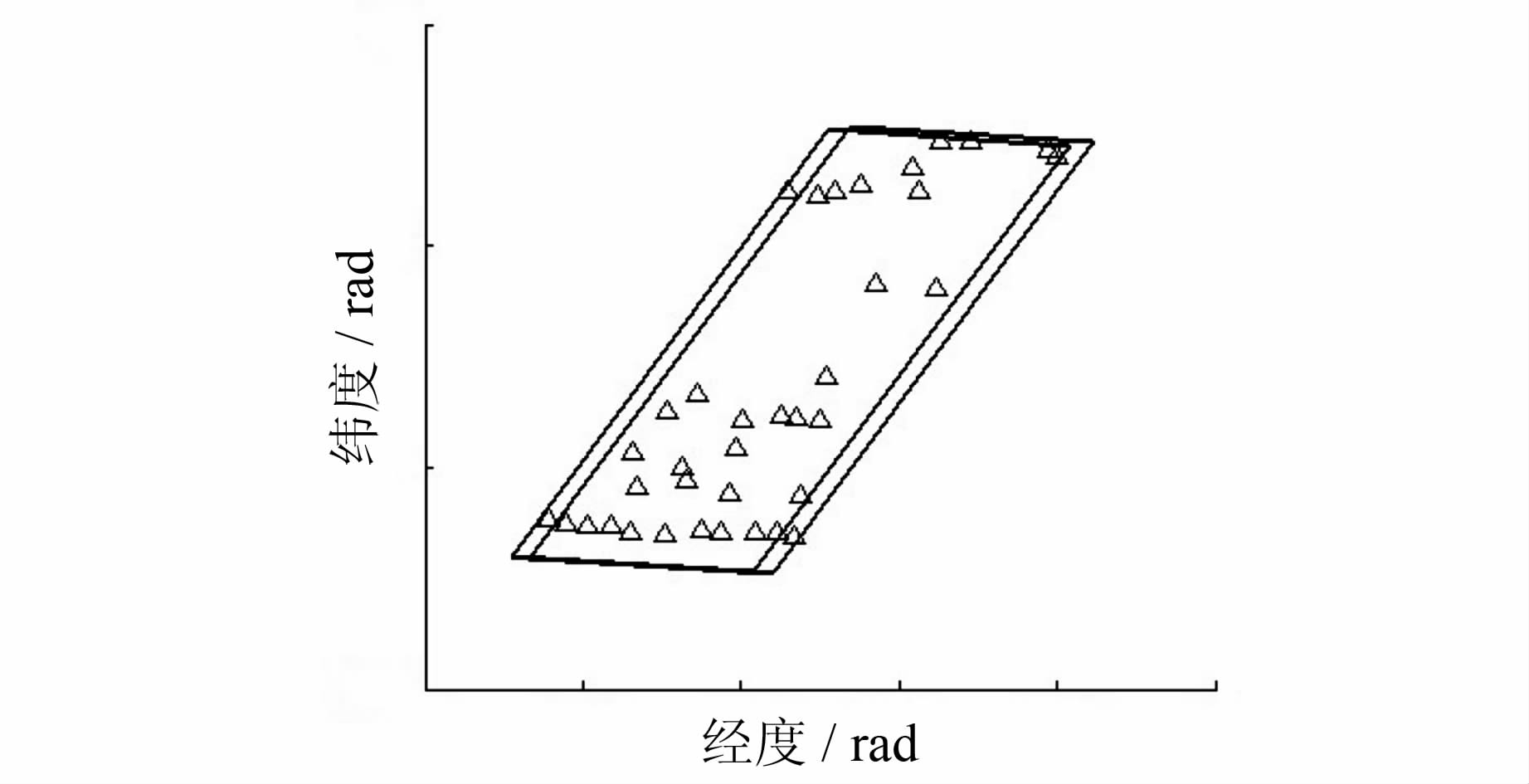
野外实测dm级GPS控制点37个,像点坐标由3名作业员人工量测取均值,精度优于1像素。两景影像的覆盖范围及控制点分布见图4。
|
| 图 4 影像地面覆盖范围及控制点分布 Fig. 4 Image Coverage Range and GCPs’ Distribution |
根据内参数在轨标定值和实验室标定值计算在轨标定前后CCD探元指向的差异,一定程度上可反映相机内部的畸变程度。
实验步骤如下:
1) 采用135-1影像,选取沿线阵方向分布均匀、沿飞行方向分布集中的10个控制点,按照本文方法对相机进行在轨标定;
2) 每隔50个探元选取一个样本,计算样本探元在轨标定前后沿轨方向和垂轨方向的指向差异(乘以焦距的理论值将该差异转化为像元);
3) 根据差异绘制畸变曲线如图5所示,畸变统计结果见表1。
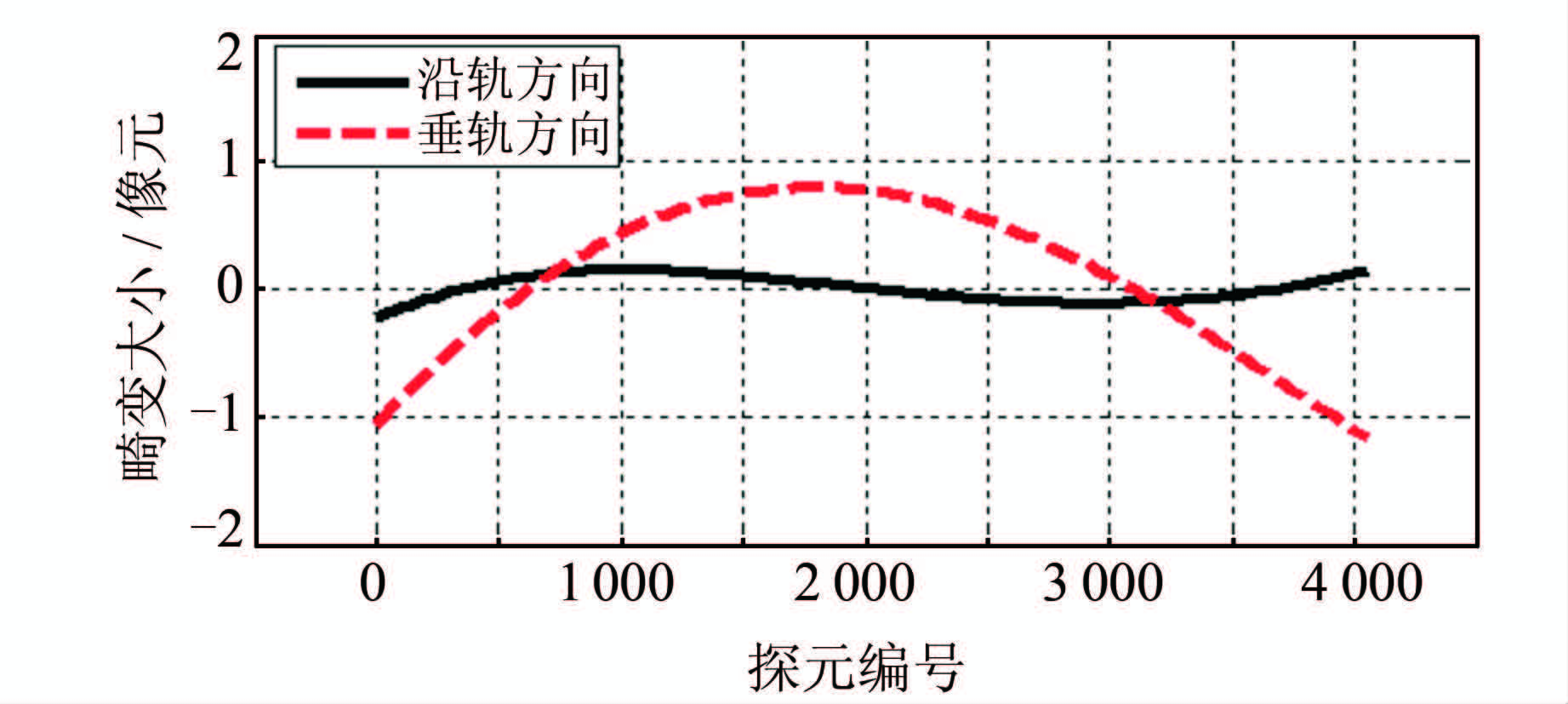
|
| 图 5 135-1标定出的CCD畸变曲线 Fig. 5 CCD Distortion Curve Calibrated by Data 135-1 |
| 统计项目 | 数值 | |
| 最大 | 0.234 6 | |
| 沿轨方向畸变 | 最小 | 0.000 5 |
| 均方根 | 0.098 2 | |
| 最大 | 1.180 4 | |
| 垂轨方向畸变 | 最小 | 0.003 1 |
| 均方根 | 0.610 3 |
分析图5和表1可发现,垂轨方向的最大畸变为1.18像元,沿轨方向的最大畸变为0.23像元。
3.2 内参数两次在轨标定一致性检验实验为验证本文算法的稳定性,采用135-2数据对相机进行第二次在轨标定。将135-2和135-1两次标定得到的内参数结果进行比较,若两次标定结果具备一致性,则可证明本文标定方法的稳定性,同时可从侧面反映本文标定结果的正确性。
实验步骤如下:
1) 采用135-2影像,按照本文方法对线阵CCD相机进行第二次在轨标定;
2) 根据135-2在轨标定结果绘制畸变曲线,如图6所示;

|
| 图 6 135-2标定出的CCD畸变曲线 Fig. 6 CCD Distortion Curve Calibrated by Data 135-2 |
3) 每隔50个探元选取一个样本,统计样本探元两次在轨标定的指向差异(乘以焦距的理论值将该差异转化为像元),如表2所示。
| 差异区间/像元 | 沿轨方向差异统计 | 垂轨方向差异统计 | ||
| 样本个数 | 百分比/% | 样本个数 | 百分比/% | |
| 0.0~0.1 | 78 | 95.12 | 58 | 70.73 |
| 0.1~0.2 | 4 | 4.88 | 18 | 21.95 |
| 0.2~0.3 | 0 | 0.00 | 6 | 7.32 |
| 0.3~0.4 | 0 | 0.00 | 0 | 0.00 |
| 0.4~0.5 | 0 | 0.00 | 0 | 0.00 |
| 中误差/像元 | 0.026 2 | 0.065 3 | ||
| 注:总样本数为82。 | ||||
对比图6和图5可发现,两次标定得到的相机畸变曲线稳健一致。由表2统计数据可发现,95.12%的样本探元两次标定沿轨方向指向差异小于0.1像元,92.68%的样本探元两次标定垂轨方向指向差异小于0.2像元,沿轨方向中误差小于0.03像元,垂轨方向中误差小于0.07像元。两次在轨标定结果稳健一致,直接证明了本文标 定模型和求解算法的稳定性,一定程度上从侧面反映了本文标定方法的正确性。
3.3 内参数在轨标定前后定位精度对比实验内参数在轨标定结果定位精度的验证,传统方法是采用不同检校场验证,即采用某一检校场实施在轨标定,而采用其他检校场进行结果验证。该方法对检校场数据要求严格,即应具有多个(至少两个)检校场的控制数据。
对于仅具备单一检校场,但同时具备该检校场多次观测影像的情况,虽然检校场数据是静态不变的,但不同成像日期的多次观测是动态变化的。这种情况下可采用多次观测数据交互验证的方法对内参数在轨标定结果进行验证。
本文具备单一检校场的多次观测数据,因此采用多次观测数据交互验证的方法对内参数在轨标定结果进行验证,即在135-1影像上验证135-2的内参数标定结果,而在135-2影像上验证135-1的内参数标定结果。
具体步骤如下:
1) 相机内参数分别采用实验室标定值和135-2在轨标定值,在135-1影像上选取“四角+中心”5个控制点计算其偏置矩阵,剩余控制点作为检查点,对比内参数在轨标定前后135-1影像的像方定位精度;
2) 相机内参数分别采用实验室标定值和135-1在轨标定值,在135-2影像上选取“四角+中心”5个控制点计算其偏置矩阵,剩余控制点作为检查点,对比内参数在轨标定前后135-2影像的像方定位精度。
实验结果如表3所示。
| 验证影像 | 所采用的内参数 | 沿轨方向/像素 | 垂轨方向/像素 | ||||
| 最小 | 最大 | RMS | 最小 | 最大 | RMS | ||
| 135-1 | 实验室标定值 135-2在轨标定值 | 0.004 0.004 | 0.903 0.869 | 0.455 0.395 | 0.426 0.079 | 2.361 1.028 | 1.458 0.538 |
| 135-2 | 实验室标定值 135-1在轨标定值 | 0.019 0.038 | 1.071 0.858 | 0.626 0.543 | 0.296 0.021 | 2.807 0.850 | 1.495 0.465 |
分析表3可发现,经内参数在轨几何标定,135-1影像的像方定位精度沿轨方向由0.455像元提升至0.395像元,垂轨方向由1.458像元提升至0.538像元;135-2影像的像方定位精度沿轨方向由0.626像元提升至0.543像元,垂轨方向由1.495像元提升至0.465像元。总体而言,经内参数在轨标定,沿轨方向的定位精度略有提升,垂轨方向的定位精度提升显著,与标定出的沿轨、垂轨畸变程度保持一致。
4 结 语本文基于偏置矩阵和探元指向角构建了线阵推扫式相机的在轨标定模型,并给出了相应的参数求解方法。对相机物理模型到指向角模型的过程进行了推导,分析了偏视场相机与正视场相机在使用指向角模型时的不同,并分别给出了两者的具体计算公式。利用嵩山检校场高精度控制数据和天绘一号高分影像对本文的标定模型和求解方法进行了验证,对标定前后影像的定位精度进行了对比分析。通过实验分析得出如下结论:
1) 采用偏置矩阵外标定模型和指向角内标定模型,配合先外后内、分步求解的策略有利于克服参数间的相关性,可实现线阵推扫式相机的在轨高精度几何标定。
2) 正视场相机和偏视场相机的指向角模型略有不同,在使用时需注意。
3) 选取沿线阵CCD方向分布均匀、沿飞行方向分布集中的控制方案,采用本文的标定模型和求解算法,有利于标定出稳健可靠的相机内参数。
4) 当仅具备单一检校场控制数据时,可通过该区域不同时期多次观测影像交互验证的方法对标定结果进行验证。
5) 与实验室标定的内参数相比,采用本文在轨标定出的内参数,影像定位精度显著提高,利用“四角+中心”的控制方案计算各景影像的偏置矩阵后,影像定位精度可达子像素级。
| [1] | Zhang Yongsheng, Gong Danchao, Liu Jun. Application of High Resolution Remote Sensing Satellite [M]. Beijing: Science Press, 2004:10-12(张永生, 巩丹超, 刘军. 高分辨率遥感卫星应用[M].北京: 科学出版社, 2004:10-12) |
| [2] | Ebner H, Kornus W, Strunz G, et al. Simulation Study on Point Determination Using MOMS_O2/D2 Imagery[J]. Photogrammetric Engineering & Remote Sensing, 1991, 57(10): 1 315-1 320 |
| [3] | Jacobsen K. Issues and Method for In-Flight and On-Orbit Calibration[C]. Workshop on Radiometric and Geometric Calibration,Gulfport, Mississippi,USA, 2003 |
| [4] | Srivastava P K, Alurkar M S. In-Flight Calibration of IRS-1C Imaging Geometry for Data Products[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1997, 52(7): 215-221 |
| [5] | Kornus W, Lehner M. Geometric In-Flight Calibration of the Stereoscopic CCD-Line Scanner MOMS-2P[C]. ISPRS Com I Symp, Bangalore,India,1998 |
| [6] | Valorge C. 40 Years of Experience with SPOT In-Flight Calibration[C].Workshop on Radiometric and Geometric Calibration, Gulfport, Mississippi,USA, 2003 |
| [7] | Gene D, Grodecki J. IKONOS Stereo Accuracy Without Ground Control[C]. ASPRS 2003 Conference,Anchorage,Alaska, USA, 2003 |
| [8] | Zhang Li, Zhang Jixian, Chen Xiangyang, et al. Block-Adjustment with SPOT5 Imagery and Sparse GCPs Based on RFM [J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 302-310(张力, 张继贤, 陈向阳, 等. 基于有理多项式模型RFM的稀少控制SPOT5卫星影像区域网平差[J]. 测绘学报, 2009, 38(4): 302-310) |
| [9] | Grodecki J, Lutes J. IKONOS Geometric Calibrations[C]. ASPRS 2005, Baltimore, Maryland, 2005 |
| [10] | Fraser C S,Baltsavias E,Gruen A. Processing of IKONOS Imagery for Submetre 3D Positioning and Building Extraction[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2002, 56(3): 177-194 |
| [11] | Baltsavias E, Zhang L,Eisenbeiss H. DSM Generation and Interior Orientation Determation of IKONOS Images Using a Testfield in Switzerland[J]. Photogrammetrie Fernerkundung Geoinformation, 2006, 60(1): 41-54 |
| [12] | Gruen A, Kocaman S, Wolff K. Calibration and Validation of Early ALOS/PRISM Images[J]. The Journal of the Japan Society of Photogrammetry and Remote Sensing, 2007, 46(1): 24-38 |
| [13] | Tadono T, Shimada M, Watanabe M, et al. Calibration and Validation Plan of ALOS Optical Sensors[C].Geoscience and Remote Sensing Symposium,Anchorage,AK, 2004 |
| [14] | Wang Renxiang. Satellite Photogrammetry Princple for Three-Line-Array CCD Imagery[M]. Beijing: Surveying and Mapping Press, 2006:20-23(王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京: 测绘出版社, 2006:20-23) |
| [15] | Li Jing, Wang Rong, Zhu Leiming, et al. In-Flight Geometric Calibration for Mapping Satellite-1 Surveying and Mapping Camera[J]. Journal of Remote Sensing, 2012, 16(z1): 35-39(李晶, 王蓉, 朱雷鸣, 等. “天绘一号”卫星测绘相机在轨几何标定[J].遥感学报, 2012, 16(z1): 35-39) |
| [16] | Xu Jianyan, Hou Minghui, Yu Jin, et al. Study of CBERS CCD Camera Bias Matrix Calculation and Its Application[J]. Spacecraft Recovery & Remote Sensing, 2004(4):25-29(徐建艳, 侯明辉, 于晋,等. 利用偏移矩阵提高CBERS 图像预处理几何定位精度的方法研究[J]. 航天返回与遥感, 2004(4):25-29) |
| [17] | Zhu Xiaoyong, Zhang Guo, Tang Xinming, et al. Research and Application of CBRS02B Image Geometric Exterior Calibration[J]. Geography and Geo-Information Science, 2009, 25(3): 16-18(祝小勇, 张过, 唐新明, 等. 资源一号02B卫星影像几何外检校研究及应用[J]. 地理与地理信息科学, 2009, 25(3): 16-18) |
| [18] | Yuan Xiuxiao, Yu Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 36-41(袁修孝, 余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报, 2008, 37(1): 36-41) |
| [19] | Yuan Xiuxiao, Yu Xiang. Calibration of Angular Systematic Errors for High Resolution Satellite Imagery [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 385-392(袁修孝, 余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报, 2012, 41(3): 385-392) |
| [20] | Lei Rong. Study on Theory and Algorithm of the In-Flight Geometric Calibration of Spaceborne Linear Array Sensor[D]. Zhengzhou: Information Engineering University, 2011(雷蓉. 星载线阵传感器在轨几何标定的理论与算法研究[D]. 郑州: 信息工程大学, 2011) |
| [21] | Wang Tao. Study on Theories and Methods of Linear CCD Sensor Geometric Calibration Based on Field[D]. Zhengzhou: Information Engineering University, 2012(王涛. 线阵CCD传感器实验场几何标定的理论与算法研究[D]. 郑州: 信息工程大学, 2012) |
| [22] | Hao Xuetao, Xu Jianyan, Wang Haiyan, et al. An Angle-based Method of On-Orbit Geometric Calibration for the Pushbroom Camera[J]. Scientia Sinica: Informationis,2011, 41(zk): 10-18 (郝雪涛, 徐建艳, 王海燕, 等. 基于角度不变的线阵推扫式CCD相机几何畸变在轨检校方法[J]. 中国科学: 信息科学, 2011, 41(增刊): 10-18) |
| [23] | Yang Bo, Wang Mi. On-Orbit Geometric Calibration Method of ZY-1 02C Panchromatic Camera[J]. Journal of Remote Sensing, 2013, 17(5):1 183-1 190(杨博, 王密. 资源一号02C卫星全色相机在轨几何标定方法[J]. 遥感学报, 2013, 17(5):1 183-1 190) |
| [24] | Wang Mi, Yang Bo, Hu Fen,et al. On-Orbit Geometric Calibration Model and Its Applications for High-Resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4 391-4 408 |
| [25] | Jiang Yonghua, Zhang Guo, Tang Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three Line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529(蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523-529) |
| [26] | Tang Xinming, Zhang Guo, Zhu Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198(唐新明, 张过, 祝小勇,等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191-198) |
| [27] | Liu Bin.Space-ground Intergated Attitude Determination of High-resolution Satellite and Geometric Image Processing Under Jitter Conditions[D]. Wuhan: Wuhan University, 2011(刘斌.高分辨率光学卫星空地一体化定姿及姿态抖动下影像几何处理方法研究[D]. 武汉: 武汉大学, 2011) |
| [28] | Zhang Guo,Jiang Yonghua, Li Deren, et al. In-Orbit Geometric Calibration and Validation of ZY-3 Linear Array Sensors [J]. Photogrammetric Record, 2014, 29(145): 68-88 |
 2015, Vol. 40
2015, Vol. 40