文章信息
- 贾剑钢, 栾威, 申文斌
- JIA Jiangang, LUAN Wei, SHEN Wenbin
- iGrav-007超导重力仪格值的精密测定
- Accurate Determination of the Calibration Factor of iGrav-007 Superconducting Gravimeter
- 武汉大学学报·信息科学版, 2015, 40(10): 1366-1370,1376
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1366-1370,1376
- http://dx.doi.org/10.13203/j.whugis20130780
-
文章历史
- 收稿日期: 2014-07-04

2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
超导重力仪(superconducting gravimeter,SG)被认为是观测精度最高、稳定性和连续性最好的地球重力信号观测仪器,对重力场变化的灵敏度很高,广泛应用于时变重力场研究[1, 2, 3]。1997年7月启动的全球地球动力学计划(global geodynamics projects,GGP)为研究全球地球动力学现象,包括固体地球重力潮汐、重力场与海洋大气的耦合效应、地球自由核章动、固态内核的平动振荡、固态地幔的自由振荡、地球自转变化和长期地壳运动等导致的重力效应提供了全球超导重力仪观测资料[2, 3],该计划的实施即利用全球超导重力仪观测网络获得的重力场时变研究地球物理学和地球动力学中的国际焦点问题[4, 5, 6]。因超导重力仪的原始观测值为重力反馈电压,需对其进行格值标定才能转换为重力值,故超 导重力仪格值的精密测定是利用其高精度观测数据反演地球物理学现象的必要前提,当前潮汐模型的优化要求该项格值的标定精度为0.1%的量级或更高[7, 8]。
本文基于最小二乘线性回归和迭代算法,采用比测法[9],利用FG5-112绝对重力仪(absolute gravimeter,AG)与iGrav-007超导重力仪于2013年在武汉九峰台站连续3天的同址、同期观测,精密测定iGrav-007的格值,并分析仪器漂移和比测数据个数对格值及精度的影响;基于iGrav-007连续5个月的观测数据,采用线性拟合和最小二乘滤波分析仪器漂移和观测精度,验证格值标定的准确性。
1 AG和SG同址观测及精度评定方法 1.1 同址观测FG5绝对重力仪由美国Micro-g公司生产,该仪器基于自由落体原理测量垂直加速度,设计精度达(1~2)×10-8 m/s2,是目前世界上精度最高的绝对重力仪[10]。中国科学院测量与地球物理研究所于1995年引进了一台FG5-112,1996年FG5-112在中国大陆中西部15个绝对重力点的观测精度为(0.81~2.78) ×10-8 m/s2[11];2010年在武汉组织的国内所有FG5比测试验中,FG5-112的观测精度为(1.4~2.0)×10-8 m/s2[12],两次试验结果表明FG5-112保持着较高的稳定性,保证了对iGrav-007格值标定的准确性。
iGrav超导重力仪由美国GWR仪器公司生产,以稳恒超导电流为核心的工作原理使其具有极高的稳定性:零漂小于0.5 μGal/月,是目前世界上最稳定的相对重力仪。与广泛应用于世界各地地球动力学研究项目的OSG超导重力仪相比,iGrav设计简单,价格略低,易于使用;其观测灵敏度在频域中为1 nanoGal(1×10-9 Gal),在时域中1 min平均值为0.05 μGal[13]。武汉大学于2012年引进了一台iGrav-007,2013年3月安装于武汉九峰观测站。
为获得高精度的iGrav-007的格值,2013年6月20日23:30:00至24日01:19:55,在武汉九峰观测站进行了长约74 h的与FG5-112同址、同期观测。两台仪器平行架设于观测室内,相距不到10 m,观测环境基本保持一致,测点重力场变化几近相同。
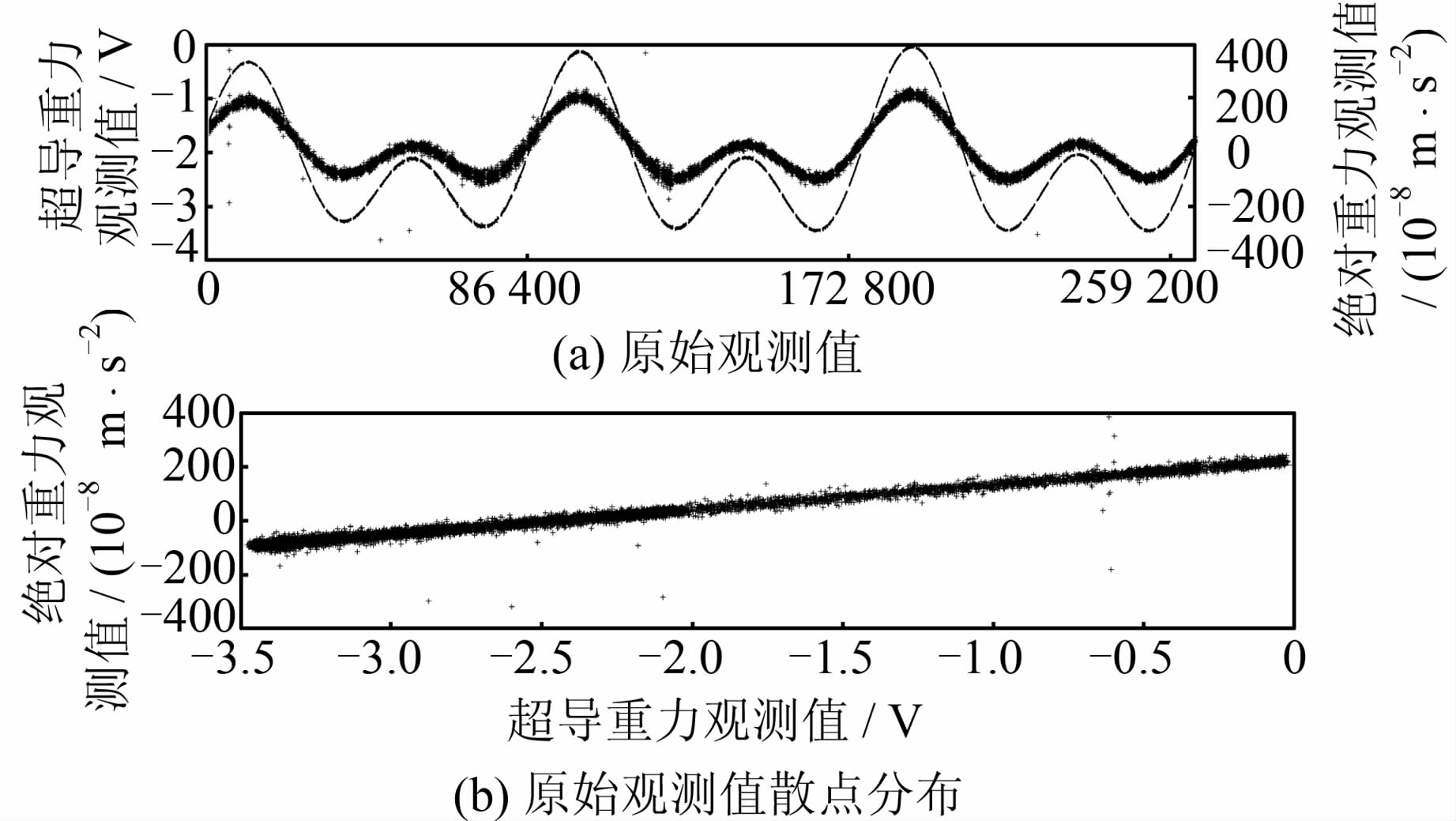
FG5-112采用如下观测方案:每50 min观测一组,每组落体次数为150次,单次落体的观测时间为20 s,除开始两组之间停测10 min 15 s,其他均为每50 min停测10 min,故总共74组落体观测,理论上可获得11 100个观测值。iGrav-007采样率为1 Hz。由于FG5获取的观测值gnontide已剔除了固体潮gtide和海潮gocean的影响,为了便于比较,用gnontide+gtide+gocean-G(G为FG5-112所在绝对重力点的多年平均重力值,为一常数)来获得重力变化值。图 1(a)给出了比测期间FG5-112(用“+”表示的粗线,单位为10-8 m/s2,且为了与超导重力仪相比较,观测值已乘以-1)和iGrav-007(用“·”表示的细线,单位为V,且只保留与FG5-112数据获取时刻一致的观测数据)的原始观测值。可见比测期间潮汐变化较大,这对于使格值快速达到所需的精度更有利[14];比测期间仪器数据记录良好,且无间断现象,iGrav-007观测十分平滑,而FG5-112有许多离散值,这些离散值的误差源包括激光问题、时钟漂移、环境或微震噪声等[15],在计算格值时须剔除。
|
| 图 1 FG5-112、iGrav-007原始观测值和原始 观测值散点分布 Fig. 1 Original Observations and Scatter Distribution of Original Observations of FG5-112 and iGrav-007 |
从图 1(b)散点分布图可见,样本点呈条状分布,两个时间序列观测值呈良好的线性关系。设自变量V(t)为iGrav-007的观测值(单位V),因变量y(t)为FG5-112的观测值(单位10-8m/s2),根据样本相关系数计算公式:
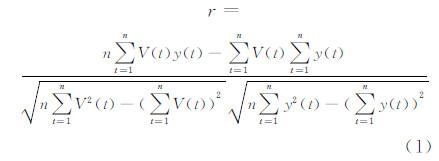
算得样本点的相关系数为-0.991 4,判定两变量为高线性的负相关,故可采用如下一元线性回归模型:
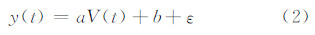
式中,a、b为线性回归系数,且a为超导重力仪的格值(单位10-8 m·s-2/V)。
为使估计直线 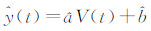 最佳拟合于绝对重力观测值,应使各观测点到该直线的偏差平方和最小,即要求a、b的估值使
最佳拟合于绝对重力观测值,应使各观测点到该直线的偏差平方和最小,即要求a、b的估值使
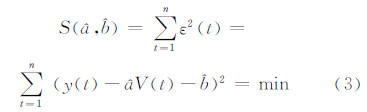
取微分,解得回归系数最小二乘估计 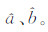 。令
。令 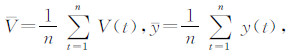 ,有:
,有:
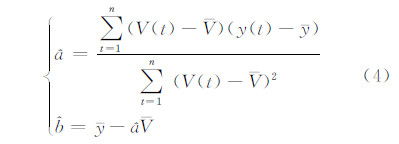
由于 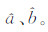 是根据有误差的观测数据点算得的,无法避免偏差的存在,且各观测数据点并非都与拟合线准确重合,绝对重力观测值y(t)与对应于拟合直线上的 (t)间也有偏差。为衡量所有随机误差对y(t)的平均偏差大小,需计算残差标准差σ:
是根据有误差的观测数据点算得的,无法避免偏差的存在,且各观测数据点并非都与拟合线准确重合,绝对重力观测值y(t)与对应于拟合直线上的 (t)间也有偏差。为衡量所有随机误差对y(t)的平均偏差大小,需计算残差标准差σ:
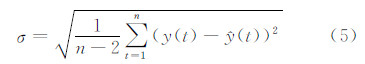
σ越小,回归直线的精度越高,当回归方程的稳定性较好时,σ可作为回归方程的精度参数。下文迭代计算中,在未知观测值中误差的情况下,用残余标准差替代中误差。
对于超导重力观测值V(t)误差的处理方法是分析V(t)在实际测量中可能出现的误差限,再根据自变量和因变量的回归方程,将V(t)误差限转变成变量y(t)的一个不确定度B分量,与变量y(t)的其他不确定度A分量进行合成处理。故在推导回归系数时,可不考虑V(t)的误差。由iGrav-007和FG5-112的观测方式可知,对被观测量V、y分别进行了多次等精度观测,用V(t)、y(t)(t=1,2,…,n)表示观测值。观测y时,存在A分量σ2(方差)和B分量u2(该项主要 与iGrav-007的观测精度有关)。因iGrav-007的噪声水平很低,观测精度高于FG5-112 至少2个量级[16],故此处将自变量 V(t)当做准确值,所有的误差只与y(t)有关,即B分量近似为零,则y的不确定度uy可以表示为:
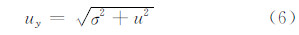
根据不确定度传递公式得:
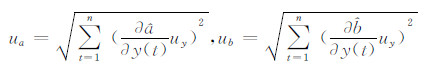
将式(4)分别代入ua、ub,可算得:
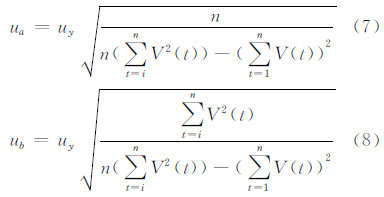
则相对不确定度分别为:
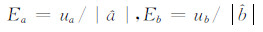
由于超导重力仪振幅因子估算的精度和目前潮汐模型参数的相对精度均为0.1%的量级或更高,因此格值标定的相对精度要求在0.1%的量级。为此,在线性回归运算中,采用3倍中误差(3σ)作为观测限差剔除异常数据[14, 16, 17]。孙和平等[6]的研究表明,当观测限差在(20~35)×10-8m/s2之间,参与计算的观测数据对个数在7 000以上,格值的变化在0.3%范围内。因FG5-112 观测值中出现了若干明显的错误数据,影响了线性回归计算,故本文剔除了其中绝对值大于600×10-8 m/s2的96个数据。对FG5-112和iGrav-007原始观测数据作最小二乘线性回归计算,回归系数 =-91.672 0×10-8 m\5s-2/V,残差标准方差σ=12.483 2×10-8 m/s2,可确定观测限差超出范围,说明异常 数据的剔除非常必要。
采用最小二乘线性回归方法,以残差标准差(σ)为中误差,以3σ为剔除异常数据的限差,当格值的变化小于0.001时停止迭代,实际计算中迭代7次即可。由于同址观测时间较短,且仪器长期漂移通常表现为线性漂移[14],对参与计算的观测数据进行线性拟合,比较拟合直线的斜率,如图 2所示。每次迭代运算中都去掉重力观测值的线性部分(包括仪器漂移、潮汐和大气变化的趋势项)。参与格值计算的重力观测值共10 865对,FG5-112的数据利用率约为97.88%;iGrav-007、FG5-112观测值的线性拟合斜率分别为-0.000 002 94、-0.000 270,观测时段内的线性偏移量分别为-0.782 5 V和71.680 5× 10-8 m/s2,最终算得线性回归残差标准差为9.150 796×10-8 m/s2。比较仪器漂移影响去除前后可知,3天的仪器漂移对回归残差标准差的变化量很小,对回归直线精度的影响也小到可以忽略。但若同址观测时间更长,在进行格值计算前,须去除仪器漂移,并注意异常数据的影响。本文忽略漂移的影响,得到iGrav-007的格值为(-91.640 2± 0.085 2)×10-8 m·s-2/V,相对标定精度为0.092 9%。图 3给出了剔除异常数据后仪器同址观测期间FG5-112和iGrav-007观测值之间的比较,可见经过最小二乘线性迭代回归计算后,观测残差很好地收敛于观测限差范围内。
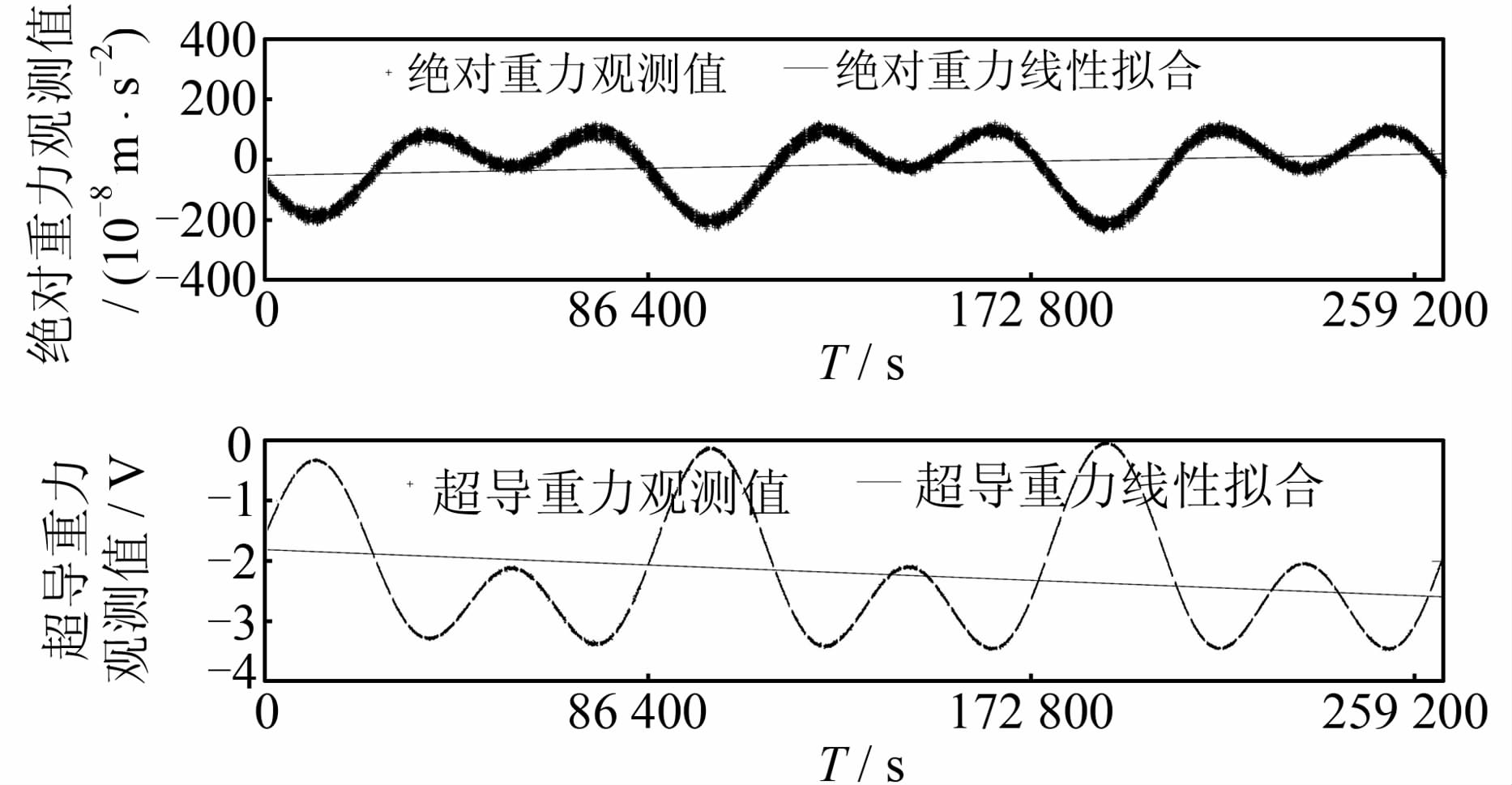
|
| 图 2 FG5-112和iGrav-007的线性漂移 Fig. 2 Linear Instrument Drifts of FG5-112 and iGrav-007 |
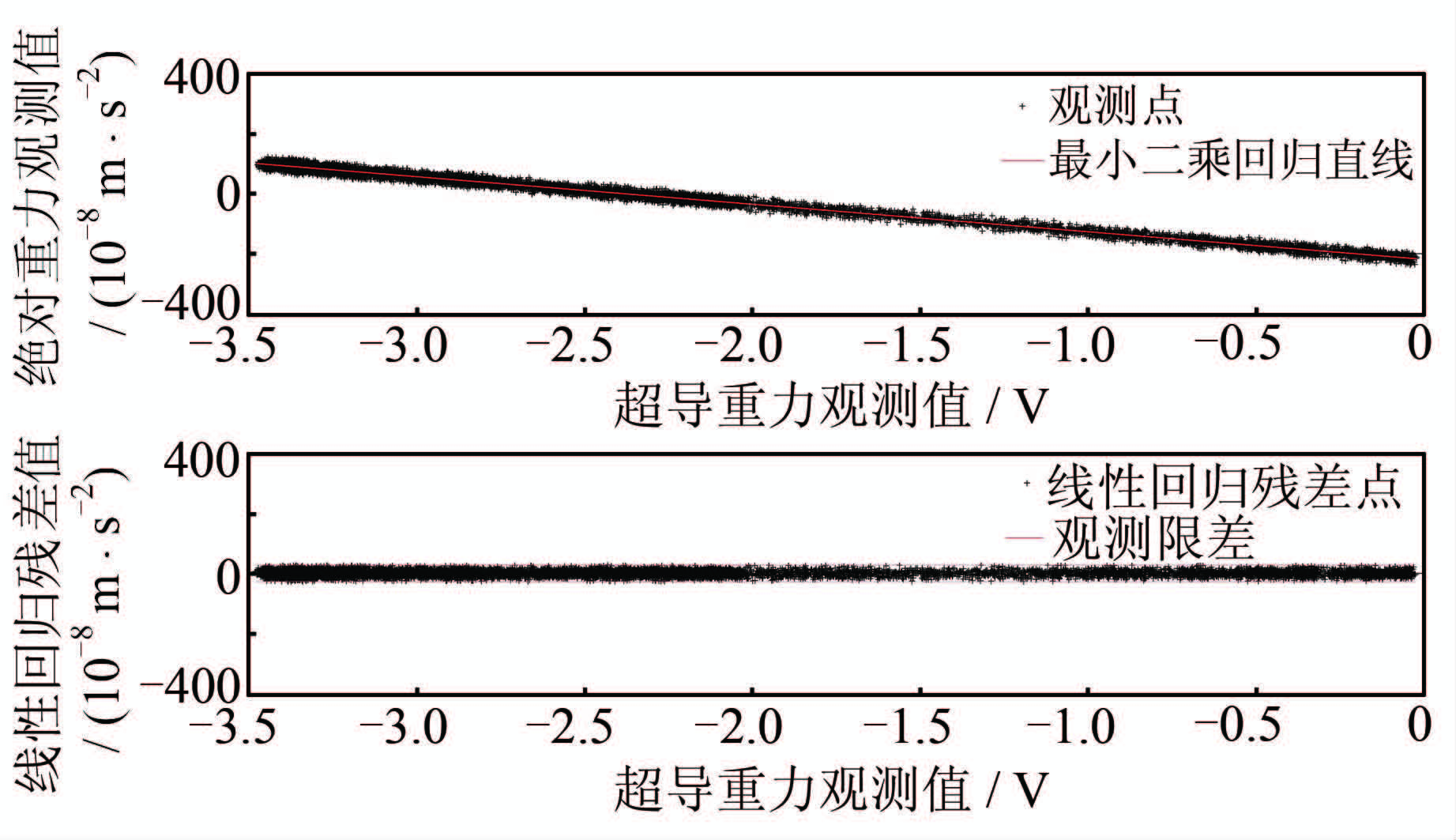
|
| 图 3 FG5-112和iGrav-007观测值之间的比较 Fig. 3 Comparison Between the Observations of FG5-112 and iGrav-007 |
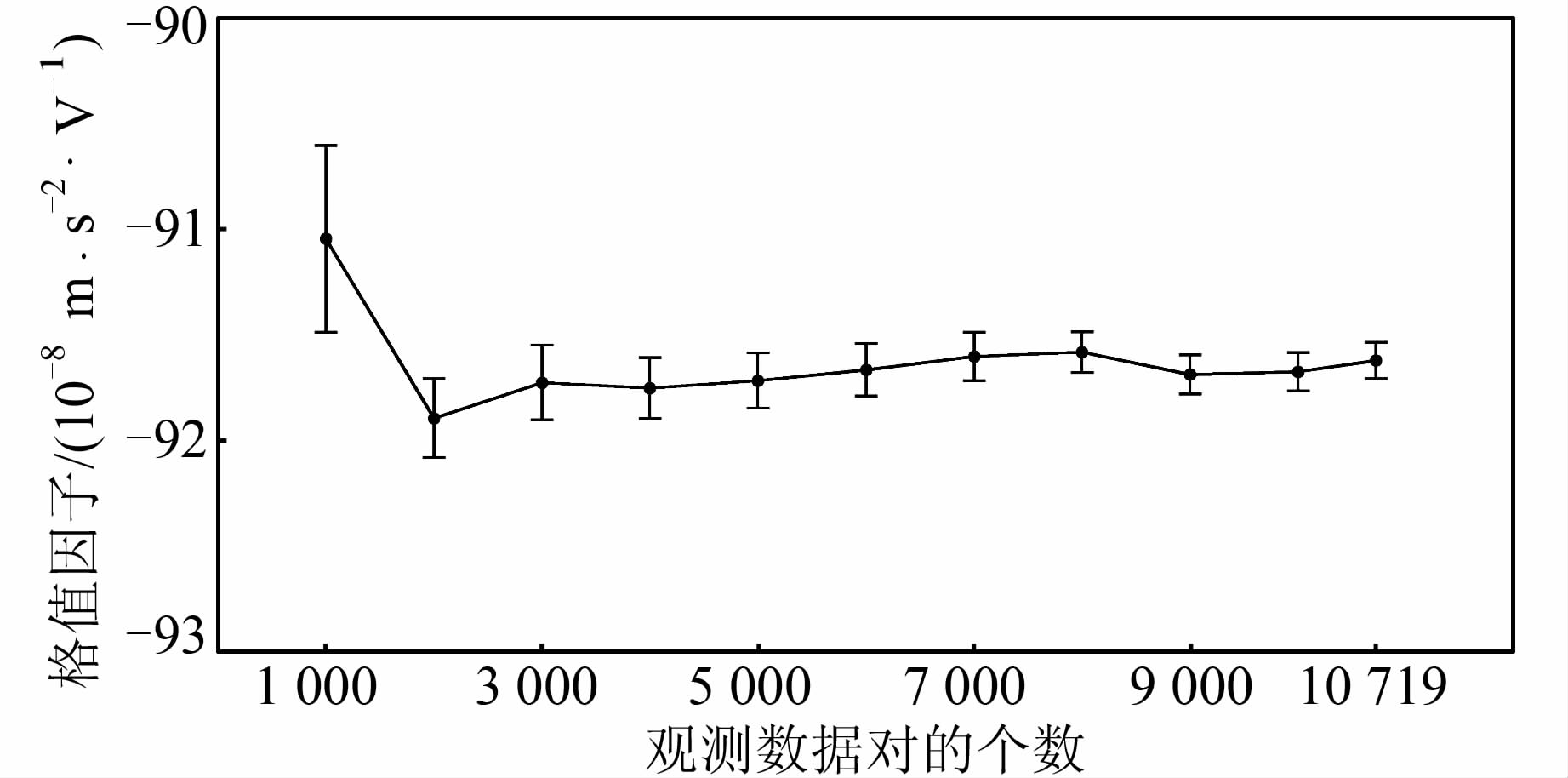
为比较不同落体次数对格值的影响,利用选用的10 865对观测数据,按不同的落体次数分段进行格值计算。表 1给出了不同个数的观测数据获得的格值及其精度,图 4给出了所测定的格值与观测数据对个数间的关系。当观测数据对个数超过3 000时,获得的格值和精度趋于稳定,相对标定精度优于0.2%。因此当选用FG5标定iGrav时,若按20 s一次落体,每观测50 min停测10 min的方案,至少需要20 h的有效观测数据;若要满足格值相对标定精度优于0.1%,至少需要连续67 h的有效观测数据,考虑到实际观测数据中总存在异常数据,连续3天的同址观测才能满足格值的精度要求。
| 观测数据对个数 | 格值/(10-8 m·s-2\5V-1) | 相对标定精度/% |
| 1 000 | -91.592 5±0.631 9 | 0.697 6 |
| 2 000 | -91.933 2±0.183 3 | 0.199 3 |
| 3 000 | -91.846 7±0.173 7 | 0.189 1 |
| 4 000 | -91.878 6±0.151 4 | 0.164 8 |
| 5 000 | -91.705 1±0.132 3 | 0.144 3 |
| 6 000 | -91.689 2±0.122 2 | 0.133 2 |
| 7 000 | -91.625 9±0.112 0 | 0.122 3 |
| 8 000 | -91.611 1±0.096 8 | 0.105 7 |
| 9 000 | -91.702 3±0.092 2 | 0.100 5 |
| 10 000 | -91.716 0±0.089 6 | 0.097 7 |
| 10 865 | -91.640 2±0.085 2 | 0.092 9 |
|
| 图 4 格值与观测数据对个数之间的关系 Fig. 4 Relation Between the Calibration Factor and the Number of Pairs of Data |
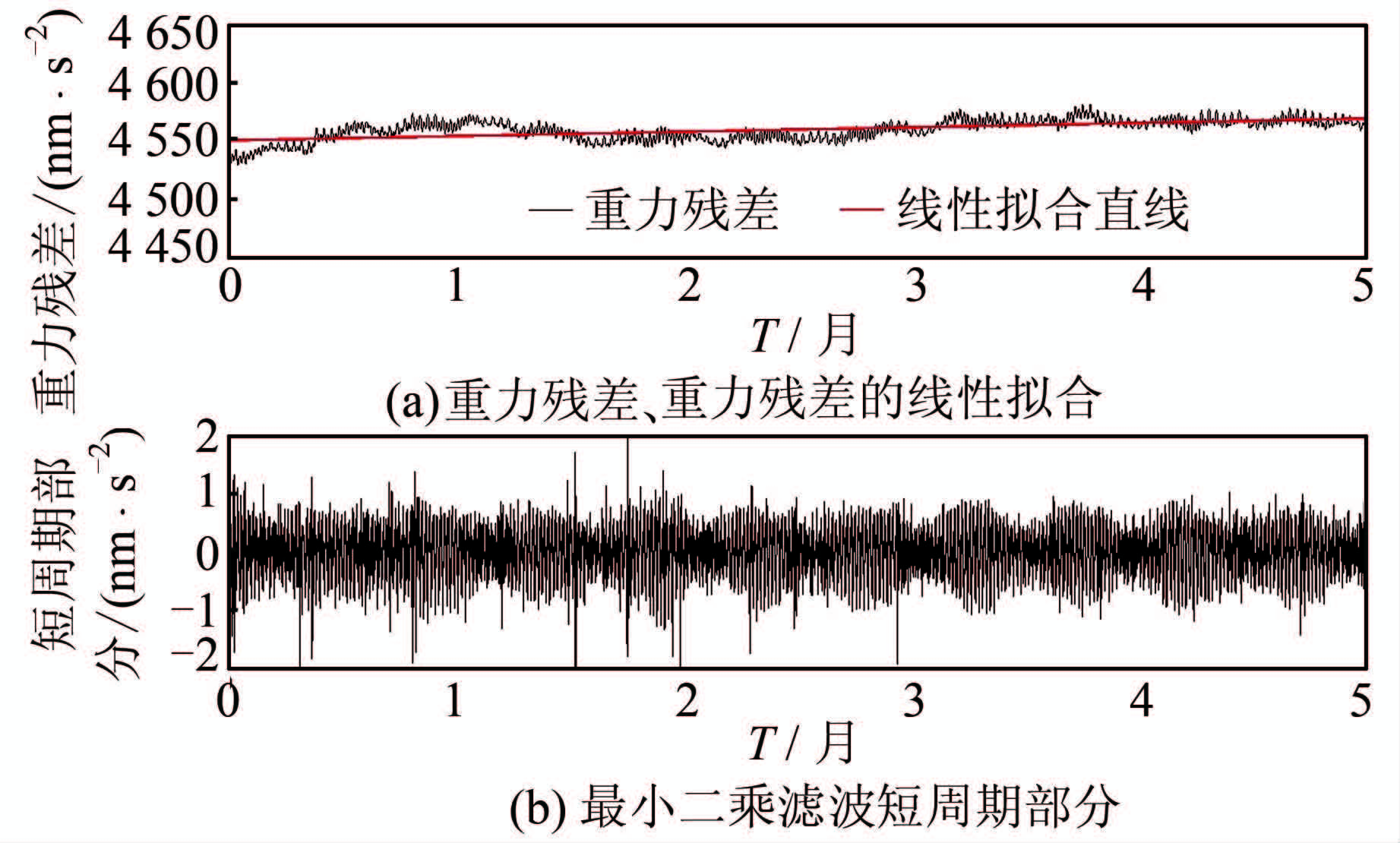
根据上文确定的iGrav-007的格值因子,选取仪器安装后连续5个月(仪器安装后3个月内处于调试阶段,尚不稳定,故此处选取的时间段为2013-06-25~2013-11-25)的采样观测数据。经过潮汐、气压和极移改正等预处理得到重力残差,线性拟合得iGrav-007的漂移率为0.375 μGal /月,如图 5(a)所示,该结果小于其标称值0.50 μGal/月,表明iGrav-007具有极高的稳定性;采用最小二乘高通滤波器处理重力残差,如图 5(b)所示,取截止频率为合成潮M3波的最高频率3.081 254 cpd,认为高于M3波频的部分(短周期部分)为仪器的高频噪声所致,取短周期部分扣除平均值后的均方根(RMS)作为iGrav-007的观测精度,为0.038 μGal/min,该结果小于其标称值0.05 μGal /min,表明iGrav-007具有较高精度的观测性能。该结果也进一步验证了iGrav-007格值标定的准确性。
|
| 图 5 iGrav-007连续5个月(2013年6月25日- 11月25日)的重力残差、重力残差的线性 拟合以及最小二乘滤波短周期部分 Fig. 5 Gravity Residuals, the Linear Fitting of the Gravity Residuals and the Short Cycle Part of the Least Squares Filtering Results of iGrav-007 for 5 Months (June 25th-November 25th,2013) |
在大潮期间,利用运行状态良好的绝对重力仪观测能够精确有效地测定超导重力仪的格值。考虑3天中呈线性变化的仪器漂移对格值精确测定的影响,利用武汉九峰台站FG5-112与iGrav-007连续3天的同址观测结果测定iGrav-007的格值为(-91.640 2±0.085 2)×10-8 m·s-2/V,相对标定精度为0.092 9%。24 h的标定精度优于法国Hinderer[7]获得的精度(0.72%),72 h的优于孙和平[6]获得的精度(0.2%),连续3天的精度优于0.1%量级,与Francis[17]利用连续9天获得的精度(0.08%)、邢乐林等[19]利用连续5天获得的精度(0.11%)为同一量级[18]。选取 iGrav-007安装后5个月的连续观测数据初步分析该仪器的漂移量和观测精度,认为其具有极高的稳定性和高精度的观测性能,也验证了格值标定的准确性。
致谢:感谢中国科学院测量与地球物理研究所提供的FG5-112绝对重力仪观测数据,以及陈晓东副研究员等的悉心指导和帮助。
| [1] | Goodkind J M. The Superconducting Gravimeter[J].Review of Scientific Instruments, 1999, 70(11): 4 132 -4 152 |
| [2] | Hinderer J, Crossley D.Scientific Achievements from the First Phase (1997-2003) of the Global Geodynamics Project Using a Worldwide Network of Superconducting Gravimeters[J]. Journal of Geodynamics, 2004, 38(3):237-262 |
| [3] | Crossley D, Hinderer J. Report of GGP Activities to Commission 3, Completing 10 Years for the Worldwide Network of Superconducting Gravimeters[M]//Observing Our Changing Earth. Berlin, Heidelberg: Springer, 2009 |
| [4] | Sun Heping,Xu Houze.The Implementation and Prospection of the International Geodynamics Cooperation Projects[J]. Advance in Earth Sciences,1997,12(2):152-157(孙和平,许厚泽. 国际地球动力学合作项目的实施与展望[J]. 地球科学进展, 12(2):152-157) |
| [5] | Sun Heping, Chen Xiaodong, Xu Houze, et al. Precision Measurement of the Calibration Factor by GWR Superconducting Gravimeter Tidal Observation[J]. Acta Seism-Ologica Sinica, 2001,23(6):651-658(孙和平, 陈晓东,许厚泽,等. GWR超导重力仪潮汐观测标定因子的精密测定[J]. 地震学报,2001,23(6):651-658) |
| [6] | Shen Wenbin,Liu Renli. Study of Detecting the Inner Core Super Rotation Using SG Data[J]. Geomatics and Information Science of Wuhan University,2009, 34(1):72-76(申文斌,刘任莉. 利用超导重力数据探测内核超速旋转的研究[J].武汉大学学报·信息科学版,2009, 34(1):72-76) |
| [7] | Hinderer J. On the Calibration of a Super Conducting Gravimeter Using Absolute Gravity Measurements[J].Geophysical Journal International, 1991, 106(2):491-497 |
| [8] | Baker T F, Bos M S. Validating Earth and Ocean Tide Models Using Tidal Gravity Measurements[J]. Geophys J Int, 2003, 152(2):468-485 |
| [9] | Francis O, Van Dam T. Evaluation of the Precision of Using Absolute Gravimeters to Calibrate Superconducting Gravimeters[J]. Metrologia, 2002, 39(5):485-488 |
| [10] | Neibauer T M, Klopping F J, Faller J E. The FG5 Absolute Gravimeter[J]. Bur Grav Int Bull d'Inf Toulouse, 1995(11):1-2 |
| [11] | Wang Yong, Xu Houze,Zhang Weimin, et al. High Precision Absolute Gravity Observations in the Midwest of China in 1996[J]. Chinese Journal of Geophysics, 1998, 41(6): 818-825(王勇, 许厚泽, 张为民, 等. 1996年中国中西部地区高精度绝对重力观测结果[J]. 地球物理学报, 1998,41(6): 818-825) |
| [12] | Xiao Fan,Zhang Hongwei,Wang Yingjian, et al. Analysis of FG5 Absolute Gravimeter Comparison Observation Data[J]. Hydrographic Surveying and Charting, 2011, 5(31): 55-57(肖凡, 张宏伟, 王应建, 等. FG5绝对重力仪比对观测数据分析. 海洋测绘, 2011, 5(31): 55-57) |
| [13] | Warburton R J, Pillai H, Reineman R C. Initial Results with the New GWR iGravTM Superconducting Gravity Meter[C]. International Association of Geodesy (IAG) Symposium Proceedings, Saint Petersburg, Russia, 2010 |
| [14] | Chen Xiaodong, Sun Heping, Zhang Weimin,et al. Precision Analysis of the Determination of Superconducting Gravimeter Calibration Factor with Absolute Gravimeter[J]. Journal of Geodesy and Geodynamics,2013,33(5):145-149(陈晓东, 孙和平, 张为民, 等. 用绝对重力仪测定超导重力仪格值的精度分析[J]. 大地测量与地球动力学, 2013,33(5):145-149) |
| [15] | Van Camp M, Williams S D P, Francis O. Uncertainty of Absolute Gravity Measurements[J]. J Geophys Res,2005,110:B05406, doi:10.1029/2004JB003497 |
| [16] | Riccard U, Rosat S, Hinderer J. On the Accuracy of the Calibration of Superconducting Gravimeters Using Absolute and Spring Sensors: A Critical Comparison[J]. Pure Appl Geophys, 2011,169(2 012):1 343-1 356 |
| [17] | Francis O. Calibration of a Superconducting Gravimeter by Comparison with an Absolute Gravimeter FG5 in Boulder[J]. Geophysical Research Letters,1998, 25(7):1 075-1 078 |
| [18] | Xing Lelin,Li Hui, Liu Ziwei, et al. Precise Determination of Superconducting Gravimeter Calibration Factor by Absolute Gravity Measurement[J]. Journal of Geodesy and Geodynamics, 2010, 30(1):48-50(邢乐林,李辉,刘子维,等. 利用绝对重力测量精密测定超导重力仪的格值因子[J]. 大地测量与地球动力学, 2010, 30(1):48-50) |
 2015, Vol. 40
2015, Vol. 40


