文章信息
- 曾小牛, 刘代志, 李夕海, 苏娟, 陈鼎新, 齐玮
- ZENG Xiaoniu, LIU Daizhi, LI Xihai, SU Juan, CHEN Dingxin, QI Wei
- 一种改进的病态问题奇异值修正法
- An Improved Singular Value Modification Method for Ill-posed Problems
- 武汉大学学报·信息科学版, 2015, 40(10): 1349-1353
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1349-1353
- http://dx.doi.org/10.13203/j.whugis20130709
-
文章历史
- 收稿日期: 2013-11-26

诸多学科与工程技术领域都存在病态方程[1]。为了解算这类病态方程,许多学者提出和发展了各种有效的数值方法。这些方法可分为两类[2]:直接法和迭代法。直接法中最著名的是Tikhonov正则化方法[3]和截断奇异值(truncated singular value decomposition,TSVD)正则化方法[4]。常见的迭代法有最速下降法、牛顿迭代法和共轭梯度迭代法等[5]。在对观测方程的系数矩阵进行谱分解后,所有正则化方法都可以对应一个对奇异值进行修正的正则化滤波函数[6]。文献[7]基于系数矩阵的谱分解从理论上阐述了Tikhonov与TSVD这两种正则化方法的效果的差异;文献[8]提出的两步解法中对合适正则化矩阵的选取,其本质也可归纳到对奇异值更好的修正上;文献[9]将系数矩阵相对较大和相对较小的奇异值区别对待,综合Tikhonov奇异值修正法和截断奇异值法的特点提出了改进的奇异值修正法。本文结合Gaussian滤波函数和Tikhonov滤波函数提出了一种改进的病态问题奇异值修正法——Tikhonov-Gaussian法。
1 病态方程的谱分解观测方程的一般形式可简化为:

式中,A 为系数矩阵; x 为待求参数; b 为观测值,通常 b 不可避免地会带有一定的误差δ,即观测得到的数据为 b δ,满足‖ b - b δ‖≤δ(‖·‖在本文中若不加特殊说明,为向量2-范数)。由于式(1)中即使 A -1存在,也未必连续,造成观测方程的求解很不稳定。此时,存在最小二乘意义下的解,即残差范数目标函数:
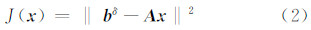
由此得观测方程的最小二乘解为:
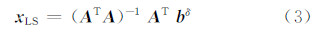
如果观测方程是一个不适定的病态问题,则系数矩阵 A 的奇异值单调递减地趋于0,使得很小的观测误差导致待求参数较大的误差,因此,最小二乘法不能获得满意的结果。一个解决该问题的有效途径是,在式(2)中添加一个对解 x 进行约束的正则化项Ω( x ):
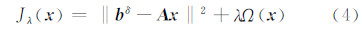
式中,λ为正则化参数。正则化项Ω( x )的选择很多,常见的有2-范数、最大熵、全变差等[1, 10]。令Ω( x )=‖ Rx ‖2( R 为正则化矩阵),式(4)则为Tikhonov正则化,其解为[1]:
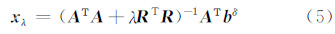
利用矩阵对( A ,R )的广义奇异值进行分解[2],可得:
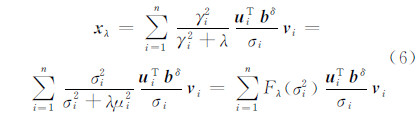
式中,σi和μi分别为算子 A和R 奇异值分解后得到的奇异值;γi=σi/μi;(γi,u i,v i)为矩阵对( A ,R )对应的广义奇异值系统;Fλ(σ2i) 称为Tikhonov正则化的滤波函数:
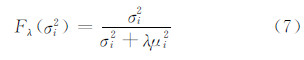
由式(4)和式(5)可知,当令 Ω( x )=‖ Rx ‖2,正则化矩阵 R能够对解x 施加光滑约束,还能改善矩阵 A ΤA 的条件数,因此,R 的选择对Tikhonov正则化的效果有很大影响。令 R = I 是一个选择,此时,式(5)为标准Tikhonov正则化。由Ω( x )=‖ Rx ‖2可知,正则化矩阵 R = I 约束了解 x 的范数,从滤波的角度讲,R = I 等价于限制了观测值 b δ中的所有频率分量,因此,标准Tikhonov正则化方法得到的解过于平滑,而更优化的 R 应该仅约束 b δ中的高频分量(对应系数矩阵 A 中的小奇异值),而使低频分量尽量不变。因此,R 还有其他更好的选择,如一阶导数矩阵(对应梯度算子)、二阶导数矩阵(对应Laplace算子)等[11, 12],其实质是利用一个起高通滤波作用的正则化矩阵来达到仅限制观测值 b δ中高频分量的目的。由于一阶导数矩阵和二阶导数矩阵作为正则化矩阵存在一些不足,且得到的正则化解依然过于光滑[11],本文提出采用Gaussian高通滤波函数作为Tikhonov正则化的正则化矩阵,其具体形式为:

采用这种形式的Gaussian滤波函数,是因为其与标准Tikhonov滤波函数( R = I )存在很强的联系。函数eσ2i/λ的泰勒展开式为:
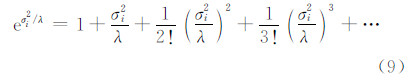
由于 R =e-σi2/λ I 可视为高通滤波函数,则其对应的低通滤波函数为 I - R 。利用式(9)的前两项可近似得:
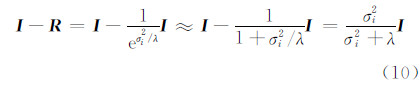
可见,标准Tikhonov低通滤波函数是Gaussian低通滤波函数的近似。由此,结合Gaussian高通滤波函数,可得本文改进的Tikhonov-Gaussian滤波函数为:
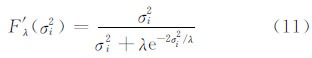
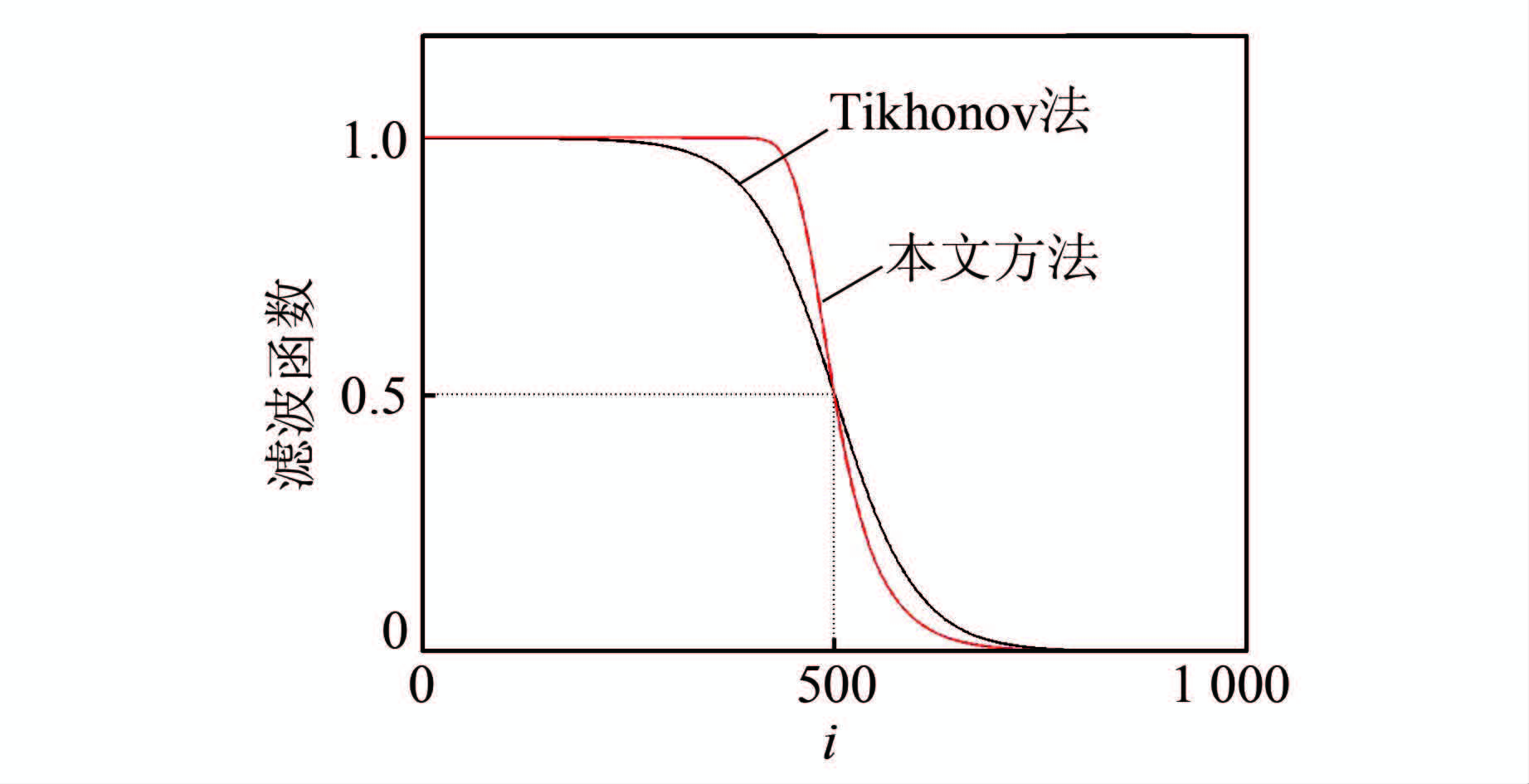
设 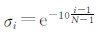 (i=1,2,…,N,N=1 000),则Tikhonov滤波函数Fλ(σi2)和本文提出 的Tikhonov-Gaussian滤波函数F′ λ(σi2)的对比如图 1所示,滤波函数所形成的低通滤波器的截止奇异值位置为500(滤波函数的值降为0.5)。由图 1的比对可知,Tikhonov-Gaussian滤波函数形成的低通滤波器其过渡带明显窄于(或称下降陡度明显大于)Tikhonov滤波函数,而Tikhonov滤波函数相对过于平滑。因此,从低通滤波器的滤波特性角度来讲,Tikhonov-Gaussian的滤波函数明显优于Tikhonov正则化法的滤波函数。
(i=1,2,…,N,N=1 000),则Tikhonov滤波函数Fλ(σi2)和本文提出 的Tikhonov-Gaussian滤波函数F′ λ(σi2)的对比如图 1所示,滤波函数所形成的低通滤波器的截止奇异值位置为500(滤波函数的值降为0.5)。由图 1的比对可知,Tikhonov-Gaussian滤波函数形成的低通滤波器其过渡带明显窄于(或称下降陡度明显大于)Tikhonov滤波函数,而Tikhonov滤波函数相对过于平滑。因此,从低通滤波器的滤波特性角度来讲,Tikhonov-Gaussian的滤波函数明显优于Tikhonov正则化法的滤波函数。
|
| 图 1 Tikhonov法和本文方法滤波函数特性的对比 Fig. 1 Comparison of Characteristic Filter Functions for Tikhonov Method and Our Proposed Method |
正则化参数的选择是除正则化矩阵的选择之外另外一个非常重要的问题。正则化参数的选取依据是否需要预先估计原始数据的噪声水平而分为后验和先验两类策略[1, 13]。Morozov偏差原理[14]是典型的后验策略,该原理易于分析收敛性; L曲线准则[15]和广义交叉校验准则[16]是最常用的两种先验策略。实际应用中,观测值的噪声水平一般是难以预先估计的,因此,一般选择先验策略。
L曲线准则是指以对数尺度来描述 ‖ Rx λ‖,‖Ax λ- b δ‖ ,其关键是定义L曲线的隅角。文献[15]建议定义L曲线的隅角为 最大曲率,但要稳定地计算曲率不是一个简单的过程。文献[17]提出并证明了一种极小化准则,即通过求解函数:
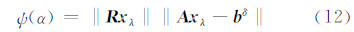
的极小值来达到求解L曲线隅角的目的,并在工程应用中得到使用[18, 19]。本文也采用这种较实用的方法。
3 模型重力数据向下延拓对比实验采用文献[19, 20]中都使用过的双球体重力模型来进行重力数据的向下延拓仿真对比实验。两个球体的参数相同:剩余密度Δσ=1.0 t/m3,半径r=0.5 km,中心埋深为1.8 km,球心x的坐标分别为10 km和15 km,球心y的坐标为12.5 km,z坐标向下为正,线数M和每线点数N同为512,点距Δx和线距Δy都为50 m。
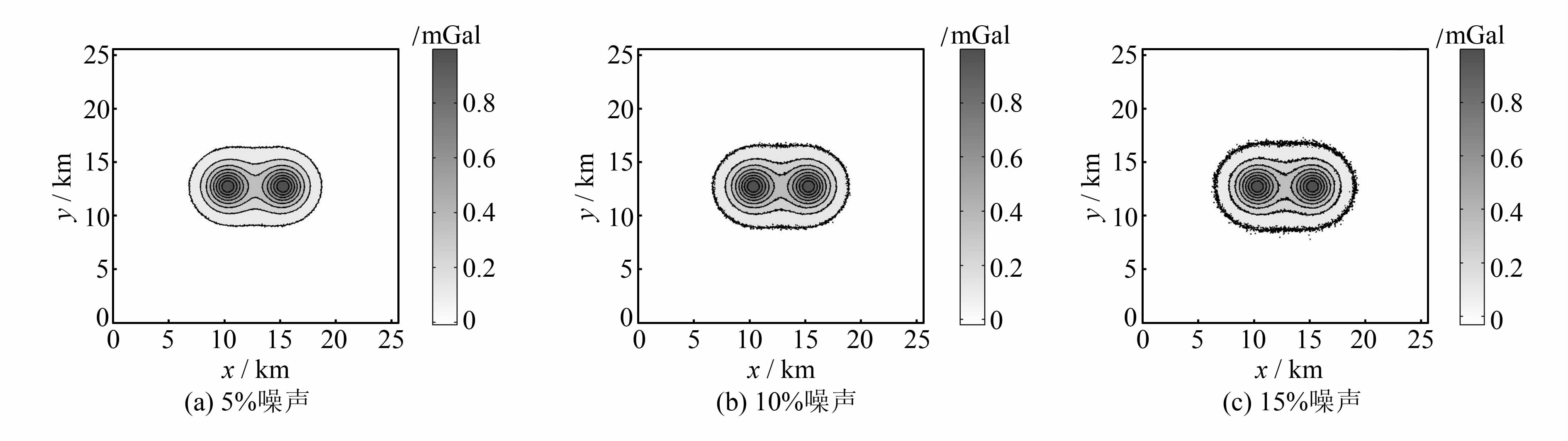
实验中,以h=0 m平面处的重力数据为观测数据,并分别加入零均值、均方差为该高度理论重力异常绝对均值5%(0.002 9 mGal)、10%(0.005 8 mGal)和15%(0.008 8 mGal)的高斯白噪声以模拟实际情况,其结果如图 2所示。分别用Tikhonov法和本文提出的改进方法将加噪数据向下延拓1 000 m(20倍点距),并用得到的延拓值 x λ 与1 000 m深度处的真实重力异常值 x t 采用均方误差(root mean square error,RMSE)和相对误差(relative error,RE)来计算、对比向下延拓误差,其结果见表 1。
| 5%噪声 | 10%噪声 | 15%噪声 | ||||
| Tikhonov法 | 本文方法 | Tikhonov法 | 本文方法 | Tikhonov法 | 本文方法 | |
| 正则化参数 | 0.000 10 | 0.000 14 | 0.000 37 | 0.000 23 | 0.000 89 | 0.000 37 |
| RMSE/mGal | 0.022 0 | 0.019 6 | 0.032 2 | 0.024 7 | 0.042 6 | 0.029 4 |
| RE/% | 5.86 | 4.12 | 9.37 | 4.92 | 12.85 | 5.94 |
|
| 图 2 加噪重力异常等值线图 Fig. 2 Contours of the Gravity Anomaly Data with Noise |
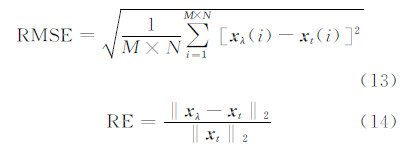
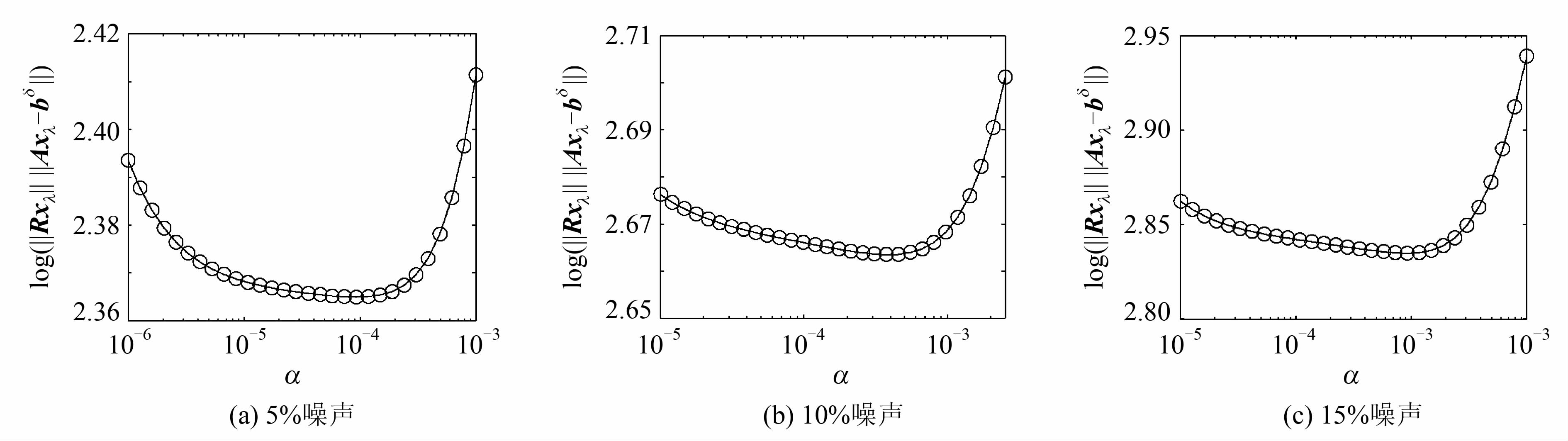
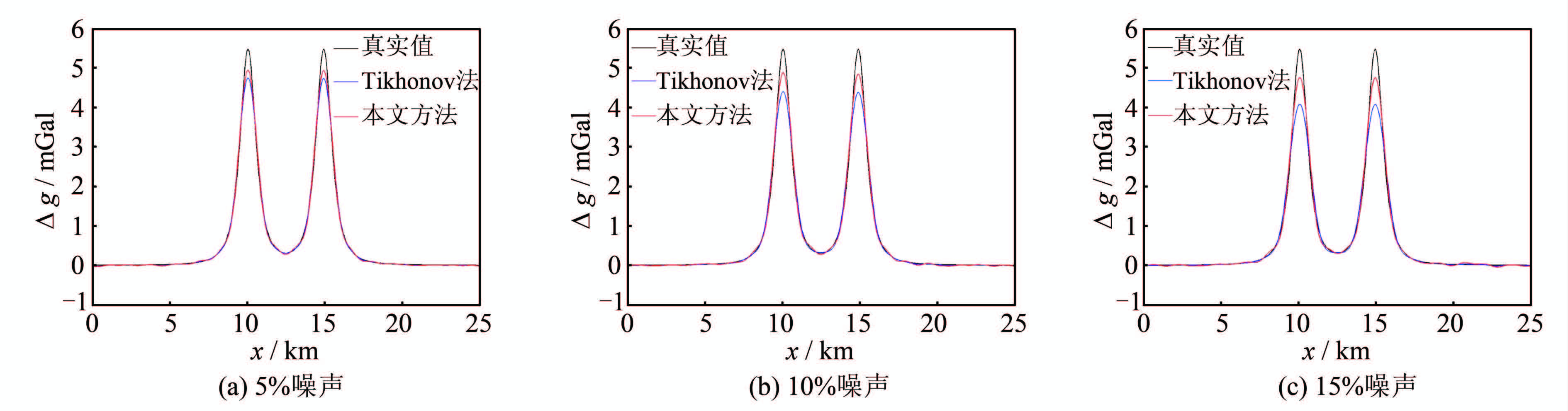
图 3和图 4分别是两种方法采用式(12)求最优正则化参数的辅助曲线图。图 5显示了延拓结果在主剖面的对比图。由表 1和图 4可知:① 各种噪声条件下,本文方法的下延误差都小于Tikhonov法,尤其是相关性误差改善明显;② 伴随所添加的噪声从5%增大到10%和15%,本文方法的下延相关性误差从4.12%增大到4.92%和5.94%,而Tikhonov法的下延相关性误差从5.86%增大到9.37%和12.85%,可见,本文改进方法的鲁棒性更强。
|
| 图 3 Tikhonov法求正则化参数的辅助曲线(式(12)) Fig. 3 Auxiliary Curves for the Calculation of the Regularization Parameters of Tikhonov Method (Eq.(12)) |
|
| 图 4 本文改进方法求正则化参数的辅助曲线(式(12)) Fig. 4 Auxiliary Curves for the Calculation of the Regularization Parameters of Our Proposed Method (Eq.(12)) |
|
| 图 5 各误差条件下两种方法的延拓结果比较(仅图示主剖面) Fig. 5 Comparison of Downward Continuation Results for the Two Methods in Main Profile |
Tikhonov正则化方法是解决病态问题的常用方法,其中,正则化项的引入可以看作是包含了问题的先验信息,能改善问题的病态性。通过选取不同的正则化矩阵可以改变正则化项所包含的先验信息。本文利用Gaussian滤波函数和Tikhonov滤波函数的联系,选用Gaussian滤波函数来构造正则化矩阵,最终使Tikhonov正则化滤波函数的低通滤波特性明显增强。
基于球体模型重力数据向下延拓的对比仿真实验表明,结合正则化矩阵为Gaussian滤波函数的正则化方法,相对于标准形式的Tikhonov正则化方法,下延结果精度更高,且方法的抗噪能力更强。
| [1] | Wang Yanfei. Computational Methods for Inverse Problems and Their Applications[M]. Beijing: Higher Education Press, 2007(王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007) |
| [2] | Hansen R O.Rank-Deficient and Discrete Ill-posed Problems[M]. Philadelphia: Siam,1998 |
| [3] | Tikhonov A N, Arsenin N Y. Solutions of Ill-posed Problems[M]. New York: Wiley, 1977 |
| [4] | Xu P L. Truncated SVD Methods for Discrete Linear Ill-posed Problems[J]. Geophysical Journal International, 1998, 135(2): 505-514 |
| [5] | Kelley C T.Iterative Methods for Linear and Nonlinear Equations[M]. Philadelphia: Siam,1995 |
| [6] | Kirsch A.An Introduction to the Mathematical Theory of Inverse Problems[M]. New York: Springer, 2011 |
| [7] | Gu Yongwei, Gui Qingming, Bian Shaofeng, et al. Comparison Between Tikhonov Regularization and Truncated SVD in Geophysics[J]. Geomatics and Information Science of Wuhan University, 2005, 30(3): 238-241(顾勇为, 归庆明, 边少锋, 等. 地球物理反问题中两种正则化方法的比较[J]. 武汉大学学报·信息科学版, 2005, 30(3): 238-241) |
| [8] | Wang Zhenjie, Ou Jikun, Liu Lintao. A Method for Resolving Ill-conditioned Problems—Two-Step Solution[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9): 821-824(王振杰, 欧吉坤, 柳林涛. 一种解算病态问题的方法——两步解法[J]. 武汉大学学报·信息科学版, 2005, 30(9): 821-824) |
| [9] | Wu Taiqi, Deng Kailiang, Huang Motao, et al. An Improved Singular Values Decomposition Method for Ill-posed Problem[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 900-903(吴太旗, 邓凯亮, 黄谟涛, 等. 一种改进的不适定问题奇异值分解法[J]. 武汉大学学报·信息科学版, 2011, 36(8): 900-903) |
| [10] | Engl H W, Hanke M, Neubauer A. Regularization of Inverse Problems[M]. Netherlands: Kluwer Academic Publishers, 1996 |
| [11] | Wang Y F, Yang C C, Li X W. Regularizing Kernel-based BRDF Model Inversion Method for Ill-posed Land Surface Parameter Retrieval Using Smoothness Constraint[J]. Journal of Geophysical Research, 2008, 113: D13101 |
| [12] | Jiang Peng, Peng Lihui, Xiao Deyun. Tikhonov Regularization Based on Second Order Derivative Matrix for Electrical Capacitance Tomography Image Reconstruction[J]. Journal of Chemical Industry and Engineering, 2008, 59(2): 405-409(江鹏,彭黎辉,萧德云. 采用二阶导数阵作为正则化的电容成像图像重建算法[J]. 化工学报, 2008, 59(2): 405-409) |
| [13] | Bauer F, Lukas M A. Comparing Parameter Choice Methods for Regularization of Ill-posed Problems[J]. Mathematics and Computers in Simulation, 2011, 81(9): 1 795-1 841 |
| [14] | Morozov V A. Methods for Solving Incorrectly Posed Problems[M]. New York: Springer-Verlag, 1984 |
| [15] | Hansen P C, O'Leary D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM J Sci Comput, 1993, 14(6): 1 487-1 503 |
| [16] | Golub G H, Heath M, Wahba G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223 |
| [17] | Reginska T. A Regularization Parameter in Discrete Ill-posed Problems[J]. SIAM J Sci Comput, 1996, 17(3): 740-749 |
| [18] | Guo Chengbao, Xiao Changhan, Liu Daming. Research on the Continuations of Magnetic Field of Magnetic Object Based on Integral Equation Method and Singlar Value Decomposion[J]. Acta Physica Sinica, 2008, 57(7): 4 182-4 188(郭成豹, 肖昌汉, 刘大明. 基于积分方程法和奇异值分解的磁性目标磁场延拓技术研究[J]. 物理学报, 2008, 57(7): 4 182-4 188) |
| [19] | Zeng Xiaomin, Li Xihai, Su Juan, et al. An Adaptive Iterative Method for Downward Continuation of Potential Field Data from a Horizontal Plane[J]. Geophysics, 2013, 78(4): J43-J52 |
| [20] | Liu Dongjia, Hong Tianqiu, Jia Zhihai, et al. Wave Number Domain Iteration Method for Downward of Potential Fields and Its Convergence[J]. Chinese Journal of Geophysics, 2009, 52(6): 1 599-1 605(刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性[J]. 地球物理学报, 2009, 52(6): 1 599-1 605) |
 2015, Vol. 40
2015, Vol. 40


