文章信息
- 谢建, 朱建军
- XIE Jian, ZHU Jianjun
- 等式约束对病态问题的影响及约束正则化方法
- Influence of Equality Constraints on Ill-conditioned Problems and Constrained Regularization Method
- 武汉大学学报·信息科学版, 2015, 40(10): 1344-1348
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1344-1348
- http://dx.doi.org/10.13203/j.whugis20130764
-
文章历史
- 收稿日期: 2013-12-10

大地测量数据处理中,常出现秩亏和病态等现象。解决秩亏问题的常用方法是增加参数间坐标基准的加权等式约束或参数的加权二次范数最小准则,求出特定基准下的最小范数最小二乘解[1]。解病态问题也是附加参数间的加权二次范数约束,使观测残差和参数范数间达到平衡而获得稳定的正则化解[2]。可见,上述不适定问题都是通过增加约束信息来得到适定的解。这种信息有参数的一次式,即参数间的线性等式约束,也有参数的二次式,即参数的二次范数。
对于秩亏数为 d的无约束平差问题,是附加d个线性无关的等式约束消除秩亏[1]。若秩亏问题本身有s个线性无关的约束,那么只要添加d-s个等式约束[3]。 病态问题的正则化准则是对所有的参数施加二次约束,通过压缩解的长度来减弱最小二乘解的不稳定性。但已有文献对等式约束是否减弱病态性少有研究,侧重于研究含有线性等式约束的病态问题的算法。Sarkar在约束最小二乘解前面乘以一个压缩因子,以减小病态约束问题的方差[4];Jürgen在约束最小二乘解的基础上,将最小二乘解用Sarkar解代替,解的形式和约束最小二乘解相同,但是计算非常复杂[5];钟震利用椭圆约束的方法得到了约束病态问题的有偏估计[6];谢建等用正则化的思想得到了附等式约束病态问题的正则化解,其形式与附加椭圆约束的有偏估计相同[7]。
但是,上述方法是对所有的参数施加二次范数约束,都没有讨论等式约束本身能否消除或者减弱系统的病态性,以及附加等式约束后模型的病态程度与哪些因素有关。本文首先将等式约束的病态问题通过消除部分参数转化为无约束问题,分析无约束问题设计阵的病态性,然后给出了等式约束病态问题求解的方法。
1 等式约束对秩亏问题的影响
经典的测量平差函数模型和随机模型为[8]:
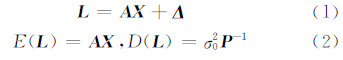
式中,L 、 Δ 分别表示n维观测向量和误差向量; X 为u维参数向量; A 为n×u设计矩阵;σ02为单位权方差; P 为观测权矩阵。根据设计矩阵 A 的性质,可以分为设计阵良态、秩亏和病态三种情况。下面对前两种情况的求解进行分析。
1.1 设计阵 A 是良态矩阵的最小二乘解观测方程(1)相应的误差方程式为[8]:

当设计阵 A 是良态矩阵时,若观测误差服从正态分布,在最小二乘准则φmin( V )= VT PV 下,不需增加额外的信息,可以直接得到唯一且稳定的最小二乘解[8]:

式中,N = A TPA ,w = ATPL ,分别表示法方程矩阵和右端项。
1.2 设计阵 A 秩亏时的自由网平差解
当平差系统缺乏必要的基准条件时,设计阵的秩小于待估参数的个数,即R( A )=t<u。在最小二乘准则下,法方程矩阵求逆不唯一,具有无穷多组解。一般是对参数附加约束信息,得到在某种参考基准或准则下的最优解。一般附加如下s个(s=u-t)等式约束条件[1]:

式中,S是法矩阵N 的s个零特征值所对应的线性无关的特征向量所构成的矩阵; P x称为基准权,反映了不同的基准约束。在最小二乘准则下,可以得到秩亏自由网平差的解为[1]:
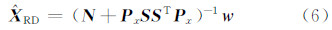
等式约束条件(5)给平差问题提供了必要的基准条件,从而得到了该基准约束下的最小二乘解,但添加的约束条件的个数应等于或大于秩亏数才能得到唯一的解[3]。
2 等式约束对病态问题的影响当设计阵 A 良态时,它的列向量间线性无关;秩亏时,它的列向量间存在线性相关性,若秩亏数为s,那么其中的s列向量可以表示成其他各列的线性组合。而病态矩阵是介于良态矩阵和秩亏矩阵之间的一种,它的列向量间存在近似的线性相关性,线性模型在最小二乘准则下,病态性与复共线性是等价的[9]。方程的病态会引起最小二乘解的不稳定性,一般是对解向量的范数进行限定,使参数估值的长度处于一定的范围。常用的求解病态问题的方法是附加参数的最小范数条件,构成Tikhonov正则化准则[2]:
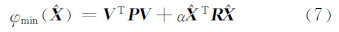
对式(7)求极小,得到相应的正则化解为:
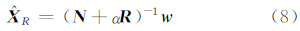
可以证明,对于病态法方程矩阵,附加适当的对角矩阵,可以显著降低法方程的病态,得到的正则化解是最小二乘解的压缩有偏估计[1, 10]。无约束情况下,病态问题最小二乘解的长度不受限制,使解对误差扰动很敏感。增加解的范数约束(7)可以改善法方程矩阵的性质,得到均方误差意义下更优的解。这说明病态问题中对所有参数施加二次约束是可以减弱或消除法方程的病态性的。§1.2的分析表明,附加等式约束能消除秩亏,下面分析给病态问题增加参数间的一次等式约束条件能否减弱方程的病态性。
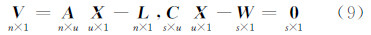
这里假设约束条件相容且线性无关,若约束关系中不包含某些参数,则可以使约束矩阵中对应于该参数的列为零向量。常用的解模型(9)的方法是采用准则函数(7),得到如下形式的等式约束正则化解[6, 7]:
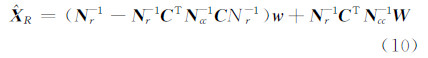
式中,N r= N +α R ; N cc= CN -1r C T。可见上述方法是对所有参数进行正则化,没有考虑等式约束本身能否减弱或消除病态性。为了便于分析,先将等式约束平差模型转变成一个无约束平差模型[11]。可以在s个约束条件中消去其中任意s个参数,剩下的t=u-s个参数可由这s个参数表达。式(9)中对参数分类后的等价形式为[11]:

式中,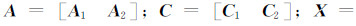
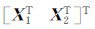 ,由式(12)可以得到:
,由式(12)可以得到:
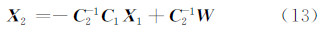
代入式(11),即得:
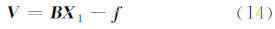
式中,B = A 1- A 2 C -12 C 1; f = L - A 2 C -12 W 。 新的设计矩阵 B是原有的病态设计阵A和良态约束阵C 的子矩阵的线性组合,它的性质由原设计阵的病态性、参数的约束个数及约束的形式共同决定,有可能呈病态或良态。对每个不同的实际测量问题,等式约束是由先验信息或者经验知识获得,随问题的不同而不同。在对参数分组时,没有特定的标准,因此系数阵 B 的病态性难以从数学上给出直接的证明过程。也就是说,在 A 1、 A 2、 C 1、 C 2均不定的情况下,难以直接计算 B 矩阵的行列式、条件数、特征值或条件指标等反映病态程度的指标。这里可以用两个极端的例子来说明等式约束对法方程矩阵病态性的影响。
1) 当有s=u-1个参数间的约束条件,即转换后的无约束平差模型只有t=1个参数时,由 B 的表达式易知,B 是一个n维向量,式(14)相当于仅含一个参数的平差模型,它的最小二乘解为:
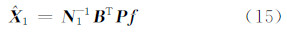
式中,N 1= B T PB 是一常数,总可以求得稳定的凯利逆,从而这一约束消除了法方程的病态性。
由式(15)得到 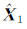 的估值以后,代入式(13)可以得到其他参数的估值。
的估值以后,代入式(13)可以得到其他参数的估值。
2) 当附加如下的约束条件时:

式中,d 表示s×1维常数向量。这种情况实际上是已知某部分参数的值,求剩余t个参数的估值。容易知道,C 1是一个s×t的全零矩阵。此时,模型(11)、(12)等价于:

即 B = A 1,B 的性质完全由 A 1所决定。设矩阵 A 用列向量表示为:
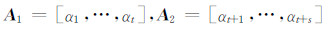
式中,αi(i=1,2,…,t+s)为n维列向量。若 A 病态,则一定存在不全为0的常数ki(i=1,2,…,t+s),使得:
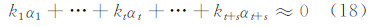
成立。那么 A 1是否病态又分为如下几种情况:
1) 存在不全为0的常数ki(i=1,2,…,t),使得k1α1+…+ktαt≈0,当且仅当kt+1=kt+2=…=kt+s=0时,才有kt+1αt+1+…+kt+sαt+s=0成立。也就是说,矩阵的复共线性仅存在于前面t列,后面的s列线性无关,A 1的病态性和 A 完全一致,即cond( A 1)=cond( A )。即附加式(17)所示的约束条件完全不能减弱新的误差方程(14)的病态性,需要求正则化解。
2) 跟情形1)完全相反,矩阵的复共线性仅存在于后面s列,而前面t列线性无关,那么 A 1是一个良态矩阵,设条件数为M。附加式(17)这一约束条件后,可以直接按照普通最小二乘法求解。
3) 除去情形1)和情形2)以外的情况,这时,不仅子矩阵 A 1的列向量间存在复共线性,子矩阵 A 2的列向量间也存在复共线性,或者 A 1和 A 2的列向量间互相存在近似线性相关关系。由于情形1)、2)分别是两种极端情况,那么 A 1的病态性处于两种情形之间,即M
从以上两例可以看出,线性消元后,新模型(14)的系数阵是否病态不仅与原设计矩阵 A 本身的性质有关,而且与约束矩阵有关。随着以上两个因素发生变化,新模型设计阵 B 可能是良态或病态,且病态程度不会比原设计阵 A 的性质更差,满足如下关系: 1≤cond( B )≤cond( A )。
3 等式约束病态问题的正则化解对于附有等式约束的病态模型,可以根据式 (12)先选取任意s个参数,将其表达成另外t个参数的线性组合,然后组成形如式(14)的无约束误差方程式。为了确定新的误差方程设计阵是否病态,可以采用病态问题诊断的一系列方法,如行列式法、方差因子扩大法和条件数法[12]、条件指标-方差分解比法[13]、 特征分析法[14]等。
这里采用文献[12]所给出的条件数法来判断新的设计阵是否病态。当条件数小于100时,可以认为没有病态;当条件数处于100~1 000之间,认为具有中等病态性;当条件数大于1 000时,认为病态性严重。对于没有病态性的设计阵,可以直接运用最小二乘法求解t个已选参数,代入式(13)求消去的参数。对于具有病态设计阵的方程(14),采用Tikhonov正则化方法求解:
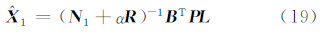
其中,N 1= B T PB 为转换后的法矩阵; R 为描述函数光滑性的正则化矩阵,本文取 R 为单位阵,这里只对剩余参数进行正则化;α为正则化因子,常用的正则化因子选取方法有岭迹法[1]、GCV(generalized cross validation)法[15]、L曲线法[16, 17]、Helmert方差分量估计法[18]、均方误差极小法[19]。这里采用均方误差极小化方法确定正则化因子。 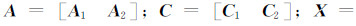 的均方误差为[19]:
的均方误差为[19]:
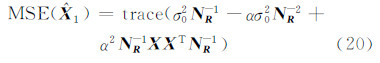
其中,trace(·)表示矩阵的求迹; N R = N 1+α R 。式(20)中含有参数真值 X ,在求解时是未知的。均方误差极小化求解的具体实现过程是:首先计算最小二乘解,将其作为近似真值代入均方误差 表达式(20)中,用最优化方法求均方误差极小时的正则化因子,得到新的正则化估值;然后将新的估值作为真值,用同样的方法求解极小化问题,直到最后两次解的差值小于给定的阈值后停止迭代。
4 算例分析采用文献[17]的算例,在这个算例中,有10个观测值,5个未知数,其真值为 X =[1 1 1 1 1],观测噪声 Δ ~(0,1),由随机发生器生成,观测值由 L = AX + Δ 生成。各观测值等精度,权矩阵为单位阵。系数矩阵 A 如下:

它的条件数为cond( A T A )=1.289 2×105,严重病态。分别附加如下的约束条件,分析不同的约束条件对消除或减弱方程病态性的影响,并计算各种情形下的解:① Xi+Xi+1=2,i=1;② Xi+Xi+1=2,i=1,2; ③ Xi+Xi+1=2,i=1,2,3; ④ Xi+Xi+1=2,i=1,2,3,4。
对4种不同的等式约束条件,其约束个数分别为1、2、3、4个,那么被消去参数的个数与约束的个数相同。消去这些参数后,剩余的参数个数分别为4、3、2、1个,在求均方误差项时,分别求得4种约束情形下剩余参数的均方误差。由于被消去参数的个数不同,所以不能同等地比较各种情形下的均方误差。由于是模拟计算已知真值的大小,可以计算真误差,表 1中真误差的平方和随着约束的增加而显著减小。
| X 1 | X 2 | X 3 | X 4 | X 5 | cond(N 1) |
MSE(
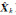 ) ) |
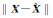 |
|
| 真值 | 1 | 1 | 1 | 1 | 1 | - | 0.000 0 | 0.000 0 |
| 无约束最小二乘解 | -0.418 4 | 13.095 5 | 4.250 2 | 4.843 8 | -4.958 3 | 1.28×10 5 | 320.882 5 | 209.151 8 |
| 无约束正则化解(α=1.43) | 1.523 6 | 0.448 2 | 1.086 8 | 0.784 3 | 1.328 3 | 1.28×10 5 | 0.673 5 | 0.740 5 |
| 约束①(α=1.27) | 1.437 1 | 0.562 9 | 1.114 6 | 0.952 6 | 1.271 9 | 8.51×10 4 | 0.149 9 | 0.471 4 |
| 约束②(α=0) | 1.234 9 | 0.765 1 | 1.234 9 | 1.499 8 | 1.173 3 | 35.285 7 | 0.078 3 | 0.443 6 |
| 约束③(α=0) | 1.121 9 | 0.878 1 | 1.121 9 | 0.878 1 | 1.119 8 | 12.55 | 0.022 2 | 0.073 8 |
| 约束④(α=0) | 1.119 1 | 0.880 9 | 1.119 1 | 0.880 9 | 1.119 1 | 1 | 0.024 8 | 0.070 9 |
从以上算例可以看出,增加约束能减弱或者消除法方程的病态性。随着约束条件的增加,新的平差系统的病态性逐渐减弱,当约束条件增加到2个时,法方程的条件数已经低于100的阈值,病态性完全消除了,此时可以直接采用最小二乘进行平差计算。
5 结 语对于附有等式约束的病态问题,通过消除部分参数的方法将其转变为一个无约束病态问题。在新的观测方程中,用计算实例分析了设计阵的病态性,并指出新的设计阵可能是病态的,也有可能是良态的,取决于原设计矩阵和约束矩阵的性质。它的条件数介于原设计阵的条件数和1之间。利用条件数法来判断新的设计阵的病态程度,对于仍然呈病态的模型,采用Tikhonov正则化方法求解参数,正则化因子由均方误差极小化方法确定。然后利用约束条件式得到剩余参数的估值。数值实验证明本文提出的方法是有效的、可行的。
| [1] | Cui Xizhang. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2001:163-170(崔希璋. 广义测量平差[M]. 武汉:武汉大学出版社,2001:163-170) |
| [2] | Tikhonov A N. Regularization of Ill-posed Problem[J]. Dokl Akad Nauk SSSR, 1963, 151(1) : 49-52 |
| [3] | Xie Jian, Zhu Jianjun. A New Approach to Constrained Rank-deficient Free Network Adjustment[J]. Engineering of Surveying and Mapping, 2009, 18(2):9-11(谢建,朱建军. 约束秩亏网平差的一种新算法[J]. 测绘工程,2009,18(2):9-11) |
| [4] | Sarkar N. A New Estimator Combining the Ridge Regression and the Restricted Least Squares Methods of Estimation[J]. Comm Statist Theory Methods,1992,21(7):1 987-2 000 |
| [5] | Jürgen G. Restricted Ridge Estimation[J]. Statistics & Probabilities Letters, 2003,65(1):57-64 |
| [6] | Zhong Zhen. Study on the Restricted Biased Estimation in the Linear Model[D]. Chongqing: Chongqing University, 2005(钟震. 线性模型中的约束型有偏估计的研究[D]. 重庆:重庆大学, 2005) |
| [7] | Xie Jian, Zhu Jianjun. A Regularized Solution and Statistical Properties in Ill-posed Problems with Equality Constraints[J]. Geomatics and Information Science of Wuhan University, 2013,38(12):1 440-1 444 (谢建,朱建军. 等式约束病态模型的正则化解及其统计性质[J]. 武汉大学学报·信息科学版,2013,38(12):1 440-1 444) |
| [8] | Group of Adjustment Discipline in School of Geodesy and Geomatics of Wuhan University. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press,2003(武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M]. 武汉:武汉大学出版社,2003) |
| [9] | Guo Jianfeng. Diagnosis and Processing of Ill-posedness in Adjustment Model[M]. Zhengzhou: Information Engineering University, 2002(郭建锋. 测量平差系统病态性的诊断与处理[D]. 郑州:信息工程大学,2002) |
| [10] | Zhang Jinhuai. Parameter Estimation of Linear Models and Its Improvement[M]. Changsha: National University of Defense Technology,1992(张金槐. 线性模型参数估计及其改进[M]. 长沙:国防科技大学出版社,1992) |
| [11] | Yu Zongchou. The Uniformity Theory of Estimation of Variance-Covariance Components[J]. Acta Geodaetica et Cartographica Sinica, 1991,20(3):161-171(於宗俦.方差-协方差分量估计的统一理论[J]. 测绘学报,1991,20(3):161-171) |
| [12] | Chen Xiru, Wang Songgui. Modern Regression Analysis[M]. Hefei: Anhui Education Press,1987(陈希孺,王松桂. 近代回归分析[M]. 合肥:安徽教育出版社,1987) |
| [13] | Gui Qingming, Yao Shaowen, Gu Yongwei, et al. A New Method to Diagnose Multicollinearity Based on Condition Index and Variance Decomposition Proportion(CIVDP)[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(3):210-214(归庆明,姚绍文,顾勇为,等. 诊断复共线性的条件指标-方差分解比法[J]. 测绘学报,2006,35(3):210-214) |
| [14] | Golub G H, Heath M, Wahba G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter[J]. Techno Metrics, 1979,21(2):215-223 |
| [15] | Han Songhui, Du Lan, Gui Qingming, et al. Characteristics Analysis Approach for Multicollinearity Diagnosis and Its Applications in Orbit Determination of GEO Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1):19-26(韩松辉,杜兰,归庆明,等. 诊断复共线性的特征分析法及其在GEO定轨中的应用[J]. 测绘学报,2013, 42(1):19-26) |
| [16] | Hansen P C. Analysis of Discrete Ill-posed Problems by Means of the L-curve[J]. SIAM Review, 1992, 34(4): 561-580 |
| [17] | Wang Zhenjie. Determining the Ridge Parameter in a Ridge Estimation Using L-curve Method[J]. Geomatics and Information Science of Wuhan University, 2004,29(3):235-238(王振杰. 用L-曲线法确定岭估计中的岭参数[J]. 武汉大学学报·信息科学版,2004,29(3):235-238) |
| [18] | Zhu Jianjun, Tian Yumiao, Tao Xiaojing, et al. United Expression and Solution of Adjustment Criteria with Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(1):8-13(朱建军,田玉淼,陶肖静, 等. 带准则参数的平差准则及其统一与解算[J]. 测绘学报,2012,41(1):8-13) |
| [19] | Xu Peiliang. Determination of Surface Gravity Anomalies Using Gradiometric Observables[J]. Geophys J Int , 1992,110(2): 321-332 |
 2015, Vol. 40
2015, Vol. 40


