文章信息
- 潘国荣, 郭巍, 周跃寅
- PAN Guorong, GUO Wei, ZHOU Yueyin
- 一种基于先验误差分解定权的精密测量拟合算法
- A Precise Measurement Fitting Algorithm Based on Priori Error Decomposition Weighting
- 武汉大学学报·信息科学版, 2015, 40(10): 1339-1343
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1339-1343
- http://dx.doi.org/10.13203/j.whugis20130768
-
文章历史
- 收稿日期: 2013-12-11

随着工业生产对构件制造精度和尺寸工艺要求的提高,高精度的工业测量拟合算法成为研究的热点[1, 2, 3]。文献[4]将直线拟合应用于角点检测,文献[5]将空间直线拟合应用于卫星天线的精密校准,文献[6, 7]分别基于粗差剔除理论和空间数据分布特性研究了点云的空间平面拟合,文献[8, 9]基于平差理论研究了空间圆、球精密拟合算法,文献[10]基于移动最小二乘理论研究了曲线和曲面拟合,文献[11]研究了曲线快速拟合,提出了肩点检测(shoulder point detection,SPD)算法。
全站仪、激光跟踪仪等测量仪器的应用为大尺寸构件的测量提供了高效手段,然而由于极坐标测量系统往往具有不同量级的测角精度和测距精度,加之测量仪器与测点的相对位置不同,从而导致各测点测量数据不同方向上误差分量的不同。一般工业拟合计算是等权处理各点位数据[12],忽略了测量误差对拟合结果的影响,也未考虑测点处不同方向误差分量的差异性。本文提出的算法依据待拟合工件的形状和姿态,考虑了仪器和测点的相对空间关系,将测量误差在测点处分解为多个分量,再根据仪器测角和测距的先验误差重新评定测点各误差分量的大小,并依此作为拟合计算的定权依据。
1 误差分量影响分析 1.1 相关定义径向误差:圆、球形工件在测点处指向圆心或球心方向的误差分向量,记为 ER,直接影响圆、球的半径拟合结果。
切向误差:与圆、球形工件在测点处切线或切面方向的误差分量,记为ET,影响圆、球的半径。相比径向误差,影响量较小。
垂向误差:在测点处垂直于直线、平面或圆面的误差分向量,记为EV,该误差对工件形状和姿态的拟合结果影响较大。
平向误差:在测点处平行于直线、平面或圆面的误差分向量,记为EH,该误差对线、面形工件姿态的拟合结果无影响。对于空间圆,该误差分量为切向误差和向心误差的矢量和,对圆的半径拟合有影响。
记测量仪器的测角误差为ζ,测距常数误差为a,测距系数误差为k,记仪器中心位置为P0(X0,Y0,Z0),记某测点的测量结果为Pi(Xi,Yi,Zi)(i∈N)。
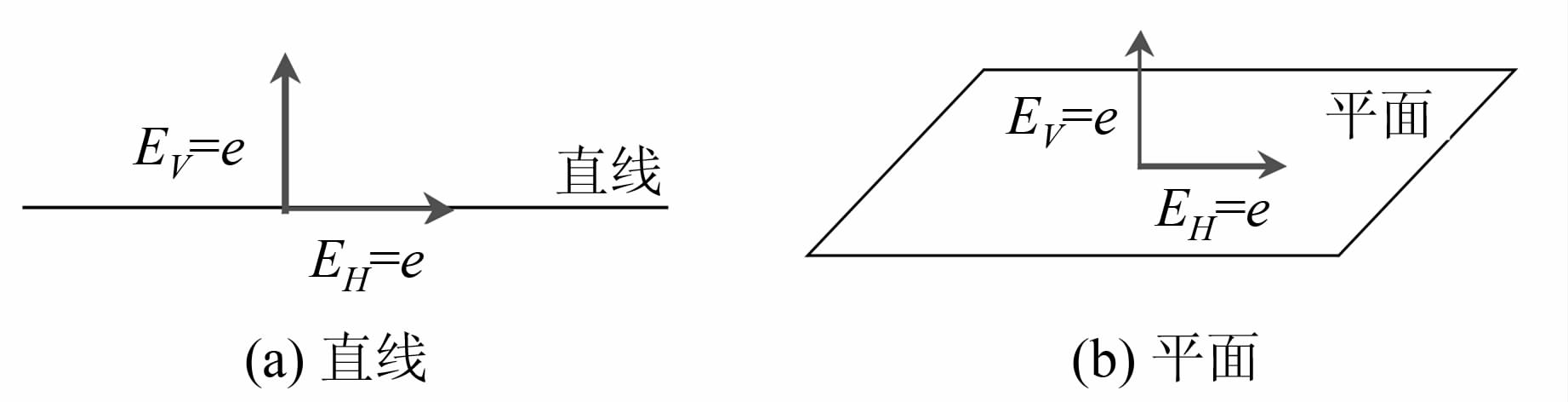
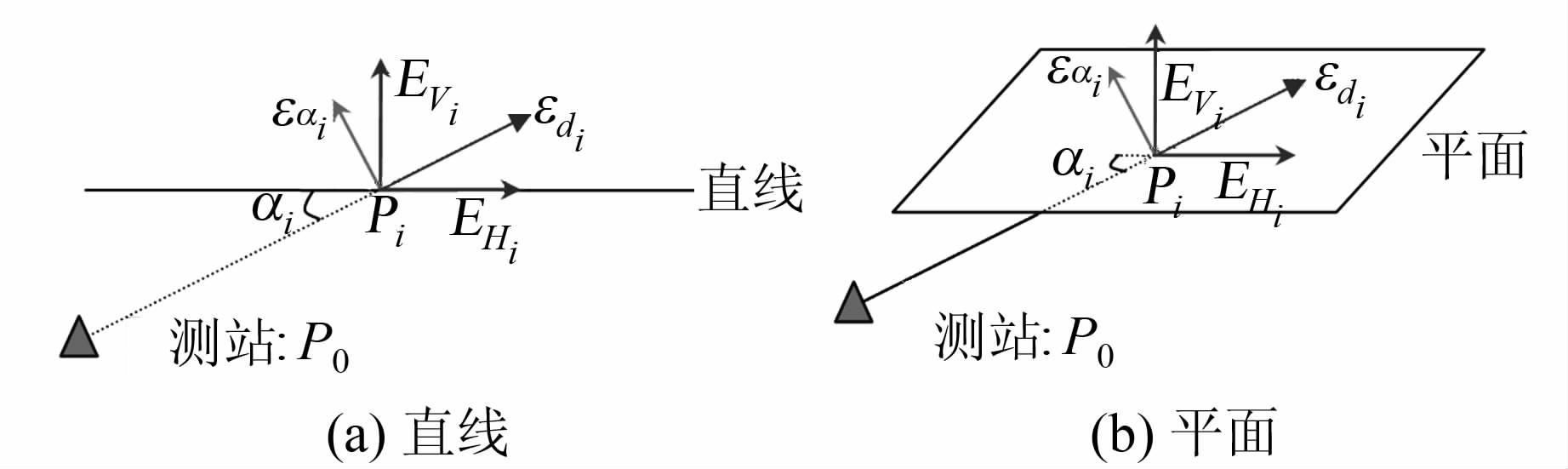
1.2 空间直线与平面测点的误差分解对于直线和平面来说,等量的垂向误差和平向误差对其拟合精度的影响差异如图 1所示。可见,对于直线和平面,平向误差不影响其空间形状和姿态,垂向误差则影响了空间直线和平面的拟合结果。因此,等量的垂向误差和平向误差e对直线和平面的影响比为e∶0。考虑仪器位置,关于直线和平面测点处的误差分解如图 2所示。
|
| 图 1 垂向误差与平向误差对线/面拟合的影响 Fig. 1 Effect of Vertical Error and Horizontal Error on Line/Plane Fitting |
|
| 图 2 面测点误差分解示意图 Fig. 2 Point Error Decomposition Schematic Diagram for Line/Plane |
下面考虑测站位置和工件姿态,分析某测距、测角精度下线、面上不同位置测点的垂向误差和平向误差,并依此作为定权依据。根据空间几何原理[13],易得其函数关系为:
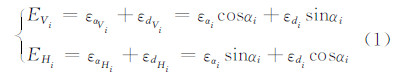
其中,εαi=tanζ·Disti,εdi=a+k·Disti,Disti为测点Pi到测站P0的距离;a为测距常数误差;k为测距系数误差。对于直线和平面,只有垂向误差分量影响其拟合形状和姿态,在此设单位权中误差为1,则其测点拟合定权为:
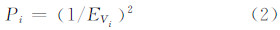
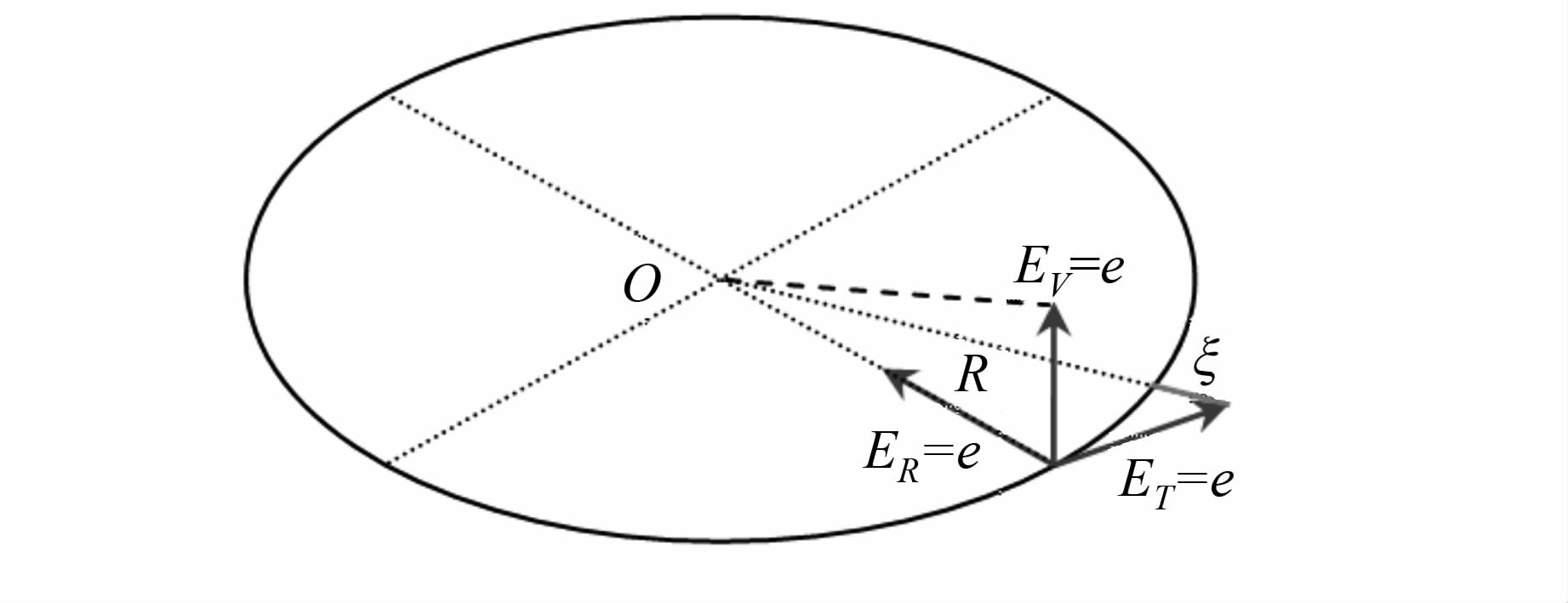
空间圆拟合可看为空间平面拟合和平面圆拟合的组成,等量的径向误差、切向误差和垂向误差对空间圆参数的拟合影响差异如图 3所示。
|
| 图 3 径向误差、切向误差和垂向误差 对空间圆拟合的影响 Fig. 3 Effect of Radial Error, Tangential Error and Vertical Error on Spatial Circle Fitting |
假设在三个方向上都存在大小为 e的误差分向量,由空间几何原理可知,3个分量对圆半径的影响比为 e∶ξ∶η,对圆面姿态的影响为0∶0∶γ,其中
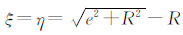 ,R为待拟合圆的半径真值,γ=arctan(e/R)。考虑仪器位置,圆测点的误差分解如图 4所示。
,R为待拟合圆的半径真值,γ=arctan(e/R)。考虑仪器位置,圆测点的误差分解如图 4所示。
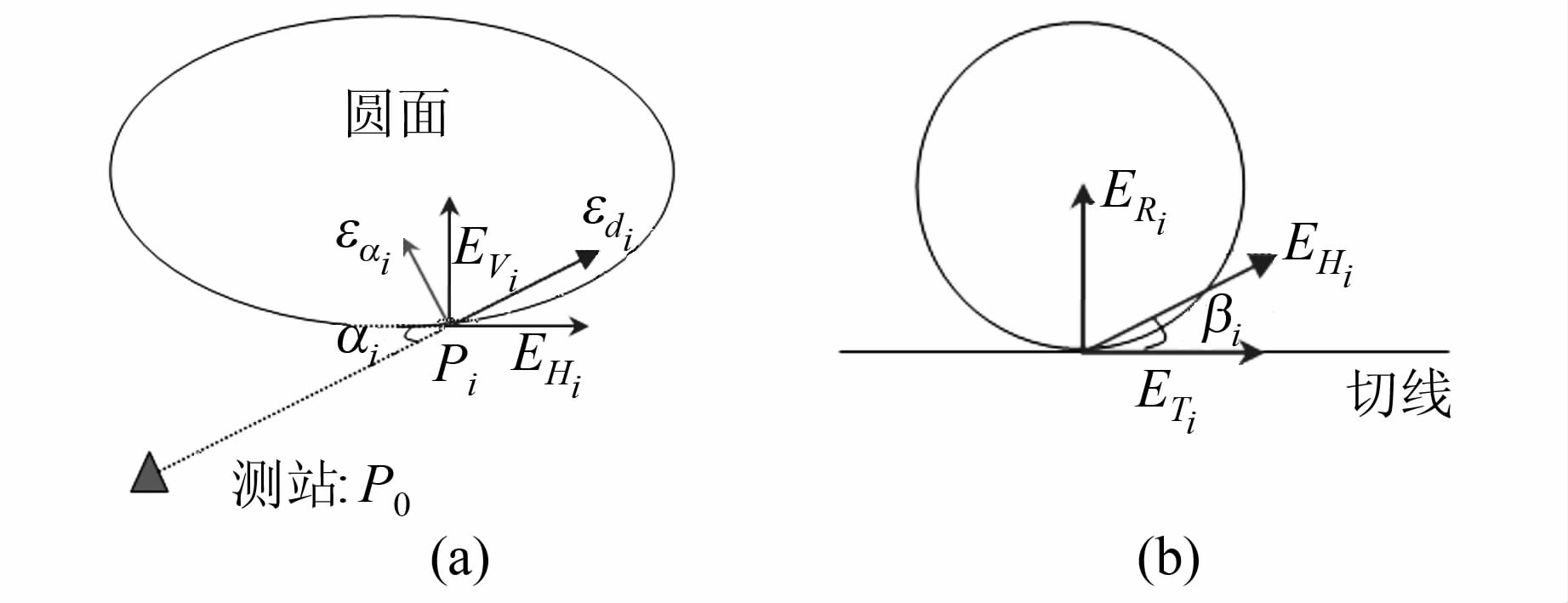
|
| 图 4 空间圆测点误差分解示意图 Fig. 4 Point Error Decomposition Schematic Diagram for Spatial Circle |
将误差先依据圆平面分解成垂向误差分量和平向误差分量,方法与式(1)相同,然后按式(3)将平向误差分解为径向误差分量和切向误差分量:
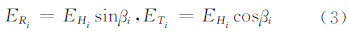
其中,β为平向误差分量与圆上测点切线的夹角。类似的,球面拟合受到径向误差和切向误差的影响,假设在两个方向上都存在大小为e的误差,则其影响比为 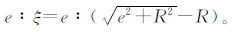 考虑仪器位置,球面测点的误差分解如图 5所示。
考虑仪器位置,球面测点的误差分解如图 5所示。
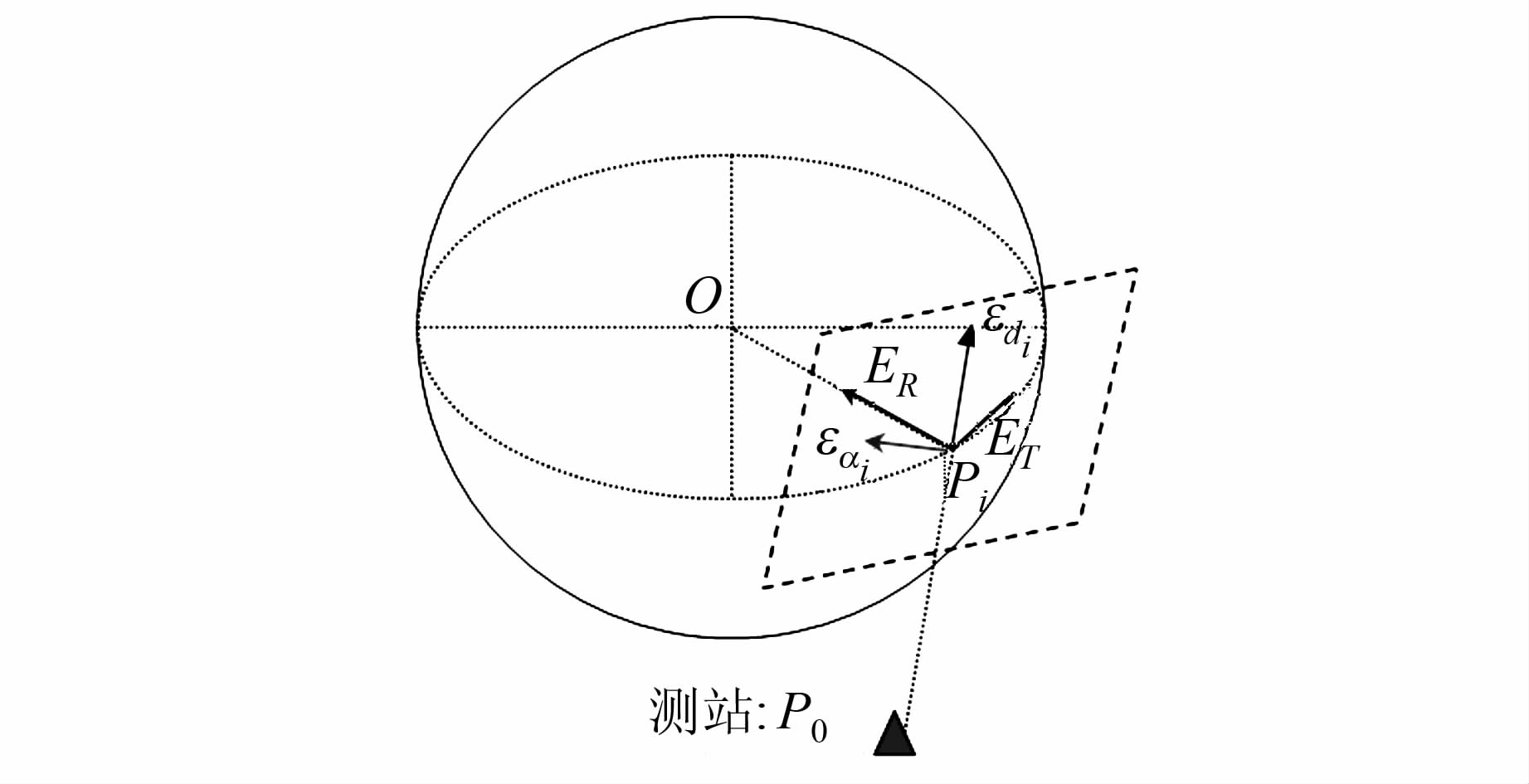
|
| 图 5 球面测点误差分解示意图 Fig. 5 Point Error Decomposition Schematic Diagram for Sphere |
对于球面,在测点处,切平面上的垂向误差分量和平向误差分量即为对该球的径向误差分量和切向误差分量,因此求球面测点的切面是球面测点误差分解的第一步,随后的分解方法与式(1)相同,不再赘述。根据以上分析,本文中对空间圆测点的权值计算方法为:
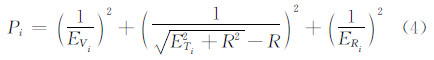
对球面测点的权值计算方法为:
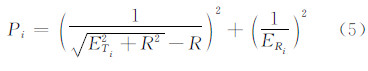
先验误差分解定权拟合算法(priori errors decomposition weighted fitting algorithm,PE-DWF)的基本流程如下:
1) 先按照各测点等权初步拟合空间几何体,以确定各测站-测点连线以及几何体的空间姿态;
2) 考虑仪器的先验测角误差和测距误差,根据§1.2和§1.3中提及的误差分解方法,对各测点误差进行分解,提取出影响构件拟合结果参数的误差分量,以此分量为各测点再次拟合定权;
3) 依据各测点新权值重新进行不等权拟合计算,具体计算过程因拟合体的形状不同而不同。关于线、面、圆和球的误差分解定权方法已在§1.2和§1.3中进行了叙述,而具体拟合计算采用已成熟的算法[2],此处不再赘述。
3 实验与分析
由于现实中很难找到标准的空间直线、平面、圆和球作为设计对比参照,因此本文实验以仿真 为主,即通过数学模拟法获取标准空间直线、平面、圆和球及其表面点,再根据测量仪器的先验误差特性和测站位置对模拟的表面点进行添加误差处理,使其与实际测量数据具有相同的误差分布规律,然后分别用等权拟合和PE-DWF拟合对模拟测点数据进行拟合计算,进而比较分析拟合结果与标准几何体的参数和姿态差异。
生成模拟测点数据的步骤为:① 模拟理论空间线、面、圆、球方程;② 在理论线、面、圆、球上取点,获取理论测点的三维坐标 ;③ 依据测站位置,将理论
;③ 依据测站位置,将理论 转化为理论水平角、竖直角和斜距的原始观测值(
转化为理论水平角、竖直角和斜距的原始观测值( 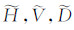 );④ 依据仪器标称的先验测距测角误差为理论(
);④ 依据仪器标称的先验测距测角误差为理论( 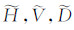 )模拟添加测量误差,得到含误差的(H,V,D);⑤ 再将含误差的(H,V,D)转化为含误差的(X,Y,Z)。
)模拟添加测量误差,得到含误差的(H,V,D);⑤ 再将含误差的(H,V,D)转化为含误差的(X,Y,Z)。
分别针对空间线、面、圆和球,依据测点数据模拟生成方法在典型的测距、测角误差(测角误差1″,测距误差1+1×10-6)下进行100次模拟数据生成和拟合计算实验,并将等权拟合、PE-DWF拟合的结果与标准空间几何体参数进行比较,以分析PE-DWF算法的性能。
1) 空间直线拟合仿真实验
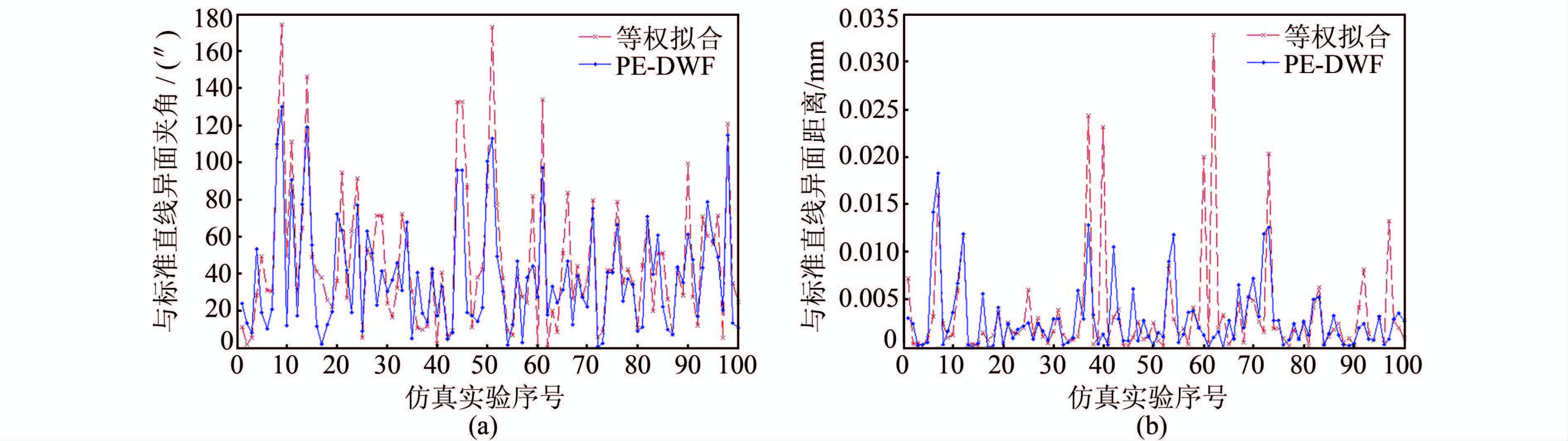
空间直线等权拟合和PE-DWF拟合结果与标准直线的异面夹角和异面距离的比较见图 6。
|
| 图 6 与标准空间直线异面夹角和异面距离的比较 Fig. 6 Comparison of Standard Spatial Line on Intersection Angle and Distance in Different Planes |
由图 6可知,空间直线的PE-DWF拟合与等权拟合相比,异面夹角平均减小16.88%,异面距离平均减小15.61%。
2) 空间平面拟合仿真实验
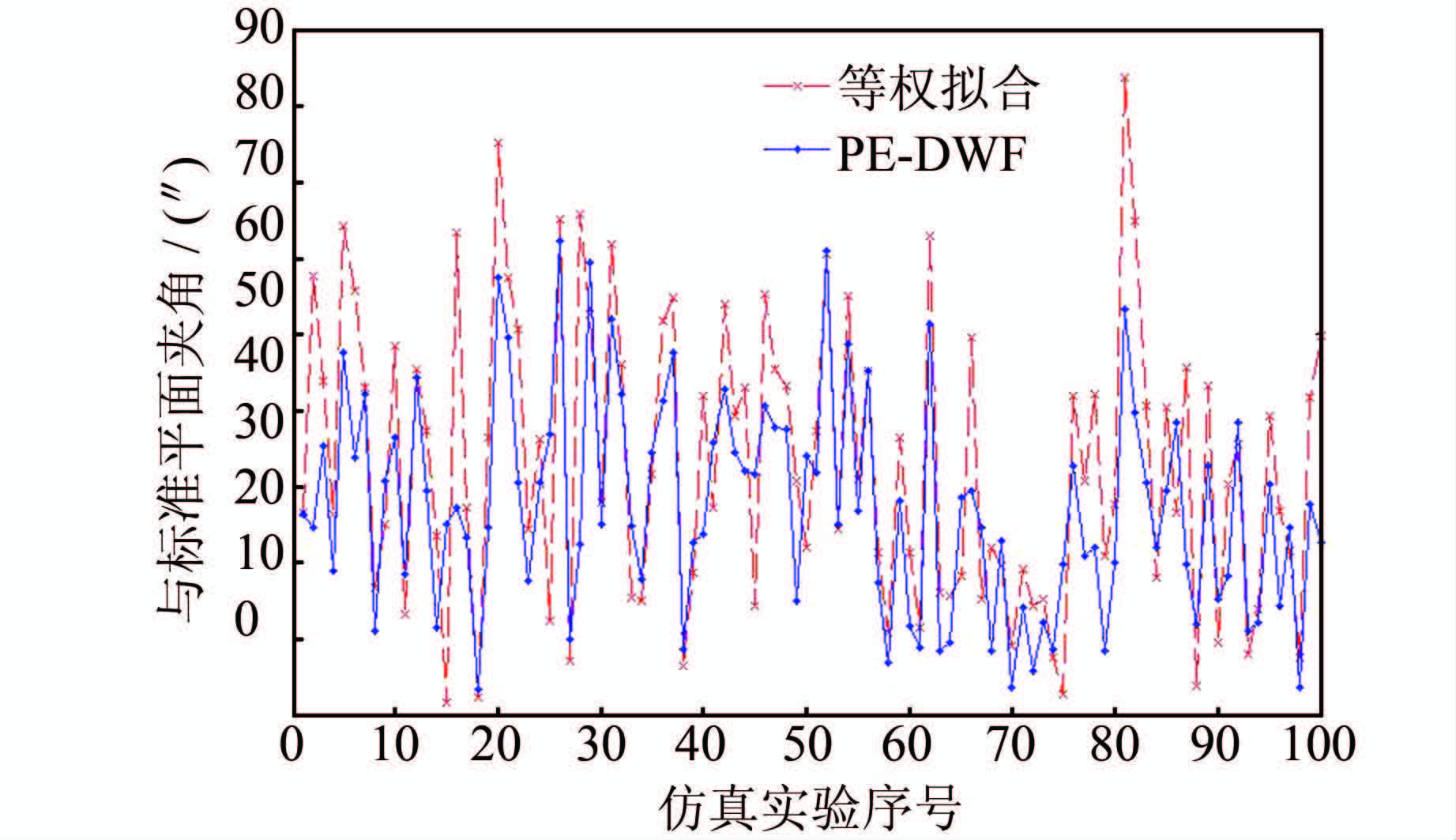
平面等权拟合和PE-DWF拟合结果与标准空间平面夹角的比较如图 7所示。
|
| 图 7 与标准空间平面夹角的比较 Fig. 7 Comparison of Standard Spatial Plane on Intersection Angle |
由图 7可知,空间平面的PE-DWF拟合与等权拟合相比,平面夹角平均减小17.39%。
3) 空间圆拟合仿真实验
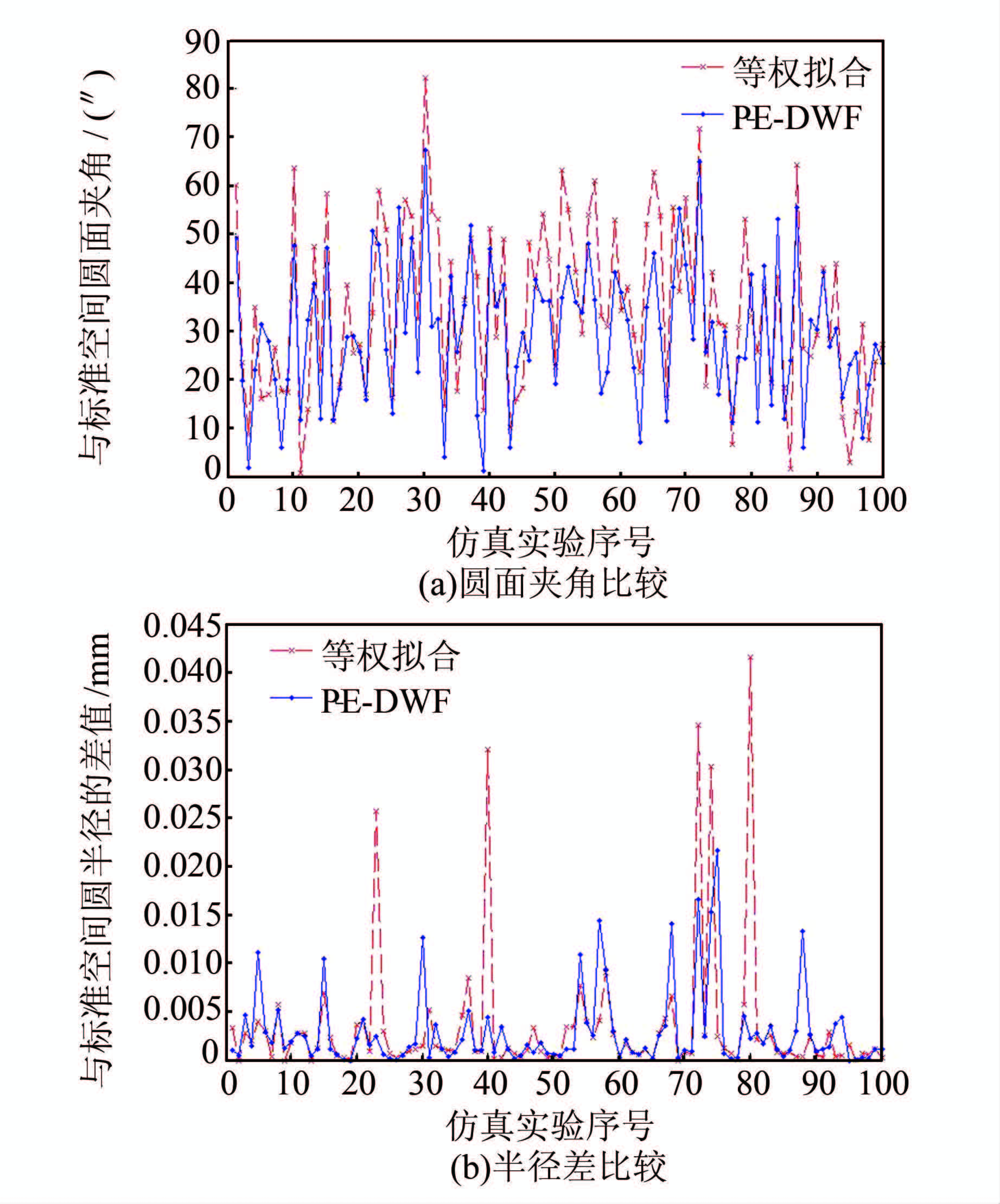
空间圆等权拟合和PE-DWF拟合结果与标准圆的圆面夹角和半径差值的比较如图 8所示。
|
| 图 8 与标准空间圆圆面夹角与半径差的比较 Fig. 8 Comparison of Standard Circle on Intersection Angle and Radius Difference |
由图 8可知,空间圆的PE-DWF拟合与等权拟合相比,圆面夹角平均减小15.60%,圆半径误差平均减少15.17%。
4) 球拟合仿真实验
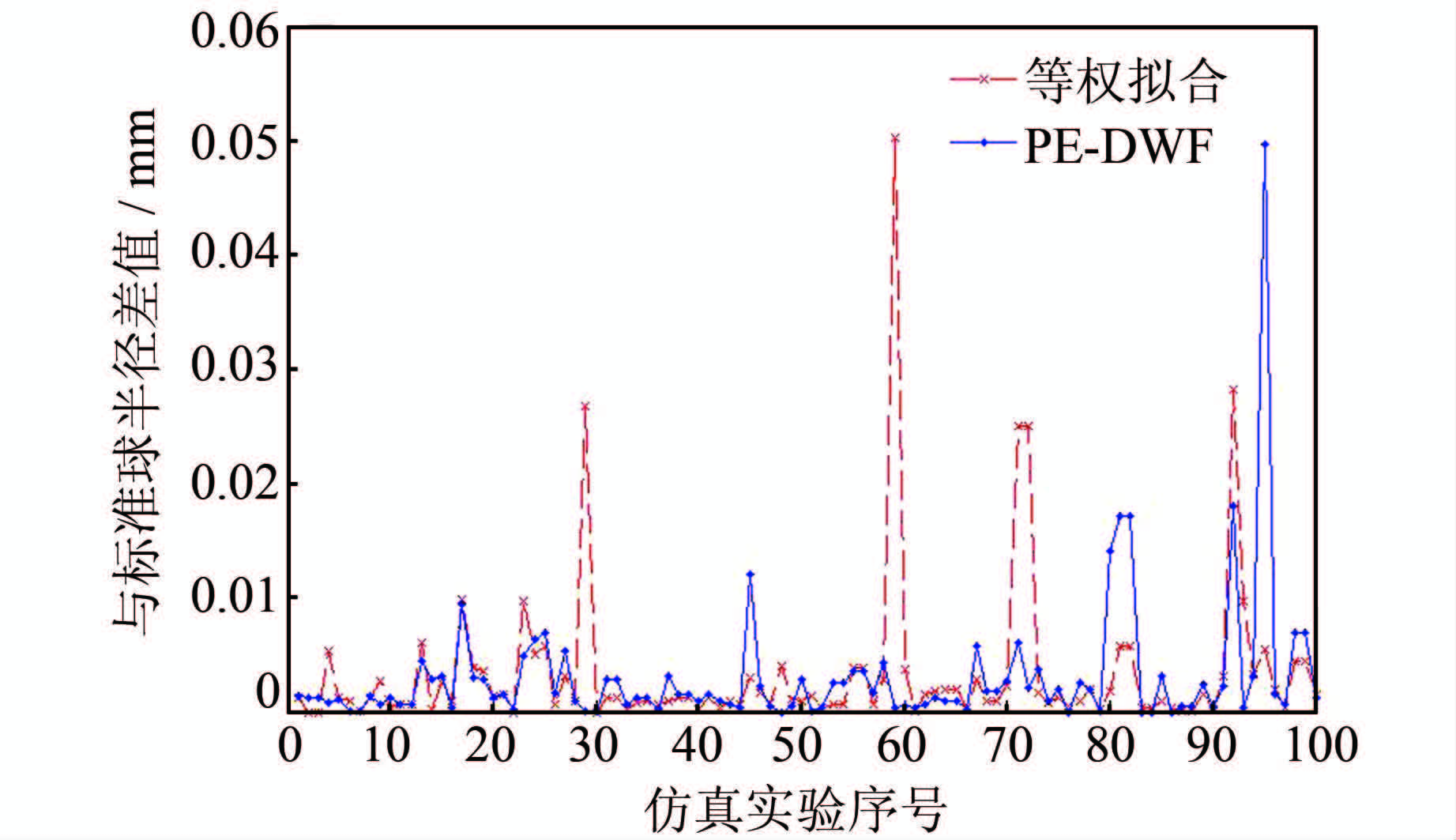
球等权拟合和PE-DWF拟合结果与标准球半径差值的比较如图 9所示。
|
| 图 9 与标准球半径差的比较 Fig. 9 Comparison of Standard Sphere on Radius Difference |
由图 9可知,球面的PE-DWF拟合与等权拟合相比,球半径误差平均减少10.22%。
综上可知,对于空间线、面、圆和球的拟合,PE-DWF拟合的精度较等权拟合有较明显的改进,在几何尺寸和空间姿态上都更接近真实值,并对部分等权拟合结果出现较大偏移现象的数据有较好的容错性。根据先验误差分解加权原理,在该仿真实验模拟的参数下,测站-测点连线与目标线或面的夹角越小,测点权值会越大,而当这些权值大的点测量误差的垂向分量又恰巧比较大时,分解加权拟合的效果就不那么好了,但在大多数情况下,PE-DWF还是对拟合精度有明显改进的。
4 结 语由于测量仪器测角精度和测距精度的差异,以及测量点相对测站位置关系的不同,导致各测点不同方向上的误差分量在数值和对拟合影响量上的不同,若都按等权进行拟合计算,必然难以达到最优的拟合精度。本文提出的基于先验误差分解加权拟合算法,根据测站-测点关系和几何体的空间姿态将测点误差分解为多个误差分量,并以其对拟合参数的影响量为各测点定权,使拟合出的几何体在尺寸和空间姿态上更接近实际参数。基于先验误差分解定权理论,针对非规则几何体或自由曲面的拟合算法将是下一步研究的内容。
| [1] | Goodman T, Tofallis C. Neutral Data Fitting by Lines and Planes [M]//Algorithms for Approximation.Berlin,Heidelberg :Springer, 2007 |
| [2] | Wang Jiexian, Ji Kaimin. Industrial Surveying Fitting [M]. Beijing: Surveying and Mapping Press, 2008: 15-60(王解先, 季凯敏. 工业测量数据拟合[M]. 北京: 测绘出版社, 2008:15-60) |
| [3] | Zhou Kai, Varadarajan K M, Zillich M,et al. Gaussian-weighted Jensen-Shannon Divergence as a Robust Fitness Function for Multi-model Fitting [J]. Machine Vision and Applications, 2013, 24(6):1 107-1 119 |
| [4] | Qiao Yu, Huang Xiyue, Chai Yi,et al. Corner Point Detection Based on Adaptive Line Approximation [J]. Journal of Chongqing University, 2003, 26(2):29-31(乔宇, 黄席樾, 柴毅,等. 基于自适应直线拟合的角点检测[J]. 重庆大学学报, 2003, 26(2):29-31) |
| [5] | Chen Tianli, Zhao Jianxun, Gao Yang, et al. Research of Satellite Antenna Dynamic Precision Calibration Method Based on the Three-dimensional Straight-line Fitting [J]. Electronic Measurement Technology, 2011, 34(3):99-101(陈天立, 赵建勋, 高扬,等. 基于三维空间直线拟合的卫星天线动态精密校准方法研究[J]. 电子测量技术, 2011, 34(3):99-101) |
| [6] | Guan Yunlan, Cheng Xiaojun, Shi Guigang. A Robust Method for Fitting a Plane to Point Clouds [J]. Journal of Tongji University (Natural Science), 2008, 36(7):981-984(官云兰, 程效军, 施贵刚. 一种稳健的点云数据平面拟合方法[J]. 同济大学学报(自然科学版), 2008, 36(7):981-984) |
| [7] | Zeng Qihong, Mao Jianhua, Li Xianhua,et al. Planar-Fitting Filtering Algorithm for LiDAR Points Cloud [J]. Geomatics and Information Science of Wuhan University, 2008, 33(1):25-28(曾齐红, 毛建华, 李先华,等. 激光雷达点云平面拟合过滤算法[J]. 武汉大学学报·信息科学版, 2008,33(1):25-28) |
| [8] | Pan Guorong,Chen Xiaolong.A New Method for 3D Circular Object Fitting [J]. Journal of Geodesy and Geodynamic, 2008,28(2): 92-94(潘国荣, 陈晓龙. 空间圆形物体数据拟合新方法[J]. 大地测量与地球动力学, 2008,28(2):92-94) |
| [9] | Ma Xiaping. Fitting Method for Space Plane Circle Parameters with Constraint Conditions [J]. Journal of Geodesy and Geodynamic, 2012, 32(6):86-89(马下平. 附有约束条件的空间平面圆参数的拟合方法[J]. 大地测量与地球动力学, 2012,32(6):86-89) |
| [10] | Ni Hui, Li Zhong, Song Hongxing. Moving Least Square Curve and Surface Fitting with Interpolation Conditions[C]. 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 2010 |
| [11] | Mansourifar H, Dehshibi M M, Bastanfard A. Shoulder Point Detection: A Fast Geometric Data Fitting Algorithm[C]. 2011 International Conference on Cyberworlds, CW, Alberta, Canada, 2011 |
| [12] | Capello E, Semeraro Q. Harmonic Fitting Approach for Plane Geometry Measurements [J].The International Journal of Advanced Manufacturing Technology, 2000, 16(4):250-258 |
| [13] | Wang Jinggeng. Analytic Geometry [M]. Beijing: Beijing Normal University Press, 2004(王敬庚. 空间解析几何[M]. 北京:北京师范大学出版社, 2004) |
 2015, Vol. 40
2015, Vol. 40


