文章信息
- 蒋振伟, 袁运斌, 欧吉坤, 王海涛
- JIANG Zhenwei, YUAN Yunbin, OU Jikun, WANG Haitao
- 基于站间单差相位绕转数据估计测站天线旋转速率的方法研究
- Precise Antenna Spin Rate Estimation Based on Between-Receiver Single-Difference Wind-up Observations
- 武汉大学学报·信息科学版, 2015, 40(10): 1334-1338
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1334-1338
- http://dx.doi.org/10.13203/j.whugis20130729
-
文章历史
- 收稿日期: 2013-12-03

GNSS载波相位是右旋极化电磁波信号[1],卫星天线与接收机天线之间的相对旋转会产生相位绕转误差。在卫星端,由于卫星姿态的调整产生的相位绕转误差可以采用模型进行精确修正[2];接收机端,主要采用星间差分等方式消弱相位绕转误差对定位的影响。相位绕转误差与高度角无关,在GNSS定位中被接收机钟差吸收。Kim等[3]详细分析了相位绕转误差对GNSS精密定位的影响。文献[4]则针对相位绕转误差对周跳探测的影响进行了分析。
虽然相位绕转在GNSS精密定位方面影响定位结果,但该误差也包含GNSS接收机天线旋转等有用信息,可以计算得到接收机天线旋转速率。天线旋转速率可应用于某些特定的场景,如发射中的火箭为了维持稳定的姿态,火箭自身将按一定速率旋转,装备GNSS接收机的火箭除了能够实时定位,还将获取火箭的旋转速率,进一步确定火箭的姿态是否符合设计的要求。实时确定火箭的旋转速率是非常重要的指标。García-Fernández等提出了一种利用单测站无几何距离Geometry-Free(GF)线性组合估计测站旋转速度的方法[5],该方法只能进行事后处理,并且需要引入外部高精度的电离层信息,同时估计GF线性组合中模糊度的处理策略,这就限制了测站旋转速率的估计精度。
本文提出了一种基于站间单差相位绕转数据估计测站天线旋转速率的方法,避免因引入外部的不准确信息而导致估计精度下降,并且可以实时估计测站天线的旋转速率。
1 天线旋转速率估计原理 1.1 GNSS双频基本观测方程在GNSS观测方程中,相位绕转主要影响载波相位观测数据。当GNSS接收机天线绕天顶方向旋转一周时,在载波相位观测值中,各个频率上将分别相应地改变一周。本文以GPS为例进行理论阐述,结论适用于其他卫星导航系统。GPS原始观测值的相位非差方程如下:
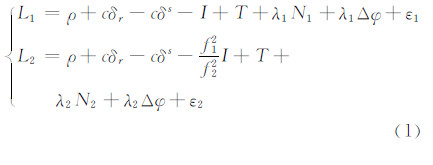
其中,L1和L2为载波相位观测值;ρ为站星间的几何距离;δr为接收机钟差;δs为卫星钟差;I为L1频率中的电离层误差;T为对流层误差;N1和N2为模糊度;Δφ为相位绕转误差;ε1和ε2为观测误差。
1.2 计算流动站与基准站之间无几何距离GF站间单差观测值无几何距离GF线性组合观测方程为:
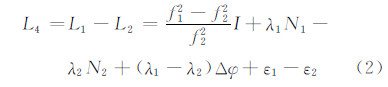
基准站无几何距离GF线性组合观测方程为:
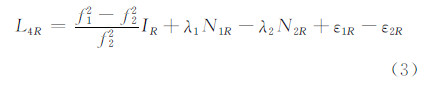
流动站无几何距离GF线性组合观测方程为:
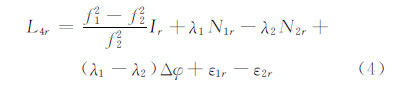
流动站与基准站之间无几何距离GF站间单差观测方程为:
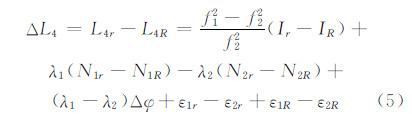
假设在整个实验过程中,基准站天线保持静止状态。基准站与流动站相距小于30 km,GNSS卫星高度远大于测站间距,通过观测值的测站间单差,卫星端的相位绕转误差可以忽略。通常情况下,太阳活动比较平稳,电离层活动亦相对平稳[6]。同时,假设基准站与流动站之间的距离较近(如不超过30 km),两观测站电离层之间有较强的空间相关性,站间单差可以大大削弱甚至消除电离层对旋转速率估计的影响,因而采用无几何距离GF站间单差的处理方式使实时估计流动站的旋转速率成为可能。若用户接收机天线旋转时,相位数据没有发生周跳或者发生周跳均已修复,则 λ1(N1r-N1R)与λ2(N2r-N2R)为模糊度,在观测过程中均为常数,ε1r、ε2r、ε1R、ε2R均为观测误差,(λ1-λ2)Δφ即为流动站接收机天线相位旋转对载波相位观测值的影响。
1.3 确定流动站天线旋转开始与结束时间统计流动站每颗卫星一定历元数目的GF线性组合观测值,作为判断天线旋转开始(结束)的依据。若某一历元所有卫星的GF线性组合观测值与统计结果相比,其差值超过设定的阈值,则认为该历元可能为天线旋转开始或者结束时刻。继续判断下一个历元所有卫星的GF线性组合观测值与统计结果的差值,如仍超过设定的阈值,则断定上一个历元为天线旋转开始或者结束时刻,同时记录相应时刻所有卫星的ΔL4。
1.4 测站天线旋转速率估计公式推导在§1.3中已经得到流动站天线旋转开始时间tstart和结束时间tend以及一颗卫星相应的Δ L4start与ΔL4end,则可以利用一颗卫星计算出测站天线在本段时间间隔中的平均旋转速率:

低高度角时,观测数据的信噪比较低,质量不佳,在计算过程中剔除高度角小于30°卫星的观测数据。每颗卫星计算结束后,将所有卫星的计算结果按照高度角加权平均,得到测站天线最终的旋转速率,进一步提高测站天线旋转速率估计的精度与稳定性。具体计算公式为:
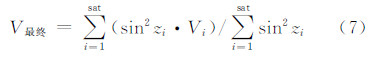
其中,sat表示卫星数; zi表示第i颗卫星高度角;Vi表示第i颗卫星计算的测站天线旋转速率。
如果实时计算流动站天线旋转速率,只需将式(6)中的tstart、tend、ΔL4start、ΔL4end替换为实时的数据即可。
2 天线旋转速率概略精度评定接收机载波测量噪声为1 mm,但实际观测值将受到多路径等各种误差的综合影响,因此本文假设L1与L2载波相位测量精度相同,均为2 mm。 由误差传播定律[7]以及式(2)、式(5)可知,无几何距离GF的精度为L1载波相位的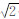 倍,站间单差无几何距离GF载波相位观测值ΔL4的测量精度为L1载波相位的2倍,即4 mm。L1与L2载波的波长之差为53.916 5 mm,即λ1-λ2=-53.916 5 mm。从式(5)可知,流动站天线旋转周 数Δφ为:
倍,站间单差无几何距离GF载波相位观测值ΔL4的测量精度为L1载波相位的2倍,即4 mm。L1与L2载波的波长之差为53.916 5 mm,即λ1-λ2=-53.916 5 mm。从式(5)可知,流动站天线旋转周 数Δφ为:
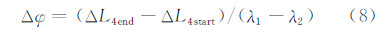
由式(8)可知,(Δ L4end-ΔL4start)的精度约为4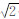 mm,则旋转周数Δφ的精度约为4
mm,则旋转周数Δφ的精度约为4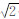 /53.916 5周。假设观测值采样率为1 Hz,旋转开始与结束时间为已知,间隔为T (s),由式(6)可得由一颗卫星流动站天线旋转平均速率估计的精度约为:
/53.916 5周。假设观测值采样率为1 Hz,旋转开始与结束时间为已知,间隔为T (s),由式(6)可得由一颗卫星流动站天线旋转平均速率估计的精度约为:
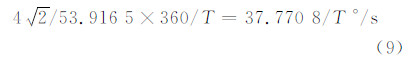
估计测站天线的最终旋转速率精度时,假设测站同时观测到N颗GNSS卫星,每颗卫星的计算结果按等权处理,根据误差传播定律,流动站天线最终旋转速率的精度为37.770 8/T/ N/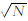 °/s。当N=8,T=60 s时,流动站天线最终旋转速率的精度为0.222 6 °/s。
°/s。当N=8,T=60 s时,流动站天线最终旋转速率的精度为0.222 6 °/s。
在基准站与流动站接收实测 GNSS数据,针对观测数据中可能存在周跳的情况,根据文献[4]中提出的方法,首先利用非差GF组合探测周跳,若所有卫星均发生周跳,则采用星间单差GF组合进一步探测,如发生周跳,则标记该历元数据为不可用,天线旋转速率计算将从后续未发生周跳的历元重新开始。在数据预处理结束后,基准站与流动站分别形成无几何距离GF组合观测值,将形成的GF组合观测值做站间差分。根据流动站的GF组合观测值,探测流动站天线旋转的开始时间tstart、结束时间tend以及相应的站间差分GF组合观测值ΔL4start与ΔL4end。根据式(6)即可得到单颗卫星计算的测站天线旋转速率,最后根据高度加权得到测站天线最终的旋转速率。测站天线的旋转速率估计的详细流程如图 1所示。

|
| 图 1 旋转速率估计的流程图 Fig. 1 Flow Chart of Spin Rate Estimation |
本文算例所用的数据采集于2014年2月15日,在中国科学院测量与地球物理研究所办公大楼楼顶架设两台Trimble NetR9接收机,其中一台接收机作为基准站,另外一台接收机作为流动站,旋转流动站天线,估计其天线旋转速率,观测时段为北京时间12:30:00至15:30:00,数据采样率为1 Hz。实验器材与实验场地如图 2所示,三脚架的为基准站,绿色回转平台的为流动站。

|
| 图 2 实验场地图 Fig. 2 Experimental Site |
实验步骤如下:① 两台接收机同时静止观测约30 min;② 逆时针旋转流动站的天线;③ 两台接收机静止观测约30 min;④ 先逆时针旋转流动站的天线,再顺时针旋转流动站的天线;⑤最后两台接收机再静止观测约30 min。
在实验步骤②、④中,采用秒表记录回转平台旋转每圈所用的时间(表 1),求出回转平台的平均旋转速率(表 2),并与GNSS计算的结果进行对比。
| 回转平台每圈旋转用时 |
步骤②中逆时针 | 59.92,60.92,71.29,62.24,67.27,68.50,72.84,68.52,69.65,66.43,70.84,67.62,68.95,69.85,64.76,72.90,69.71,72.84,67.63,67.31 |
| 步骤④中逆时针 | 63.11,63.51,62.16,60.75,63.47,60.00,57.29,60.07,60.82,59.00 |
| 步骤④中顺时针 | 62.13,61.26,58.88,59.63,60.36,61.23,60.80,59.59,59.49,58.97 |
| 根据GNSS计算 | 根据秒表计时计算 | 标准差 | |
| 步骤①中静止段 | 0.005 1 | 0 | 0.296 0 |
| 步骤②中逆时针 | 5.253 3 | 5.294 5 | 0.408 0 |
| 步骤③中静止段 | 0.017 1 | 0 | 0.238 6 |
| 步骤④中逆时针 | 5.946 2 | 5.899 8 | 0.437 3 |
| 步骤④中顺时针 | 5.968 2 | 5.976 7 | 0.351 0 |
| 步骤⑤中静止段 | 0.018 1 | 0 | 0.269 9 |
为详细分析实验结果,本文选取在整个实验过程均可见的两颗共视卫星(18号、22号)的数据进行分析。其余卫星的结果与之类似。
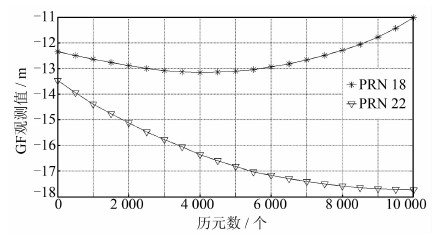
4.2 实验结果及分析由图 3可以看出,基准站GF组合观测值变化平稳,同时说明在本实验中电离层变化相对稳定的假设是正确的。
|
| 图 3 基准站18、22号卫星GF观测值 Fig. 3 Base Station GF Observations of PRN 18 and PRN 22 |
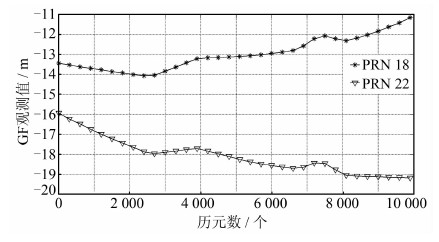
由图 4可知,由于接收机天线的旋转导致流动站GF组合载波相位观测值发生渐变,如在步骤④的旋转中,流动站天线顺时针与逆时针旋转的周数大致相同,GF组合载波相位观测值首先变大然后又快速变小,直至恢复到没有旋转流动站天线的状态。如果接收机天线停止旋转,则GF组合观测值恢复平稳,且其变化趋势与基准站的变化趋势完全吻合。从式(4)中可知,该平稳变化的趋势主要来自于电离层的平稳变化。从图 4中可以明显地看出旋转流动站天线对相位观测值渐变的影响,该影响反映了接收机天线的旋转速率。
|
| 图 4 流动站18、22号卫星GF观测值 Fig. 4 Rover Station GF Observations of PRN 18 and PRN 22 |
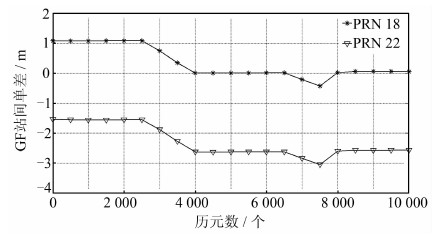
从图 4和图 5可知,旋转开始和结束时间非常明显,天线旋转开始与结束的具体时间确定采用§1.3所述的方法。利用精确的GF站间单差载波相位变化量则可以直接得到接收机天线的旋转速率。
|
| 图 5 18、22号卫星GF站间单差观测值 Fig. 5 Between-Receiver Single-Differences of GF Observations for PRN 18 and PRN 22 |
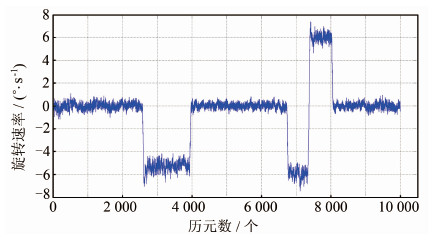
图 6中的天线旋转速率为在短时间内(如30 s)的平均天线旋转速率。由表 2可知,根据本文方法计算的天线旋转速率与秒表计时方式计算的天线旋转速率(表 2)之差小于0.5 °/s,标准差小于0.5 °/s。在天线旋转速率图 6中,流动站天线旋转停止之后,流动站天线旋转速率立刻降为零,与实际情况完全吻合,这也进一步说明载波相位观测值可以精确反映接收机天线的旋转状态。天线旋转速率的方向(顺、逆时针)可以通过计算得到的正负号确定。在本实验中,正号代表顺时针方向,负号代表逆时针方向。
|
| 图 6 接收机天线旋转速率估计 Fig. 6 Rotating Rate Estimation of Receiver Antenna |
本文提出了一种精确估计GNSS用户天线旋转速率的方法。经实验验证,该方法合理可行,并且具有估计实时天线旋转速率的能力,为接收机姿态的实时确定提供了基础,也对GNSS接收机特定场合的应用提供了有效方法。
流动站天线旋转速率的实时估计受限于基准站数据的实时传输,如果基准站数据传输中断,将导致流动站天线的旋转速率无法估计,但仍可以采用后处理的方式得到高精度的流动站天线旋转速率。本文实验仅在水平面内旋转,至于其余自由度的旋转暂时未考虑。在本文讨论中,仅考虑流动站天线存在相位绕转的现象,而基准站天线处于静止状态。本文实验是在较为理想的条件下进行的,即流动站基本处于静止状态,流动站与基准站距离较近,对流层等误差相关性强,站间差分能够较好地消弱公共误差,如将本文方法应用于流动站与基准站距离较远等复杂的实际场合,则流动站天线旋转速率的估计精度将会下降。估计流动站接收机的旋转速率应该尽量采用高采样率的观测数据(如50 Hz),以保证旋转速率估计的分辨率和灵敏度。
本文虽然基于GPS讨论了测站天线旋转速率的估计方法,但该方法可以应用于北斗等其他卫星导航系统测站天线旋转速率的估计。
| [1] | Navstar GPS Space Segment/Navigation User Interfaces (ICD-GPS-200D), Revision D[S]. USA:GPS Joint Program Office, 2004 |
| [2] | Wu J T, Wu S C, Hajj G A, et al. Effects of Antenna Orientation on GPS Carrier Phase[J]. Manuscripta Geodaetica, 1992, 18(2):91-98 |
| [3] | Kim D, Serrano L, Langley R B. Phase Wind-up Analysis: Assessing Real-time Kinematic Performance[J]. GPS World, 2006, 17(9): 58-64 |
| [4] | Yi Wenting, Song Weiwei, Shi Chuang, et al. Influences of Wind-up on Data Preprocessing in Real-time Dynamic PPP[J]. Geomatics and Information Science of Wuhan University, 2012, 37(11): 1 341-1 344(易文婷,宋伟伟,施闯,等. 相位绕转误差对实时动态PPP数据预处理的影响分析[J]. 武汉大学学报·信息科学版,2012, 37(11): 1 341-1 344) |
| [5] | García-Fernández M, Markgraf M, Montenbruck O. Spin Rate Estimation of Sounding Rockets Using GPS Wind-up[J]. GPS Solutions, 2008, 12(3): 155-161 |
| [6] | Yuan Yunbin. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS[D]. Beijing: Chinese Academy of Sciences, 2002(袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 北京: 中国科学院研究生院, 2002) |
| [7] | Surveying Adjustment Group in School of Geodesy and Geomatics, Wuhan University. Error Theory and Fundation of Surveying Adjustment[M]. Wuhan:Wuhan University Press, 2003 (武汉大学测绘学院测量平差学科组[M]. 误差理论与测量平差基础[M]. 武汉:武汉大学出版社, 2003) |
 2015, Vol. 40
2015, Vol. 40


