文章信息
- 高晓, 戴吾蛟, 张超, 余文坤
- GAO Xiao, DAI Wujiao, ZHANG Chao, YU Wenkun
- 多星座组合精密动态定位的抗差扩展Kalman滤波方法研究
- Robust Extend Kalman Filtering Method Based on Precise Relative Positioning by Using Multi-constellation Integrated System
- 武汉大学学报·信息科学版, 2015, 40(10): 1329-1333
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1329-1333
- http://dx.doi.org/10.13203/j.whugis20130668
-
文章历史
- 收稿日期: 2014-03-06

GNSS多星座组合定位可以增加可视卫星,改善卫星的空间分布结构,削弱单系统有色噪声的影响,提高用户PNT(positioning,navigation and timing)服务的精度与可靠性,因此,多星座组合定位成为GNSS技术发展的重要趋势[1, 2]。由于多星座组合系统的观测数据源于各自独立的卫星系统,因此,数据融合解算方法成为多星座组合定位的关键技术。高效的数据融合定位算法可以充分发挥组合系统的优势,提高定位精度和系统的整体性能。Kalman滤波(Kalman filter,KF)是一种高效率的动态滤波算法,在组合定位领域具备强大的生命力[3]。
标准KF算法适用于线性滤波领域,鉴于GNSS观测方程非线性方程的特点,扩展Kalman滤波算法(extend Kalman filter,EKF)被广泛应用于GNSS定位领域。然而,EKF算法同样需要满足的必备假设条件之一是观测数据服从正态分布。当观测值存在异常扰动,影响观测值的正态分布特征时,标准EKF算法无法得到最优估计,甚至严重偏离真实值,影响PNT服务的精度与可靠性[4]。文献[5, 6]引入抗差估计的思想抑制观测异常的影响,抗差EKF算法应用于GNSS领域,并取得了较好的效果[5, 6]。但是上述研究仅采用模拟观测数据,未考虑实测观测数据的复杂性及不同系统观测数据的系统性差异。为此,本文首先在一个相对开阔的环境采集GPS/GLONASS/BDS观测数据,然后采用虚拟掩模(对待处理事物进行覆盖的特定图像或物体)遮挡卫星,模拟得到各种不同的遮挡观测环境的实测数据,并利用该数据进行基于抗差M估计理论的抗差EKF算法研究。
1 多星座组合相对定位函数模型GPS、GLONASS与BDS均采用距离交会定位,设测站i在某历元观测到卫星 p,忽略初始相位偏差与硬件延迟,载波相位观测方程可表示为[7]:

式中,上标为卫星;下标为测站;L为测站载波相位观测值(m);ρ为相应的卫地距(m);c为真空光速(m/s);dts为卫星钟差,dtr为接收机钟差;λ为载波波长(m);N为整周模糊度参数;T、I分别为对流层与电离层时延(m);ε为相位观测噪声。
多星座组合定位时,选择参考卫星进行双差建模的理想方式是仅选择一颗参考卫星,其余观测卫星均与该卫星进行差分。但由于不同系统的载波波长存在明显差异,特别是GLONASS卫星,因此,目前常用的方式是为各GNSS系统选择各自的参考卫星,组建差分方程后再统一解算。
设测站i、j同时观测卫星p、q,则构建如下的双差观测方程(q为参考卫星):

式中,对流层与电离层延迟经双差模型基本消除,其他空间相关性误差也得到了较好的削弱,同时,接收机钟差与卫星钟差参数均已消去。因此,短基线相对定位中,双差观测方程未知参数的个数大大减小,大幅度降低了数据处理的工作量[8]。
在多星座组合相对定位时,由于GPS和BDS均采用CDMA编码方式,其观测值构建的非差、单差以及双差模型结构保持一致,GLONASS系统采用FDMA技术,不同卫星的波长有所差异,因此,对于GLONASS,双差观测方程参考卫星的单差模糊度参数无法消除。该参数通过伪距观测值取初始值,待双差模糊度确定后再搜索其精确值。
2 组合定位抗 差EKF算法 2.1 标准扩展Kalman滤波标准扩展Kalman滤波(EKF)的基本原理是先围绕估计点进行一阶泰勒展开,然后利用Kalman滤波公式进行最优估计。标准EKF的递推公式为[9]:
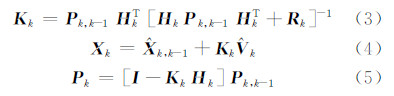
其中,P k是状态噪声协方差矩阵; R k为观测噪声协方差矩阵。在多系统组合定位时状态噪声保持一致的前提下,观测噪声存在明显的系统性差异,因此,有必要确定不同系统观测值的方差。由于验后估计严重影响动态定位的实时性,因此,需要确定不同系统的先验方差比。依据笔者以前的研究结果[10, 11],GPS、GLONASS与BDS观测值的先验方差比可确定为1∶4∶1。
分析EKF公式可知,滤波最优估值 X k由观测新息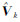 与状态估值
与状态估值 共同决定,滤波增益 K k则决定了两者的权重。滤波增益值越大,观测新息权重越大,状态估值权重变小。
共同决定,滤波增益 K k则决定了两者的权重。滤波增益值越大,观测新息权重越大,状态估值权重变小。
EKF算法同样要求观测信息的先验误差满足一系列假设条件,当观测信息存在扰动异常时,EKF滤波算法失真甚至不收敛[8]。GNSS实际测量中,观测环境复杂多变,观测异常时有发生,标准EKF算法难以得到有效应用。因此,有必要引入抗差估计的思想抑制观测异常的影响,保证滤波的可靠性。那么,合理确定滤波增益成为抑制观测异常影响的关键。
分析式(3)可知,在状态噪声保持一定的前提下,观测噪声协方差矩阵对滤波增益有显著影响。基于抗差估计理论的方差膨胀模型通过放大观测异常值的方差控制观测异常的影响,其抗差性能的有效性取决于等效协方差矩阵的合理性。IGGIII模型作为一种经典的抗差模型[12],其基本原理是直接将标准化残差划分三段,结合原有的观测方差构建抗差等价方差阵。抗差因子确定之后,即可确定观测新息的等价协方差矩阵:
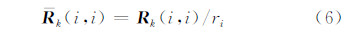
ri采用IGGIII模型,其公式如下[13]:

式中,vi为标准化残差,其计算公式为[14]:
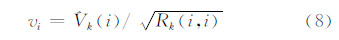
其中,Vk(i)为tk历元新息向量 V k的第i个分量;Rk(i,i)为 V k的协方差矩阵 R k对角线上的第i个元素。
抗差EKF算法需进行迭代计算,以确定最优抗差解。为避免迭代陷入无限死循环,同时保证动态定位的实时性,需设定迭代终止条件限定迭代次数:
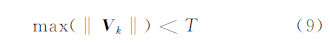
式中,T为设定的阈值,可依据采样频率进行设定。同时,依据采样频率有必要设定最大迭代次数,保证解的实时性。
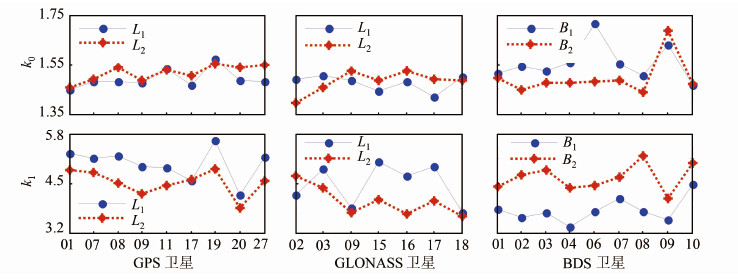
2.3 抗差分位参数的确定IGGIII模型中,k0与k1是分位参数,可依据经验进行确定。但是,不同的参考文献给定的分位参数有明显差异,本文利用实测超短基线数据计算不同系统观测卫星站间的单差残差,在假设残差满足高斯分布的前提下,分别以1倍中误差与3倍中误差为界计算对应的分位参数 k0与k1,结果如图 1所示。由图 1可知,利用三种独立的观测数据解算得到的分位参数并无明显的系统性差异,k0的取值范围为1.35~1.75,k1的取值范围为3.2~5.8。较之给定的经验值[15](k0:1.5~3.0;k1:2.5~8.0),该取值范围明显变小,有利于建立更有效的抗差模型。
|
| 图 1 基于不同卫星系统单差残差序列确定IGGIII模型的分位参数 Fig. 1 Fractile Factors of IGGIII Model Based on Different GNSS Single Difference Residuals |
本次实验数据采用上海司南K508板卡测量混合三星八频数据,频点包括GPS(L1/L2/L5)、GLONASS(L1/L2)和BDS(B1/B2/B3),观测数据采样间隔为10 s,卫星截止高度角设定为15°。基线解算时,仅考虑观测数据前两个频点数据。为模拟实际应用中复杂的测量环境(如变形监测),设计了三个不同的遮挡模板(掩模),如图 2所示,被遮挡卫星的观测值将剔除,从而得到4套观测数据,然后分别采用标准EKF算法与抗差EKF算法进行解算。

|
| 图 2 模拟遮挡复杂观测环境的掩模 Fig. 2 Three Masks to Simulate Complex Environments |
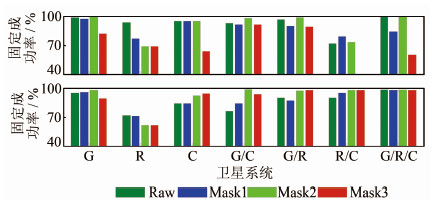
图 3中的上下两个子图为动态相对定位下标准EKF和抗差EKF两种算法所得到的固定解比重(即模糊度固定率)。图中,大写字母G、R、C分别代表GPS、GLONASS和BDS(下文含义一致)。
|
| 图 3 标准EKF算法与抗差EKF算法的固定成功率比较 Fig. 3 Comparison of Fixed-rate Between Classical EKF Method and Robust EKF Method |
从图 3可以看出,随着掩模的变化,固定解比重有所变化。大多数情况下,由于掩模遮挡,可观测卫星数减少,模糊度固定率都有所降低,其中模板3的掩盖区域最大,可视卫星数急剧减少,固定率最低。但掩模2环境下的固定率反而优于原始数据,这主要是由于被遮挡的卫星在测段内的卫星高度角较低,相当于剔除了质量较差的观测数据,反而提高了固定成功率。对比图 3中的上下两个子图可以看出,当进行组合定位时,采用抗差EKF算法的固定成功率更高,而在部分模拟环境中的单系统定位的固定成功率反而更低,其原因是单系统中的多余观测较少,而导致抗差的可靠性较低。
图 4中的上下两个子图分别为采用标准EKF和抗差EKF得到的动态相对定位结果的坐标残差序列的RMS值。从图 4可以看出:①单系统定位时,GPS精度最高,BDS次之,GLONASS的定位精度最差;②当观测环境存在遮挡时,GPS所受的影响最小,其原因是GPS可观测卫星数多,而BDS由于其独特的静止轨道和同步轨道星座的设计,不同的遮挡环境,其定位结果差异较大;③采用标准EKF算法时,组合系统的定位结果较之单系统无明显改善,这是由于观测值中存在粗差所致;④组合系统定位时,采用抗差EKF算法的定位精度有明显提高,其中G/R/C系统组合定位的精度最高;而单系统定位时,采用抗差EKF的精度反而有所降低,这是由于单系统中多余观测较少,而使抗差的可靠性较低所致。

|
| 图 4 标准EKF算法与抗差EKF算法解算得到的坐标残差序列的RMS值 Fig. 4 RMS Values Using Classical EKF Method and Robust EKF Method with Different Masks |
由于标准EKF算法难以抵抗观测异常的影响,本文利用基于IGGIII抗差方案的抗差EKF算法进行多星座组合定位解算,并对实测数据的站际单差残值进行统计分析,得到了抗差分位参数的经验值。采用开阔环境得到的实测多星座观测数据,通过掩模遮挡模拟复杂的GNSS观测环境,对抗差EKF算法的定位效果进行了实验分析。结果表明,在多星座组合定位中,冗余信息较多,抗差EKF算法可有效提高模糊度的固定成功率与定位精度;在单系统定位中,由于多余观测较少,抗差系统的可靠性较低,从而导致定位精度降低。
| [1] | Yang Yuanxi,Li Jinlong,Xu Junyi,et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Sci Bull,2011,56(26):2 813-2 819 |
| [2] | Yang Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica,2010,39(1):1-6 (杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报,2010,39(1):1-6) |
| [3] | Song Yingchun. Research on Kalman Filter in Kinematic Positioning[D].Changsha:Central South University, 2006 (宋迎春. 动态定位中的卡尔曼滤波研究[D].长沙:中南大学, 2006) |
| [4] | Cui Xianqiang. Study on Extension and Application of Adaptive Robust Filtering Theory for Controlling Influence of Colored Noise in Kinematic Positioning[D]. Xi'an:Chang'an University, 2012(崔先强. 动态定位有色噪声自适应抗差滤波理论的拓展与应用研究[D]. 西安:长安大学,2012) |
| [5] | Wang Jian, Wang Jinling, Gao Jingxiang. Study on GNSS Navigation Model Based on EKF[J]. Journal of China University of Mining & Technology, 2008, 37 (4): 473-477 (王坚,王金岭,高井祥. 基于抗差EKF的GNSS导航模型研究[J]. 中国矿业大学学报,2008,37(4):473-477) |
| [6] | Xu Changhui, Gao Jingxiang, Wang Jian. Robust Kalman Filtering of GNSS/INS Integrated System[J]. Journal of China University of Mining & Technology, 2010, 39(5): 773-778 (许长辉,高井祥,王坚. GNSS/INS组合系统的抗差卡尔曼滤波[J]. 中国矿业大学学报,2010,39(5):773-778) |
| [7] | Yu Wenkun. GPS/GLONASS Combined Positioning Technology and Its Application in Deformation Monitoring[D].Changsha:Central South University, 2013 (余文坤. GPS/GLONASS组合定位技术及其在变形监测中的应用[D]. 长沙:中南大学,2013) |
| [8] | Xu Guochang. GPS Theory, Algorithms and Applications[M]. 2nd ed.Berlin,Heidelberg:Springer-Verlag,2007 |
| [9] | Zhao Changsheng, Tao Benzao. Robust Kalman Filtering of Linear System with Colored Noises[J]. Geomatics and Information Science of Wuhan University, 2007, 32(10): 880-882 (赵长胜,陶本藻.有色噪声作用下的抗差卡尔曼滤波[J]. 武汉大学学报﹒信息科学版,2007,32(10):880-882) |
| [10] | Gao Xiao, Dai Wujiao. Robust Stochastic Model of Combined GPS and GLONASS [J]. GNSS World of China, 2012, 37(6): 17-20,25 (高晓,戴吾蛟. GPS/GLONASS组合定位的抗差Helmert方差估计模型[J]. 全球定位系统,2012,37(6):17-20,25) |
| [11] | Gao Xiao, Dai Wujiao. Determination of Prior Weight Ratio for Combined GPS-BD2 Positioning Based on Variance Component Estimation[J]. Journal of Geodesy and Geodynamics, 2013, 32(2): 136-138 (高晓,戴吾蛟.基于方差分量估计确定GPS/BD2组合定位先验权比[J].大地测量与地球动力学,2013,32(2):136-138) |
| [12] | Yang Y. Robust Estimation for Dependent Observations[J]. Manuscripta Geodeatica,1994,19(1):10-17 |
| [13] | Yang Yuanxi, Song Lijie, Xu Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31 (2): 95-99 (杨元喜,宋力杰,徐天河.大地测量相关观测抗差估计理论[J]. 测绘学报,2002,31 (2): 95-99) |
| [14] | Wu Xixiu. Research on Kalman Filtering for Dynamic Deformation Monitoring[D]. Changsha:Central South University, 2011 (伍锡绣. 动态变形监测中的Kalman滤波方法研究[D]. 长沙:中南大学,2011) |
| [15] | Wen Yuanlan, Yang Yuanxi, Wang Wei. Research on Satellite Presicion Orbit Robust Estimation[J]. Chinese Journal of Space Science, 2001, 21(4): 341-350 (文援兰,杨元喜,王威. 卫星精密轨道抗差估计的研究[J]. 空间科学学报,2001,21(4):341-350) |
 2015, Vol. 40
2015, Vol. 40


