文章信息
- 姚宜斌, 刘强, 江国焰, 张良
- YAO Yibin, LIU Qiang, JIANG Guoyan, ZHANG Liang
- 华北地区应变率及其精度评定
- Strain Rate and Its Accuracy Assessment in North China
- 武汉大学学报·信息科学版, 2015, 40(10): 1317-1323
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1317-1323
- http://dx.doi.org/10.13203/j.whugis20140001
-
文章历史
- 收稿日期: 2014-01-01

2. 河北师范大学资源与环境科学学院, 河北 石家庄, 050024;
3. 中国地震局地质研究所, 北京, 100029
2. College of Resources and Environment Science, Hebei Normal University, Shijiazhuang 050024, China;
3. Institute of Geology, China Earthquake Administration, Beijing 100029, China
GPS既可以获得地壳长趋势的构造变化信息,也可以捕捉地壳短暂的微动态变化。目前,高精度GPS已经成为研究地壳水平运动的重要技术手段。自我国“九五”期间国家投资建设的重大科学工程——中国地壳运动观测网络项目(crustal movement observation network of China,CMONOC)建立以来,华北地区一直是GPS重点观测区域[1]。目前,华北是我国GPS点位密度最高、资料积累时间最长、复测周期最多的地区,很多学者对该区的水平运动与应变特征及断裂带活动习性进行了大量研究[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]。然而,华北地区是一个形变信息较弱、干扰较强的地区,对于计算出来的华北地区的应变率的精度却少有评估,本文利用文献[13]中公布的CMONOC的GPS速度数据,基于连续变形假设,采用多面函数双调和法对该区域的建模和滤波数据进行了处理[14],在球面上整体计算出华北地区地壳东西向线应变率、南北向线应变率、北东向剪应变率,并初步评估了其精度。
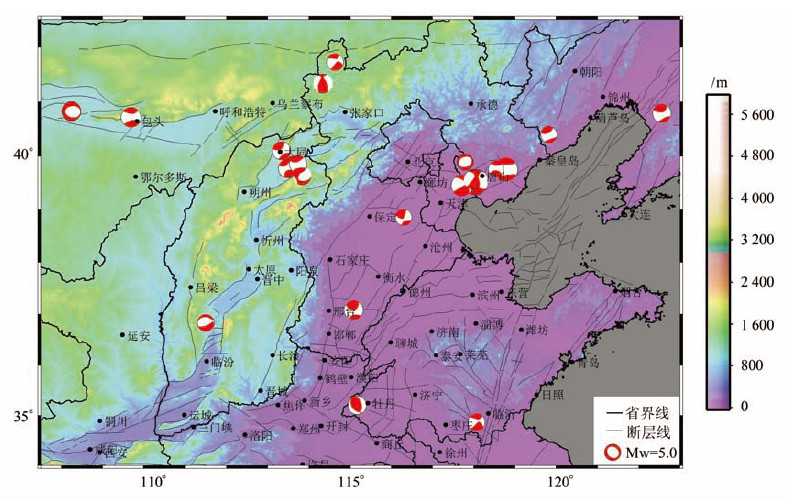
1 华北地区构造特征本文研究区域为经度为107.5°~123° E、纬度为34°~42.5° N的矩形区域,如图 1所示。图 1采用GTOPO30为底图(https://lta.cr.usgs.gov/GTOPO30),震源机制解是由哈佛大学(http://www.globalcmt.org/)下载的1976年7月28日唐山大地震之后到2013年11月8日Mw≥5.0的中强震震源机制解[15],其中断层线参照邓起东等的研究成果[16, 17]。
|
| 图 1 华北地区活动构造背景图 Fig. 1 Active Tectonic Background in North China |
华北地区中生代经历了大规模的裂陷伸展、岩石圈减薄及岩浆活动,地质构造复杂[8]。华北地壳平面分布特征为:西部鄂尔多斯盆地基底结构完整,为稳定的古大陆地壳;中部隆起区太行山及北部阴山、燕山隆起区中部地壳和下地壳局部区域轻微速度逆转;东部裂陷盆地地壳结构复杂,基底下陷、破碎,壳内介质松散、速度低,莫霍面上隆、地壳减薄,横向结构差异明显,显示了新生地壳构造特征[6, 11]。由图 1可以看出,1976年唐山地震以来,华北地区中强震大部分发生在正断层和走滑断层上,唐山、大同附近发生的中强震较多。
2 应变率计算及其精度评定 2.1 应变率计算方法Hardy教授于1968年提出了多面函数双调和方法,然而由于最初并不了解多面函数双调和法就是一种调和法,在1971年的文献中称该方法为多面函数拟合法,因此国内外多称Hardy的方法为多面函数拟合法[18, 19]。武艳强等将其用于球面上整体求解GPS应变率场[14, 20];杨博等(2010)提出多面函数双调和法具有滤波的功能,求解GPS应变率场的数学模型为:
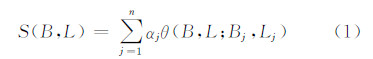
式中,B 、L 为纬度和经度;n为结点数;α为待定系数;θ(B,L;Bj,Lj)为核函数,其一般形式为:

式中,d为球面距离;δ为光滑因子;β的取值决定了核函数的类型,β=1/2为正双曲面模型,β=-1/2为倒双曲面模型,β=3/2为三次曲面模型。
对目标格网点的经纬向速度求偏导,可以计算出格网点的应变率[20, 21, 22]:

式中,εe、εn、εne分别为地壳东西向线应变率、南北向线应变率、北东向剪应变率[23];Vn 、Ve为纬向、经向速度;R 为地球平均曲率半径。
2.2 精度评定对于式(1)、式(2),当建模点数等于结点数时,可直接利用误差传播定律来评价结果的精度;当建模点数大于结点数时,一般采用最小二乘法进行求解,因此可以利用残差平方和与误差传播率来评价结果的精度。其中α的单位权方差为:
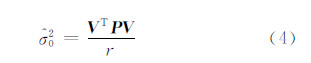
式中,V为残差; P 为权;r为自由度。
建模时,由式(1)、式(2)可得目标点经纬向的速度和α的方差。利用α的方差阵和误差传播率,通过式(1)可以得到速度的方差阵为:

式中,Dαn和Dαe分别为多面函数双调和法建模系数α在经纬向上的方差阵;本文取β=1/2;θ 为:
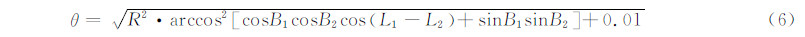
利用α的方差阵和误差传播率,通过式(1)可以得到各偏导数的方差阵为:

式中,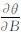 和
和 分别为θ在纬度和经度上求偏导,对于本文为:
分别为θ在纬度和经度上求偏导,对于本文为:
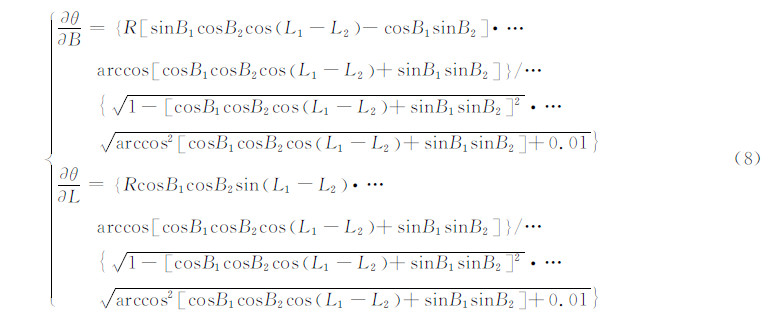
利用式(3)、式(5)、式(7),结合误差传播率,可以求得各应变率分量方差为:
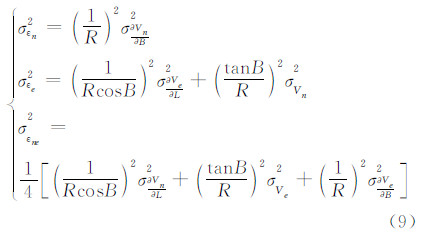
首先采用CMONOC的所有GPS数据,利用多面函数双调和法进行数值逼近0.5°×0.5°间隔点的速度场,然后从逼近的速度场中选择多面函数双调和法的结点以1°步长推估目标点的速度及应变率[24],并利用式(1)、式 (2)、式 (3)、式 (9)结合误差传播率评估计算东西向线应变率、南北向线应变率、北东向剪应变率的精度。本文在计算应变率时,距离单位为m,速度单位为m/s。
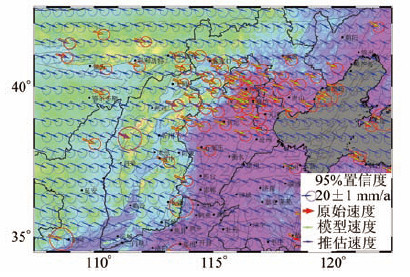
3.1 多面函数双调和法的模型建立效果采用的CMONOC分布于华北区域的数据如图 2中红色较粗箭头所示,多面函数双调和法数值逼近的0.5°×0.5°间隔点的速度结果如图 2中蓝色较细箭头所示,所建立的模型推估已知点的速度结果如图 2中绿色较细箭头所示。图 2中所有速度都画有误差椭圆,图例中除外。
|
| 图 2 原始观测速度和推估速度分布 Fig. 2 Distribution of the Original Velocity and Estimate Velocity |
由图 2可以看出,推估已知点的速度与原来的原始观测速度相差很小,并且对照图例由推估目标点的误差椭圆速度可知,数值逼近的0.5°×0.5°间隔点速度和推估的目标点的速度符合整体速度场的趋势,并且所建立的多面函数双调和模型发挥了多面函数双调和的滤波作用。本文统计了建模速度与实际速度之间的差值,其统计结果见表 1。
| 最小值 | 最大值 | 标准差 |
| E向 | -3.907 0 | 6.826 4 | 1.210 5 |
| N向 | -3.220 0 | 3.741 4 | 1.255 8 |
由图 2和表 1中速度差值的统计值可以得出,模型建立得良好,推估目标点的速度非常可信。
由于篇幅所限,本文仅给出了东西向线应变率、南北向线应变率、北东向剪应变率的精度。精度评价原则为:

式中,ε为应变率;σε 为应变率的中误差,也就是当应变率大于应变率的中误差时,该应变率的值可靠,反之则不可靠。
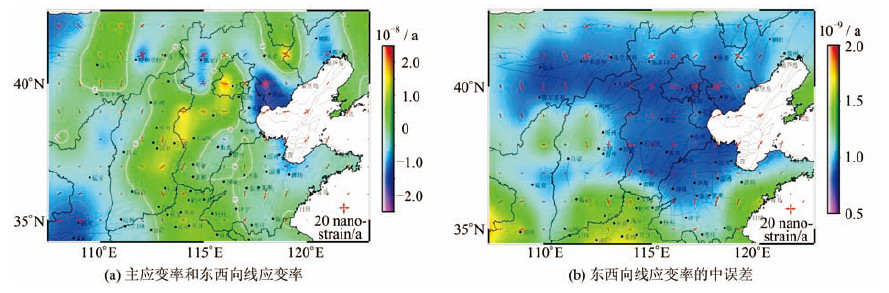
3.2 华北地区东西向线应变率及精度利用式(3)计算得到的华北地区的主应变率及东西向线应变率如图 3(a) 所示,东西向线应变率的中误差如图 3( b)所示。
|
| 图 3 华北地区主应变率和东西向线应变率及其中误差 Fig. 3 North China Principal Strain Rate, East-West Linear Strain Rate and Its Standard Deviation |
由图 3( a)和图 3( b)可以看出,利用多面函数双调和法计算得到的华北地区主应变率基本呈北东东压、北北西张的状态,东西向线应变率的区间为-2.5×10-8/a ~2.5×10-8/a,东西向线应变率的中误差的区间为±0.5×10-9/a~±2.0×10-9/a。东西向线应变率的中误差较小的区域与真实GPS速度场的区域相符。从东西向线应变率的中误差和东西向线应变率的大小比值角度看,东西向线应变率的结果具有很高的精度。
3.3 华北地区南北向线应变率及精度利用式(3)计算得到华北地区的主应变率及南北向线应变率如图 4 (a)所示,南北向线应变率的中误差如图 4( b)所示。

|
| 图 4 华北地区主应变率和南北向线应变率及其中误差 Fig. 4 North China Principal Strain Rate, South-North Linear Strain Rate and Its Standard Deviation |
由图 3(a) 和图 3( b)可以看出,利用多面函数双调和法计算得到的华北地区南北向线应变率的区间为-1.5×10-8/a ~2.5×10-8/a,南北向线应变率的中误差的区间为±0.5×10-9/a~±2.0×10-9/a。南北向线应变率的中误差较小的区域也与真实GPS速度场的区域相符。从南北向线应变率的中误差和南北向线应变率的大小比值角度看,南北向线应变率的结果也具有很高的精度。
3.4 华北地区北东向剪应变率及精度利用式(3)计算得到华北地区的主应变率及北东向剪应变率如图 5( a)所示,北东向剪应变率的中误差如图 5( b)所示。

|
| 图 5 华北地区主应变率和北东向剪应变率及其中误差 Fig. 5 North China Principal Strain Rate, North\|East Shear Strain Rate and Its Standard Deviation |
由图 5 (a)和图 5(b) 可以看出,利用多面函数双调和法计算得到的华北地区北东向剪应变率的区间为-1.8×10-8/a ~1.5×10-8/a,北东向剪应变率的中误差的区间为±0.5×10-9/a~±1.5×10-9/a。北东向剪应变率的中误差较小的区域也与真实GPS速度场的区域相符。从北东向剪应变率的中误差和北东向剪应变率的大小比值角度看,南北向线应变率的结果也具有很高的精度。
4 结 语由于计算应变率时需要通过求微分等过程,误差经历多次传播之后会被放大,做好速度场的滤波是避免出现应变率的中误差大于应变率的不可靠结果的良好手段。本文采用了多面函数双调和法进行了建模、滤波并最终计算出华北地区构造应变率的结果,该结果具有很高的精度,符合华北地壳的平面分布特征,与杨国华等计算的结果相符得很好[12]。另外,计算得到的应变率的中误差较小的区域与真实GPS速度场的区域相符,也印证了合理布置GPS实测点也是进一步提高应变率的结果精度的良好方法。
致谢:感谢中国地震局地震预测研究所江在森研究员和武艳强博士在计算应变率方法上的指导,中国地震局第一监测中心杨国华研究员在多面函数双调和滤波方法上的指导以及武汉大学测绘学院陈浩朋博士和李孟奎博士在震源机制解方面的帮助,同时对Wessel和Smith表示衷心的感谢。
| [1] | Gan Weijun, Zhang Rui, Zhang Yong, et al. Development of the Crustal Movement Observation Network in China and Its Applications[J]. Recent Developments in World Seismology,2007(7):43-52(甘卫军,张锐,张勇,等.中国地壳运动观测网络的建设及应用[J]. 国际地震动态, 2007(7): 43-52) |
| [2] | Xu Caijun, Dong Lixiang, Shi Chuang, et al.A Study on Annual Accumulation of Strain Energy Density Significance by Using GPS Measurements in North China[J]. Chinese Journal of Geophysics,2002,45(4):497-506(许才军,董立祥,施闯,等.华北地区GPS地壳应变能密度变化率场及其构造运动分析[J]. 地球物理学报, 2002,45(4): 497-506) |
| [3] | Chen Zu'an, Bai Wuming, Lin Banghui, et al.Numerical Simulation for Rupture Processes of a Series of Strong Earthquakes(Ms>7) in North China Since 1966[J].Chinese Journal of Geophysics,2003,46(3):373-381(陈祖安,白武明,林邦慧,等. 1966年以来华北地区一系列七级大震破裂过程的数值模拟[J]. 地球物理学报, 2003,46(3): 373-381) |
| [4] | Guo Liangqian, Bo Wanju, Yang Guohua,et al.Characteristics of Horizontal Deformation Strain Field in North China from 1999 to 2009[J].Journal of Geodesy and Geodynamics,2011,31(3):15-19(郭良迁,薄万举, 杨国华,等.华北1999-2009年水平形变应变场特征[J]. 大地测量与地球动力学, 2011,31(3): 15-19) |
| [5] | Huang Liren, Ma Qing, Guo Liangqian, et al. Dynamic Mechanism for Horizontal Deformation in Part of North China Area—Three-Dimensional Finite-Element Calculation and Analysis of Results from GPS Remeasurement[J]. Acta Sensmologica Sinica,1999,21(1):51-57(黄立人,马青,郭良迁,等. 华北部分地区水平变形的力学机制——三维有限单元计算和GPS复测结果的分析[J]. 地震学报, 1999,21(1): 51-57) |
| [6] | Jia Shixu,Zhang Xiankang. Crustal Structure and Comparison of Different Tectonic Blocks in North China[J]. Chinese Journal of Geophysics,2005,48(3):611-620(嘉世旭,张先康.华北不同构造块体地壳结构及其对比研究[J]. 地球物理学报, 2005,48(3): 611-620) |
| [7] | Jiang Zaisen, Zhang Xi, Chen Bing,et al.Characteristics of Recent Horizontal Movement and Strain-Stress Field in the Crust of North China[J].Chinese Journal of Geophysics,2000,43(5):657-665(江在森,张希,陈兵,等. 华北地区近期地壳水平运动与应力应变场特征[J]. 地球物理学报, 2000,43(5): 657-665) |
| [8] | Liu Xia, Ma Jin, Fu Rongshan, et al. The Primary Research of Crustal Movement Dynamics in Current North China[J]. Chinese Journal of Geophysics,2010,53(6):1 418-1 427(刘峡,马瑾,傅容珊,等.华北地区现今地壳运动动力学初步研究[J]. 地球物理学报, 2010,53(6): 1 418-1 427) |
| [9] | Yang Guohua, Xie Juemin,Han Yueping.Current Horizontal Deformation and Kinematic Mechanism of Major Tectonic Units and Boundary Zones in North China[J].Chinese Journal of Geophysic,2001,44(5):645-653(杨国华,谢觉民,韩月萍.华北主要构造单元及边界带现今水平形变与运动机制[J]. 地球物理学报, 2001,44(5): 645-653) |
| [10] | Zhang Yuegang,Hu Xinkang. Relative Motion Between Plates and Their Boundaries in North China[J]. Journal of Geodesy and Geodynamics,2005,25(1):47-50(张跃刚,胡新康.华北地区块体及其边界的相对运动[J]. 大地测量与地球动力学, 2005,25(1): 47-50) |
| [11] | Tang Fangtou. A Study on the Characteristics of Recent Tectonic Deformation and Earthquake Activity in North China[D]. Beijing :Institute of Geology, China Earthquake Administration, 2003(唐方头.华北地块近期构造变形和强震活动特征研究[D].北京:中国地震局地质研究所,2003) |
| [12] | Yang Guohua, Yang Bo, Chen Xin,et al.The Basic Characteristics of Spatial Variation of 3D Deformation Field in Current North China[J].Geomatics and Information Science of Wuhan University, 2013,38(1): 31-35 (杨国华,杨博,陈欣,等.华北现今三维形变场空间变化的基本特征[J]. 武汉大学学报·信息科学版, 2013,38(1): 31-35) |
| [13] | Wang Q, Zhang P Z,Freymueller J T, et al. Present-day Crustal Deformation in China Constrained by Global Positioning System Measurements[J]. Science, 2001,294(5 542): 574-577 |
| [14] | Wu Yanqiang, Jiang Zaisen, Yang Guohua,et al. Application and Method of GPS Strain Calculating in Whole Mode Using Multi-Surface Function[J].Geomatics and Information Science of Wuhan University,2009,34(9):1 085-1 089(武艳强,江在森,杨国华,等.利用多面函数整体求解GPS应变场的方法及应用[J]. 武汉大学学报·信息科学版, 2009,34(9): 1 085-1 089) |
| [15] | Ekström G, Nettles M, Dziewoński A M.The Global CMT Project 2004-2010: Centroid-Moment Tensors for 13017 Earthquakes[J]. Physics of the Earth and Planetary Interiors, 2012, 200/201: 1-9 |
| [16] | Deng Qidong, Zhang Peizhen, Ran Yongkang, et al. The Basic Characteristics of Active Tectonics in China[J]. Science in China(Series D),2002,32(12):1 020-1 030(邓起东,张培震,冉勇康,等. 中国活动构造基本特征[J]. 中国科学D辑:地球科学, 2002,32(12): 1 020-1 030) |
| [17] | Deng Qidong, Zhang Peizhen, Ran Yongkang, et al. Active Tectonics and Earthquake Activities in China[J]. Earth Science Fronties,2003,10(Suppl):66-73(邓起东,张培震,冉勇康,等.中国活动构造与地震活动[J]. 地学前缘, 2003,10(特刊): 66-73) |
| [18] | Hardy R L. Theory and Applications of the Multiquadric-Biharmonic Method[J]. Computers Math Applic, 1990,19(8/9): 163-208 |
| [19] | Yao Yibin, Liu Qiang, Peng Wenfei,et al. A New MQ-B Method Suitable for Large Scale Velocity Field Modeling[J].Geomatics and Information Science of Wuhan University, 2012,37(10): 1 155-1 159(姚宜斌,刘强,彭文飞,等. 适用于大尺度速度场建模的MQ-B新模型[J]. 武汉大学学报·信息科学版, 2012,37(10): 1 155-1 159) |
| [20] | Wu Y Q, Jiang Z S,Yang G H,et al. Comparison of GPS Strain Rate Computing Methods and Their Reliability[J]. Geophysical Journal International, 2011,185(2): 703-717 |
| [21] | Savage J C, Gan W J,Svarc J L.Strain Accumulation and Rotation in the Eastern California Shear Zone[J]. Journal of Geophysical Research—Solid Earth, 2001, 106(B10): 21 995-22 007 |
| [22] | Shi Yaolin,Zhu Shoubiao.Discussion Method of Calculating Strain with GPS Displacement Data[J]. Journal of Geodesy and Geodynamics,2006,26(1):1-8(石耀霖,朱守彪.用GPS位移资料计算应变方法的讨论[J]. 大地测量与地球动力学, 2006,26(1): 1-8) |
| [23] | Yang Guohua, Jiang Zaisen, Wang Min,et al.Effect of Indonesta Earthquake on Horizontal Crustal Movement in Sichuan-Yunnan Region[J].Journal of Geodesy and Geodynamics,2006,26(1):6-14,20(杨国华,江在森,王敏,等. 印尼地震对我国川滇地区地壳水平活动的影响[J]. 大地测量与地球动力学, 2006, 26(1): 9-14,20) |
| [24] | Yang bo, Zhang Fengshuang, Zhan Wei,et al.Experiment for Filtering Horizontal Movement Field and Its Strain Calculation[J].Jouranl of Geodesy and Geodynamics,2010,30(5):106-112(杨博,张风霜,占伟,等. 水平运动场滤波试验与应变计算[J]. 大地测量与地球动力学, 2010,30(5): 106-112) |
 2015, Vol. 40
2015, Vol. 40


