文章信息
- 吴华意, 李锐, 周振, 蒋捷, 桂志鹏
- WU Huayi, LI Rui, ZHOU Zhen, JIANG Jie, GUI Zhipeng
- 公共地图服务的群体用户访问行为时序特征模型及预测
- Research and Prediction on Time-Sequence Characteristics of Group-User Access Behavior in Public Map Service
- 武汉大学学报·信息科学版, 2015, 40(10): 1279-1286,1316
- Geomatics and Information Science of Wuhan University, 2015, 40(10): 1279-1286,1316
- http://dx.doi.org/10.13203/j.whugis20150283
-
文章历史
- 收稿日期: 2015-05-06

2. 地球空间信息技术协同创新中心, 湖北 武汉, 430079;
3. 国家基础地理信息中心, 北京, 100830;
4. 武汉大学遥感信息工程学院, 湖北 武汉, 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. National Geomatics Center of China, Beijing 100830, China;
4. School of Remote Sensing and Information Science, Wuhan University, Wuhan 430079, China
地理空间信息系统向着网络化、规模化、虚拟化、服务化和时空化的方向发展,以Google Maps/Google Earth、World Wind、Bing Map、天地图等为代表的公共地图服务平台为用户带来了全新的体验[1]。随着Internet的快速发展和移动网络的不断普及,公共地图服务用户与日俱增,导致其实时在线操作达到了百万级。高强度的访问及访问的集中性带来了一系列的问题,如服务器过载、访问延迟、通信错误增多等。服务器有限的能力需通过扩展硬件来满足其数据量和用户量日益增长的需要,且其服务维护使用成本逐渐增高。云计算是一种新一代的计算模式,其计算资源的虚拟化可使计算资源按需提供服务,并且可以动态地扩展计算资源。将公共地图服务迁移到云中,可满足其对计算资源日益剧增的需求。但云计算资源的分配方式是按需分配,特别是一些能提供较高服务性能的商业云,将收取一定的资源租赁费用。因此,如何有效地选择和利用云服务资源,控制公共地图服务成本,在投入和质量需求之间到达最佳的平衡点,对于拥有海量用户并对 地理空间信息服务质量有较高要求的公共地图服务来说尤其重要[2, 3, 4, 5]。而此方面的研究多聚集在云服务计算能力和云服务可扩展性评估[6]、云服务资源的地理位置部署[7]、云服务的计费模式[8]、云服务就绪度[9]等方面,极少从云服务支撑的公共地图服务应用的自身特点与需求选择云服务资源。
用户的访问行为直接影响着公共地图服务对计算资源的需求。而海量用户对公共地图服务的访问行为具有社会性,存在着一定的群体模式。通过分析和挖掘群体用户的访问行为模式,可针对性地解决服务质量与服务成本的相关性问题[10]。且公共地图服务拥有大量的日志数据,提供了丰富的用户动态行为信息。近期,不断有研究人员利用不同的公共地图服务日志数据进行用户访问行为的统计分析与仿真,以期建立合适的用户访问模型。并且许多研究学者认为研究和挖掘大规模用户在地理信息服务系统中漫游时所表现出来的社会学规律和交互模式,为系统的性能优化、提高用户漫游流畅体验提供非常重要的指引作用[11]。Fisher[12]和Talagala[13]分别对地理信息的访问请求频率进行统计,提出数字地球中影像数据的访问请求服从社会学中的幂律分布。王浩等[14]通过实验分析扩展了其结论,得出影像数据瓦片请求符合幂律分布中的Zipf\|like分布。幂律分布全局地反映了地理信息访问中的一种时间长期累积访问特征,但不能实时反映用户访问模式的变化。Park等[15]认为,用户的访问模式取决于地理数据的空间位置性。Yang等[16]提出用户访问公共地图服务平台时带给服务器的负载具有潮汐特征。这些都说明了因地理数据存在时空属性,所以用户的访问请求同样存在时空聚集性。此访问特性对服务负载,如流量波动、服务队列长度等公共地图服务性能产生了重要的影响,同时也决定着公共地图服务对计算资源的需求。与此同时,公共地图服务中用户的访问到达在时间上是随机的。因此,如何有效地表达和捕捉用户访问的聚集性及其访问强度随时间的变化,进行准确、快速的服务负载预测,解决由于用户访问的集中性和突发性所带来的服务器性能问题,是其难点与根本。本文分析了大量的非结构化的用户访问公共地图服务历史记录,基于时间序列聚类方法发现群体用户访问强度随时间变化的规律;利用 群体用户访问强度具有多峰值、变强度以及周期性的特点,将用户访问到达率的时间序列分割成若干个相对较短但不重叠的子序列访问模式区间,更精确地匹配群体用户访问在时间上的聚集性和突发性特征;并对各个时序区间分别预测访问负载,提高预测准确度的同时,实现一种简单有效且只需少量的先验历史数据的负载预测方法。此方法可用于指导公共地图服务资源的需求和规划,以提高资源的利用效率,并满足用户对公共地图服务质量的需求。
1 群体用户访问行为的时序建模若将一个用户访问公共地图服务的请求到达看成一个随机点,则这是一个源源不断出现的随机过程。在这过程中,任一时间段内达到的用户请求数也是随机的,为公共地图服务带来随机的访问强度与负载。单位时间内平均到达的用户请求数可称为公共地图服务的访问到达率λ,而群体用户访问公共地图服务的访问强度通常可用访问到达率来表达,且可用于公共地图服务中服务器负载的预测,它属于时间序列预测的范畴。对于访问量稳定的网络系统,呈现单峰值特征,可使用回归分析、灰度预测、拓扑预测、线性网络预测、BP神经网络预测、Karkov等方法预测用户访问行为的趋势。而对于类似公共地图服务的网络系统,群体用户的访问在时序上呈现非均质特征,用户到达率所构成的时间序列具有多峰值和周期性。因此,需针对群体用户访问特征,阶段性、周期性地建立准确的访问负载预测模型。同时也需考虑应对群体用户密集访问的预测方法对公共地图服务系统资源占用最小,保证预测精度高的同时,算法时间复杂度小。
1.1 样本数据及预处理本文采用公共地理信息服务平台天地图服务器端采集的用户访问日志数据作为本文研究的基础数据。天地图是国家测绘地理信息局建设的地理信息综合服务网站。它是数字中国的重要组成部分,是国家地理信息公共服务平台的公众版。访问该网站的用户具有广域的地域性,日志数据以非结构化形式记录在不同的集群服务器和不同的文件中。选取的样本数据集为2014年2月海量用户访问的日志文件,数据存于上百个文件中,每日文件大小为20 G。本文建立MongoDB分布式文件存储的数据库,基于MapReduce并行计算框架对数据进行格式化处理,建立高效的索引和存储,形成每日近9千万条数据,包括时间、用户IP、请求的数据经纬度、层数、数据来源等。因天地图的访问中存在人类用户(普通的访问用户)和机器用户(程序下载数据资源用户),为了真实可靠地反映人类用户的群体行为,在数据预处理中根据机器用户的特征,如单个用户访问量巨大,或单个用户连续爬取一定经纬度范围的数据,或连续大量访问某个区域数据等,剔除了机器用户的访问记录。为了保证时序分析在时间上和访问特征聚类的精确度,以10 min为间隔,统计天地图用户访问的平均到达率用于样本分析。
1.2 群体用户访问的时序分布模型对于公共地图服务平台而言,用户访问行为具有一定的模式性,即在不同的时间区间,用户到达率λ的值是变化的。从时间序列的角度分析,若将一个周期的时间分为若干等长时段,每个时段的请求数可以构成一个时间序列L(S,t):
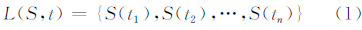
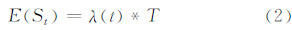
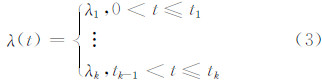
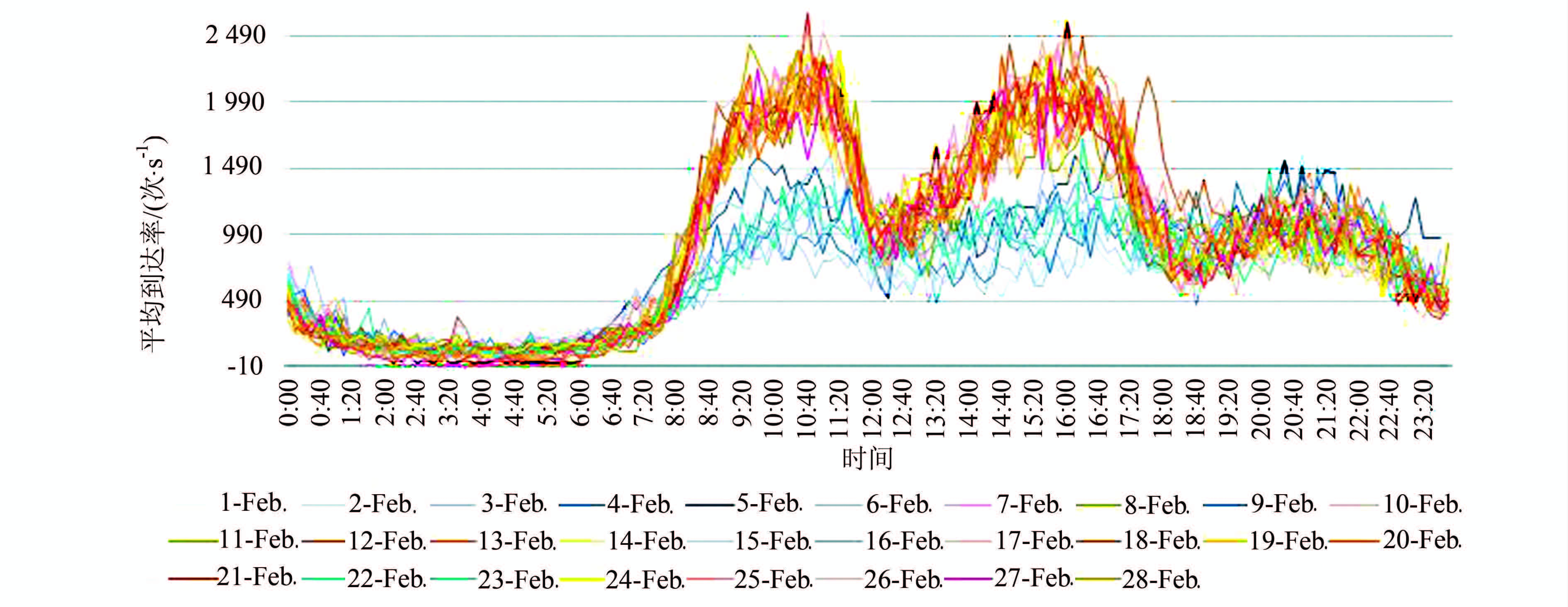
依据上述群体用户访问的时序方法,为样本数据建立访问平均到达率λ(t)的时序分析图。图 1是统计样本数据后得到的2014年2月1日到2月28日的平均到达率变化图。从图 1可以看出,公共地图服务平台每天的用户到达率λ(t)的时序变化规律相似,且以天为周期单位。在这种周期分类上,用户工作日(暖色曲线)的访问行为模式与节假日(冷色曲线)的访问行为模式不同,体现在白日时间的高峰期访问到达率明显不同。因此,可先粗略地将用户的访问行为分为工作日模式与节假日模式。
|
| 图 1 工作日与节假日用户到达率变化情况 Fig. 1 User Arrival Rate in Working Days and Holidays |
图 1显示出在一个周期内,群体用户访问到达率分布曲线在不同的时间段也呈现出不同的分布模式,其访问到达率的分布具有明显的区别。因此,若要实现群体用户访问行为的精确预测,则需对工作日模式与节假日模式进行进一步时序聚类划分,如式(3)所示。
1.3 群体用户访问到达率时间序列的最优分割若要利用群体用户访问的模式性及周期性进行公共地图服务负载预测,首先需分割和挖掘群体用户到达率在时间序列中不同的访问模式,以获得式(3)中各访问模式的时间区间ti。研究可知,对群体用户访问到达率聚类是模式分割的有效方法。图 1显示出群体用户访问模式在时间上是连续的,因此本文基于Fisher最优分割方法进行有序聚类,进而有效地发现用户访问到达率在时间序列上的模式区间,即对一个周期的时间序列 L(S,t)进行合理的划分,得到不同访问模式所在的时间区间集合T= T1,T2,…,Tk 。
Fisher最优分割算法的思想是:当数据按一定的时间顺序排列,为了探索事物发展的周期性或旋回性,并合理地划分呈现不同模式的阶段,则需要进行最优分割。将一定数量的、规律性的、接近的若干相邻数据归为一个阶段;而相邻两个阶段的数据呈现的模式出现明显的差异,前一个阶段的最后一项数据与下一阶段的头条数据之间便为模式分割的界限。
本文研究需要从用户到达时间序列 L(S,t)中发现用户访问的模式T= T1,T2,…,Tk ,各模式Ti(1≤i≤k)在时间上相邻接,但用户平均到达率λ(ti) 却不同,且各模式适用于群体用户访问周期变化。图 1显示,公共地图服务用户在工作日与节假日的访问模式明显不同,所以对此模式的分割与模式挖掘分为工作日模式与节假日模式。
本文以工作日模式为例,建立多变量的、有序的表达方法实现群体用户访问到达率的最优分割。其中,因短时间内的访问到达率相似,以每10 min为时间间隔聚类得到一个周期内144个平均到达率,建立有序的访问到达率时间序列表达,如式(4)所示。将2014年2月1日至2月21日工作日的访问到达率作为训练样本集,如表 1所示。
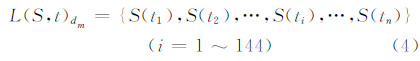
| 时间段 | t | d 2.7 | d 2 .8 | … | D 2.20 | D 2.21 |
| 0:00~0:10 | t 1 | 204 | 268 | … | 521 | 424 |
| 0:10~0:20 | t 2 | 207 | 192 | … | 454 | 304 |
| 0:20~0:30 | t 3 | 162 | 258 | … | 263 | 234 |
| | | | | | | |
| 15:20~15:30 | t 93 | 2 187 | 1 925 | … | 1 840 | 2 288 |
| 15:30~15:40 | t 94 | 2 072 | 1 598 | … | 1 993 | 2 183 |
| | | | | | | |
| 23:40~23:50 | t 143 | 306 | 358 | … | 600 | 420 |
| 23:50~24:00 | t 144 | 440 | 419 | … | 505 | 492 |
将式(4)展开形成多个周期内访问到达率时间序列的平均到达率矩阵:
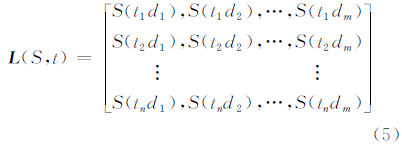
基于Fisher最优分割法对矩阵 L (S,t)进行最优分割[17],将值相似且相邻的行向量(访问到达率向量) S(ti),S(ti+1),…,S(tn)聚为一类,形成K类访问模式以及各模式所在的时间区间集合 T1,T2,…,Tk 。方法与步骤如下。
1) 计算访问到达率向量的直径
设分割后访问到达率向量的某一访问模式包含时序{S(i),S(i+1),…,S(j)}={S(ti),S(ti+1),…,S(tj)} j>i ,记为G= i,i+1,…,j ,则该访问模式的向量均值 G为:
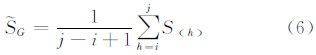
设模式内访问到达率向量的直径为访问到达率向量集的离差平方和D i,j ,则有:
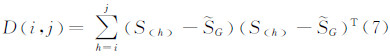
2) 计算访问到达率向量分割损失函数
设b( n,K )为将有序的n个访问到达率向量被分割成K个访问模式的一种分类方法,则b( n,K ) 可表达为:
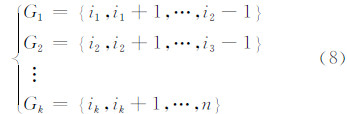
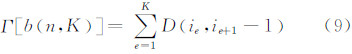
当n、K固定时,Γ [b (n,K)]越小,即各类模式的离差平方和越小,则模式的分类是合理的。因此在此寻找一种合适的b( n,K ),使其损失函数值Γ最小。
记P (n,K) 为使Γ达到最小的分类方法。利用递推式(10)求出K取不同值时,各分类方法的最小损失函数以及各模式之间的分割点:
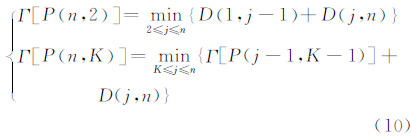
3) 计算访问到达率向量分割的最优解
若访问到达率向量分割的次数K( 1<K<n )已知,求使损失函数值最小的分割方法P (n,K) 。 首先寻求分割点jk,使其满足:
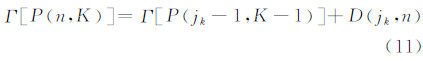
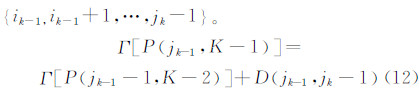
根据递推式(10)可以得到所有类G1,G2,…,Gk,则所求的最优分割方法为:
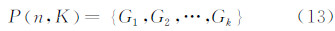
如此计算得出在K次分割下,各个模式中时间序列的分割点 {j1,j2,…,jk }。
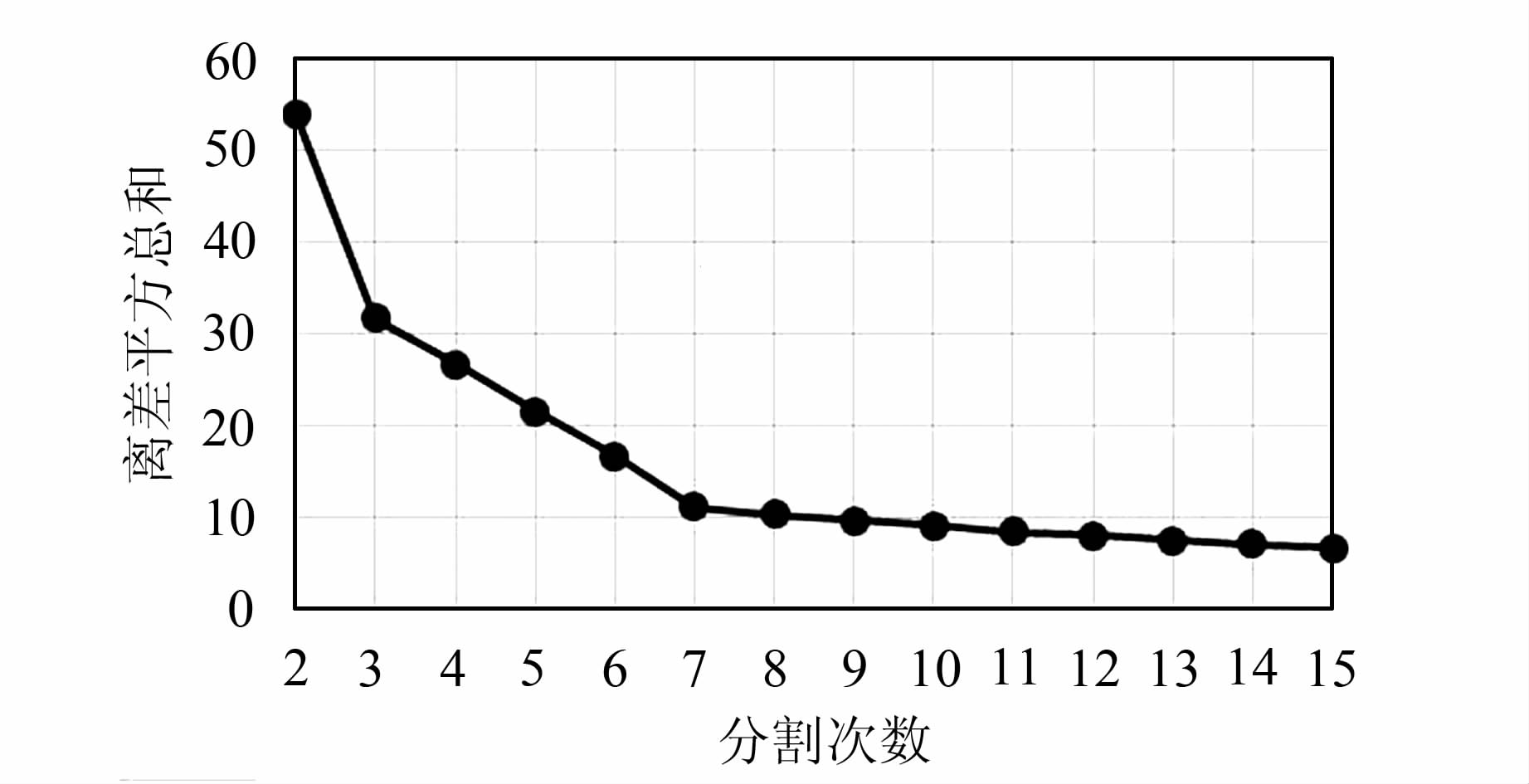
训练实验中,对训练样本中的访问到达率数据进行2~15次最优分割,分别得到各次分割下的最小损失函数值,如图 2所示。
|
| 图 2 最小损失函数值变化图 Fig. 2 Variation of Minimum Loss Function Value |
K值的确定依据Fisher原理:在Fisher最优分割过程中,最小损失函数值Γ随分割数K的增加而减少。而当分割数增加到某一数值后,最小损失函数值曲线将急剧变缓,达到一定的平衡,此时的K值为最佳分割值。本文基于非负斜率方法确定K值,如式(14)所示:
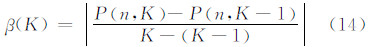
当β(K)较大时,表示分K类优于分K-1类;当β(K)接近于0时,此时K为合适的取值。由图 2与式(14)可计算出K=7时为最佳分割取值。且本文对访问到达规律的研究是为了准确且简单有效地预测公共地图服务的访问负载。若群体用户访问到达率在一个周期内的时序访问模式区间过多,则预测所需的先验数据量越大,预测的复杂度及所需的计算存储容量也将随之递增;模式区间过少,则影响预测精度。因此,综合考虑最优分割原理与访问负载预测的可行性,分割方法P( n,7 )是合适的。本文在实验中通过训练样本集得到了各访问模式所在时间区间的集合 T1,T2,…,T7 ,如表 2所示。表 2显示,K值为7时,各访问模式的离差平方和值较小。
| T k | 时间段 | 访问模式离差平方和 |
| T 1 | 01:10~07:50 | 2.027 1 |
| T 2 | 07:50~08:50 | 0.677 6 |
| T 3 | 08:50~11:40 | 2.189 8 |
| T 4 | 11:40~14:10 | 1.502 4 |
| T 5 | 14:10~17:30 | 2.231 5 |
| T 6 | 17:30~23:00 | 2.007 1 |
| T 7 | 23:00~01:10 | 0.557 8 |
群体用户访问到达率变化的周期性及模式性为访问到达率的预测提供了可靠的条件。§1.3中对群体用户访问达到率时序的最优分割可以很好地对不同时段内具有不同强度特征的访问达到率进行有效的划分,是实现准确预测访问负载的基础。而在此之上挖掘不同时间序列模式下的访问到达率的概率分布是准确预测访问负载的关键。本节为不同时序下的访问到达模式建立了一种累积概率分布,表达该模式下的访问到达概率密度的分布;并基于不同访问模式下的累积概率分布和基于时间序列平滑预测方法,对不同访问模式下的访问负载进行预测,实现基于少量的先验历史数据即可快速准确地预测。
定义1 访问到达率的累积概率分布函数为访问到达率概率密度函数的积分,即为访问到达率小于或等于某个数值的概率。本文根据§1.3得出的用户访问行为模式时序的划分方法,对不同访问模式下的用户到达率分布进行累积概率分布分析。各模式下的访问到达率的累积概率分布函数为:
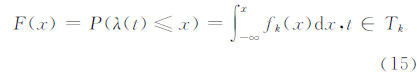
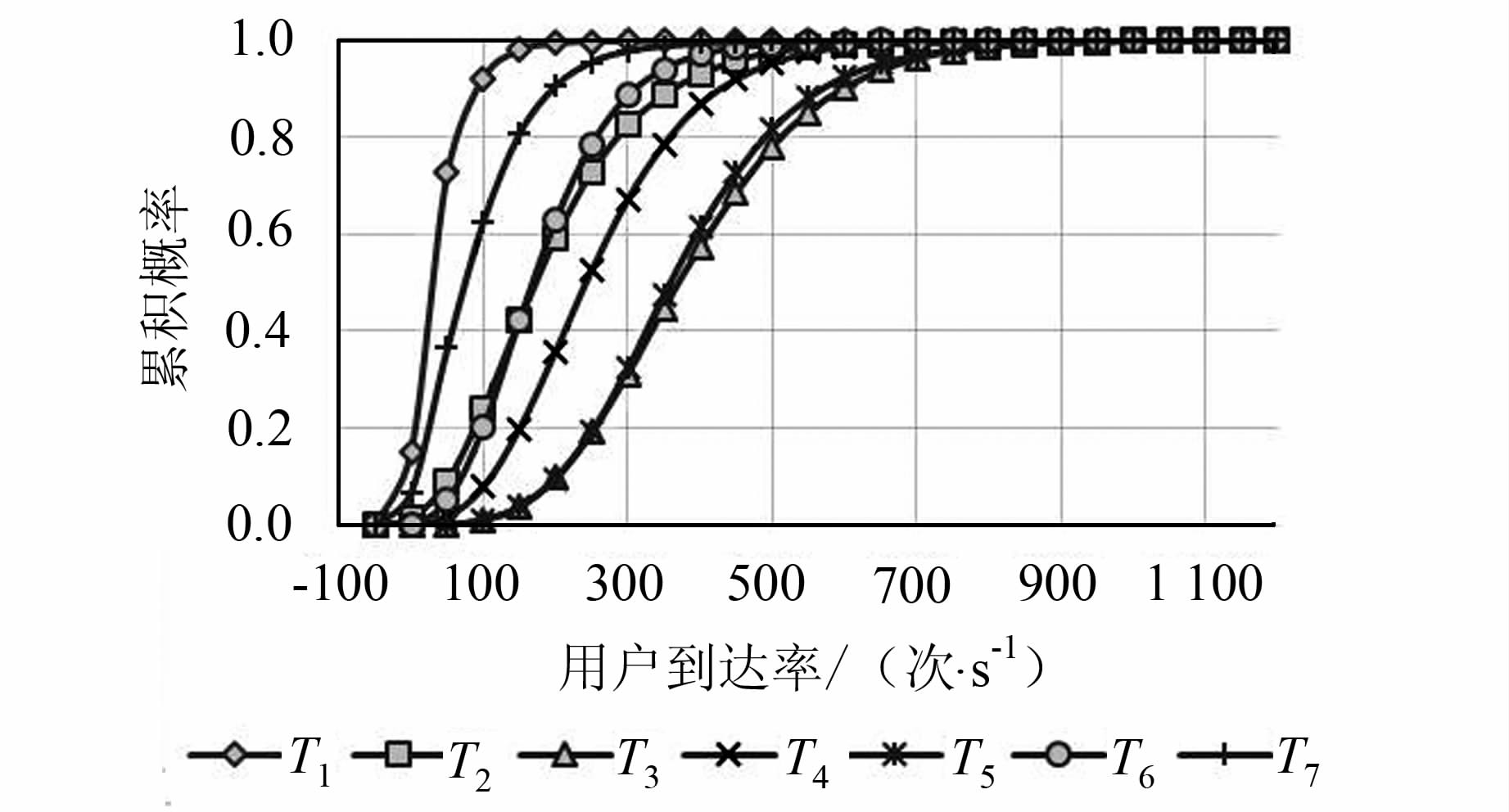
根据式(15),当t∈Tk(k=1,…,7)时,用户到达率λ(t)≤x的概率为P(λ(t)≤x)。各模式访问到达率的累积概率分布如图 3所示。
|
| 图 3 各模式访问到达率的累积概率分布 Fig. 3 Cumulative Probability Distribution of the Access Arrival Rate |
访问到达率的预测是为了寻求不同时间区间的访问峰值,更好地进行云计算资源的利用与分配。在此,令F(x)=0.99,可以求得不同访问模式下的访问到达率峰值λk,t∈Tk( k=1,…,7),即当t∈Tk时,λ(t)≤λk的概率为0.99。λk可以用于衡量Tk访问模式区间内群体用户的访问强度与负载。
定义一个周期du内不同访问模式下的用户访问到达率参数λk为:
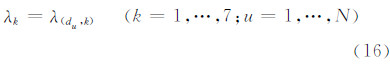
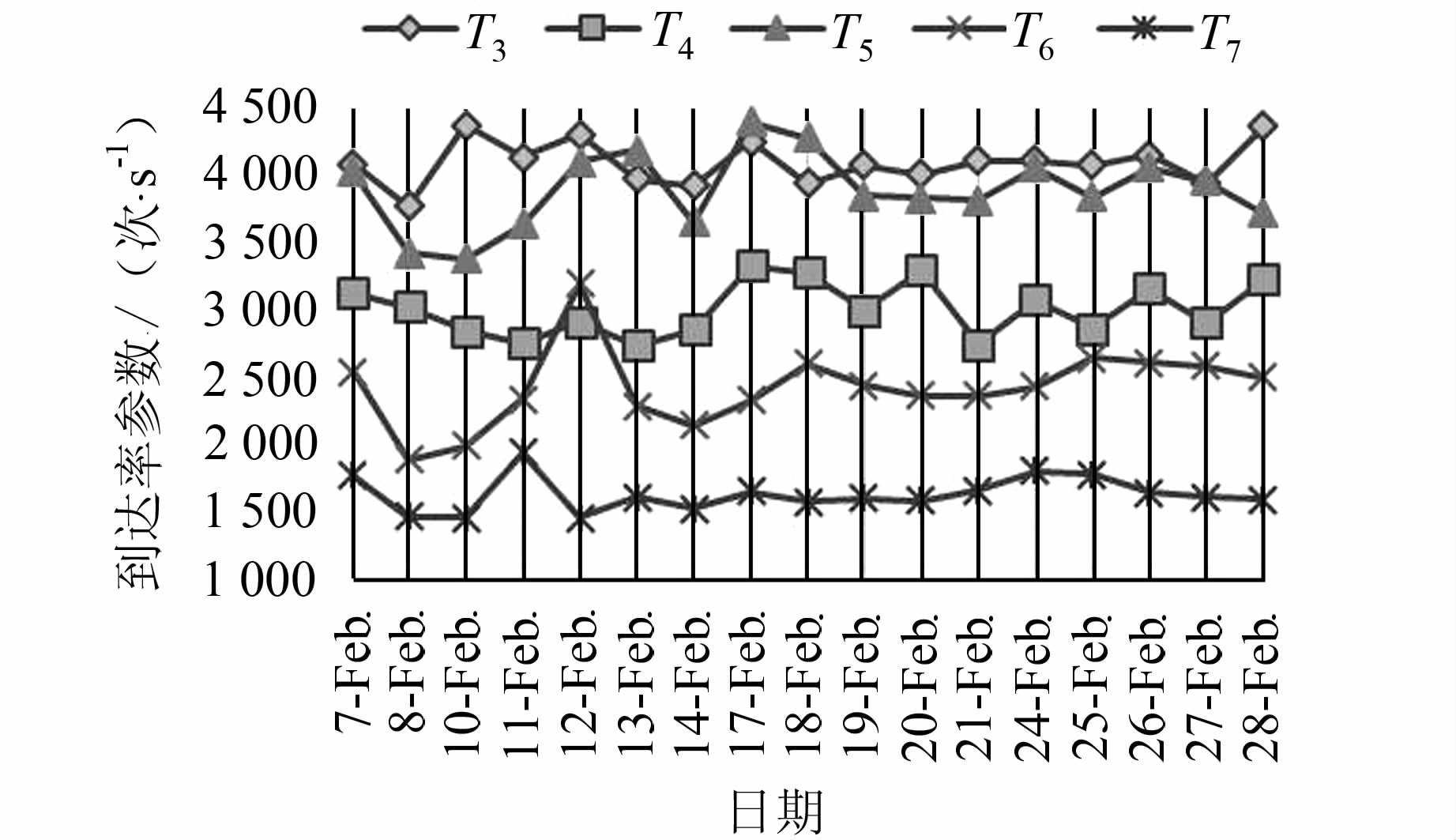
根据式(16),对样本数据工作日访问到达率进行分模式累积概率分布分析,得到λk的时序分布如图 4所示。
|
| 图 4 工作日分模式下的到达率参数时序分布 Fig. 4 Variation of Arrival Rate Parameters in Working Days |
从图 4可以看出,各周期同一访问模式下的到达率参数λk波动较小,有一定的相关性和稳定性。说明§1.3中访问模式的分割适应并匹配周期的变化体现了群体用户访问的一种周期性的规律。基于λk的这种相对稳定的变化,可以对λk进行平滑预测。
2.2 群体用户访问负载的平滑预测群体用户访问量变化的规律具有周期性,且同一访问模式下访问到达率参数的分布具有一定的稳定性。根据此群体用户的访问特性,本文基于一次移动平均法对用户的访问到达率参数λk进行预测。
预测方法的思想为:对同一周期内的不同访问模式Tk分别预测。收集各访问模式N个周期的观察值,即N个周期内Tk模式访问到达率参数λ(du,k),计算该组观察值的均值,利用这一均值预测下一周期该访问模式下的访问到达率。
移动平均法有两种极端情况:① 在移动平均 值的计算中包括过去观察值的实际个数N=1,此时利用最新的观察值作为下一期的预测值;② N=N′,这时利用全部N′个观察值的算术平均值作为预测值。
当数据的随机因素较大时,宜选用较大的N,较大限度地平滑由随机性所带来的严重偏差;反之,当数据的随机因素较小时,宜选用较小的N,这有利于跟踪数据的变化,并且预测值滞后的期数也少。
设到达率参数时间序列为λ(d1,k),λ(d2,k),…,λ(dN,k),则对周期dN+1的Tk模式访问到达率参数λ(dN+1,k)移动平均法预测可以表示为:
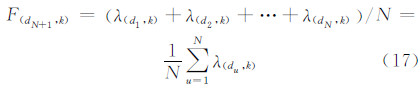
由移动平均法计算公式可以看出,每一新预测值是对前一移动平均预测值的修正,N越大,平滑效果越好。
该预测方法的优点是计算量小,其计算复杂度为O(1),且移动平均能较好地反映时间序列的趋势及其变化。其缺点是计算移动平均值必须具有N个过去观察值,当N较大或时序访问模式个数K值较大时,计算过程中需要使用大量的先验数据,这些都需要大量的计算资源和存储资源。本文提出的最优分割中,K值为7,使用的先验数据量相对很小。因此,群体用户访问负载的平滑预测方法是否会增加系统的消耗取决于N值。
2.3 预测结果分析基于2014年2月所有工作日的用户访问日志数据,对各访问模式下的访问到达率进行预测,取N=2,…,10。预测准确率和均方误差如表 3所示。
| N | T 1 | T 2 | T 3 | T 4 | T 5 | T 6 | T7 | |||||||
| 准确率/% | 均方误差 | 准确率/% | 均方误差 | 准确率/% | 均方误差 | 准确率/% | 均方误差 | 准确率/% | 均方误差 | 准确率/% | 均方误差 | 准确率/% | 均方误差 | |
| 2 | 89.33 | 4.62 | 92.26 | 9.92 | 96.37 | 7.81 | 93.77 | 9.21 | 92.80 | 13.13 | 88.79 | 14.97 | 93.07 | 6.61 |
| 3 | 90.55 | 4.63 | 93.14 | 10.00 | 96.74 | 6.58 | 93.32 | 9.73 | 93.42 | 12.13 | 89.47 | 14.50 | 93.16 | 5.80 |
| 4 | 92.31 | 3.64 | 93.88 | 9.95 | 96.71 | 6.52 | 93.90 | 9.73 | 93.44 | 12.03 | 92.13 | 12.42 | 95.15 | 4.16 |
| 5 | 92.70 | 3.46 | 92.95 | 9.85 | 97.36 | 5.46 | 92.76 | 10.51 | 94.08 | 11.31 | 96.24 | 4.59 | 95.60 | 3.54 |
| 6 | 92.40 | 3.60 | 93.66 | 9.46 | 96.99 | 6.03 | 93.12 | 10.09 | 94.13 | 11.30 | 95.57 | 5.46 | 95.33 | 3.72 |
| 7 | 93.39 | 3.25 | 94.01 | 9.72 | 97.34 | 5.43 | 92.73 | 10.15 | 94.72 | 11.09 | 95.26 | 5.89 | 95.70 | 3.73 |
| 8 | 94.21 | 3.11 | 93.27 | 10.32 | 97.48 | 5.54 | 93.78 | 8.57 | 96.17 | 7.68 | 94.79 | 6.20 | 95.77 | 3.89 |
| 9 | 94.22 | 3.12 | 92.77 | 10.96 | 98.03 | 4.90 | 94.62 | 7.39 | 97.32 | 5.40 | 96.35 | 4.62 | 95.93 | 3.84 |
| 10 | 93.56 | 3.32 | 92.94 | 11.21 | 97.78 | 5.29 | 94.04 | 7.72 | 97.24 | 5.21 | 96.65 | 4.40 | 95.2 | 4.02 |
基于本文提出的方法进行访问负载预测时,移动的项数N越大,对原数列波动的曲线修匀得越光滑,便越能显示出各个访问模式下访问负载的一种周期性发展趋势,但N越大,所需的先验数据越多,系统消耗也越大。综合预测准确率和均方误差值,N=9时,平滑预测效果较好,预测准确率较高,在92.77~98.03之间,即N=9时即可体现出群体用户访问的周期性规律。这进一步说明了本文提出的基于时序的访问模式分割能准确地体现访问强度变化的规律性和区间性,是公共地图服务中访问负载预测准确率较高,且需要少量的预测先验数据的关键和基础。
2.4 群体用户访问负载模型应用的可行性验证群体用户访问达到率决定着公共地图服务平台承受的负载,影响着其资源需求和云中资源分配,对云的弹性服务研究具有指导意义[18, 19]。基于上述建立的时间序列的访问负载时序模型与预测方法,在云仿真平台Cloudsim上初步验证了群体用户访问负载预测方法应用于云计算资源分配的可行性与有效性。实验中采用日志驱动仿真实验,用离散事件模拟机制实现用户的访问及其对访问请求的处理。云中单台虚拟机计算资源的配置如下:型号为IBM System X,CPU个数为2个,CPU主频为2.6 G,核心为4,内存64 G,硬盘2 T,平均响应时间0.02 s。其中云任务量为预测的2014年2月28日用户访问到达率的分段模式,公共地图服务平台负载均衡上采用轮询方式将计算资源赋予处理用户访问的请求,所有的用户共用1个数据中心。因公共地图服务用户在地 图中浏览时,若需要保证较好的漫游体验,响应时间则不超过0.02 s[20]。因此实验中以平均响应时间0.02 s为性能目标,寻求在不同时间段访问强度下所需的计算资源的临界值,即虚拟机个数,如表 4所示。由此可见,针对不同周期/时段预测的访问强度,云服务商可为公共地图服务平台进行有效的、合适的资源分配,比如计算资源、存储资源、网络带宽等分配,保证公共地图服务质量的同时,高效地按需使用云服务资源,实现云的弹性服务。
| T k | 时间段 | 到达率/s | 服务器个数/个 |
| T 1 | 01:10~07:50 | 914 | 2 |
| T 2 | 07:50~08:50 | 2 825 | 6 |
| T 3 | 08:50~11:40 | 4 100 | 9 |
| T 4 | 11:40~14:10 | 3 007 | 7 |
| T 5 | 14:10~17:30 | 3 897 | 8 |
| T 6 | 17:30~23:00 | 2 413 | 5 |
| T 7 | 23:00~01:10 | 1 625 | 4 |
公共地图服务的群体用户访问具有周期性、时序性和聚集性,此特征有利于其服务性能和系统资源分配的优化。本文建立了公共地图服务中群体用户访问行为的时序分布模型,体现出群体用户并发访问的多峰值变强度特征;并基于此模型提出一种准确且简单有效的、阶段性的时序区间模式预测群体用户访问负载的方法。该预测方法依据群体用户访问的聚集性与周期性,并经过验证可较好地满足公共地图服务中群体用户并发访问的性能需求,从而用于云计算资源分配的优化。今后可结合群体用户访问的地域性和时序性,进一步探究群体用户访问中精确的时空规律,结合云资源的时空表达及公共地图服务性能的表达方法,建立精确、高效的云资源时空分配策略。
致谢:感谢国家基础地理信息中心和公共地理信息服务平台天地图提供的帮助与支持。
| [1] | Li Deren,Sui Haigang,Shan Jie,et al. Discussion on Key Technologies of Geographic National Conditions Monitoring[J].Geomatics and Information Science of Wuhan University, 2012, 37(5):505-512(李德仁, 眭海刚, 单杰, 等.论地理国情监测的技术支撑[J].武汉大学学报·信息科学版, 2012, 37(5):505-512) |
| [2] | Wu Huayi,Zhang Hanwu. QoGIS: Concept and Research Framework[J]. Geomatics and Information Science of Wuhan University,2007,32(5): 385-388(吴华意, 章汉武. 地理信息服务质量(QoGIS):概念和研究框架[J]. 武汉大学学报·信息科学版,2007,32(5): 385-388) |
| [3] | Zhang Hanwu, Wu Huayi, Hu Yueming, et al. From Quality of Geospatial Data to Quality of Geospatial Information Services[J]. Geomatics and Information Science of Wuhan University,2010,35(9): 1 104-1 107(章汉武, 吴华意, 胡月明, 等. 从地理空间数据质量到地理空间信息服务质量[J]. 武汉大学学报·信息科学版,2010,35(9): 1 104-1 107) |
| [4] | Gong J,Wu H,Zhang T,et al. Geospatial Service Web: Towards Integrated Cyberinfrastructure for GIScience[J]. Geo-spatial Information Science,2012,15(2): 73-84 |
| [5] | Li Deren. The Geo-spatial Information Science Mission[J]. Geo-spatial Information Science,2012,15(1): 1-2 |
| [6] | Gao J,Pattabhiraman P,Bai X,et al. SaaS Performance and Scalability Evaluation in Clouds[C]. 2011 IEEE 6th International Symposium on Service Oriented System Engineering (SOSE),Irvine,CA, 2011 |
| [7] | Badger L,Grance T,Patt-Corner R,et al. Cloud Computing Synopsis and Recommendations[S]. U.S. Department of Commerce: NIST Special Publication 800-146,2012 |
| [8] | Wu Jun,Xu Ming. A Comparative Analysis on the Billing Model of Public Cloud Service[J]. Telecommunications Science,2012,28(1): 127-132(吴俊,徐溟. 公有云服务计费模式比较研究[J]. 电信科学,2012,28(1): 127-132) |
| [9] | Furht B,Escalante A. Handbook of Cloud Computing[M]. New York: Springer,2010 |
| [10] | Zhang Bo,Wu Lili,Zhou Min. The Analysis of User Behavior Based on Web Usage Mining[J].Computer Science, 2006, 33(8):213-214(张波,巫莉莉,周敏. 基于Web 使用挖掘的用户行为分析[J]. 计算机科学,2006,33(8): 213-214) |
| [11] | Li R,Guo R,Xu Z,et al. A Prefetching Model Based on Access Popularity for Geospatial Data in a Cluster-based Caching System[J]. International Journal of Geographical Information Science,2012, 26 (10): 1 831-1 844 |
| [12] | Fisher D. Hotmap: Looking at Geographic Attention[J]. IEEE Transactions on Visualization & Computer Graphics,2007,13(6):1 184-1 191 |
| [13] | Talagala N,Asami S,Patterson D,et al. The Art of Massive Storage: A Web Image Archive[J]. Computer,2000, 33(11):22-28 |
| [14] | Wang Hao,Pan Shaoming,Peng Min,et al. Zipf-like Distribution and Its Application Analysis for Image Data Tile Request in Digital Earth[J]. Geomatics and Information Science of Wuhan University,2010, 35 (3):356-359 (王浩, 潘少明, 彭敏, 等. 数字地球中影像数据的Zipf-like访问分布及应用分析[J]. 武汉大学学报·信息科学版, 2010, 35(3):356-359) |
| [15] | Park D J, Kim H J. Prefetch Policies for Large Objects in a Web-enabled GIS Application[J]. Data & Knowledge Engineering,2001, 37(1): 65-84 |
| [16] | Yang Chaowei,Wu Huayi,Huang Qunying,et al. Using Spatial Principles to Optimize Distributed Computing for Enabling the Physical Science Discoveries[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011,108 (14):5 498-5 503 |
| [17] | Wang Binfei. Access Pattern Analysis and Performance Optimization of IP Network Video Service System[D]. Hefei:University of Science and Technology of China,2010(王炳飞. IP 网络视频服务系统访问模式分析和性能优化[D]. 合肥: 中国科学技术大学,2010) |
| [18] | Wu H Y,Li Z L,Zhang H W,et al. Monitoring and Evaluating Web Map Service Resources for Optimizing Map Composition over the Internet to Support Decision Making[J]. Computers and Geosciences,2011, 37(4):485-494 |
| [19] | Li D,Zhang J,Wu H. Spatial Data Quality and Beyond[J]. International Journal of Geographical Information Science,2012,26(12): 2 277-2 290 |
| [20] | Zhang Hanwu,Zhu Xinyan,Zhang Songbo. Response Time in WebGIS Based on Vector Data[J]. Journal of Geomatics,2005,30(2): 25-27(章汉武,朱欣焰,张松波. 基于矢量的 WebGIS 用户响应时间问题的若干研究[J]. 测绘信息与工程,2005,30(2): 25-27) |
 2015, Vol. 40
2015, Vol. 40



