文章信息
- 魏小峰, 耿则勋, 娄博, 宋向
- WEI Xiaofeng, GENG Zexun, LOU Bo, SONG Xiang
- 空间目标三维姿态估计方法
- A 3D Pose Estimation Method for Space Object
- 武汉大学学报·信息科学版, 2015, 40(1): 96-101
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 96-101
- http://dx.doi.org/10.13203/j.whugis20130156
-
文章历史
- 收稿日期:2013-05-20
2. 61175部队, 江苏 南京, 210049
2. Unit 61175, Nanjing 210049, China
空间环境感知(space situational awareness,SSA)的任务之一,就是空间目标监视与跟踪。估计卫星及其部件的三维姿态,是空间目标监视的重要内容,对卫星身份识别、异常行为探测、标定配置验证、任务状态估计、工作模式及指向、卫星感兴趣区域确定等起到非常重要的作用[1]。要完成或实现上述任务,就必须识别或估计空间人造目标、空间碎片以及自然星体的空间位置、形状、旋转速度、表面材料构成等特征参数,必须估计或监测空间飞行器的工作状态和健康状况,以达到对空间目标的监视、跟踪、了解、分类、预警等目的。目前,国内空间环境感知领域的主要工作集中在空间目标探测与识别上,对于如何确定已识别卫星的姿态和方位等外形特征缺乏研究[2, 3]。因此,利用望远镜图像估计卫星三维姿态技术具有重大的理论意义与实际价值。
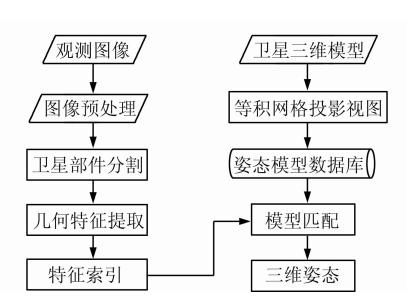
应对这一需求,本文提出了一套完整的估计空间目标三维姿态的理论和方法,主要内容包括多视角姿态模型数据库构造,观测图像预处理、分割和特征提取,特征索引生成与匹配等,最终实现空间目标的三维姿态估计。该方法的整体技术路线如图 1所示。
|
| 图 1 总体技术路线 Fig. 1 Overall Technology Path |
为了有效获取三维空间目标的不同姿态数据,本文采用以目标为中心的多视点投影法,即用不同视点的多个二维投影描述三维空间目标,将获取的目标图像特征与已建立的二维图像模型库中提取出的特征直接匹配。本文使用的三维空间目标模型是由NASA网站给出的Pleiades卫星三维模型,实际应用中也可根据一些已公布的卫星参数来建立。以该三维模型为对象,选择不同视点进行观察,即可得到卫星的二维姿态数据库。
有关投影视图的选择,目前有设置正多面体或等经纬度格网观察球的方法,将三维目标置于坐标轴中心,以正多面体顶点或格网中心位置作为投影视角,获得不同视角即不同姿态的目标图像[4, 5]。但前者受多面体顶点数限制(如八十面体仅有42个顶点),无法得到足够多的姿态数据;后者的不足在于经纬度格网单元的面积变形、形状变形以及内点位置误差随着纬度升高而逐渐递增,这导致不同纬度的相邻观察点与格网中心连线的角度不同,即记录的姿态数据分布不均匀。
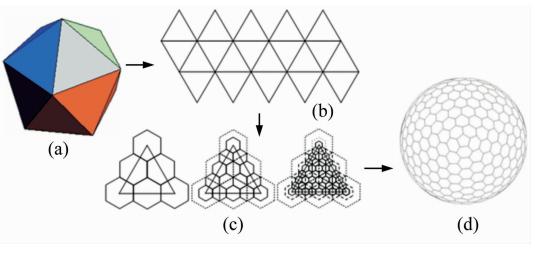
考虑到卫星姿态变化的随机性以及匹配数据库的完整性,任两个相邻观测位置与卫星连线夹角应相同,且相邻观测姿态旋转角应尽可能小。从球面格网角度来看,应采用等积格网对其进行划分,从划分好的各个小区域几何中心位置观察卫星并进行成像,即能得到绕双轴旋转的不同视角下的二维图像。当从不同的格网中心观测时,相当于卫星目标的俯仰角、方位角在发生变化。目前较成熟的球面等积格网划分方法是基于施耐德投影的格网生成算法,通过施耐德等积多面体投影正变换建立球面和多面体表面的对应关系,从而将问题转化到平面。只需要在多面体表面构建平面网格,再通过投影逆变换映射到球面即可。根据文献[6]中的方法,选择六边形对二十面体进行剖分,其具体步骤如图 2所示[7]。
|
| 图 2 球面等积网格构建 Fig. 2 Construction of Spherical Equal-Area Grid |
利用六边形对二十面体进行分割时,第 n层上的六边形单元数为10×3n-1+2,n=1,2,…k,前五层单元数分别为12、32、92、272和812。因此,可根据姿态估计的精度要求选择创建不同分辨率的网格,对应生成不同大小的姿态数据库。若选择利用第四层次的网格划分,则可以获得卫星在不同视角下的272个模拟姿态数据。此时,若观察球半径为r,则单个六边形格网边长a=0.133 4r。以各个格网中心点为观察点,则相邻观察点之间夹角θ=7.632°,这也是数据库相邻姿态间的角度偏差。
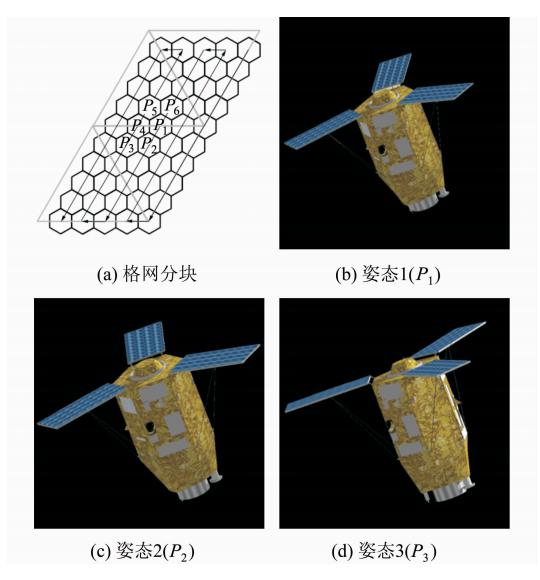
模型姿态只需与特征检索对应,不必考虑对应格网编码或观察点空间坐标,因而只要求实现遍历剖分格网的同时获得各个视图即可。为简化视点遍历过程,对等积格网分块时可以将图 2(b)的20个三角形合并为5个四边形,并依次编号,分块后的视点在格网区域内的移动方向如图 3(a)所示。
|
| 图 3 视点变化与二维视图生成 Fig. 3 Change of Viewpoint and Generation of 2D View |
由于视点的位置变化相当于卫星沿相反方向的旋转,因此,将旋转角度为固定值θ,旋转方向与视点移动方向相反,在每次旋转后获取目标二维视图,依此生成姿态数据库。本文采用六个相邻视点位置(P1,P2,…,P6)的卫星姿态数据进行实验,图 3(b)、3(c)、3(d)分别为前三个视点对应的卫星姿态二维视图。
2 图像预处理与部件分割 2.1 成像仿真
为验证姿态估计的精度,本文采用模拟光学望远镜采集的CCD图像进行实验:利用卫星的三维模型,综合考虑大气湍流和噪声污染的影响,生成空间目标观测图像。采用姿态1对应的视图作为观测图像,如图 4(a)所示。所采用的成像退化模型为长曝光大气湍流模型[8],光学系统长曝光光学传递函数(optical transfer function,OTF)定义为:
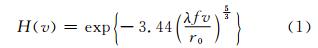

|
| 图 4 模拟观测图像生成 Fig. 4 Observed Image Simulation |
式中,λ表示波长;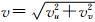 为频率;f为望远镜焦距;r0为大气相干长度。本文的大气相干长度选择为5 cm。另外,添加泊松噪声及方差为0.001的高斯白噪声,最终生成的模拟退化图像如图 4(b)所示。
为频率;f为望远镜焦距;r0为大气相干长度。本文的大气相干长度选择为5 cm。另外,添加泊松噪声及方差为0.001的高斯白噪声,最终生成的模拟退化图像如图 4(b)所示。
2.2 图像预处理
图像预处理的主要工作是消除原始图像中噪声与湍流的影响,提高图像清晰度,便于目标的识别与分割,这需要利用图像复原的方法进行处理。
对于大多数光学成像系统,可近似认为退化过程是线性不变的,其成像过程可表示为:
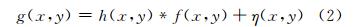
其中,*表示卷积,h(x,y)是系统的点扩散函数(point spread function,PSF),用来表示图像获取中所有的退化过程,它与加性噪声η一起作用于输入图像f(x,y),并产生退化图像g(x,y)。
若PSF和噪声类型已知,则可利用逆滤波或维纳滤波等方法进行解卷积,从而复原出原始图像。但在天文观测中,大气湍流的强度和分布都具有很大的随机性,有关成像系统PSF的信息是部分已知或完全未知的。这种情况下,就需要利用盲解卷积的方法,直接根据降质图像复原出理想结果。
针对受混合噪声影响的天文观测图像,本文采用一种改进的最大似然盲解卷积算法进行处理[9],该算法是一种迭代型的盲解卷积算法,在图像复原领域应用广泛。基于混合噪声模型的最大似然算法综合考虑了高斯噪声和泊松噪声的影响,且算法稳定性和准确性均较好。已知第k次结果fk时,其新的迭代结果为:
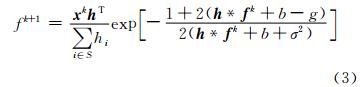
其中,高斯噪声的方差σ2以及泊松噪声的均值b的近似值可以利用矩估计法得到。由于图像分割需要去除卫星表面纹理,因此,将平滑过程加入图像复原中,在每次迭代之后利用小卷积模板对迭代结果进行一次滤波,使最终结果更有利于分割处理。
2.3 图像分割
图像分割的目的有两个:①将卫星整体从背景中提取出来;②将卫星主体与各块帆板分离,以便于分别提取各个子部件的几何特征。针对这两个目的需要采用不同的分割方法。
对于空间目标图像而言,在去除湍流及噪声影响之后,背景较为单一,因而很容易利用阈值化分割方法将目标整体与背景分割开来。利用迭代式阈值选择法,采用图像灰度中值作为初始阈值进行分割,可以较精确地将卫星整体从背景中提取出来。
考虑到主体部分灰度变化的连续性,采用区域生长法进行处理。区域生长是基于物体有平滑均匀的表面,与图像中灰度恒定或缓慢变化的区域相对应。边缘所包围的部分可以看作是区域,通过寻找阈值,使得分割后同一区域中的各像素灰度分布具有同一统计特性。采用区域生长法可将卫星主体与帆板近似分割开来。但由于卫星边缘处的灰度近似性和连续性,分割结果并不十分理想。图 5给出了图像复原以及二次分割后得到的结果。

|
| 图 5 图像复原与分割结果 Fig. 5 Results of Image Restoration and Segment |
为了得到完整的卫星主体,并消除中间的孔洞,扩展并平滑边缘,可以对区域生长法分割得到的二值图像进行先膨胀后腐蚀的闭运算,通过实验分别确定膨胀和腐蚀的次数以达到理想效果。然后将分割出的目标图像与结果图像相减,则可得到彼此分离的卫星帆板。为了补偿在图像恢复及前两次分割过程中损失的目标边缘信息,采用不对称的开运算,在不影响目标特征的情况下,适当增加膨胀次数以得到更准确的结果。图 6分别给出了形态学处理前后的子部件二值图像。

|
| 图 6 形态学处理后的分割结果 Fig. 6 Segment Results after Morphology Process |
基于特征的模型匹配是目前对三维目标进行识别所使用的常用方法,模型数据库里的每条记录都对应着卫星一个姿态,匹配得到的最佳结果就可以作为卫星的初始姿态。但基于灰度特征的匹配受限于成像质量等因素,而且往往十分耗时,运算效率很低。
为避免这一问题,可采用检索技术对不同姿态进行编码[10]。其基本思想是使数据库里的每个姿态对应一个唯一的检索值,比较观测图像提取的特征检索与数据库里的各个模型的检索值,通过计算最小欧氏距离确定最佳匹配。由于模型数据库里的各个模型分别对应于卫星的某个姿态,为了将这一检索方法应用到姿态估计问题中,需要找到一些与视角相关的特征。这样的特征在给定视角下对模型的描述是唯一的。最明显的特征是子部件的数目,其他一些特征,如子部件的面积及各部件之间的距离等也是很好的与视角相关的变量。
根据以上分析,定义一个N×N的矩阵M,N为模型中子部件的数目。(i,j)处的值Mii为第i个部件的表面积ai与最大子部件面积amax之比。(i,j)处的值Mij为1- dij/dmax 2,其中,dij为第i个部件与第j个部件质心距离之比,dmax为所有部件质心间的最远距离。因此,当两个部件彼此间隔很远时,Mij趋近于1,反之,Mij趋近于0。这样,矩阵的非对角线元素就表达了模型中各部件的邻接性。矩阵M即可用来作为某一模型的检索值,利用该矩阵的特征向量对模型进行编码,其优势在于模型的部件数目与矩形的非零特征值数量相同,而且得到的特征值是尺度不变、二维旋转不变以及平移不变的。
特征检索的过程可分为两步:首先计算图像模型化后的检索值,然后计算该值与数据库中的检索值间之的欧氏距离,具有最小距离的姿态模型被认为是目标的估计姿态。若进行比较的两个检索具有不同维数,可以将较小维数的检索扩充并补零。一般而言,这种情况是由于若干子部件被遮挡导致的,因此可以看作是高维数的检索值在某方向的映射。
3.2 几何特征提取
为了进行目标图像及姿态模型的特征检索,需要得到卫星子部件的质心、面积等几何特征。这些几何特征可以通过将分割后的各子部件分别拟合为基本几何体来得到,关键是使拟合形状的质心、面积、长轴与短轴等几何特征尽可能接近真实部件。
对卫星子部件进行拟合的过程同时也是一个对边界或区域进行表示和描述的过程。为了将分割后得到的子部件拟合为基本几何形状,本文考虑利用一些简单的区域描绘子来进行表达。常用的区域描述子包括区域面积、质心、拓扑特性、纹理和不变矩等。区域面积描述了区域的大小,计算区域面积的一种直接方法就是对该区域的像素进行计数,而区域质心的坐标可通过计算其一阶矩得到。
大小为M×N的数字图像f(x,y)的二维(p+q)阶矩定义为:
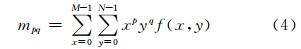
其中,p=0,1,2,…,q=0,1,2,…。相应的(p+q)阶中心矩定义为:
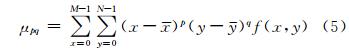
图像的两个一阶矩m10和m01用来确定区域的质心。其质心坐标为:
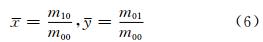
区域对象的延伸方向(即长轴方向)可定义为:
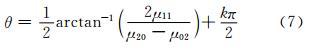
其几何意义是与区域有相同二阶矩的椭圆长轴与x轴夹角。区域的长轴a与短轴b也同样用此椭圆的长轴与短轴长度近似:
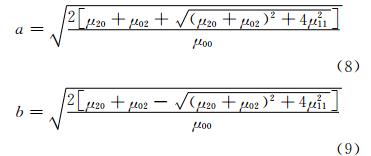
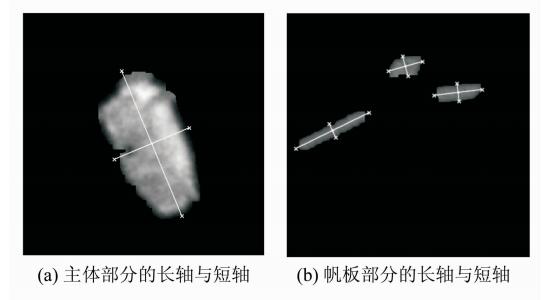
通过计算区域的一阶矩和二阶矩,可以分别获得区域的质心和长短轴,结果如图 7所示。
|
| 图 7 卫星部件的几何特征 Fig. 7 Geometric Features of Satellite Components |
通过计算,我们可以分别得到各部件的长短轴长及区域面积(像素数)。另外,拟合椭圆和拟合矩形的面积分别由长短轴长度按相关面积公式计算得到,结果如表 1所示(图 7(b)由左至右三块区域分别对应帆板1~3)。
| 主体 | 帆板1 | 帆板2 | 帆板3 | ||
| 质心 | X | 137.3 | 48.6 | 125.4 | 180.9 |
| Y | 138.3 | 123.6 | 56.2 | 83.6 | |
| 长度 | 长轴 | 165.7 | 85.9 | 37.4 | 50.9 |
| 短轴 | 86.0 | 15.9 | 21.5 | 19.0 | |
| 面积 | 区域 | 10 985 | 989 | 585 | 717 |
| 椭圆 | 11 194.2 | 1 075.0 | 631.0 | 760.1 | |
| 矩形 | 14 253.0 | 1 368.7 | 803.4 | 968.6 | |
通过比较三种计算方法得到的部件面积可以看出,外接椭圆与外接矩形面积均大于区域所占的像素数,由于分割过程中边缘像素值的损失以及某些姿态的遮挡影响,区域的像素数往往比实际面积要小;而与矩形面积相比,椭圆面积与真实面积相差不大,更接近实际情况。综合考虑这两方面因素,选择拟合椭圆的面积进行计算。
获得子部件几何参数后,由质心坐标计算各部件间的欧氏距离,结果如表 2所示。
| 主体 | 帆板1 | 帆板2 | 帆板3 | |
| 主体 | 0 | 89.9 | 83.0 | 70.0 |
| 帆板1 | 89.9 | 0 | 102.2 | 138.2 |
| 帆板2 | 83.0 | 102.2 | 0 | 61.9 |
| 帆板3 | 70.0 | 138.2 | 61.9 | 0 |
根据表 1和表 2计算得到的结果,分别计算 1-(dij/dmax)2与ai/amax,可以得到该观测图像的特征检索矩阵 M :
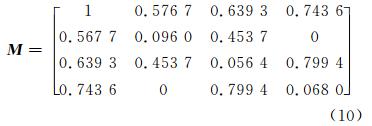
该矩阵的特征向量为[-0.886 7 -0.129 1 0.120 1 2.116 1],这便是由观测图像最终得到的特征检索向量。
3.3 姿态模型匹配
利用特征检索方法得到姿态模型各部件质心与面积等信息后,就可以分别生成各个模型对应的特征向量,计算待估计目标的检索向量与它们之间的欧氏距离,距离最小的模型姿态就可以作为目标的概略姿态。
由于姿态数据库的视图为理想清晰图像,因而生成模型检索向量的过程更为简单,将图像复原过程改为低通滤波,以平滑目标表面纹理,使各个部件内的灰度分布趋于统一。在此基础上进行图像分割与形态学处理,提取几何特征并获取各个姿态对应的特征向量。
为验证检索向量匹配的精度,分别利用本文方法获取P1~P6六个姿态模型的特征检索向量,并求其与观测图像检索向量的欧氏距离,结果如表 3所示。
| 姿态 | 检索向量 | 欧氏距离 |
| 姿态1 | [-0.820 3 -0.011 6 0.192 3 2.093 7] | 0.143 4 |
| 姿态2 | [-0.911 8 -0.060 2 0.231 2 2.014 5] | 0.164 0 |
| 姿态3 | [-0.753 1 -0.013 4 0.209 2 2.092 1] | 0.186 7 |
| 姿态4 | [-0.616 8 -0.137 8 0.248 0 2.170 4] | 0.290 5 |
| 姿态5 | [-0.841 5 -0.027 7 0.301 4 1.941 0] | 0.269 4 |
| 姿态6 | [-0.522 5 -0.172 6 0.383 0 2.145 4] | 0.439 1 |
其中,姿态1对应的图像为本文模拟实验所用的原始图像。结果表明,观测图像的最佳匹配为姿态1,它们特征检索之间的欧氏距离最小,姿态2和姿态3与之相差不大,这也与二维视图情况相符。实验结果表明,该方法可以在接近真实天文观测的情况下,成功进行匹配并准确得到卫星的三维姿态估计,估计精度至少为7.632°。
4 结 语
本文提出并实现了一种利用天文观测图像估计空间目标三维姿态的方法。对于简单卫星模型而言,各子部件形状较为规则,可直接将其拟合为矩形或椭圆。对于复杂空间目标,需要利用不规则多边形进行拟合,再提取多边形的几何特征。另外,本文姿态估计方法是将目标姿态与模型数据库里某条记录对应起来,其实际姿态可能不在数据库中。因而在以后的研究中,可以将该估计结果作为目标的粗略姿态,采用二维仿射变换等方法进行进一步优化。
| [1] | Weeden B C, Cefola P J. Computer Systems and Algorithms for Space Situational Awareness: History and Future Development[C]. The 12th International Space Conference of Pacific-basin Societies, Quebec, Canada, 2010 |
| [2] | Yang Yubin, Lin Hui. Automatic Detecting and Tracking Space Debris Objects Using Active Contours from Astronomical Images[J]. Geomatics and Information Science of Wuhan University,, 2010, 35(2): 209-214 (杨育彬,林珲. 利用天文观测图像对空间碎片目标进行自动识别与追踪[J]. 武汉大学学报·信息科学版,2010,35(2): 209-214) |
| [3] | Gao Xin, Wang Jianli, Zhou Sizhong. Photometric Characteristic Measurement of Space Target [J]. Opto- Electronic Engineering, 2007, 34(3): 42-45 (高昕,王建立,周泗忠. 空间目标光度特性测量方法研究[J]. 光电工程, 2007, 34(3): 42-45) |
| [4] | Shi Min, Zhang Shusheng, Li Liang, et al. 3D CAD Model Retrieval Using 2D Characteristic Views[J]. Manufacturing Automation, 2012,34(5):82-84 (石民,张树生,李亮,等. 基于二维典型视图的三维CAD模型检索算法[J]. 制造业自动化,2012,34(5):82-84) |
| [5] | Fan Jia, Li Yingchun, Sun Huayan. The Algorithmic Research of Space Object Identification from Multi-viewpoints[J]. Journal of the Academy of Equipment Command & Technology, 2009,20(6):55-59 (樊佳,李迎春,孙华燕. 多视点空间目标识别方法研究[J].装备指挥技术学院学报,2009,20(6):55-59) |
| [6] | Sahr K, White D, Kimerling A J. Geodesic Discrete Global Grid Systems[J]. Cartography and Geographic Information Science, 2003, 30(2): 121-134 |
| [7] | Zhang Yongsheng, Ben Jin, Tong Xiaochong. The Earth Spatial Information Spherical Discrete Grid[M]. Beijing: Science Press, 2007(张永生,贲进,童晓冲.地球空间信息球面离散网格[M].北京:科学出版社,2007) |
| [8] | Geng Zexun, Chen Bo, Wang Zhenguo, et al. The Theory and Method of Adaptive Optics Image Restoration[M]. Beijing: Science Press, 2010 (耿则勋,陈波,王振国,等. 自适应光学图像复原理论与方法[M]. 北京:科学出版社,2010) |
| [9] | Benvenuto F, Camera A L, Theys C, et al. The Study of an Iterative Method for the Reconstruction of Images Corrupted by Poisson and Gaussian Noise[J]. Inverse Problems, 2008, 24(3): 1-20 |
| [10] | Wang Yinghong. Image Indexing and Similarity Retrieval Based on Spatial Relationship Model[J]. Information Sciences, 2003, 154: 39-58 |
 2015, Vol. 40
2015, Vol. 40


