文章信息
- 王立, 吴雄斌, 马克涛, 沈志奔
- WANG Li, WU Xiongbin, MA Ketao, SHEN Zhiben
- 利用X波段导航雷达探测海洋表面流速的方法
- A Method to Detect Ocean Surface Current Based on X-Band Marine Radar
- 武汉大学学报·信息科学版, 2015, 40(1): 90-95
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 90-95
- http://dx.doi.org/10.13203/j.whugis20130295
-
文章历史
- 收稿日期:2014-07-04
海流又称洋流,是海水因热辐射、蒸发、降水、冷缩等而形成密度不同的水团,再加上风应力、地转偏向力、引潮力等作用而大规模相对稳定的流动,它是海水的普遍运动形式之一。海流的运动与海上安全、海洋工程、海洋战争等都密切相关。传统的海表面流测量方法有现场观测、立体摄影以及雷达探测。现场观测在一定的时间内得到一片小区域的数据,无法全面反映所测海域的真实海况,并且现场设备很难维护。同时,立体摄影获取海流信息的方法受限于仪器的载体并且受到环境的限制,黑夜或者有雾、有云的情况下,这种方法无法实施,而且立体摄影的后续处理手续十分复杂。利用雷达观测海洋信息能克服以上方法的不足,它的全天候、高分辨率等优势使得利用雷达来获取海流信息越来越成为了当今世界的主流,由武汉大学研制的OSMAR系列高频地波雷达已在我国沿海开展业务化运行,并且取得了很好的效果。作为雷达探测海洋手段的补充,X波段导航雷达测波系统的发展使得雷达探测手段更为多样、精确。
X波段导航雷达广泛用于海上交通管理和海上航行导航,近三十年来逐步发展成为一种用于海洋环境监测的新手段。当X波段测波雷达电磁波入射到海面时,与那些与雷达波长相当的、由风引起的毛细波产生Bragg散射,后向散射回波被雷达接收器接收,形成“海杂波”[1, 2],而波长较长的重力波通过对毛细波的流体动力调制、倾斜调制、阴影调制作用表现在海杂波图像上[3]。因此,X波段导航雷达回波图像包含着丰富的海洋动力学参数信息。对雷达回波图像进行分析可以找到与海洋表面动力学过程(风、浪、流)相对应的谱特征,由此即可提取和反演出海面动力学要素值。利用X波段导航雷达进行海洋监测具有便捷、可靠、经济、实时和分辨率高等特点,已经引起了海洋学家们的广泛重视,被认为是一种能对海洋进行有效监测的高科技手段。
目前,国际上已经有两家公司对X波段雷达的浪流观测进行了系统的开发,一个是德国 GKSS 研究中心,另一个是挪威 Miros 公司。从20世纪 80 年代开始,德国 GKSS 实验室一直致力于研究基于 X 波段雷达的波流监测系统,经过十几年的实验开发,直到 1995 年,研制成功了商业化的波流监测系统 (wave monitoring system,WaMoS)。今天,该系统在许多方面作了改进,形成了第二代产品 WaMoS II。WaMoS II 通过分析 X 波段雷达的海杂波序列图像,能够给出海浪谱、海浪参数和表层流参数。挪威 Miros 公司也研制了类似的波流监测系统 WAVEX,并在 1996 年开发形成商业化产品。WAVEX 也具有和 WaMoS II 相同的功能,进而获得波、流参数。除此之外,美国、日本、丹麦、荷兰、意大利等国也在从事利用 X 波段雷达进行海洋监测的研究。我国在利用 X 波段雷达进行海洋监测方面的研究起步相对较晚。“十五”期间,总装备部和国家863计划海洋技术主题突破了 X 波段雷达的海浪场和海面流场提取关键技术,但目前还没有达到商业化的程度。近几年,国内几个科研院校加大了自主研发的速度,在理论和实践方面开展了一些工作,如国家海洋技术中心、中国海洋大学、大连海事大学、哈尔滨工程大学、武汉大学和中国科学院海洋研究所等[4]。
在海浪参数反演过程中,首先对X波段雷达接收的回波图像序列进行三维快速傅里叶变换(FFT),以获得相对海浪方向谱,然后利用海浪方向谱可以计算得到海浪的主波周期和主波向等信息。由于海流的存在,使得朝向雷达天线方向的回波图像功率谱由于多谱勒效应而移到高频部分,反之则移至低频部分。因此,流速的确定是准确计算图像功率谱的关键,对于利用回波图像功率谱反演准确的海浪参数信息是至关重要的[5]。传统的基于X波段导航雷达的海流反演算法是基于加权最小二乘法,经过三维FFT变换的谱的所有频点都会参与运算,由于存在干扰就会使海流结果不准确,从而导致反演得到的海浪参数不准确。为了得到准确的海流信息,需要对雷达数据进行预处理,选取相对准确的满足色散关系的频点。目前对雷达数据的预处理都是用已知的最大海流流速进行带通滤波[6],然而对观测海域海流最大可能流速未知,或对于船载X波段测波雷达来说,用流速来对回波谱进行限制就会失效。针对目前预处理算法的不便,本文进行了新的预滤波研究。
1 测流算法研究 1.1 几何模型预滤波
基于X波段测波雷达的海洋回波图像在进行三维FFT后可以得到 kx-ky-ω空间波数频率三维谱,对于每个方向来说可以从三维谱里面提取得到k-ω的二维谱。理论上来说,对于每个方向上的k-ω谱都可以找到一条满足海洋学深水重力波色散关系[7]的曲线。对于色散关系上的每一个点来说会满足:
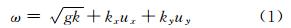
式中,ω为海浪的角频率;g为重力加速度;k为空间波数;kx为空间波数在X轴方向的投影;ux为海流在X 轴方向的投影;ky为空间波数在Y轴方向的投影;uy为海流在Y 轴方向的投影;
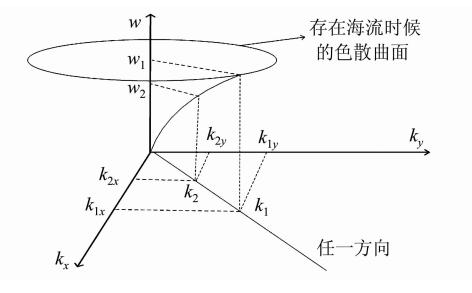
不考虑水深的影响,图 1给出了某一方向上空间波数与角频率的几何关系,对于色散关系曲线上任意两点可以得到:
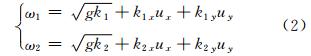
|
| 图 1 空间波数与角频率的几何关系图 Fig. 1 Geometric Relationship Between Spatial Wave Number and Radian Frequency in Random Directions |
式中,ω1、ω2为满足色散曲线上任意二点对应的角频率;k1、k2为满足色散曲线上任意二点对应的空间波数;g为重力加速度;k1x、k2x、k1y、k2y分别为k1、k2在X轴和Y轴的投影;ux、uy分别为海流在X轴和Y轴方向的投影。
由色散关系及相关几何关系(图 1)可以得到:
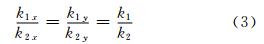
令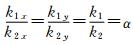 ,则
,则
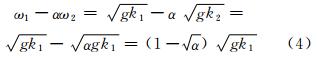
式(4)进一步变换可得:
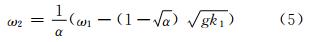
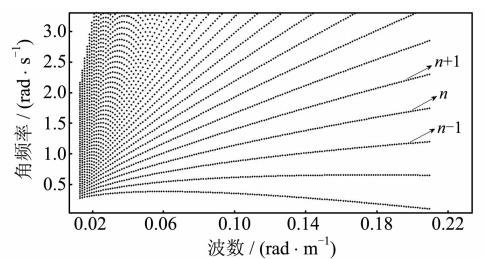
根据式(5)以及几何模型可知,每个方向上对应着一系列α值,并且是固定的一些值,对这些值都进行上述处理。对于每个方向上的k-ω面,可以生成一系列满足式(5)的曲线簇(见图 2),对于每一条曲线,利用邻近点插值法插值得到该曲线上每一点处三维FFT变换后的能量值。
|
| 图 2 由关系式来确定一系列满足关系式的曲线簇 Fig. 2 In a Certain Direction,a Series of Curves Satisfying the Relationship are Determined by the Relationship |
总的来说,满足上述色散关系曲线分布的回波点的能量比偏离了此色散关系的回波点的能量要大,因此,通过比较每个方向k-ω面上相邻曲线上通过的回波点的能量值大小,就可以在该方向上找出满足色散关系的曲线。对所有的方向重复以上处理过程,即可以得到每个方向上的色散关系曲线。
1.2 利用滤波得到的色散关系曲线反演流速
利用得到的每个方向上的色散关系曲线以及曲线上每个点对应的能量大小,运用加权最小二乘法[8],根据极小值原理,取加权最合适方差为:
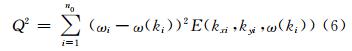
其中,ωi为对应的第i个频率的海浪的理论频率;ω(ki)为与计算出的曲线上每个点的波数ki对应的频率;E(kxi,kyi,ω(ki))代表着与计算出的波数ki对应的点的功率值,E(kx,ky,ω)=|I(kx,ky,ω)|2;n0为计算出的曲线上满足要求的点数。
为找出最佳的ux、uy值,必须先找出差值平方和的极小值,分别对ux、uy求Q2的偏微分,并使结果等于零,即可以得到流速公式为:
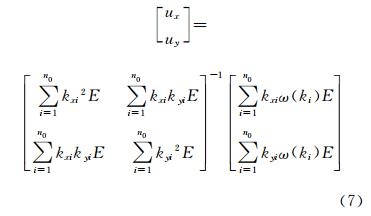
式中,ux、uy分别为流速的两分量;E即为E(kxi,kyi,ω(ki)),其他变量定义同前。
2 实验与分析2012年下半年武汉大学海态实验室在福建东南沿海进行了为期两个月的X波段导航雷达与高频地波雷达的比测分析。X波段导航雷达为武汉大学电子信息学院研制的HopeX机动式X波段测波雷达,HopeX实验站点分布如图 3所示。HopeX测波雷达实验地点位于福建龙海地波雷达站北边300 m处,两部雷达在3 km距离内的探测范围基本重合,为验证HopeX探测能力提供了较为理想的条件。本次实验通过海洋重力波色散关系及相应的几何关系式,结合最小二乘法,提出了一种新的X波段导航雷达海流反演方法,并与附近高频地波雷达海流数据的进行对比。

|
| 图 3 HopeX实验站点分布图 Fig. 3 Testing Site of HopeX X-Band Wave Monitoring Radar |
由于高频地波雷达可以输出所观测海域的海流结果,而且,龙海高频地波雷达的地点也基本上和本文的实验地点在同一地方,因此,利用龙海地波雷达的海流结果可以进行海流的对比分析。X波段利用雷达接收反射回来的“海杂波”,然后通过色散关系方程将实测图像谱联系起来,使用图像谱加权拟合出表面流。其中,这个方法的思路是使实测图像谱与理论谱的频率方差最小并且使尽可能多的谱能量大的点落在色散关系曲线上。而对于高频地波雷达来说,其利用回波信号傅里叶变换后的布拉格谱图的布拉格峰来提取出流速,然后利用双雷达站的数据合成可以得到精确的流向。本文取出高频地波雷达在实验期间的径向流数据以及流向,然后用新的方法对高频地波雷达的径向流进行了矢量合成,并且实现了定点的数据提取,在所需要得到海流数据的地方(也就是X波段雷达所探测的区域)提取出矢量流速。
表 1是2012-10-26~2012-10-28新算法与传统反演算法所得流场与高频地波雷达数据的对比结果。高频地波雷达第零个距离元的海浪回波代表着雷达站点附近海域信息,第一个距离元的海浪回波代表着距离雷达站点5 km处海域的信息。由于X波段雷达最远探测距离为5 km,因此本文只考虑高频地波雷达的第零个以及第一个距离元的海浪回波来进行对比验证。值得指出的是,高频地波雷达的第零个距离元和第一个距离元所得到的海浪数据是不太稳定的。此区域内获得的浪场信息与风场信息不确定性较大,但是流场数据相比较而言精确性与稳定性都要远远高出浪场信息与风场信息。而且本文利用X波段雷达观测区域(距离站点3 km左右海域)附近大量的高频地波雷达第零个距离元与第一个距离元的数据来矢量合成最终的结果,即可以使两雷达海流结果在3 km探测区域重合(利用最小二乘法),并且确保了同区域用来对比的高频地波雷达流场数据的有效性与精确性。
| 日期 | 流速误差/(cm·5s-1) | 流速相关系数 | 流向误差/(°) | 流向相关系数 | 样本点数/个 | ||||
| 新算法 | 传统算法 | 新算法 | 传统算法 | 新算法 | 传统算法 | 新算法 | 传统算法 | ||
| 2012-10-26 | 9.1 | 15.1 | 0.77 | 0.59 | 33.2 | 45.4 | 0.75 | 0.55 | 54 |
| 2012-10-27 | 11.1 | 13.6 | 0.73 | 0.60 | 29.1 | 38.6 | 0.78 | 0.67 | 77 |
| 2012-10-28 | 9.9 | 13.9 | 0.60 | 0.51 | 25.2 | 31.0 | 0.60 | 0.52 | 86 |
| 2012-10-29 | 12.1 | 12.9 | 0.64 | 0.62 | 39.8 | 43.5 | 0.79 | 0.66 | 51 |
| 全部数据 | 10.8 | 13.7 | 0.62 | 0.57 | 32.7 | 40.1 | 0.76 | 0.63 | 268 |
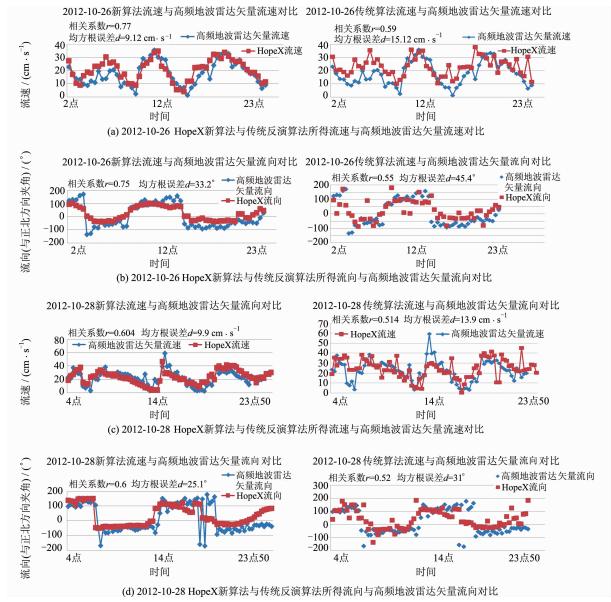
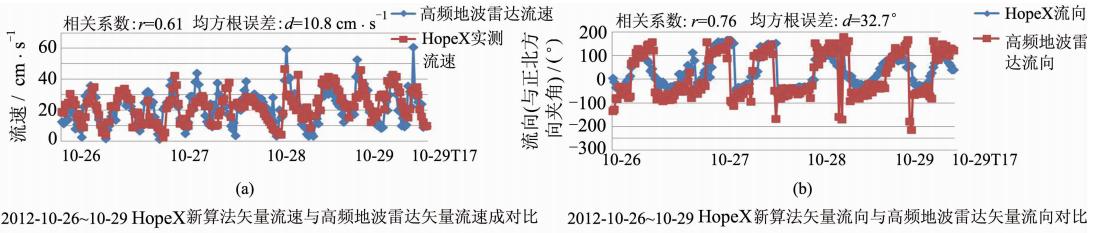
地波雷达距离分辨率是5 km,而X波段雷达参与反演的距离仅为3 km左右,并且分辨力可以达到10 m左右。图 4显示了部分日期(10月26和28日)HopeX新算法与传统反演算法所得海流与地波雷达海流的对比,图 5是HopeX新算法所得海流与高频地波雷达海流数据的综合对比。
|
| 图 4 10月26和28日HopeX新算法与传统反演算法所得海流与地波雷达海流对比 Fig. 4 Comparison of the Ocean Surface Current Measured by the HopeX with that Retrieved from Nearby HFGWR during the Period of October 26 and October 28 in 2012 |
|
| 图 5 HopeX新算法海流与高频地波雷达海流数据综合对比 Fig. 5 Comprehensive Comparison of the Ocean Surface Current Measured by the New Algorithm with that Retrieved from Nearby HFGWR |
由图 4、表 1可知,本文新算法在流速、流向反演方面有三个方面改善:① 新算法流速、流向与高频地波雷达流速、流向具有很好的一致性。与传统算法相比较而言,本文算法所得流速、流向与参考值的相关系数有较大提高。② 本文算法所得流速、流向较传统算法精确度更高。与传统算法相比较而言,本文算法所得流速、流向与参考值的误差有很大改善。③ 本文算法所得流速、流向奇异值大量减少,数据趋势更为合理。图 5的总体分析表明,HopeX新算法流速与地波雷达流速的标准误差分布在(9.1~12.1 cm/s)的范围中,本文算法全部数据综合对比的标准误差为10.8 cm/s,而传统算法所得数据的标准误差为13.7 cm/s。本文算法全部数据综合对比的相关系数为0.62,而传统算法所得数据的相关系数为0.57;流向的标准误差分布在(29.1°~39.8°)的范围中,本文算法流向的标准误差为32.7°,而原始算法为40.1°;本文算法流向的相关系数为0.76,而原始算法为0.63。总体来讲,本文算法所得海流结果与传统反演算法所得海流结果相比较,精度与稳定性都有较大提高。
3 结 语
X波段导航雷达具有便捷、可靠、经济、实时和分辨率高等特点,可以用来进行海洋流速的监测。本文针对X波段导航雷达,提出了一种探测海洋表面流的方法,此方法结合几何滤波模型来对回波数据进行滤波,使反演流速结果更为准确。与高频地波雷达同区域流速的对比分析表明本文方法是可行、有效的。与传统X波段导航雷达测流方法相比,此方法不需要预先知道探测海域的最大流速信息,为相对流速较高场合海域探测以及船载X波段导航雷达测流技术的发展提供了有力的技术支持。
| [1] | Young I R, Rosenthal W, Zimmer F. A Three Dimensional Analysis of Marine Radar Images for Determination of Ocean Wave Directionality and Surface Currents[J]. Journal of Geophysical Research, 1985, 90(C1):1 049-1 059 |
| [2] | Tian Jiansheng, Wu Shicai, Yang Zijie, et al. Noise Researched in HFGW Radar Sea Echo Processing[J]. Chinese Journal of Radio Science, 2002,17(4):396-400(田建生,吴世才,杨子杰.高频地波雷达海洋回波处理中的噪声研究[J].电波科学学报,2002,17(4):396-400) |
| [3] | Senet C M, Seemann J, Flampouris S. Determination of Bathymetric and Current Maps by the Method DISC Based on the Analysis of Nautical X-Band Radar Image Sequences of the Sea Surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(8):2 267-2 279 |
| [4] | Cui Limin. Study on Remote Sensing Mechanism and Retrial Method of Ocean Wave and Current with X Band Radar[D]. Qingdao: Marine Research Institute of Chinese Academy of Sciences,2008(崔利民. X波段雷达海浪与海流遥感机理及信息提取方法研究[D]. 青岛:中国科学院海洋研究所,2008) |
| [5] | Wu Y Q, Wu X B, Chen F, et al. Basic Analysis on the Extraction of Ocean Dynamic Parameters with an X-band Radar[J]. Journal of Remote Sensing, 2007,11(6): 817-825 |
| [6] | Rune G. Ocean Current Estimated from X-Band Radar Sea Surface Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(4):783-792 |
| [7] | Wen S C, Yu Z W. Wave Theory and Principle of Calculations[M]. Beijing: Science Press, 1984(文圣常,宇宙文. 海浪理论及计算原理[M]. 北京:科学出版社,1984) |
| [8] | Seemann J, Senet C M, Dankert H, et al. Radar Image Sequence Analysis of Inhomogeneous Water Surfaces[C]. SPIE Conf. on Applications of Digital Image Processing XXII, Washington D C, 1999 |
 2015, Vol. 40
2015, Vol. 40



