文章信息
- 耿迅, 徐青, 邢帅, 侯一凡, 蓝朝桢
- GENG Xun, XU Qing, XING Shuai, HOU Yifan, LAN Chaozhen
- 火星快车HRSC线阵影像投影轨迹法近似核线重采样
- Approximate Epipolar Resampling of Mars Express HRSC Linear Pushbroom Imagery Based on Projection Trajectory Method
- 武汉大学学报·信息科学版, 2015, 40(1): 40-45
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 40-45
- http://dx.doi.org/10.13203/j.whugis20130192
-
文章历史
- 收稿日期:2013-05-30
2. 61363部队, 陕西 西安, 710054;
3. 地理信息工程国家重点实验室, 陕西 西安, 710054
2. Unit 61363, Xi'an 710054, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China
火星是太阳系内最有可能发现生命痕迹的行星,科学家甚至梦想人类有一天能够移居火星。通过火星全球勘测者(MGS)、火星快车(MEX)、火星侦察轨道器(MRO)等轨道探测器以及勇气号、机遇号、凤凰号、好奇号等火星着陆探测器任务的成功执行,人类对火星已经有了全新的认识。火星地形测绘是开展火星研究的基础,获取高分辨率火星地形数据也是着陆器安全着陆的前提。利用摄影测量方法对火星表面立体影像数据进行处理仍然是当前获取火星地形数据的主要方法[1, 2, 3]。欧洲空间局2003年发射的火星快车探测器搭载了专门用于火星地形测绘的高分辨率立体相机(high resolution stereo camera,HRSC)线阵相机,通过对HRSC影像进行摄影测量处理可以获取火星全球高分辨率地形数据[4, 5, 6]。HRSC影像摄影测量数据处理的核心问题之一是线阵影像的高精度、快速、密集匹配,利用核线几何约束是解决这一问题的有效方法。
由于线阵相机行中心投影的特殊性,线阵影像的核线几何关系比框幅式影像复杂。文献[7]基于共线方程严密几何模型推导了线阵影像核线方程,但是该公式形式复杂,且为非线性形式,难以实际应用。文献[8]研究了速度与姿态为常量时的卫星线阵影像核线几何关系。文献[9]利用平行投影模型对卫星影像核线重采样方法进行了研究。文献[10]利用拟合法研究了SPOT系列影像的近似核线排。文献[11]研究了基于有理函数模型的线阵CCD影像水平纠正方法。文献[12, 13]采用线性模型简化了同名核曲线,提出了一种实用的卫星影像近似核线重采样快速算法,并提出了基于物方投影基准面生成近似核线影像的方法。文献[14]提出了一种基于有理多项式系数与物方经纬度的线阵卫星影像近似核线重采样方法。在分析线阵影像核线几何关系时,通常对传感器模型进行简化或进行某种近似处理,如文献[7]将位置与姿态表示为二阶多项式形式,文献[8]的核线几何分析建立在速度与姿态保持基本不变的前提下,显然,这些核线几何模型的适用性有限。可见,线阵推扫式影像的核线理论并未成熟,也未形成统一、通用的核线几何公式或者核线理论模型,因此,高精度、高效率的线阵核线影像生成方法仍然值得深入研究。
目前,可以公开获取的火星全球地形数据是由MGS任务数据处理而成的,分辨率为1/128°×1/128°,约为400~500 m,分辨率仍然比较低,而HRSC影像是获取火星全球高分辨率地形数据的理想数据源。本文首先利用投影轨迹法分析火星快车HRSC线阵影像的核线几何关系,然后基于严密几何模型将HRSC线阵影像纠正至水平影像,并分析核线在水平影像上的几何关系,在此基础上,提出了一种适用于火星快车HRSC线阵影像的近似核线重采样方法。
1 投影轨迹法核线基本原理由于线阵推扫式影像行中心投影的特殊性,它不能像框幅式影像那样建立严格的核线几何关系,通常使用投影轨迹法分析线阵影像的核线几何特性。投影轨迹法基于共线条件方程,理论最为严密,其基本原理如图 1所示。
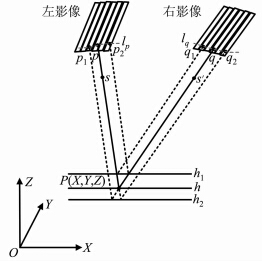
|
| 图 1 投影轨迹法线阵影像核线基本原理 Fig. 1 Basic Principle for Epipolar Line Geometry of Linear Pushbroom Imagery |
地面点 P(X,Y,Z)在左右影像上分别成像于p、q,像点p与地面点P以及该扫描行的投影中心S(Xsi,Ysi,Zsi)可构成一条投影光线,该投影光线与物方空间水平面hi相交得到一系列交点Pi,将Pi反投影至右影像上可得到一系列的点qi,这一系列的点qi构成像点p的核曲线lq。显然,p点的同名像点q一定位于核曲线lq上。同理,将右影像上的像点q、投影中心S′以及地面点P构成的投影光线与物方水平面进行相交,将交点反投影至左影像上也可得到一系列的点,构成q的核曲线lp,q的同名像点p也必然位于lp上。
由于线阵推扫式影像的行中心投影特性,外方位元素随扫描行变化,基于投影轨迹法得出的线阵影像核线方程形式复杂,且为非线性形式,不能直接用于核线重采样。根据研究人员对线阵影像核线几何的研究以及投影轨迹法的核线几何关系,可以得出如下结论[15]。
1) 线阵影像不存在类似框幅式影像严格定义的核线,线阵影像的核线也不是直线,而是类似双曲线。
2) 局部范围内线阵影像核线接近于直线。
3) 线阵影像不存在严格定义的同名核线对,但是局部范围内存在一一对应的核线,以此为依据,可以将线阵影像的匹配由二维搜索转换为一维搜索。
2 HRSC影像近似核线重采样 2.1 火星快车HRSC严格几何模型火星快车是欧洲空间局的首个火星探测任务,于2003年6月发射,2003年12月飞抵火星,目前仍在轨飞行并不断发回火星高分辨影像数据。火星快车上搭载的HRSC相机专用于火星地形测绘,获取的高分辨率影像已基本覆盖火星全球,轨道高度为250 km时,其全色波段影像分辨率可达10 m。HRSC相机可同时获取9个波段线阵影像,即5个全色波段和4个多光谱波段(红、绿、蓝与近红外),9条线阵CCD平行安置在焦平面上,每条线阵CCD有5 184个像素,坐标系 Y轴与探测器飞行方向相同,X轴沿线阵CCD排列方向并垂直于Y轴,Z轴垂直于焦平面且指向摄影方向,XYZ三轴构成右手系。
获取HRSC的初始外方位元素涉及时间及坐标系转换,即先确定火星的时空基准。本文将时间转换为J2000历书时,摄影测量物方坐标系统一转换至火星地固坐标系。火星参考椭球为正球体,半径为3 396.0 km,本初子午线定义在Airy-0陨石坑中心区域[16],经纬度定义方式与地球相同。时间、坐标系转换以及传感器几何参数利用NAIF提供的SPICE库进行[17]。
根据HRSC相机几何参数以及由SPICE库转换得到的影像外方位元素等信息可构建火星快车HRSC影像严格几何模型,公式为:
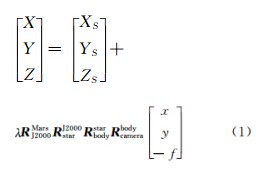
其中,(x,y)为HRSC影像上的像点坐标;(X,Y,Z)为火星地面点坐标;(XS,YS,ZS)为精密定轨后的火星探测器位置; R J2000Mars为J2000坐标系到火星地固坐标系旋转矩阵; R starJ2000为星敏感器测定的探测器姿态; R bodystar为卫星本体至星敏感器的旋转矩阵; R camerabody为相机与卫星本体间的安装矩阵。
2.2 线阵影像微分纠正生成相对水平影像框幅式影像的核线重采样可通过将原始倾斜影像纠正至水平影像的方法实现[18]。对于线阵影像核线重采样问题,可以借鉴框幅式影像微分纠正生成水平影像的方法,在水平影像上进行核线重采样。因此,本文基于投影轨迹法先分析同名像点在原始影像上的核线几何关系;然后,给定平均高程面作为投影面,对线阵影像进行微分纠正获取水平影像;由于水平影像与原始影像可以建立严格的转换关系,因此可以将原始线阵影像上的核线转换至水平影像,分析核线在水平影像上的几何关系并确定核线方向,再在水平影像上进行核线重采样。
如图 2所示,原始影像上的同名像点 p、q对应于水平影像上的同名像点p′、q′,基于投影轨迹法获取的核线lp与lq在水平影像上形成L′ p与L′ q,核线方向接近于探测器飞行方向,而探测器飞行方向与投影面X轴方向有一定夹角,计算出该夹角后即可将水平影像沿核线方向进行重采样。
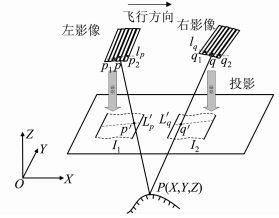
|
| 图 2 线阵CCD影像重投影生成相对水平影像 Fig. 2 Horizontal Image Generation Through Image Reprojection |
基于严密几何模型可以建立水平影像与原始影像之间的坐标转换关系,即已知原始影像上的像点坐标 (x,y)与投影面基准高程Z0,利用共线条件方程可以计算出地面点坐标(X,Y,Z),再结合水平影像上的起始点坐标(X0,Y0)与像素采样间隔d可以得出该点在水平影像上的像点坐标(xn,yn);反之,若已知水平影像上的像点坐标(xn,yn),则可计算出该点的地面点坐标(X,Y,Z),然后利用地面点反投影算法计算出原始影像像点坐标(x,y)。因此,水平影像上的像点坐标可与原始影像上的像点坐标建立起严格的对应关系。为便于描述,本文不再列出具体计算公式,而采用函数映射方式表示转换过程:
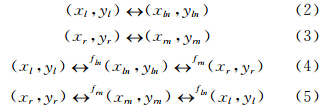
其中,式(2)表示左影像像点与水平影像上像点的相互转换,正转换表示由原始影像像点坐标(xl,yl)计算水平影像上的像点坐标(xln,yln),反变换表示由水平影像上的像点坐标(xln,yln)计算原始影像像点坐标(xl,yl)。式(3)表示右影像像点与其水平影像上像点的相互转换。式(4)、(5)表示利用地面点反投影(投影轨迹法)建立左右影像像点坐标与水平影像像点坐标的转换关系。以左影像为例,可由左影像上的像点坐标(xl,yl)计算出水平影像上的像点坐标(xln,yln),进而得出地面点坐标(X,Y,Z),进行地面点反投影获取右影像上的像点坐标(xr,yr)。上述公式是在水平影像上进行同名点量测以及立体定位的基础,即在左、右水平影像上量测出同名像点(xln,yln)与(xrn,yrn),则可将其转换为原始图像上的像点坐标,进而利用共线条件方程进行前方交会计算。
利用式(2)~(5)可以将投影轨迹法得到的核曲线上的点转换至水平影像上,由于经过微分纠正改正了影像倾斜带来的投影误差,水平影像上的核曲线L′ p与L′ q近似为一条直线,通过计算L′ p与L′ q的斜率,可以得出近似核线方向(见图 3),沿着核线方向进行重采样,即可获取近似核线影像。核线方向可通过计算核线相对于物方X 轴的夹角或者核线的斜率求出。

|
| 图 3 水平影像上核线方向与物方坐标系X轴夹角 Fig. 3 Intersection Angle Between Epipolar Line and Axis-X in Object Space |
基于上述投影轨迹法在原始图像以及水平影像上的核线几何关系分析,本文针对火星快车HRSC线阵影像提出了一种基于投影轨迹法的核线重采样方法,算法具体流程如图 4所示,核线重采样步骤如下。
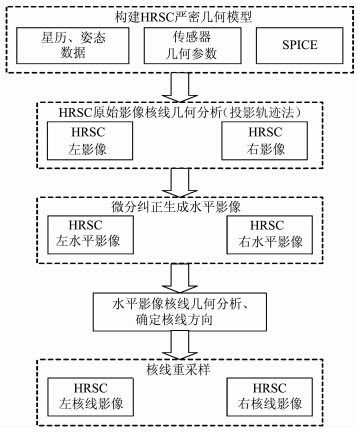
|
| 图 4 基于投影轨迹法的线阵影像核线重采样流程 Fig. 4 Epipolar Resampling of HRSC Linear Imagery Based on Projection Trajectory |
1) 构建火星快车HRSC立体影像严格几何模型;
2) 利用投影轨迹法计算像点坐标在原始图像上的核曲线;
3) 利用严格几何模型将HRSC立体影像纠正至水平影像;
4) 将原始影像上的核曲线转换至水平影像上,并计算水平影像上的核线方向;
5) 在水平影像上沿核线方向进行核线重采样。
3 实验与分析实验数据为好奇号火星探测器着陆区盖尔陨石坑附近HRSC影像,影像获取时间为2008-02-09,影像分辨率约15 m,选取HRSC 9个通道中基高比最大的S1与S2两个通道影像进行实验。
选取S1、S2影像上同名像点p(1 836.25,5 124.25)与q(1 951.50,5 430.50),利用投影轨 迹法获取p、q在对应影像上的核曲线,利用投影轨迹法分析核线时高程变化步长取为影像分辨率的三分之一,即5 m。将计算得出的核线叠加在原始HRSC图像上,核曲线显示结果如图 5所示,图中红色实线即为核曲线。由图 5中核线的形状可以看出,利用投影轨迹法获取的HRSC影像核线基本接近于直线,这主要是由于火星快车探测器运行比较平稳,在较短的飞行时间内其投影轨迹计算出的核线可近似看作直线。

|
| 图 5 影像范围内投影轨迹法核线结果 Fig. 5 Epipolar Line in Image Area |
虽然HRSC核线整体具有直线性,但是使用一条直线代替由投影轨迹法获取的核曲线仍然会有误差,下文用实验来分析由直线代替核线产生的误差。选取S1影像上、下两端两个像点 p1(1 090.57,15 910.43)、p2(1 035.88,2 174.80)以及中部距离较近的两个像点p3(1 057.65、7 888.51)、p4 (1 057.64,7 885.22),分析核线的斜率K与截距B以及直线拟合后的最大误差err,结果如表 1所示。由表 1可知,4条核曲线使用直线代替的最大误差在1个像素左右,中误差小于1个像素,且4条核线斜率相差很小,因此,在影像范围内HRSC线阵影像的核线具有较好的平行性。
| 编号 | x | y | K | B | err |
| 1 | 1 090.57 | 15 910.43 | 0.001 08 | 746.39 | 0.89 |
| 2 | 1 035.88 | 2 174.80 | 0.001 05 | 746.41 | 0.50 |
| 3 | 1 057.65 | 7 888.51 | 0.001 11 | 746.39 | 1.15 |
| 4 | 1 057.64 | 7 885.22 | 0.001 11 | 746.50 | 1.15 |
采用文献[19]中的线阵影像微分纠正快速算法将原始影像纠正成相对水平影像,计算HRSC影像核线方向,沿核线方向进行重采样,将S1与S2构成红绿立体图像,结果如图 6所示。在红绿立体图像上均匀量测20对同名像点,上下视差最大值为1.2个像素,中误差为0.6个像素。另外,在水平影像上进行核线重采样相当于将原始影像由倾斜摄影转换为正直摄影,可以消除由外方位元素变化引起的几何畸变,更有利于后序影像匹配。

|
| 图 6 HRSC核线影像构成的红绿立体图像(好奇号着陆区—盖尔陨石坑区域) Fig. 6 Epipolar Resampled HRSC Linear Pushbroom Imagery (Gale Creater) |
当前火星探测是深空探测活动的重点,获取 高精度、高分辨率的火星地形数据有助于火星科 学研究以及探测器的精确着陆[20]。本文在利用投影轨迹法分析HRSC线阵影像核线几何关系 的基础上,基于严密几何模型提出了一种实用的HRSC线阵影像近似核线重采样方法,并通过试验验证了算法的可行性。下一步将在本文研究工作的基础上,研究HRSC影像的密集匹配与DSM自动生成技术。
| [1] | Kirk R L, Kraus E H, Rosiek M. Recent Planetary Topographic Mapping at the USGS, Flagstaff: Moon, Mars, Venus, and Beyond[C].The International Conference on Photogrammetry and Remote Sensing, Amsterdam, Netherland, 2000 |
| [2] | Shan J, Yoon J S, Lee D S, et al. Photogrammetric Analysis of the Mars Global Surveyor Mapping Data[J].Photogrammetric Engineering & Remote Sensing, 2005, 71(1) : 97-108 |
| [3] | Rosiek M, Kirk R L, Archinal B A, et al. Utility of Viking Orbiter Images and Products for Mars Mapping[J].Photogrammetric Engineering & Remote Sensing, 2005, 71(10) : 1 187-1 195 |
| [4] | Lbertz J, Gehrke S, Wahlisch M, et al. Digital Cartography with HRSC on Mars Express[C]. The International Archives of Photogrammetry and Remote Sensing, Istanbul, Turkey, 2004 |
| [5] | Albertz J, Attwenger M, Barrett J, et al. HRSC on Mars Express: Photogrammetric and Cartographic Research[J].Photogrammetric Engineering & Remote Sensing, 2005, 71(10): 1 153-1 166 |
| [6] | Geng Xun, Xu Qing, Lan Chaozhen, et al. Martian Surface Topographic Reconstruction Based on Mars Express HRSC Imagery[C]. Deep Space Exploration Conference, Hangzhou, China, 2012(耿迅,徐青,蓝朝桢,邢帅,等.火星快车HRSC影像三维地形重建[C].第九届深空探测学术会议论文集,杭州,中国,2012) |
| [7] | Taejung Kim.A Study on the Epipolarity of Linear Pushbroom Images[J].Photogrammetric Engineering & Remote Sensing, 2000, 66(8): 961-966 |
| [8] | Habib A, Morgan M, Jeong S, et al. Epipolar Geometry of Line Cameras Moving with Constant Velocity and Attitude[J]. ETRI Journal, 2005,27(2):72-180 |
| [9] | Morgan M, Kim K, Jeong S, et al. Epipolar Resampling of Space-Borne Linear Array Scanner Scenes Using Parallel Projection[J]. Photogrammetric Engineering & Remote Sensing, 2006, 72(11):1 255-1 263 |
| [10] | Zhang Zuxun, Zhou Yueqin. A New Approach to Arrange the Approximate Epipolar Lines for SPOT Images[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1989, 14(2): 20-24(张祖勋,周月琴.用拟合法进行SPOT影像的近似核线排列[J].武汉大学学报·信息科学版,1989,14(2): 20-24) |
| [11] | Gong Danchao, Tang Xiaotao, Zhang Li. The Transformation from Tilted Image to Horizontal Image of Line Camera Based on the Rational Function Model[J]. Journal of Geomatics Science and Technology, 2012, 29(4): 240-243(巩丹超,汤晓涛,张丽.基于有理函数模型的线阵CCD遥感影像水平纠正技术[J].测绘科学技术学报,2012, 29(4): 240-243) |
| [12] | Hu Fen, Wang Mi, Li Deren, et al. Approximate Epipolar Rearrangement Algorithm of Satellite Stereo-imagery by Projection Trajectory[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12): 1 431-1 435(胡芬,王密,李德仁,等.利用投影轨迹的卫星影像近似核线重排快速算法[J].武汉大学学报·信息科学版,2009, 34(12): 1 431-1 435) |
| [13] | Hu Fen, Wang Mi, Li Deren, et al. Generation of Approximate Epipolar Images from Linear Pushbroom Satellite Stereo-imagery Based on Projection Reference Plane[J]. Acta Geodaetica et Cargographica Sinica, 2009,38(5):428-436(胡芬,王密,李德仁,等. 基于投影基准面的线阵推扫式卫星立体像对近似核线影像生成方法[J].测绘学报,2009, 38(5): 428-436) |
| [14] | Zhang Yongjun, Ding Yazhou. Approximate Epipolar Image Generation of Linear Array Satellite Stereos with Rational Polynomial Coefficients[J].Geomatics and Information Science of Wuhan University, 2009, 34(9): 1 068-1 071 (张永军,丁亚洲.基于有理多项式系数的线阵卫星近似核线影像的生成[J]. 武汉大学学报·信息科学版,2009,34(9):1 068-1 071) |
| [15] | Zhang Yongsheng, Gong Danchao,Liu Jun, et al. The Application of High Resolution Satellite:the Imaging Model, Processing Algorithm and Application Technology[M]. Beijing: Science Press, 2007 (张永生,巩丹超,刘军,等.高分辨率遥感卫星应用—成像模型、处理算法及应用技术[M].北京:科学出版社,2007) |
| [16] | Duxbury T C, Kirk R L, Archinal B A, et al. Mars Geodesy/Cartography Working Group Recommendations on Mars Cartographic Constants and Coordinate Systems[C].The International Conference on Photogrammetry and Remote Sensing, Ottawa, Canada, 2002 |
| [17] | Acton C. Ancillary Data Services of NASA's Navigation and Ancillary Information Facility[J].Planetary and Space Science, 1996,44(1): 65-70 |
| [18] | Wang Zhizhuo. Principles of Photogrammetry [M]. Wuhan: Wuhan University Press, 2007(王之卓.摄影测量原理续编[M].武汉:武汉大学出版社,2007) |
| [19] | Geng Xun, Xu Qing, Xing Shuai, et al. Differential Rectification of Linear Pushbroom Imagery Based on the Fast Algorithm for Best Scan Line Searching[J]. Acta Geodaetica et Cargographica Sinica, 2013,42(6):861-868 (耿迅,徐青,邢帅,等.基于最佳扫描行快速搜索策略的线阵推扫式影像微分纠正算法[J].测绘学报, 2013,42(6): 861-868) |
| [20] | Xu Qing. Digital Space & Spacial Survey and Its Supporting Techniques[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(2):97-100(徐青.数字空间与深空测绘及其支撑技术[J].测绘科学技术学报,2006, 23(2): 97-100) |
 2015, Vol. 40
2015, Vol. 40


