
文章信息
- 卞玉霞, 刘学军, 甄艳
- BIAN Yuxia, LIU Xuejun, ZHEN Yan
- 三维空间多边形的位置不确定性度量模型
- Uncertainty Measurement Model of Three-Dimensional Polygon
- 武汉大学学报·信息科学版, 2015, 40(1): 26-31
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 26-31
- http://dx.doi.org/10.13203/j.whugis20130174
-
文章历史
- 收稿日期:2013-05-24
空间实体的位置不确定性是GIS的核心研究课题之一,其精度对GIS应用具有较大的影响。对空间实体位置不确定性的研究逐渐引起较多学者的关注[1]。
空间实体包括点、线、多边形(或称GIS面状实体、面元)等类型。点元的位置不确定性在测绘学领域中已有较多的研究,如常用的误差椭圆、误差椭球等。线元的位置不确定性建模是基于误差传播定律、统计学和随机图形学等理论,相继提出了 ε-带模型[2]、置信域模型[3,4]、G-带模型[5]、εσ模型[6]和εm模型[7]、H-带模型[8,9,10,11]、εE模型[12]等,在此基础上,线元的位置不确定性建模也发展了曲线和多边形的位置误差模型等[13,14,15]。线元的位置不确定性模型已经能够较好地评估一般情形下空间线状实体的位置不确定性。多边形的位置不确定性研究已经从模型构建发展到GIS应用[16,17,18,19,20,21,22,23,24],二维空间多边形的位置不确定性研究已经取得了较为丰硕的成果。
空间实体的不确定性研究主要集中在以下几方面:① 二维空间线元、多边形的位置不确定性研究,较少对三维空间实体的位置不确定性进行研究,如三维空间多边形的位置不确定性研究;② 空间实体不确定性的形状刻画,如误差椭圆、哑铃型或棒槌型形状等,较少研究空间实体的误差度量模型。因此,本文以三维空间多边形为研究对象刻画三维空间多边形的位置不确定性形状,并基于积分学原理研究三维空间多边形的位置误差度量模型。 1 三维空间线元置信域模型
线元是由起始端点和终止端点连接而成的,其位置不确定性是由组成线元上所有点(包含线元两端点)的不确定性引起的;而多边形是由其边界线及边界线包围的内点组成的,其位置不确定性是由组成多边形上所有点(包括组成边界线的点)的位置不确定性引起的。线元和多边形的位置不确定性均是由于点元的位置不确定性引起的。三维空间多边形的位置不确定性可以借鉴三维空间线元的位置不确定性等相关理论。因此,本文首先研究三维空间线元的位置不确定性建模过程。
如图 1所示,已知线元两端点P、Q的位置坐标,根据直线参数方程,三维空间线元PQ上待定点R的位置坐标可以表示为:
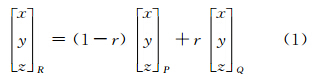
其中r是PR与PQ长度比,r∈ 0,1 。
|
| 图 1 三维空间线元置信域模型 Fig. 1 Confidence Volume Model of Three-Dimensional Line |
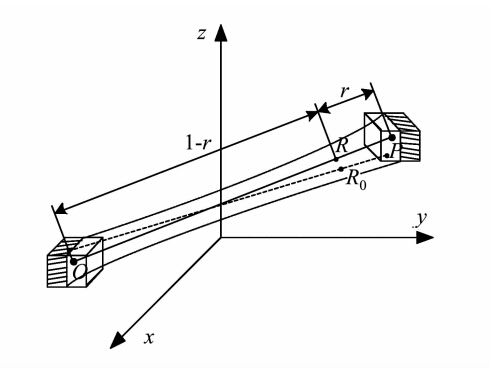
三维空间线元置信域模型是一个将线元真实位置包围在内的三维空间域,是组成线元上所有点元置信域的并集,其大小取决于线元上任意点的位置误差和预设的置信水平。置信水平是线元上所有点的真实位置R0落入相应置信域内的概率。考虑到测绘领域中点位误差服从正态分布,故假设构成线元的点位误差亦服从正态分布,且点位误差在x-y-z各向上相互独立、彼此相等。当线元上所有点的真实位置以不小于预设置信水平的概率落入置信域内时,三维空间线元上任意待定点R的位置误差为[5,8]:
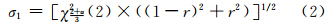
式(2)是以r为自变量、σ1为变量、开口向上的抛物线。当r=0.5时,可以得到σ1的最小值;当r=0或1时,可以得到σ1的两个极大值。由此可以得到三维空间线元的置信域形状(如图 1所示的虚线框围成的区域),该置信域模型为两头大中间小的哑铃型形状。 2 三维空间多边形置信域模型
三维空间多边形置信域模型是一个将多边形真实位置包围在内的三维空间体,是多边形上所有点元置信域的并集。三维空间多边形置信域的大小取决于多边形上任意点的位置误差和预设的置信水平 α,多边形上所有点的真实位置R0(x0,y0,z0)落入相应置信域W内的概率为:

设三维空间多边形上待定点R在x-y-z轴方向上的点位误差分别为σx、σy和σz,多边形上待定点R是满足式(4)的点集。
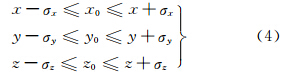
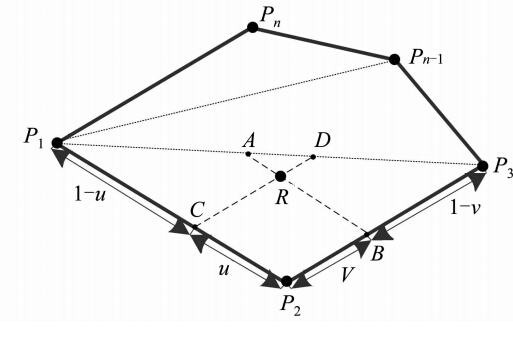
利用三角剖分原理将多边形各顶点连线构建相互邻接且互不重叠的三角形集合。求三维空间多边形上任意点位误差的过程等价于求该点所在三角形上的点位误差。如图 2所示,三维空间多边形P1P2,…,PnP1 ,利用三角剖分原理构造相互邻接且互不重叠的三角形集合P1P2P3 、…、P1Pn-1Pn。
|
| 图 2 三维空间多边形上点位误差 Fig. 2 Position Error of Point on Three-Dimensional Polygon |
图 2所包含的三角形P1P2P3中,AB平行于P1P2,CD平行于P2P3。已知P1C与P2C长度比(1-u)/u及线元两端点位置误差,即可求得P1P2、P1P3上C和D两点的位置误差。根据P3B与P2B长度比(1-v)/v,即可确定RD与CR的长度比(1-v)/v。当确定C、D两点位置误差及RD与CR的长度比的情况下即可求得三维空间多边形上任意点R的位置误差为:

类似地,设首尾相连的三维空间多边形的各点位误差服从正态分布,且各点位误差在x-y-z轴各向上相互独立、彼此相等(σx=σy=σz=σ2)。当多边形上所有点的真实位置以不小于预设置信水平α的概率落入置信域内时,由式(5)及误差传播定律,且仿式(2)可以得到三维空间多边形上任意点R的位置误差:
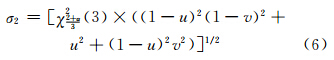
式(6)是以u、v为自变量,σ2为变量的二元高次方程。确定由任意点R组成的三维空间多边形置信域模型可对式(6)求极值。σ2是u、v∈ 0,1 上连续的函数,因此式(6)在u、v∈ 0,1 区间上必定存在极大值和极小值。关于求解式(6)中极大值和极小值的过程,分析如下。
1) 式(6)中,分别对u、v求偏导数。当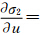 =0及
=0及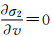 时,可以求得u=1/3,v=1/2为式(6)的驻点坐标。
时,可以求得u=1/3,v=1/2为式(6)的驻点坐标。
2) 为了确定驻点坐标的极值情况,分别对式(6)中u、v求二阶偏导数。此时,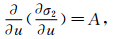
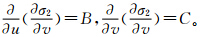
当u=1/3,v=1/2时,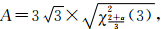
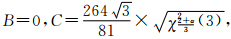 满足A>0,AC-B2>0,该驻点为极小值点。
满足A>0,AC-B2>0,该驻点为极小值点。
3) u=0,v=1或u=1,v=0是式(6)的两端点坐标,即为极值点坐标。当u =0,v=1或u=1,v=0时,式(6)的函数值为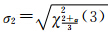 该值大于u=1/3,v=1/2时的函数值
该值大于u=1/3,v=1/2时的函数值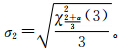 。因此,u=0,v=1或u=1,v=0是极大值点,即可知P1、P2、…、Pn等n个顶点是P1P2,…,PnP1上点位误差最大的点位置。
。因此,u=0,v=1或u=1,v=0是极大值点,即可知P1、P2、…、Pn等n个顶点是P1P2,…,PnP1上点位误差最大的点位置。
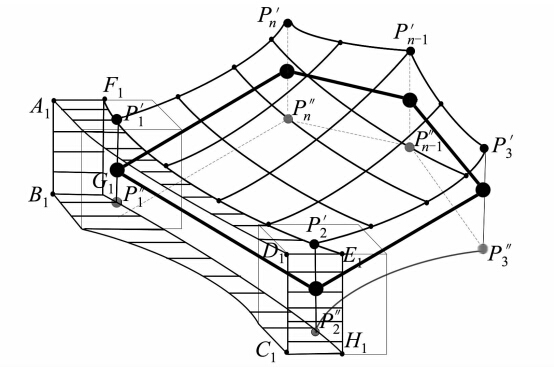
按照上述分析可以得出三维空间多边形的置信域形状如图 3所示,其形状大致为一个上下左右等各个表面均向中间凹陷的凹面体。P1P2…PnP1为三维空间多边形,其置信域模型为凹面体P′ 1P″ 1P′ 2P″ 2…P′ nP″ nP′ 1P″ 1及P1P2…PnP1各个边界的置信域围成的空间域。其中,P′ 1P′ 2…P′ nP′ 1是四周向中心平滑凹陷的凹面,且P′ 1P′ 2…P′ nP′ 1与P″ 1P″ 2…P″ nP″ 1基于多边形P1P2…PnP1对称;A1B1C1D1E1F1G1是线段P1P2形成的两端大、中间小的哑铃型三维空间置信域,其他线目标(如P2P3、…、Pn-2Pn-1、PnP1等)形成的置信域形状与P1P2的置信域形状类似。
|
| 图 3 三维空间多边形置信域模型 Fig. 3 Confidence Domain Model of Three-Dimensional Polygon |
如图 3所示,三维空间多边形置信域模型值T由0.5倍边界线上点元置信域集合和多边形所有内点置信域集合两部分组成。由于三维空间边界线上所有点元置信域集合对三维空间多边形置信域影响较小,可以忽略0.5倍边界线上点元置信域集合对三维空间多边形置信域的影响。
基于三角剖分原理研究多边形内点所在三角形上的点位误差是构建三维空间多边形置信域模型的基础。因此,度量三维空间多边形置信域模型是计算剖分形成的各三角形置信域并集的过程。
三维空间三角形置信域模型是以三角形为对称面,以 σ2为厚度的相互对称的凹面体。为了便于计算,该置信域模型可以描述为:以三角形面积作为闭区域D,以Z=2σ2作为高的三维空间体。考虑到该三维空间体中σ2是变化的量,因此三维空间三角形置信域T1采用多元函数积分学原理进行度量。
结合式(6),三维空间体的高度函数Z可以表示为:

将闭区域D任意划分为n个小区域,在每个小区域上任意取一点(ui,vi),作函数f(ui,vi)与小区域面积Δωi的乘积,并作和:
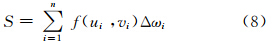
当闭区域D被划分为无穷多个小区域,S趋于极限值时,该极限值即为三维空间三角形的置信域T1,它可以用函数f(u,v)在闭区域D上的定积分表示:
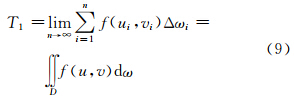
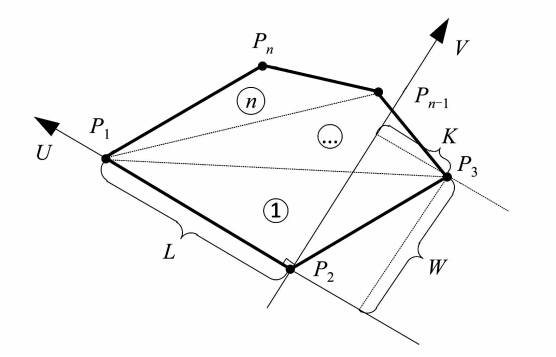
构建如图 4所示的坐标系uP2v,该坐标系是以三角形所包含多边形的一条边界线P1P2为u轴,并以该边界线的端点P2为坐标原点,以另一顶点P3到u轴的垂直方向为v轴。三角形P1P2P3中,已知P1P2的长度为L,P3到P1P2的垂距为W,P3到v轴的距离为K。根据已知条件可以计算P1P3和P2P3在直角坐标系中的方程。由此,积分区域D可以表示为:
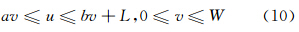
设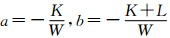 。同时也需要注意,当P3与P1、P2位于同一象限时,
。同时也需要注意,当P3与P1、P2位于同一象限时,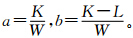
|
| 图 4 三维空间多边形的置信域度量 Fig. 4 Confidence Volume Measurement of Three-Dimensional Polygon |
根据式(7)、式(10)及直角坐标计算二重积分方法,可以将式(9)转化为:
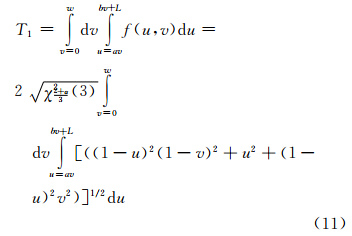
三维空间多边形P1P2…PnP1置信域T是组成该多边形的相互邻接且互不重叠的n个三角形置信域的并集,故三维空间多边形置信域度量模型可以表示为:
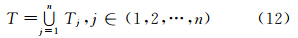
其中,Tj表示剖分形成的第j个多边形的置信域。 4 实例验证
建筑物面积误差是指建设工程竣工时实测总建筑面积超出规划许可的总建筑面积部分,它是由于建筑物各表面投影到某一空间平面上的位置误差引起的。本文以工程中建筑物面积误差为例,度量建筑物地面的置信域模型,评估三维空间多边形位置不确定性对建筑物面积误差的影响。
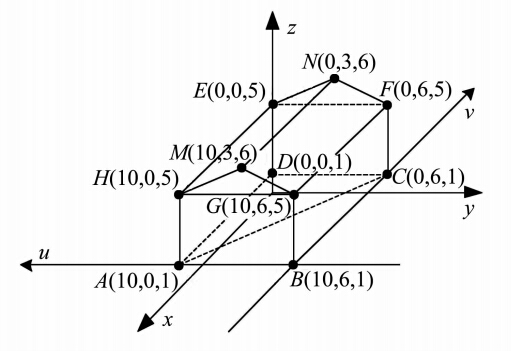
构建由A(10,0,1)、B(10,6,1)、C(0,6,1)、D(0,0,1)、E(0,0,5)、F(0,6,5)、G(10,6,5)、H(10,0,5)、M(10,3,6)、N(0,3,6)等坐标点依次相连围成如图 5所示的建筑物,建筑物面积是指由A、B、C、D围成的空间多边形ABCD的面积。由于ABCD的位置不确定性会导致建筑物面积误差。 因此,度量建筑物面积误差的问题可归结为三维空间多边形的位置不确定性度量问题。
|
| 图 5 建筑物 Fig. 5 Building |
由已知点位A、B、C、D构成的多边形ABCD中,这些点位误差服从正态分布,且各个点位误差相互独立、彼此相等。在满足以上条件的情况下,根据式(6)可知,三维空间多边形上点位误差为:
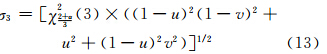
将ABCD通过三角剖分原理划分为相互邻接且互不重叠的三角形集合,即三角形ABC和三角形ACD。根据式(11)所示的三维空间三角形的置信域度量模型,度量各个三角形的置信域值。如三角形ABC中,线段AB是多边形的一条边界线,L=6,该三角形中顶点C到线段AB的距离为10,则W=10。在以B为中心、AB为u轴、BC为v轴的临时坐标系uBv中,C到v轴的距离为0,即K=0。当预设置信水平α=95%时,χ20.983(3)=10.2,利用Matlab 7.0中quad2d函数进行双重定积分求得三维空间多边形 ABC的置信域约等于0.9。同理求得ACD的置信域,根据式(12)可以求得建筑物面积误差T约为1.8。
为了更好地表达测量结果,通常用相对误差表示测量值的精度,则房屋面积的相对误差为T与建筑物面积的比值。在ABCD 上所有点的真实位置以不小于预设置信水平95%的概率落入置信域内时,建筑物面积相对误差约为3%。
《浙江省城镇建设工程竣工规划核实管理办法》中规定建筑物面积最大合理误差是3%,与本文实例推导结果基本一致。由此可见,三维空间多边形的置信域度量模型可用于工程建设等领域的质量控制过程。 5 结 语
本文在分析三维空间线元位置不确定性的基础上,提出了三维空间多边形置信域模型,基于积分学原理构建了三维空间多边形置信域度量模型。
需要注意的是,本文研究是在构成三维空间多边形的点位误差服从正态分布,点位误差在x-y-z各向上相互独立、彼此相等的情况下进行的研究。对于相互关联的三维空间点元构成的多边形的位置不确定性还需要进一步探讨。
| [1] | Abler R F. The National Science Foundation National Center for Geographic Information and Analysis[J]. International Journal of Geographical Information System, 1987, 1(4): 303-326 |
| [2] | Chrisman N. A Theory of Cartographic Error and its Measurement in Digital Data Bases[C]. American Congress on Surveying and Mapping, Bethesda,1982 |
| [3] | Shi W. A Generic Statistical Approach for Modeling Error of Geometric Features in GIS [J]. International Journal of Geographical Information Science, 1998, 12(2): 131-143 |
| [4] | Shi Wenzhong. The Stochastic Process Model for Handling Positional Uncertainty of Line Segments in GIS[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(1): 37-44(史文中. GIS中线元位置不确定性的随机过程模型[J]. 测绘学报, 1998, 27(1): 37-44) |
| [5] | Shi W, Liu W.A Stochastic Process-Based Model for the Positional Error of Line Segments in GIS [J]. International Journal of Geographical Information Science, 2000, 14 (1): 51-66 |
| [6] | Zhu Changqing, Zhang Guoqin, Shi Wenzhong. Algebraic Research on Geometrical Characteristic of Error Band for 2D Linear Segment Uncertainty ε_σ Model[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 463-467(朱长青, 张国芹, 史文中. 二维线元不确定性ε_σ模型误差带几何特征的代数研究[J]. 测绘学报, 2007, 36(4): 463-467) |
| [7] | Zhang Guoqin,Zhu Changqing,Li Guozhong. Measurement Indexes of Positional Uncertainty for Plane Line Segment Based on ε_m Model[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 431-435(张国芹, 朱长青, 李国重. 基于ε_m模型的线元位置不确定性度量指标[J]. 武汉大学学报·信息科学版, 2009, 34(4): 431-435) |
| [8] | Fan Aimin, Guo Dazhi. The Uncertainty Band Model of Error Entropy[J], Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 48-53(范爱民, 郭达志. 误差熵不确定带模型[J]. 测绘学报, 2001, 30(1): 48-53) |
| [9] | Li Dajun, Gong Janya, Xie Gangsheng, et al. Error Entropy Band for Linear Segments in GIS[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5): 462-465(李大军, 龚健雅, 谢刚生, 等. GIS中线元的误差熵带研究[J]. 武汉大学学报·信息科学版, 2002, 27(5): 462-465) |
| [10] | Zhu Changqing, Zhang Guoqin, Wang Guangxia. An Error Entropy Model for GIS Spatial Linear[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 405-407(朱长青,张国芹,王光霞. GIS中三维空间直线的误差熵模型[J]. 武汉大学学报·信息科学版, 2005, 30(5): 405-407) |
| [11] | Shi Yufeng, Shi Wenzhong, Jin Fengxiang. Hybrid Entropy Model of Spatial Data Uncertainty in GIS[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 82-85(史玉峰,史文中,靳奉祥. GIS中空间数据不确定性的混合熵模型研究[J]. 武汉大学学报·信息科学版, 2006, 31(1): 82-85) |
| [12] | Zhang Guoqin,Zhu Changqing,Li Guozhong. A Positional Uncertainty ε_E Model for Line Segment Considering Error Ellipse Long Semi-axis as Error Band Width[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 495-499(张国芹, 朱长青,李国重. 以误差椭圆长半轴表示带宽的线元位置不确定性ε_E模型[J]. 武汉大学学报·信息科学版, 2010, 35(4): 495-499) |
| [13] | Shing Wenzhong, Tong Xiaohua, Liu Dajie. An Approach for Modeling Error of Generic Curve Features in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(1): 52-58(史文中, 童小华, 刘大杰. GIS中一般曲线的不确定性模型[J]. 测绘学报, 2000, 29(1): 52-58) |
| [14] | Liu Chun, Shi Wenzhong, Liu Dajie . Relationship of Uncertainty Between Polygon Segment and Line Segment for Spatial Data in GIS[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1): 65-68(刘春, 史文中, 刘大杰. GIS空间数据面元与线元不确定性的关系[J]. 武汉大学学报·信息科学版, 2005, 30(1): 65-68) |
| [15] | Tang Zhong'an, Shi Wenzhong. Equivalent Probability Density Error Model to 2D Generic Curve in Vector GIS[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 85-89 (汤仲安, 史文中. 矢量GIS平面一般曲线等概率密度误差模型[J]. 武汉大学学报·信息科学版, 2007, 32(1): 85-89) |
| [16] | Liu Wenbao, Dai Honglei, Xu Panlin, et al. The Model of Planar Polygon's Positional Error Donut in GIS[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(4): 338-344(刘文宝, 戴洪磊, 徐泮林, 等. GIS中平面面位误差环的解析模型[J]. 测绘学报, 1998, 27(04): 338-344) |
| [17] | Li Dajun, Gong Jianya, Xie Gangsheng, et al. The Model of Error Entropy of Area Unit in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 31-35(李大军, 龚健雅, 谢刚生, 等. GIS中面元的误差熵模型[J]. 测绘学报, 2003, 32(1): 31-35) |
| [18] | Ort P A J, Stein A, Bregt A K, et al. A Variance and Covariance Equation for Area Estimates with a Geographic Information System[J]. Forest Science, 2005, 51(4): 347-356 |
| [19] | Chen Jianjun, Zhou Chenghu, Cheng Weiming. Area Error Analysis of Vector to Raster Conversion of Areal Feature in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 344-349(陈建军, 周成虎, 程维明. GIS中面状要素矢量栅格化的面积误差分析[J]. 测绘学报, 2007, 36(3): 344-349) |
| [20] | Delafontaine M, Nolf G, van de Weghe N, et al. Assessment of Sliver Polygons in Geographical Vector Data[J]. International Journal of Geographical Information Science, 2009, 23(6): 719-735 |
| [21] | Jung Y, Merwade V. Uncertainty Quantification in Flood Inundation Mapping Using Generalized Likelihood Uncertainty Estimate and Sensitivity Analysis[J]. Journal of Hydrologic Engineering, 2011, 17(4): 507-520 |
| [22] | Luoto M, Marmion M, Hjort J. Assessing Spatial Uncertainty in Predictive Geomorphological Mapping: A Multi-Modelling Approach[J]. Computers & Geosciences, 2010, 36(3): 355-361 |
| [23] | Chen H, Wood M D, Linstead C, et al. Uncertainty Analysis in a GIS-based Multi-criteria Analysis Tool for River Catchment Management[J]. Environmental Modelling & Software, 2011, 26(4): 395-405 |
| [24] | Wei R, Murray A T. An Integrated Approach for Addressing Geographic Uncertainty in Spatial Optimization[J]. International Journal of Geographical Information Science, 2012, 26(7): 1 231-1 249 |
 2015, Vol. 40
2015, Vol. 40




