文章信息
- 卢骏, 戴吾蛟, 章浙涛
- LU Jun, DAI Wujiao, ZHANG Zhetao
- 大坝变形变系数回归建模
- Modeling Dam Deformation Using Varying Coefficient Regression
- 武汉大学学报·信息科学版, 2015, 40(1): 139-142
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 139-142
- http://dx.doi.org/10.13203/j.whugis20130305
-
文章历史
- 收稿日期:2014-07-08
2. 湖南省精密工程测量与形变灾害监测重点实验室, 湖南 长沙, 410083;
3. 湖南地科资源利用工程设计有限公司, 湖南 长沙, 410007
2. Key Lab of Precise Engineering Surveying & Deformation Disaster Monitoring of Hunan Province, Changsha 410083, China;
3 Resource Utilization and Engineering Design of Earth Science Corporation, Changsha 410007, China
回归分析是变形建模中一种常用的物理统计建模方法,它是通过建立变形影响因素与变形量之间的数学关系式,即回归方程,然后利用所建立的回归方程来对变形体的变形进行分析以及预报[1, 2]。但是,普通回归分析是一种静态模型,即模型一旦建立,变形量与变形影响因素之间的函数关系保持不变[3]。但在实际应用中,变形体的结构或物理性质将随着时间的推移或周边环境的变化而发生变化,这样,利用普通线性回归而建立的回归方程将不再适用。为了克服普通回归分析建模的这一弊端,将变系数回归分析模型引入变形分析建模中。该模型通过假定线性回归模型中的回归系数是其他自变量的未知函数,是一种动态模型,从而增加了模型的灵活性和适应性。本文在介绍变系数回归模型的基础上,对其估计方法进行探讨,然后通过仿真和实际大坝监测数据建模分析,以验证变系数回归在大坝变形建模中的有效性和实用性。
1变系数模型及其拟合方法
变系数模型是通过假定线性回归模型的回归系数为另一自变量 U的未知函数的模型。设Y为因变量,X1,X2,…,Xp和U为自变量,若Y与X1,X2,…,Xp及U满足:
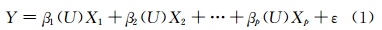
其中,βj(·)(j=1,2,…,p)为未知函数;ε为误差项,且E(ε|U,X1,…,Xp)=0, Var(ε|U,X1,…,Xp)=σ2(U),则模型被称为变系数回归模型[4]。
变系数回归主要的拟合方法有三种:核光滑估计方法、多项式样条估计方法以及光滑样条估计方法[5, 6, 7]。由于变系数模型本质上还是局部线性模型,因此更适合于用局部光滑方法来拟合。在实际应用中,较为常用的是局部线性拟合[7, 8],其具体算法如下所示。
设(Yi,Xi1,…,Xip,Ui)(i=1,2,…,n)为n组独立的观察数据,则变系数模型的样本形式为:
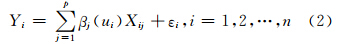
式中,βj(u)(j=1,2,…,p)为关于u连续的导数,μ为u的取值范围。对任意给定的u0∈μ,由Taylor公式,在u0的邻域内有:
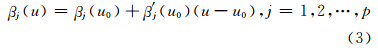
设K(t)为给定的核函数[8, 9],且Kh(t)=K(t/h)/h,则变系数模型的局部线性拟合即选择βj(u0)和β′ j(u0)使得:
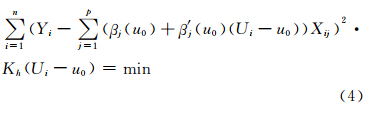
令
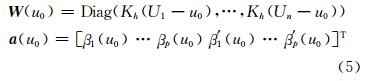
则上述加权最小二乘问题的解可以表示为:
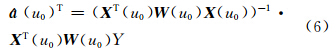
因此系数函数向量 β (u)= T在u0处的局部线性估计可以表示为:
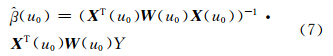
因此可得因变量Y在各设计点Ui(i=1,2,…,n)的拟合值为:
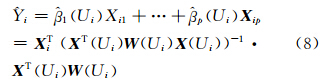
其中,X Ti= 为X1,X2,…,Xp的第i组观测值。
2仿真数据分析
模拟实验取的变系数模型为Y=β1(U)X1+β2(U)X2,模型系数函数如式(9)所示:
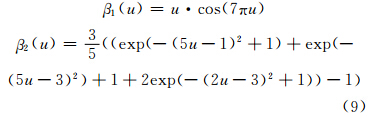
令U、X1、X2分别服从均匀分布U(0,1)、U(0,2)、U(0,3),独立随机抽取了容量为500的随机样本,并利用已知的变系数模型计算Y的取值。由于实际应用中Y、X1、X是通过观测得到的,因此,Y、X1、X的取值再加上服从标准正态分布N(0,1)的误差项ε。然后采用局部线性拟合法进行变系数回归,并与普通的线性回归模型进行比较。
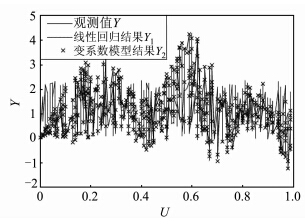
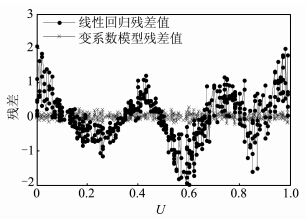
图 1为变系数回归模型与普通线性回归模型的结果比较,其中,实线条表示观测值Y,虚线条表示普通线性回归结果,X形标记表示变系数回归结果。图 2为两种回归模型的回归残差,其中,圆点标记的线条表示线性回归模型回归残差序列,X形标记的线条表示变系数回归模型回归残差序列。同时,线性回归模型回归结果的中误差为0.833 5,而变系数回归模型回归结果的中误差为0.083 7。由图 1、2及两种回归模型回归结果的中误差可知,变系数回归建立的模型比普通线性回归建立的模型更准确。
|
|
图 1 不同模型回归结果与真值的比较图
Fig. 1 Different Regression Results Compare with the True Value |
|
| 图 2 不同模型的残差值比较图 Fig. 2 Residuals of Different Regression Models |
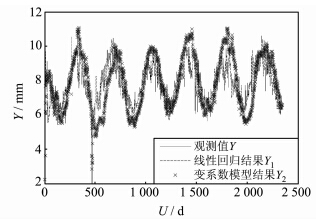
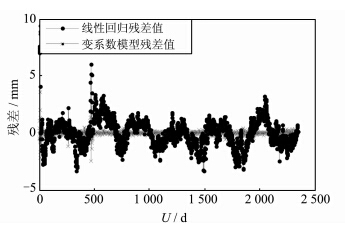
实例数据为五强溪大坝2004\|04\|01~2010\|09\|01总共2 345 d的监测数据,包括大坝引张线向下形变量以及影响因子(降雨量、水位和温度)的观测数据。采用的变系数模型为 Y=β1(U)X1+β2(U)X2+β3(U)X3,其中,Y为位移量,X1、X2、X3分别表示降雨量、水位、和温度3个影响因子,U为时间。实验利用变系数回归与普通线性回归对5个监测点进行建模,图 3和图 4为其中1号点的建模结果。图 3中,实线条表示观测值Y(即大坝向下形变量),虚线条表示普通线性回归结果,X标记表示变系数回归结果。图 4中,点状线条表示普通线性回归残差值,X形线条表示变系数回归残差值。表 1为5个点两种回归建模得到的回归残差序列的RMS值。从图 3、4及表 1中可以看出,变系数回归建立的变形模型比普通线性回归建立的模型更准确。
|
| 图 3 不同模型回归结果与真值的比较图 Fig. 3 Different Regression Results Compare with the True Value |
|
| 图 4 不同模型的残差值比较图 Fig. 4 RMS for Residuals in Different Regression Models/mm |
| 回归模型 | 1号点 | 2号点 | 3号点 | 4号点 | 5号点 |
| 线性回归模型 | 0.681 0 | 0.625 9 | 1.357 5 | 2.923 4 | 1.207 6 |
| 变系数回归模型 | 0.122 8 | 0.107 2 | 0.307 2 | 1.021 3 | 0.202 8 |
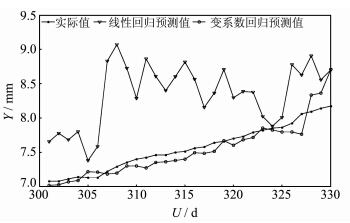
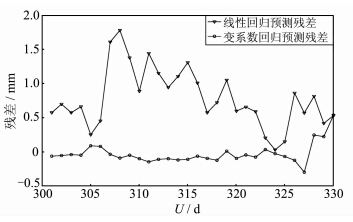
为了进一步说明变系数回归模型的优越性,又选取了其中300 d的观测数据,分别利用普通 线性回归与变系数回归进行建模,并对其后30 d 进行预报,然后将预报值与实际观测值进行比较。 图 5为两种模型的预测值以及实际变形观测值的序列图,其中,点状标记的线条表示实际值,圆型标记的线条表示变系数回归模型预报值,倒三角标记的线条则表示线性回归模型预报值。图 6为两种模型预测值减去实际变形观测值而得到的残差序列图,其中,倒三角标记的线条表示线性回归模型预测值残差,圆型标记的线条表示变系数回归模型预测值残差。表 2为5个点的两种回归模型预测残差序列的RMS值。可以看出,变系数 回归模型的预测残差远小于线性回归模型预测残差,说明变系数回归模型具有更准确的预报能力。
|
| 图 5 不同模型预测值同实际值比较图 Fig. 5 Predictive Value Compare with True Value in Different Regression Models |
|
| 图 6 不同模型预测结果残差比较图 Fig. 6 Prediction Residuals of Different Regression Models |
| 回归模型 | 1号点 | 2号点 | 3号点 | 4号点 | 5号点 |
| 线性回归模型 | 0.279 7 | 0.260 6 | 0.429 1 | 1.190 2 | 0.478 3 |
| 变系数回归模型 | 0.047 3 | 0.047 5 | 0.214 5 | 0.779 8 | 0.162 4 |
当因变量与自变量间的函数关系随着某个因子的变化而变化时,变系数回归模型可以很好解决这一问题。从大坝变形的变系数回归建模可以看出:① 水位、温度及降雨对大坝变形影响是变化的,说明实践应用中变形影响因子对大坝变形的影响是非线性的;② 利用变系数回归建立的大坝变形模型能更好地适应变形影响因子的这种非线性的影响,具有更准确的预报能力,更符合实践应用的需要。
| [1] | Lu Li, Xu Jianxuan. Regression Analysis Methods of Building Deformation Monitoring[J]. Geotechnical Investigation and Surveying, 2004(5): 17-19(陆立, 许建宣. 建筑物变形监测的回归分析法[J]. 工程勘察, 2004(5): 17-19) |
| [2] | Xu Hui, Li Gang. BP Neural Network Based on Matlab Applied in Dam Observation Data Processing[J]. Geomatics and Information Science of Wuhan University, 2005, 30(3): 50-53(徐晖, 李钢. 基于Matlab的BP神经网络在大坝观测数据处理中的应用[J]. 武汉大学学报·信息科学版, 2005, 30(3): 50-53) |
| [3] | Green P J, Silverman B W. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach[M]. London: Chapman and Hall, 1994 |
| [4] | Fan J, Zhang W. Statistical Estimation in Varying Coefficient Models[J]. Ann Statist, 1999,27: 1 491-1 518 |
| [5] | Fan J, Zhang W. Simultaneous Confidence Bands and Hypothesis Testing in Varying Coefficient Models[J]. Scand J Statist, 2000, 27: 715-731 |
| [6] | Tang Qingguo, Cheng Longsheng. B-spline Estimation for Varying Coefficient Regression with Spatial Data[J]. Science in China Series A: Mathematics, 2009, 52(11): 2 321-2 340 |
| [7] | Mei Changlin, Wang Ning. Modern regression Analysis Methods[M]. Beijing: Scientific Press, 2012(梅长林, 王宁. 近代回归分析方法[M]. 北京:科学出版社, 2012) |
| [8] | Lu Yiqiang. Research and Analysis of Varying Coefficient Model[D]. Shanghai: East China Normal University, 2003(卢一强. 变系数模型的研究与分析[D]. 上海: 华东师范大学, 2003) |
| [9] | Tang Qingguo, Wang Jinde. One Step Estimation Methods of Varying Coefficient Model[J]. Science in China Series A: Mathematics, 2005, 35(1): 23-38(唐庆国, 王金德. 变系数模型中的一步估计法[J]. 中国科学A辑, 2005, 35(1): 23-38) |
 2015, Vol. 40
2015, Vol. 40


