文章信息
- 翟振和, 王兴涛, 李迎春
- ZHAI Zhenhe, WANG Xingtao, LI Yingchun
- 解析延拓高阶解的推导方法与比较分析
- Solution and Comparison of High Order Term of Analytical Continuation
- 武汉大学学报·信息科学版, 2015, 40(1): 134-138
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 134-138
- http://dx.doi.org/10.13203/j.whugis20130155
-
文章历史
- 收稿日期:2014-05-20
2. 西安测绘研究所, 陕西 西安, 710054;
3. 大地测量与地球动力学国家重点实验室, 湖北 武汉, 430077
2. Xi'an Institute of Surveying and Mapping, Xi'an 710054, China;
3. State Key Laboratory of Geodesy and Earth's Dynamics, Wuhan 430077, China
解析延拓思想是物理大地测量的重要基础理论之一,在边值问题求解、高精度大地水准面确定、重力数据向下延拓等方面有着重要作用[1, 2, 3, 4, 5, 6]。解析延拓解的零阶项是地面重力异常本身,其一阶项g1的计算涉及到重力异常的一阶导数,文献[7]提出了计算g1项的小波算法,该算法具有快速、准确的特点,特别适用计算大范围g1项的值。文献[8]利用位于参考平面上的无限延伸的三棱质体模型检验了解析延拓解(至一阶项)和借助地形数据解在解算垂线偏差时的精度。文献[9]论证了Moritz解析延拓解与Bjerhammar虚拟球面解的等价性。而对于二阶或更高阶的计算,少有文献给出具体的推导和计算分析,因此,本文利用传统思路以及新的推导思路给出解析延拓解的高阶解的推导方法,并以重力异常的解析延拓为例进行计算和比较分析。
1 解析延拓的递推解
假设在解析延拓中将一点 p的重力异常ΔgP延拓至对应该点的水准面得到Δg′ p。
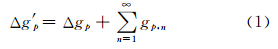
其中,
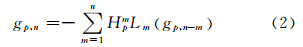
式中,L表示垂线方向导数算子。
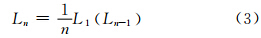
Hp表示点p相对于该水准面的高度,gp,2项的表达式为:

对于g2、g3等高阶项的计算,文献[10, 11]推荐使用递推算法,即首先计算L1 Δgp ,L1 Δgp 即重力异常的径向导数,其计算公式如下[11]。
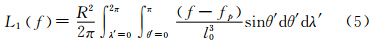
式中,l0=2Rsin ψ 2 。利用该式得到:
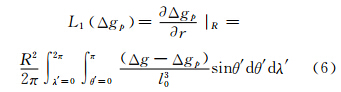
L2 ΔgP 的计算按照式(3)得:
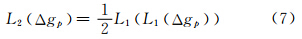
L1 gp,1 的计算式为:

综合以上推导可得到解析延拓g2项的表达式:

对g3等高阶项的计算也可以仿照以上思路进行。在实际计算中,递推算法的主要问题是计算高阶项时,需要的重力数据范围不断扩大,增加了计算复杂度和工作量。当球面角距ψ→0时,文献[10]指出式(5)的奇异性被中和了,然而从数学角度严格分析,实际上当ψ→0时,式(5)中 →∞,(f-fp) →0,严格意义上,这种奇异在理论上并没有消除,或者说无法从理论上具体讨论
→∞,(f-fp) →0,严格意义上,这种奇异在理论上并没有消除,或者说无法从理论上具体讨论 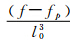 的极限和变化趋势,因此,在理论上解决其奇异问题具有很大难度。
2 迭代求导法
的极限和变化趋势,因此,在理论上解决其奇异问题具有很大难度。
2 迭代求导法
由经典理论可知,球外一点的谐函数Vp(r,θ,λ)可表示为:
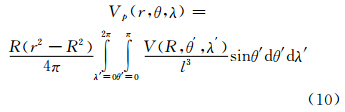
Vp(r,θ,λ)的径向导数可由球面上的球谐函数值V(R,θ′,λ′)求得,公式为:

由调和函数性质可以得出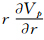 也为调和函数,因此也满足式(11),将
也为调和函数,因此也满足式(11),将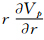 代入式(11)得到:
代入式(11)得到:
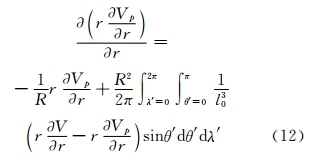
球近似后,进而得到球面上的二阶径向导数:

仿照以上思路,将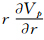 代入式(13),可以得到球谐函数的三阶及更高阶的径向导数。
代入式(13),可以得到球谐函数的三阶及更高阶的径向导数。
考虑rΔgp为调和函数,因此可将其代入式(13)得到重力异常径向二阶导数在球近似时的值。
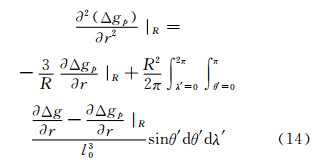
考虑到
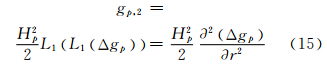
将式(15)代入式(14)可以得到解析延拓g2项:
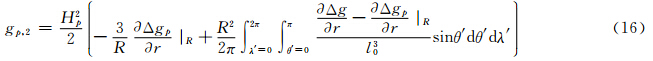
从以上推导可以看出,g3等更高阶的计算都需要先计算更高阶的重力异常导数,由于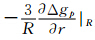 数值很小,利用上述迭代法求导在忽略小项影响后,重力异常径向导数可表述为:
数值很小,利用上述迭代法求导在忽略小项影响后,重力异常径向导数可表述为:
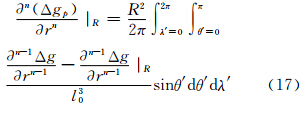
如果忽略(17)中的小项,则迭代求导法获得的解析延拓解与递推方法获得的解析延拓解在忽略小项影响后,可以认为是等价的。由于迭代求导的思想在理论上是严密的,因此文献[10, 11]中利用式(9)进行递推求解其实也是进行了近似,但这种近似并不影响实际计算的精度。另一方面也可以看出Molodensky边值问题中的解析延拓解本质上可以归结为求解重力异常在垂线方向上的各阶导数。
3 直接求导法
将式(10)两边视为r的函数,令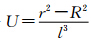 ,则式(10)两边同时对r求二阶导数得:
,则式(10)两边同时对r求二阶导数得:

引入特殊的球谐函数VS(r,θ,λ)=  ,同时求解的二阶导数为:
,同时求解的二阶导数为:

由于VS(r,θ,λ)|R=1,因此将式(19)代入式(18)得到:

(20)两边分别乘VP,并用式(18)减去其得:
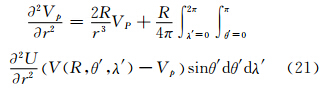
当进行球近似时:
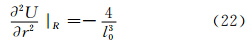
由此得到球谐函数二阶径向导数在球面上的值:

考虑到rΔgp为调和函数,将其代入式(23)得到重力异常的二阶导数:

进而得到:

利用上式可以得到解析延拓gp,2项:

式(26)即利用直接求导思想获得的解析延拓gp,2项。从以上推导可以看出,直接求导法获得的解析延拓高阶解的形式与递推法、迭代法并不一致,最大的区别在于直接求导法并不需要重力异常径向导数参与积分运算。对于其他高阶项的计算也可以仿照以上思路进行。
4 计算分析
为了比较三种推导方法的差异,本文以解析延拓解中g2项的计算作为分析对象。实验区域重力和地形数据范围为5°×5°,重力数据分辨率为2.5′,解析延拓区域范围为实验区中心的1°×1°区域,延拓高度为计算点的高程,延拓区域地形(由 SRTM30"数据格网化得到)和重力异常数据(由EGM2008模型得到)分布分别见图 1、图 2。

|
| 图 1 延拓区域5°×5°地形 Fig. 1 Terrain of 5°×5° Continuation Area |

|
| 图 2 延拓区域1°×1°地面重力数据 Fig. 2 Land Gravity Data of 1°×1° Continuation Area |
本文的计算重点在于考察相同数据范围下不同推导方法带来的实际影响,g1项的计算对于三种方法都是一样的,其变化范围是-4 mGal~19 mGal,如图 3所示。图 4为递推法和迭代方法获得的g2项(变化范围是-0.4 mGal~2.3 mGal),图 5为直接求导方法获得的g2(变化范围是-0.3 mGal ~1.9 mGal)。

|
| 图 3 延拓区域1°×1°的g1 Fig. 3 g1 Term of Analytical Continuation of Continuation Area |

|
| 图 4 递推方法和迭代方法获得的g2 Fig. 4 g2 Term Derived from Iterative Derivative Method and Recursion Method |

|
| 图 5 直接求导方法获得的g2 Fig. 5 g2 Term Derived from Direct Derivative Method |
对比图 5和图 4可以看出,直接求导法获得的g2项与经典递推法、迭代求导法获得的g2项整体趋势一致,但量级要偏小,整体上偏小0.1~0.4 mGal。理论上分析,直接求导法与递推法、迭代求导法应是等价的,但直接求导法在实际计算时,重力异常低阶导数在计算高阶项时并不参与积分运算,由于积分运算在局部区域本身存在一定的计算误差,因此,不同方法间的差异更多的是由于实际计算的误差引起的。
5 结 语
针对Molodensky边值问题中解析延拓高阶解的求解,利用迭代求导法、直接求导法对解析延拓高阶解进行了推导,获得了高阶解的理论公式。通过比较分析发现,迭代法获得的高阶解是严密的,而递推法实际上忽略了数值上小项的影响,在忽略小项后,迭代法与递推法是严格等价的。
利用5°×5°实验区的重力数据求解了核心区域1°×1°重力数据的g1、g2项,通过计算发现直接求导法获得的g2项数值与经典方法相比偏小0.1~0.4 mGal。直接求导法由于积分运算的减少,因此计算速度较其他方法要快,但在实际计算 中由于计算误差的影响,其结果与其他方法并不一致,这种差异的消除需要进一步论证分析。
致谢:感谢61081部队张传定高级工程师给予专业问题上的指导和帮助。
| [1] | Cao Huasheng, Zhu Zhuowen, Yu Jinhai. Poisson Boundary Value Problem[J].Journal of Wuhan Technical University of Surveying and Mapping,1999,24(1):1-18 (操华胜,朱灼文,于锦海.Poisson重力边值问题[J]. 武汉测绘科技大学学报, 1999,24(1):1-18) |
| [2] | Wang Dan, Li Hui, Shen Chongyang, et al.Upward Continuation of Ground Gravity Space-Time Change to Satellite Altitude[J].Journal of Geodesy and Geodynamics. 2005,25(2):69-71 (王丹,李辉,申重阳,等.地面重力时空变化向卫星高度的解析延拓[J]. 大地测量与地球动力学,2005,25(2):69-71) |
| [3] | Fei Zhiling. Refinements of Geodetic Boundary Value Problem Solutions[D]. Canada:University of Calgary,2000 |
| [4] | Shi Pan, Sun Zhongmiao. The Solution to the Problem of the Spherical Interior Dirichlet and Its Application[J]. Acta Geodaetica et Cartographic Sinica, 1999,28(3):195-198(石磐,孙中苗.球内Dirichlet 问题解及其应用[J].测绘学报,1999,28(3):195-198) |
| [5] | Zhang Chuanyin, Dang Yamin, Ke Baogui, et al. Discussion of Some Issues in the Coastal Precise Quasi-Geoid Determination[J]. Geomatics and Information Science of Wuhan University, 2012,37(10): 1 150-1 154 (章传银,党亚民,柯宝贵, 等.高精度海岸带重力似大地水准面的若干问题讨论[J].武汉大学学报·信息科学版. 2012,37(10):1 150-1 154) |
| [6] | Shen Wenbin, Yan Jianguo, Chao Dingbo. Local Fictitious Downward Continuationof Gravity Field and Simulation Experiment Tests Using EGM96 Model[J]. Geomatics and Information Science of Wuhan University, 2006,31(7):589-592 (申文斌,鄢建国,晁定波.重力场的局部虚拟向下延拓以及利用EGM96模型的模拟实验检验[J]. 武汉大学学报·信息科学版.2006,31(7):589-592) |
| [7] | Yu Jinhai, Zhu Zhuowen, Peng Fuqing. The Wavelet Algorithm of g1 Term Computation in Molodensky Boundary Value Problem[J].Chinese Journal of Geophysics, 2001,44(1):113-115 (于锦海,朱灼文,彭富清.Molodensky边值问题中解析延拓法g1项的小波算法[J].地球物理学报,2001,44(1):113-115) |
| [8] | Sheng Zongqi. Analytical Continuation Solution and Model Test Using Terrain Data[J]. Journal of Institute of Surveying and Mapping, 1989(1):11-15 (盛宗琪.解析延拓解及借助地形数据解的模型检验[J].测绘学院学报,1989(1):11-15) |
| [9] | Cheng Luying, Xu Houze. Equivalence Between Moritz Analytical Continuation and Bjerhammar Virtual Spherical Solution[J]. Hydrographic Surveying and Charting,2008,28(3):6-9 (程芦颖,许厚泽. Moritz解析延拓解与Bjerhammar虚拟球面解的等价性[J]. 海洋测绘,2008,28(3):6-9) |
| [10] | Moritz H. Physical Geodesy[M]. New York:Springer,2006 |
| [11] | Moritz H. Advanced Physical Geodesy[M]. Beijing:Surveying and Mapping Press,1984(赫尔墨特·莫.高等物理大地测量学[M].北京:测绘出版社,1984) |
 2015, Vol. 40
2015, Vol. 40


