文章信息
- 王冰, 隋立芬, 王威, 马成
- WANG Bing, SUI Lifen, WANG Wei, MA Cheng
- GPS/陀螺组合测姿中整周模糊度的快速解算
- Rapid Resolution of Integer Ambiguity in Integrated GPS/Gyro Attitude Determination
- 武汉大学学报·信息科学版, 2015, 40(1): 128-133
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 128-133
- http://dx.doi.org/10.13203/j.whugis20130240
-
文章历史
- 收稿日期:2013-06-18
2. 信息工程大学地理空间信息学院, 河南 郑州, 450052;
3. 61741部队, 北京, 100094;
4. 61206部队, 北京, 100042
2. Institute of Surveying and Mapping, Information Engineering University, Zhengzhou 450052, China;
3. Unit 61741, Beijing 100094, China;
4. Unit 61206, Beijing 100042, China
利用GPS进行姿态测量,可以建立单基线观测模型解算天线间的相对位置,进而得到载体的姿态[1],也可以建立多基线观测模型直接解算载体的姿态[2]。这两种方法均为确定性算法。GPS载波相位的测量精度较伪距的测量精度至少高2~3个数量级,而利用载波相位观测值实现高精度的姿态测量必须快速和准确地确定整周模糊度。对于GPS载体姿态测量而言,基线长度及基线相对位置可以事先通过精确测量得到。因此,直接采用GPS导航定位中的模糊度解算方法无法充分利用先验信息,得到的整周模糊度解也并非最优解。为此,不少学者开展了相应的研究工作,提出了一系列算法[3, 4, 5, 6],利用基线长度信息缩小模糊度搜索空间,或者将其作为判断模糊度是否固定的依据,在一定程度上提高了模糊度解算的成功率及效率。这些算法共同的缺点是只利用了基线的长度约束信息。文献[7]对Lambda算法进行扩展提出了多变量约束Lambda方法(multivariate constrained Lambda,MC-Lambda),此方法直接建立关于方向余弦矩阵的多基线观测模型,将方向余弦矩阵的正交约束引入模糊度搜索过程,在很大程度上提高了模糊度的固定成功率。但该算法利用GPS当前历元伪距和载波相位观测值估计方向余弦矩阵和整周模糊度,由此得到的浮点解精度较低,而约束信息的引入使得模糊度的搜索空间不再为椭球体,增加了整周模糊度的搜索负担。
文献[8]指出,在典型的星敏感器/陀螺配置下,系统模型线性化误差对姿态确定精度的影响并不显著。但对于GPS观测值的精度而言,常用的改进的扩展Kalman滤波(MEKF)算法的截断误差可能导致滤波精度降低或者发散。因此,本文选择方向余弦矩阵表示姿态,建立GPS/陀螺姿态估计状态方程及观测方程,推导确定状态噪声模型。由滤波得到的是不考虑方向余弦正交约束、模糊度整数约束的浮点解,本文使用MC-Lambda方法对整周模糊度及方向余弦矩阵进行固定,然后回代解算常值漂移的固定解。
1 基于方向余弦矩阵的Kalman滤波算法 1.1 状态方程
定义载体坐标系相对参考坐标系的方向余弦矩阵为 R ,微分方程为[9]:
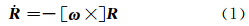
式中,ω为载体坐标系相对参考坐标系的角速度;[ω×]为斜对称矩阵。
采用陀螺测量角速度,测量模型表示为:
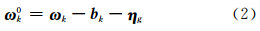
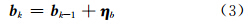
式中, ω k、 b k、 ω 0k分别为k时刻陀螺测量输出值、陀螺常值漂移、载体姿态角速度真值; η g、 η b分别是均值为0、方差为 Σ η g和 Σ η b的高斯白噪声。
与状态方程(1)对应的离散状态方程为:

式中,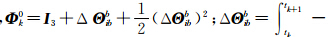

若历元间隔Δt很小,ω 0k变化足够小,则有Δ Θ bib=-[ω 0k×]Δt,将其代入 Φ 0k可得:

根据陀螺测量模型式(2),可得:
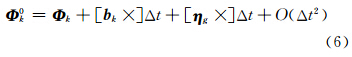
式中,
忽略式(6)的高阶项,将 Φ 0k代入式(4)得:


式中,ε k为状态方程噪声。
ε k为矩阵形式,建立其随机模型需要将其表示成向量的形式。定义vec ε k为 ε k的向量化形式,根据矩阵向量化定理[10],由式(8)可得:
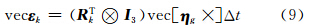
vec[η g×]可以表示为 η g的线性形式为:

式中,e j(j=1,2,3)为3×1维列向量,其第j个元素为1,其余元素为0。
将式(10)代入式(9)得:

定义 ε k的方差阵为 Q εk,根据方差协方差的传播定律由式(11)可得:
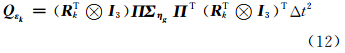
假定整周模糊度无跳变,建立整周模糊度的状态方程[11]:
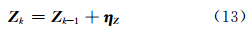
式中,η Z 是均值为0、方差为 ΣηZ 的高斯白噪声。
1.2 GPS观测方程
为了消除载波相位中电离层误差、对流层误差、卫星钟差、接收机钟差等大部分误差,本文选取双差载波相位观测值。若载体上安装 m+1个天线,其共视卫星数为n+1,选择某一天线作为主天线,仰角最高的卫星作为参考星,m条基线的双差载波相位观测量表示为[7]:
其中,Y 为n×m维双差载波相位观测量; Z 为n×m维双差整周模糊度; R 为方向余弦矩阵,满足 R T R = I ; B B 表示基线在载体坐标系中的坐标,为3×m维矩阵;模糊度系数阵为 A =λ I n;视向量阵为 S =[s1r1 … s1rn]T。 I n为n维单位向量,s jri为基线i关于卫星j、r的视向量差,r为参考星。
根据文献[7],多基线载波相位观测量的方差协方差阵表示为:
式中,Q y为单基线双差载波相位观测量的方差-协方差阵;
1.3 Kalman滤波器设计
式(3)、(7)、(13)为系统状态方程,式(14)为系统观测方程。可以看出,未知参数中方向余弦矩阵、整周模糊度均为矩阵形式,而经典Kalman滤波算法无法用于状态参数为矩阵的情况。因此,本文需要将系统状态方程式(7)和式(13)、观测方程式(14)进行向量化:
式中,R k,i(i=1,…,3)为方向余弦矩阵的第i列; I 3为3维单位矩阵。
选取向量化后的方向余弦矩阵、整周模糊度和常值漂移作为滤波器的状态值,即vec X k+1=[(vec R k+1)T (vec Z k+1)T ( b k+1)T]T,联合式(16)~(18)得到GPS/陀螺组合姿态确定系统模型:
式中,
基于方向余弦矩阵建立的GPS/陀螺组合姿态确定系统模型为线性模型,可采用经典滤波算法进行解算。利用滤波估计得到方向余弦矩阵、整周模糊度及常值漂移的浮点解,分别表示为
考虑模糊度的整数约束和方向余弦矩阵的正交约束,对滤波得到的浮点解进行固定即为解算下面最优化问题[7]:
对于任意的 Z很难存在一个R同时满足R =
根据式(21)定义整周模糊度搜索空间:
由于整周模糊度的搜索空间Ω(χ2) 不再为球搜索空间,不能使用Lambda方法进行搜索。针对非模糊度参数含有约束信息的整周模糊度解算问题,Teunissen对整数最小二乘估计理论进行扩展,给出了约束最小二乘估计的概念,提出了MC-Lambda用于多基线GPS整周模糊度的解算。
首先定义搜索空间目标函数F( Z )的上下界约束函数,表示为:
相应的整周模糊度搜索空间为:
根据上述定义给出整周模糊度搜索步骤:
1) 首先设定χ20值保证Ω2(χ2)非空。对Ω2(χ2)进行搜索得到使得F2( Z )最小的整周模糊度向量
2) 令 x2=F2(
3) 计算所有整周模糊度向量( Z ,R )对应的F( Z ),使得F( Z )最小的 Z及R ( Z )即为整周模糊度和方向余弦矩阵的固定解。
3 计算与分析
为了分析GPS测量噪声、陀螺测量噪声对算法性能的影响,仿真4种不同噪声条件的数据(见表 1),其中,Ω0(rad/s)表示初始姿态角速度,σg(°/h)表示陀螺测量噪声标准差,σb(°/h)表示常值漂移噪声标准差,σΦ(m)表示载波相位观测噪声标准差,σP(m)表示伪距观测噪声标准差。
陀螺角速度为 w =[cos(10Ω0t) cos(8Ω0t) cos(5.7Ω0t)],常值漂移[1 1 1]T °/h。GPS基线在载体坐标系中的坐标为
采用以下4种方案对整周模糊度进行解算。
1) 方案1(a)。基于GPS单历元载波相位、伪距观测值,采用Lambda方法解算整周模糊度,然后解算载体姿态。
2) 方案1(b)。在方案1(a)的基础上,整周模糊度解算采用了MC-Lambda方法。
3) 方案2(a)。利用5个历元的GPS载波相位、伪距观测值解算姿态矩阵及整周模糊度,将解算结果作为滤波初值。选定模糊度状态方程噪声阵 ΣηZ =0.000 1 I ,采用矩阵Kalman滤波求解整周模糊度、姿态矩阵及常值漂移的浮点解,使用Lambda方法解算整周模糊度,并返回固定姿态矩阵及常值漂移。
4) 方案2(b)。在方案2(a)的基础上,整周模糊度解算采用了MC-Lambda方法。
其中,方案1为单历元单频单独GPS观测值确定姿态,方案2为陀螺辅助单频单历元GPS姿态确定。方案1(a)、方案2(a)中整周模糊度解算不考虑方向余弦矩阵的正交约束,方案1(b)、方案2(b)中整周模糊度解算考虑方向余弦矩阵的正交约束。定义整周模糊度的固定成功率为模糊度固定成功历元数与总历元数的比值。4种方案的模糊度固定成功率如表 2、3所示,单历元整周模糊度解算耗时见表 4。
分析表 2,在单频单历元的情况下,MC-Lambda方法的整周模糊度固定成功率较Lambda方法得到了很大提高。在GPS载波相位/伪距观测噪声为0.01 m/0.25 m时,若卫星数大于5,此时MC-Lambda方法的整周模糊度固定成功率基本能够达到90%以上。但当GPS载波相位/伪距观测噪声为0.015 m/0.30 m时,MC-Lambda方法的整周模糊度固定成功率只能够达到70%以上。而我们都知道,模糊度固定错误将导致姿态定位精度有较大的偏差。分析MC-Lambda方法的整周模糊度搜索过程可以看出,增加约束使得搜索空间不再为椭球体,无法使用Lambda方法。分析表 3可以看出,虽然文献[13]给出了两种提高整周模糊度搜索效率的扩大与缩小策略,但由单频单历元得到的整周模糊度浮点解的精度较差,尤其观测条件较差的情况下(5颗星),这就导致MC-Lambda方法的搜索效率很低。
分析表 2、表 3可以看出,在GPS载波相位/伪距噪声为0.015 m/0.3 m、卫星数为5颗的情况下,两种滤波算法的整周模糊度固定成功率较低。本文对解算过程进行了分析,发现整周模糊度滤波初值较差,也即单历元的GPS观测值没有正确固定整周模糊度,偏离正确的整周模糊度较远。为此,本文对于整周模糊度的初值进行判断,即对整周模糊度正确与否进行判断,在认为整周模糊度未得到固定前,选择增加历元数k(k<10)直至整周模糊度固定,再开始滤波计算。对数据3、数据4的5颗星对应的数据重新解算,此时整周模糊度固定成功率为100%。分析表 3可以看出,整周模糊度浮点解精度提高后,利用MC-Lambda法进行整周模糊度固定的效率得到了很大的提高,在观测条件较差的情况下,效率提高了一个数量级左右。
4 结 语
在多台GPS接收机姿态确定中,基线长度及相对位置可以事先确定,MC-Lambda充分利用先验信息可以实现单频单历元的整周模糊度固定。但在GPS观测条件较差的情况下,尤其卫星数较少的情况下,利用单频单历元观测数据解算得到的整周模糊度浮点解精度较差,一方面加重了MC-Lambda方法的搜索负担,另一方面在多数情况下无法得到正确的整周模糊解。本文选择方向余弦矩阵表示姿态,建立GPS/陀螺姿态确定系统模型,利用滤波算法得到的不考虑方向余弦正交约束、模糊度整数约束的浮点解,然后使用 MC-Lambda方法固定整周模糊度及方向余弦矩阵。由于在整周模糊度浮点解的求解过程中采用了Kalman滤波算法,充分利用了多个历元的观测信息,改善了单个历元整周模糊度浮点解精度,在GPS 观测条件较差的情况下整周模糊度固定也能达到较高的成功率。需要指出的是,滤波方法中整周模糊度固定是否成功受初值的影响较大,这就需要我们对初值是否成功有较可靠的判断。


 ,主对角线上的元素为1,其余元素均为0.5。
,主对角线上的元素为1,其余元素均为0.5。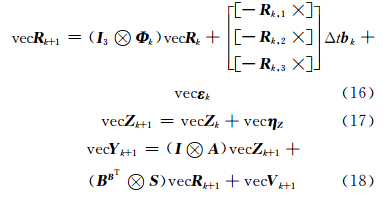
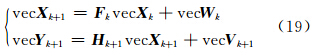
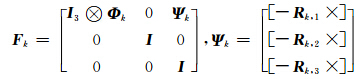



 ( Z )和 R T R = I ,而任意的( R ,Z )都存在 b =
( Z )和 R T R = I ,而任意的( R ,Z )都存在 b = 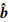 ( R ,Z ),因此,式(20)的目标函数等价于:
( R ,Z ),因此,式(20)的目标函数等价于:
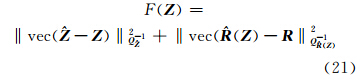


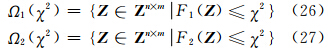
 ;
; ),枚举Ω1(span style="text-decoration:overline">x2)中的所有整周模糊度向量 Z ;
),枚举Ω1(span style="text-decoration:overline">x2)中的所有整周模糊度向量 Z ;
数据 Ω0 σg σb σΦ σP
1
0.001
0.500
0.300
0.010
0.250
2
0.001
5.000
3.000
0.010
0.250
3
0.001
0.500
0.300
0.015
0.300
4
0.001
5.000
3.000
0.015
0.300
 仿真历元间隔为0.5 s。首先,根据设定的初始姿态、陀螺角速度真值、陀螺噪声利用4阶龙格库塔法仿真得到载体在每个历元的姿态。然后,根据基线在载体坐标系中的坐标及当前历元载体的姿态,利用VISUAL软件[12]仿真2008-01-22中4个时段(4个时段的卫星数分别为5、6、7、8)的GPS载波相位及伪距观测值,每个时段选取2 000个历元。为了便于分析,对4个时段的卫星星座PDOP值进行计算,结果如图 1所示。可见,并非卫星数越多,观测条件越好。
仿真历元间隔为0.5 s。首先,根据设定的初始姿态、陀螺角速度真值、陀螺噪声利用4阶龙格库塔法仿真得到载体在每个历元的姿态。然后,根据基线在载体坐标系中的坐标及当前历元载体的姿态,利用VISUAL软件[12]仿真2008-01-22中4个时段(4个时段的卫星数分别为5、6、7、8)的GPS载波相位及伪距观测值,每个时段选取2 000个历元。为了便于分析,对4个时段的卫星星座PDOP值进行计算,结果如图 1所示。可见,并非卫星数越多,观测条件越好。

图 1 视卫星PDOP值
Fig. 1 Success Rate of Ambiguity Resolution
Using Initial Values of Different Accuracies
方案数据
方案1(a) 方案1(b)
数据1 数据2 数据3 数据4 数据1 数据2 数据3 数据4
5颗 0.00 0.00 0.00 0.00 69.6 69.5 41.2 41.3
6颗 0.10 0.10 0.00 0.00 90.7 90.0 75.4 75.4
7颗 1.70 1.45 0.00 0.05 97.1 96.9 83.8 84.1
8颗 12.1 10.4 0.40 0.70 95.0 95.2 86.3 88.6
方案数据
方案1(a) 方案1(b)
数据1 数据2 数据3 数据4 数据1 数据2 数据3 数据4
5颗 100.0 100.0 65.4 45.6 100.0 100.0 77.9 64.5
6颗 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0
7颗 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0
8颗 100.0 100.0 100.0 100.0 100.0 100.0 100.0 99.7
方案数据
方案1(a) 方案1(b)
数据1 数据2 数据3 数据4 数据1 数据2 数据3 数据4
5颗 580 579 980 982 27.0 27.0 27.4 25.7
6颗 328 328 875 866 39.7 39.4 37.1 37.4
7颗 96.3 96.7 100.7 100.5 51.9 51.5 47.0 47.1
8颗 104.2 104.1 115.3 117.8 62.4 61.3 58.8 62.5
| [1] | Liu Genyou, Ou Jikun. Determining Attitude with Single Epoch GPS Algorithm and Its Precision Analysis[J].Geomatics and Information Science of Wuhan University, 2003,28(6):732-735(刘根友,欧吉坤. GPS单历元定向和测姿算法及其精度分析[J]. 武汉大学学报﹒信息科学版,2003,28(6):732-735) |
| [2] | Axelrad P, Ward L M. Spacecraft Attitude Estimation Using the Global Positioning System: Methodology and Results for RADCAL[J]. Journal of Guidance, Control and Dynamics, 1996,19: 1 201-1 209 |
| [3] | Park C, Kim I, Lee J G, et al. Efficient Ambiguity Resolution Using Constraint Equation[C]. Position Location and Navigation Symposium, Atlanta, 1996 |
| [4] | Wang B, Miao L, Wang S, et al. A Constrained Lambda Method for GPS Attitude Determination[J]. GPS Solutions, 2009, 13:97-107 |
| [5] | Kuylen L V, Nemry P, Boon F, et al.Comparison of Attitude Performance for Multi-antenna Receivers[J]. European Journal of Navigation , 2006,4(2):1-9 |
| [6] | Park C, Teunissen P J G. A Baseline Constrained Lambda Method for Integer Ambiguity Resolution of GNSS Attitude Determination Systems[J]. Journal of Control, Robotics and Systems (in Korean), 2008, 14(6): 587-594 |
| [7] | Teunissen P J G. A General Multivariate Formulation of the Multi-Antenna GNSS Attitude Determination Problem[J]. Artificial Satellites, 2007,42(2):97-111 |
| [8] | Kuang Zhengde. Research on Non-linear Filter Methods for High Precision Satellite Attitude Determination[D]. Changsha: National University of Defense Technology,2009(匡正德.卫星高精度姿态确定中非线性滤波算法的研究[D].长沙:国防科技大学, 2009) |
| [9] | Zhang Renwei. Attitude Dynamics and Control for Satellite[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1998(章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998) |
| [10] | Zhang Xianda. Matrix Analysis and Applications[M]. Beijing: Tsinghua University Press,2004(张贤达. 矩阵分析与应用[M]. 北京:清华大学出版社,2004) |
| [11] | Scaccia M. Numerical Algorithms for Attitude Determination Using GPS[M]. Quebec, Canada :McGill University, 2011 |
| [12] | Verhagen S. Visualization of GNSS-related Design Parameters: Manual for the Matlab User Interface[R]. Delft Institute of Earth Observation and Space systems,Delft University of Technology,Delft,2006 |
| [13] | Giorgi G, Teunissen P J G, Buist P J. A Search and Shrink Approach for the Baseline Constrained Lambda: Experimental Results[C]. The International Symposium on GPS/GNSS, Tokyo, 2008 |
 2015, Vol. 40
2015, Vol. 40


