文章信息
- 姚宜斌, 刘劲宏, 张豹, 何畅勇
- YAO Yibin, LIU Jinhong, ZHANG Bao, HE Changyong
- 地表温度与加权平均温度的非线性关系
- Nonlinear Relationships Between the Surface Temperature and the Weighted Mean Temperature
- 武汉大学学报·信息科学版, 2015, 40(1): 112-116
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 112-116
- http://dx.doi.org/10.13203/j.whugis20130030
-
文章历史
- 收稿日期:2013-04-11
水汽在大气中所占的比例仅有0.1%~3%,却是大气中最活跃的成分[1]。水汽的相位变化所带来的巨大潜热,影响着大气垂直稳定度,对大气风暴系统的结构和演化起着十分重要的作用。水汽的平流和大气的环流所带来的潜热是地球南北半球能量平衡的重要因素[2, 3]。在干旱、洪涝、泥石流等地质灾害中,水汽也扮演着重要的角色。因此,大气水汽是监测及预报全球气候变化(包括暴雨在内的高影响天气或强对流天气)的一个非常重要的气象因子。全球平均温度和水汽含量也是反映全球气候变化的两个重要指标[4]。
文献[3]介绍了利用GPS技术探测水汽的基本原理,并推导出了可降水量(PWV)与天顶湿延迟(ZWD)之间的关系,使GPS技术正式成为水汽探测的一种重要手段。PWV与ZWD之间的关系可以表示为:

式中,Π为转换系数。根据文献[1]的定义,转换系数Π可表示为:

式中,ρw为液态水的密度;Rv为水汽气体常数;k′ 2、k3为大气折射常数[1]。由式(2)可知,Tm是求解转换系数Π的关键变量,由于ρw、Rv、k′ 2、k3均为已知常数,故转换系数Π的主要误差来自于Tm。
文献[5]已说明PWV的误差来源于计算误差、转换因子误差、模型误差。本文主要针对转换因子Π中的关键变量 Tm展开研究。
Tm与测站上空的温度、气压和水汽压有关,可通过式(3)近似计算:
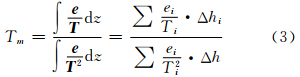
在没有温度和水汽垂直廓线的情况下无法根据式(3)计算Tm。利用Bevis Tm-Ts关系进行计算是最常用的方法[6]。该模型最初是由文献[3]利用美国中纬度地区的8 718次探空记录计算得出加权平均温度Tm和地表温度Ts之间存在线性函数关系。此后,文献[7]对全球分布的53个无线电探空站23 a探空资料的研究表明,Tm和Ts的相关性是随着测站地理位置与季节的变化而变化的。文献[2]建立了适合我国东部地区使用的逐月的Tm-Ts关系。文献[8]建立了适合武汉地区使用的Tm-Ts关系。文献[9]通过比较分析发现Tm-Ts单因素回归结果和 Tm-Ts、es、Ps (es为水汽压,Ps为气压)多因素回归结果没有显著差异,但基于本地探空数据的回归公式精度优于Bevis Tm-Ts关系模型。该线性模型广泛应用于区域Tm和Ts的拟合,但其完全是从统计学上得到的近似拟合公式,并没有数学上的推导,理论依据相对匮乏。
本文从Tm定义出发,在温度随高度线性递减的假定下,利用数学上内积的定义和柯西中值定理推导出了Tm与Ts之间的非线性函数关系,改变了以往纯统计学意义上的Tm随Ts线性变化的关系。
1 Tm与TS函数关系模型推导 1.1 内积和柯西中值定理1) 函数内积[10]。若 x (t)和 y (t)分别是变量t的函数向量,则它们的内积可以定义为:
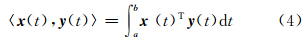
式中,变量t在 a,b 取值,且a
两个函数向量的夹角定义为: 式中,‖x(t)‖是函数向量 x (t)的范数,其定义为: 2) 柯西中值定理。如果有函数f(x)及F(x),那么在(a,b)内至少有一点ξ,使等式 成立。具体定义见文献[11],此处不再详述。 由于水汽基本集中在对流层,特别是低对流层,因此,几乎所有的湿延迟都发生在对流层,且其中大部分产生于低对流层,所以Tm将依赖于对流层温度廓线和水汽的垂直分布[2]。因此,在地基GPS气象学中,式(3)的积分区间为地面测站到对流层顶。这个区间很难精确确定,因此,本文采用气象学定义下的对流层顶代替进行计算。
设地面点高度为hs,对流层顶高度为h′,则积分区间为[hs,h′]。式(3)可记为: 由式(3)、(7)、(8)可知,水汽压 e 和温度 T 在测站上空是随高度h变化的连续函数,且Tm在区间内可导。设∫ 假定温度随高度呈线性递减,则任意高度的温度可由式(10)表达: 式中,hs为地表测站温度;δ为温度递减率;h为任意高度。
根据式(4)、(5)有: 记φ= 式(13)是根据加权平均温度与内积定义推导出来的,由于温度随高度的变化不能精确表达,因此式(13)无法精确求得。但在温度线性递减的假定下,‖ T ‖可由式(6)积分得出。因此,要推得因变量Tm与单一自变量Ts的关系,必须先求得φ与Ts的关系。
根据式(3)可知,水汽压和温度是随高度变化的函数,又由式(6)、(7)可知,存在唯一h2、h3使得式(11)、(12)表达为: 式中,e2、e3、T2、T3分别为高度h2、h3处的气压、温度值。
顾及φ= 由式(6),(10),积分式(16)中的‖ T ‖,得: 将式(17)整理可得: 由式(18)知,φ与 式中,a、b为待拟合系数。
为验证式(19)的合理性,亚洲平均海拔高为950 m,为方便计算取1 km,温度递减率取-6.5 K/km,对流层顶高度取11 km[2]。根据式(13),用我国2010年探空数据作φ图,白色曲线是根据式(19)进行拟合的曲线(见图 1)。其拟合均方根误差为6.95×10-5,这说明式(19)是合理的。
将式(19)代入式(13),顾及式(6)、(10),得: 将式(20)整理得: 为了更好地拟合式(21)中的系数,式(21)可简化表达为: 式中系数均为待拟合系数。
至此,本文建立了Tm与Ts推导与数理统计相结合的非线性函数关系表达式。由式(22)可知,Tm与Ts的关系并非是传统的由统计得出的线性关系。同时,由式(20)可知,在该函数模型下,Ts不变,Tm由地面站点位置与对流层顶的高度决定,且Tm与站点高度和对流层顶的平方和近似呈二次函数关系。因此,式(22)所表述的函数模型相对于线性函数模型,能较好地说明Tm与站点位置和对流层之间的关系。
本文采用R统计软件[12]对2010年我国78个探空站数据分别按线性模型和非线性模型对各自系数项进行拟合,结果见图 2。 图 2分别展现了线性拟合与非线性拟合的统计特性。从图 2中可以看出,非线性拟合曲线呈“S”形,在低温处与高温处明显弯曲,且在高温处的拟合明显好于线性拟合。从残差统计分布可以得出,非线性拟合相对于线性拟合具有更好的离散性。线性拟合标准差为4.192 K,非线性拟合标准差为4.116 K,相差0.076 K,这说明非线性稍好于线性拟合。
同时,为进一步探讨线性拟合与非线性拟合的差异,本文利用经度114°下我国7个探空站2010年的数据对线性和非线性函数进行拟合(见图 3)。 结合图 2,从图 3中可以看出,拟合曲线在两端处的拟合结果优于线性拟合,而在曲线中间两者拟合相差不大。由于极地和赤道附近气温是最低和最高的,一般处于Tm与Ts关系的两端,因此,可认为利用全球探空站数据拟合平均温度与地表温度的关系,非线性拟合在这两端将显著优于线性拟合。图 3中的线性拟合标准差为3.923 K,非线性拟合标准差为3.786 K,两者相差0.14 K,相对于0.076 K,非线性拟合精度明显提高。这证明了非线性好于线性拟合,能较好地反映Tm与Ts的关系。
除了Ts测定误差,本文公式是基于温度随高度线性递减的假定推得的。这一假定是把式(10)中的δ视为常数进行拟合的。δ不宜作为一个常量对待,需要建立随高度变化的δ模型来削弱因假定引起的误差。
探空站分布不均匀,以及气候差异使得Ts不能完全反映全国的变化,这使得拟合曲线在低温地区拟合较差。
本文认为文献[14]提到的加权平均温度的精度与地理位置的关系主要是通过各地海拔高度的不同体现的这一结论有待商榷。一般地,赤道附近及热带对流层顶高度约15~20 km,极地和中纬度带高约8~14 km[1]。因此,相对于测站海拔高度,区域内的相对高度h0受到对流层以及对流层顶分界的影响更大,这无疑会影响到非线性函数模型的系数拟合精度。
4 结 语
本文基于垂直温度随高度线性递减的假设,从理论与数理统计上推导了 Tm与Ts之间的非线性函数关系,改变了过去加权平均温度Tm与测站温度Ts之间的线性关系式。本文用中国区域探空站数据拟合线性模型和非线性函数模型,结果表明,非线性函数模型拥有较小均方根误差,其拟合曲线与实测Tm随Ts 的变化趋势更加吻合。


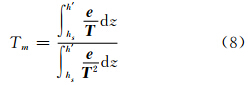
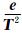 dz与∫
dz与∫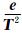 dz的原函数分别为f、F。因此,在对流层中必定存在唯一高度h1使得式(9)成立:
dz的原函数分别为f、F。因此,在对流层中必定存在唯一高度h1使得式(9)成立: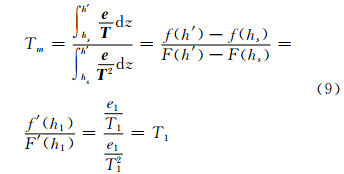
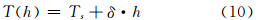
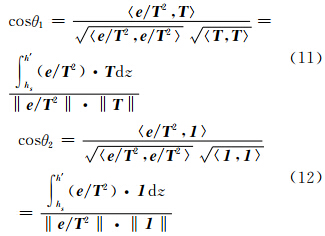
 ,h0=h′-hs,φ与温度 T 和水汽压 e 相关,顾及式(8),得/p>
,h0=h′-hs,φ与温度 T 和水汽压 e 相关,顾及式(8),得/p>
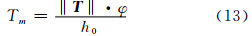

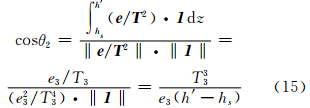
 ,代入式(14)、(15)得:
,代入式(14)、(15)得: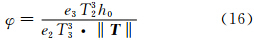
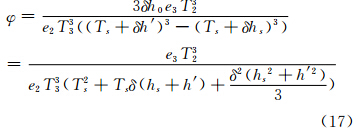

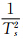 成正比。T2与T3之比近似为1,且Ts的倒数又非常小,式(18)近似表达为:
成正比。T2与T3之比近似为1,且Ts的倒数又非常小,式(18)近似表达为:

图 1 我国78个探空站数据对φ进行地表温度的二次线性拟合
Fig. 1 Second-Order Function of φ Fitting Based on Data of 78 Radiosonde Stations in China Area



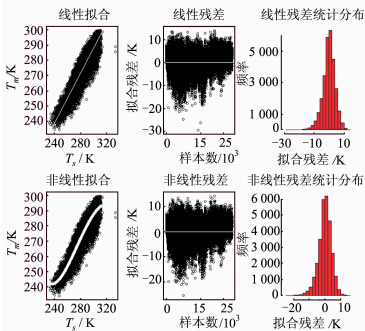
图 2 线性与非线性拟合的统计性质
Fig. 2 Statistical Properties of Linear and Nonlinear Fitting
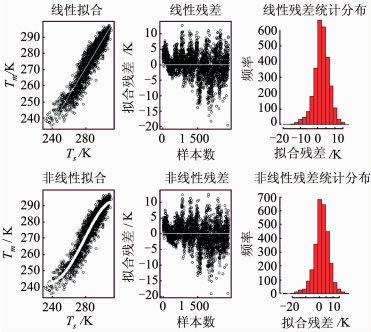
图 3 同经度下线性与非线性拟合
Fig. 3 Linear and Nonlinear Fitting at the Same Longitude
| [1] | Sheng Peixuan,Mao Jietai,Li Jianguo,et al. Atmosphere Physics[M].Beijing:Peking University Press,2011(盛裴轩,毛节泰,李建国,等.大气物理学[M].北京:北京大学出版社,2011) |
| [2] | Li Jianguo,Mao Jietai,Li Chengcai.The Principle of Remote Sensing Water Vapor Distribution Using Global Positioning System and the Regression Analysis of the Weighted Average Temperature in China Eastern Region[J]. Acta Meteorologica Sinica,1999,57(3):283-291(李建国,毛节泰,李成才.使用全球定位系统遥感水汽分布原理和中国东部地区加权“平均温度”的回归分析[J].气象学报,1999,57(3):283-291) |
| [3] | Bevis M,Businger S,Herring T A,et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. J Geophys Res, 1992,97(D14):15 787-15 801 |
| [4] | Chen Xiaojuan,Hu Chengsheng,Wang Zhanwei. Research and Application Progress of National and International GPS Meteorology[J]. Science of Surveing and Mapping,2010,35(3):216-218(陈笑娟,扈成省,王占伟.国内外GPS气象学的若干研究应用进展[J].测绘科学,2010,35(3):216-218) |
| [5] | Chen Junyong. On the Error Analysis for the Remote Sensing of Atmospheric Water Vapor by Ground Based GPS[J]. Acta Geodaetica et Cartographica Sinica, 1998,27(2):113-118(陈俊勇.地基GPS遥感大气水汽含量的误差分析[J].测绘学报,1998,27(2):113-118) |
| [6] | Li Guoping. Huang Dingfa Ground-Based GPS Meteorology[M].Beijing:Science Press,2010(李国平,黄丁发.地基GPS气象学[M].北京,科学出版社,2010) |
| [7] | Ross R J, Rosenfeld S.Estimating Mean Weighted Temperature of the Atmosphere for Global Positioning System Applications[J]. J Geophys Res,1997,102(D18):21 719-21 730 |
| [8] | Wang Yong,Liu Lintao,Hao Xiaoguang.The Application Study of the GPS Meteorology Network in Wuhan Region[J]. Acta Geodaetica et Cartographica Sinica,2007,36(2):142-145(王勇,柳林涛,郝晓光.武汉地区GPS气象网应用研究[J],测绘学报,2007,36(2):142-145) |
| [9] | Wang Xiaoying,Song Lianchun,Dai Zaiqiang,et al.Feature Analysis of Weighted Mean Temperature Tm in Hong Kong[J]. Journal of Nanjing Uinversity of Information Science and Technology:Nature Science Editon, 2011,3(1):47-52 (王晓英,宋连春,戴仔强,等.香港地区加权平均温度Tm特征分析[J].南京信息工程大学学报(自然科学版),2011,3(1):47-52) |
| [10] | Zhang Xianda.Matrix Analysis and Application[M].Beijing:Tsinghua University Press, 2004(张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004) |
| [11] | Tongji University Department of Mathematics. Higher mathematics[M].Beijing:Higher Education Press, 2008(同济大学数学系.高等数学[M].北京:高等教育出版社,2008) |
| [12] | Cryer J D,Chan K S .Time Series Analysis with Applications in R[M].Translated by PAN Hongyu,et al. Beijing:China Machine Press.(Cryer D, Chan K S .时间序列分析及应用[M].潘红宇.北京:机械工业出版社,2011) |
| [13] | Yu Shengjie, Liu Lintao.Validation and Analysis of the Water-vapor-weighted Mean Temperature from Tm-Ts Relationship[J]. Geomatics and Information Science of Wuhan University, 2009,34(6): 741-744 (于胜杰,柳林涛 .水汽加权平均温度回归公式的验证与分析[J].武汉大学学报·信息科学版,2009, 34(6):741-744) |
| [14] | Wang Xiaoying,Dai Ziqiang,Cao Yunchang, et al. Weighted Mean Temperature Tm Statistical Analysis in Ground-based GPS in China[J].Geomatics and Information Science of Wuhan University, 2011,36(4):412-416(王晓英,戴仔强,曹云昌,等.中国地区地基GPS加权平均温度Tm统计分析[J].武汉大学学报·信息科学版,2011,36(4): 412-416) |
 2015, Vol. 40
2015, Vol. 40


