文章信息
- 陈西江, 花向红, 邹进贵, 贺小星
- CHEN Xijiang, HUA Xianghong, ZOU Jingui, HE Xiaoxing
- 光斑影响下激光点云的不确定性评价
- Uncertainty Evaluation of Laser Points Cloud Under the Influence of Spot
- 武汉大学学报·信息科学版, 2015, 40(1): 107-111
- Geomatics and Information Science of Wuhan University, 2015, 40(1): 107-111
- http://dx.doi.org/10.13203/j.whugis20130118
-
文章历史
- 收稿日期:2014-05-13
2. 武汉大学测绘学院, 湖北 武汉, 430079;
3. 武汉大学灾害监测与防治研究中心, 湖北 武汉, 430079
2. School of Geodesy & Geomatics, Wuhan University, Wuhan 430079, China;
3. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China
理论上,激光射线是沿着激光光束的中心方向的,但实际上由于震动或系统误差的影响,激光射线可能会偏离激光光束的中心方向,而激光束在物体上形成的光斑便是激光点位不确定性的范围,由文献[1]可知,激光的位置可能是光斑中的任意位置,体现了激光点位在光斑中的不确定性。由于信息论中的熵是信源平均不确定度的度量指标,可以将信息熵引入到点位不确定性的度量指标中。文献[2]利用误差熵对截断误差的不确定性进行研究。文献[3]以线元不确定性为实例建立了空间数据不确定性的混合熵模型,并给出了线元不确定性的熵带分布,验证了利用熵进行空间数据不确定性研究的可行性。文献[4]根据线元端点随机矢量的方差-协方差矩阵,将误差熵模型扩展到面元的误差熵环模型,该模型相对于面元误差环,无需事先设定置信水平,同时考虑了边界线上误差分布不均匀的特点。文献[5,6]分析了光斑大小对点云角度分辨率的影响,进而确定了光斑对点位不确定性的影响。由文献[7]分析可知,根据激光特性,激光点位近似服从高斯分布。利用3σ与光斑大小的关系确定点位协方差矩阵,由于光斑大小受入射角的影响,在推导入射角对点位协方差影响的基础上,分析了入射角对协方差矩阵的影响。本文根据激光点位概率密度函数,推导了激光点位的信息熵,并利用信息熵与误差熵的关系得到激光点位误差熵模型,通过分析激光点位误差熵公式中的变量可确定点位误差熵即是光斑面积的线性形式。因此,通过计算光斑面积即可确定点云误差熵,利用误差熵便可实现对点云不确定性的评价。 1 激光点位概率密度函数 1.1 光斑大小
光斑大小由激光波束宽度决定,是激光点位不确定性的范围。关于光斑大小的计算方法有很多种,文献[8,9]给出了两种光斑大小计算公式。文献[9]同时考虑了发射孔径 D0、距离S及S对应的光斑直径D的影响,对两种公式进行组合来计算光斑大小,其表达式为:
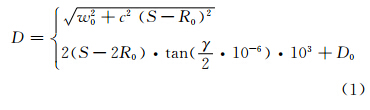
式中,R0为激光束的束腰半径;w0为R0处光斑直径;c为常数;γ为光束发散角。
式(1)同时顾及了发射孔径D0及S处光斑直径D的影响,能够较为准确地对光斑大小进行计算,本文将依据式(1)计算光斑大小。
入射角为0时,光斑大小可直接根据式(1)计算。文献[9]给出了光斑长轴长度随入射角变化的公式,如式(2)所示。而光斑短轴不随入射角的改变而改变。
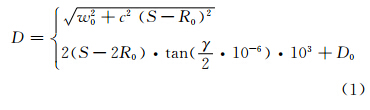
式中,β为激光波束宽度;S为扫描距离;a为入射角。 1.2 激光点位概率密度函数
脉冲中的能量近似服从对称的高斯分布(正态分布),从而有基于高斯分布的光斑中激光点位概率密度函数,如式(3)所示:

式中, 表示水平、垂直方向;δ表示光斑直径。
表示水平、垂直方向;δ表示光斑直径。
由于水平或垂直方向的点位落在(-3σ,3σ)区间内的概率达到了99.7%,所以可得到水平或垂直方向的点位中误差,如式(4)所示:

在考虑入射角a影响的情况下,有协方差矩阵如式(5)所示:

根据式(3)、(5)构建基于高斯分布的激光点位不确定性的概率密度函数模型。 2 基于误差熵的点云不确定性分析 2.1 光斑中点位不确定性误差熵模型
根据信息熵的定义可以得到激光点位在光斑中信息熵的统一表达式,如式(6)所示:
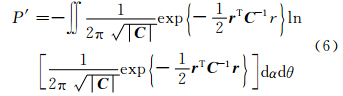
将式(6)化为标准误差椭圆的形式为:

式中,λ1,λ2为误差椭圆半轴长。
将椭圆形式化为标准误差圆形式:

利用极坐标进行积分可得:
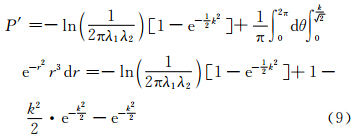
式中,k为误差椭圆缩放系数。
当k=3时,根据式(9),有:

式中,a为入射角;D为入射角为0时的光斑直径。
依据信息熵可以推导激光点位误差熵,如式(11)所示:

式(11)是激光点位误差熵的表达式。
根据式(11)的误差熵便可计算出每个激光点位在光斑中的不确定性大小,从而实现了对点位不确定性的量化。 2.2 点云误差熵模型
由式(11)可知,误差熵只与误差椭圆的长半轴λ1和短半轴λ2有关,而λ1、λ2是光斑长轴及短轴的1/6,则将式(11)演变为误差熵与光斑大小的关系式,如式(12)所示:

式中,a为光斑长半轴;b为光斑短半轴。
假设所有光斑的总面积为S总,总激光点位数为n个,则根据光斑总面积可得到点云总误差熵及平均每个激光点位的误差熵为:
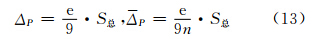
根据式(1)计算距离及入射角对点位不确定性的影响,结果如图 1所示。
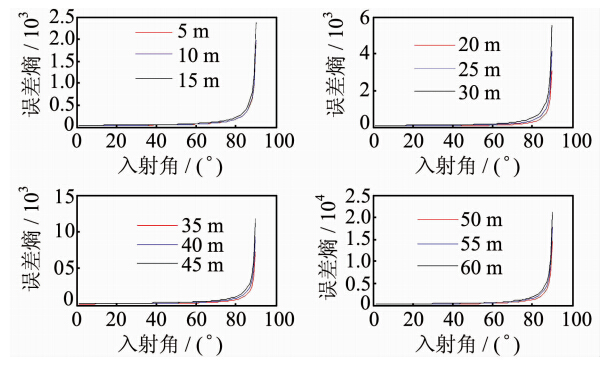
|
| 图 1 不同距离入射角对点位不确定性的影响 Fig. 1 Influence of Incident Angle on the Positional Uncertainty at Different Distances |
由图 1可知,随着入射角的增加,激光点位误差熵呈现增大的趋势,误差熵受入射角变化趋势影响较大,而受距离的影响较小,即入射角对激光点位不确定性的影响大于距离对激光点位不确定性的影响。根据不同距离处的误差熵可知,误差熵随着距离的增加呈现递增的趋势,距离越大激光点位不确定性越大。由入射角对激光点位误差熵的影响可知,在入射角小于9°时,可以不考虑其对点位不确定性的影响。3.2 实例分析
采用RIEGL VZ-400三维激光扫描仪正对着墙体进行扫描,扫描间隔分别设置为5 mm、8 mm。由式(1)、(2)计算每个点光斑大小,结果如图 2、3所示。
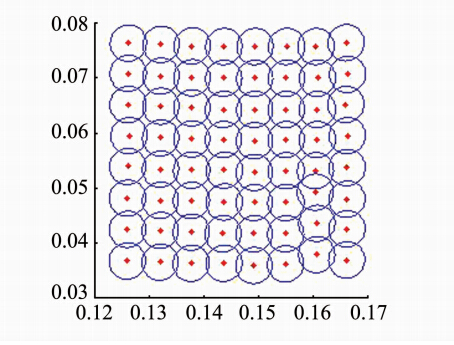
|
| 图 2 扫描间隔为5 mm的光斑 Fig. 2 Spot of Scan Interval 5 mm |
由图 3可知,相邻光斑无交集。对于图 2相邻光斑满足相交情况,在考虑入射角影响的情况下,利用式(10)、(11)计算不同扫描间隔下每个点对应的信息熵及误差熵,结果如表 1所示。
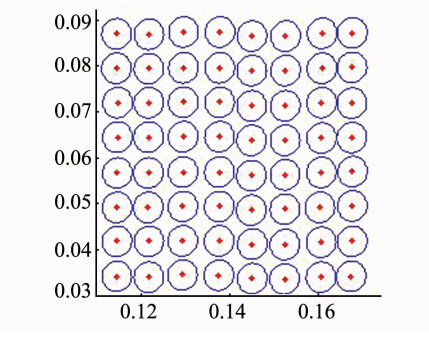
|
| 图 3 扫描间隔为8 mm的光斑 Fig. 3 Spot of Scan Interval 8 mm |
由表 1可知,扫描间隔为5 mm与扫描间隔为8 mm的信息熵相差最大都是0.000 18,误差熵相差最大的是0.003 1。因此,在相同距离扫描同一个目标时,扫描间隔对单个激光点位的信息熵和误差熵影响很小。根据每个光斑误差熵的计算结果,在不考虑光斑相交的情况下,利用式(13)计算总误差熵及平均每个激光点位的误差熵。在扫描间隔分别为5 mm、8 mm时,总误差熵分别为670.770 6、670.791 4,平均误差熵分别为10.480 8、10.481 1。这说明不同扫描间隔的总误差熵和平均误差熵几乎相同,即由光斑造成的激光点云不确定性相同。但由图 2可知,光斑与光斑之间存在交集,即存在重复面积,而由误差熵与光斑面积的关系式(12)可知,误差熵反应的正是光斑面积表达形式。所以,如果不考虑扫描间隔对光斑之间相交的影响,势必会造成误差熵的重合,使得计算得到的点云数据不确定、不真实。
| 1 | 2 | … | 64 | ||
| 扫描间隔5 mm | p′ | 3.043 | 3.043 | … | 3.043 |
| Δp′ | 10.482 | 10.481 | … | 10.48 | |
| 扫描间隔8 mm | p′ | 3.043 | 3.043 | … | 3.043 |
| Δp′ | 10.483 | 10.483 | … | 10.481 | |
为了真实反应点云数据的不确定性,利用误差熵与光斑面积的关系得到真实的误差熵。在扫描间隔分别为5 mm、8 mm时,总误差熵分别为356.850 6、670.791 4。平均误差熵分别为5.575 8、10.481 1。这说明在考虑了光斑相交的情况下,5 mm扫描间隔的误差熵要小于8 mm扫描间隔的误差熵。虽然每个激光点位的不确定性相同,但扫描间隔为5 mm的点云不确定性更小,整个点云的误差区间更小。 4 结 语
由于信息熵反应的是信息量的大小,本文将信息熵引入到光斑影响下点云不确定性的评价中,利用激光点位概率密度函数推导了激光点位在光斑中的信息熵,依据误差熵与光斑面积的关系得到了点云实际的误差熵,从而对点云实际的不确定性情况进行了评价。
1) 依据误差熵与光斑面积的关系,得到同一目标两次不同扫描间隔的点云误差熵,光斑相交的面积越大,其误差熵越小,单个激光点位的误差熵也就越小,所反应的点云不确定性也就越小。
2) 激光点位误差熵能够在一定程度上反映激光点位在光斑中的不确定性,整个点云的误差熵考虑了相邻激光光斑重合情况,是一种平均意义上的度量指标。采用误差熵可以描述点云实际的误差区间情况。
3) 由于入射角的影响,光斑投影到目标上的大小呈现不平衡的特点,激光点位在光斑中的分布也就呈现不平衡的特点。利用误差熵对点云的不确定性进行研究可以反映点云误差区间的实际情况,具有一定的价值。
| [1] | Lichti D D, Gordon S J. Error Propagation in Directly Georeferenced Terrestrial Laser Scanner Point Clouds for Cultural Heritage Recording[C]. FIG Working Week ,Athens, Greece,2004 |
| [2] | You Yangsheng, Ma Li , Liu Xing. On Estimation of Error Entropy[J]. Geomatics and Information Science of Wuhan University, 2008,33(7):748-751(游扬声,马力,刘星.误差熵的估计问题研究[J]. 武汉大学学报·信息科学版,2008,33(7):748-751) |
| [3] | Shi Yufeng, Shi Wenzhong, Jin Fengxiang. Hybrid Entropy Model of Spatial Data Uncertainty in GIS[J]. Geomatics and Information Science of Wuhan University, 2006,31(1):82-85(史玉峰,史文中,靳奉祥.GIS中空间数据不确定性的混合熵模型研究[J]. 武汉大学学报·信息科学版,2006, 31(1) : 82-85) |
| [4] | Li Dajun,Gong Jianya,Xie Gangsheng,et al. The Model of Error Entropy of Area Unit in GIS[J]. Acta Geodaetica et Cartographica Sinica,2003,32(1):31-35(李大军,龚健雅,谢刚生,等. GIS中面元的误差熵模型[J]. 测绘学报,2003,32(1):31-35) |
| [5] | Chen Xijiang, Hua Xianghong,Qiu Weining, et al. Accuracy Evaluation of point cloud angular resolution[J]. Geomatics and Information Science of Wuhan University, 2013,38(9):1 044-1 047(陈西江,花向红,邱卫宁,等. 点云角度分辨率精度评定[J]. 武汉大学学报·信息科学版,2013,38(9):1 044-1 047) |
| [6] | Yang Ronghua,Hua Xianghong,Qiu Weining, et al. Research on the Point Cloud Angular Resolution of Terrestrial laser Scanners[J]. Geomatics and Information Science of Wuhan University, 2012,37(7):851-853(杨荣华,花向红,邱卫宁,等. 地面三维激光扫描点云角度分辨率研究[J]. 武汉大学学报·信息科学版,2012,37(7):851-853) |
| [7] | Schaer P, Skaloud J, Landtwing S, et al. Accuracy Estimation for Laser Point Cloud Including Scanning Geometry[C]. Mobile Mapping Symposium, Padova,Italy, 2007 |
| [8] | Lichti D D. Angular Resolution of Terrestrial Laser Scanners [J].The photogrammetric record,2006, 21(14):141-160 |
| [9] | Yang Ronghua. Resarch on Point Cloud Angular Resolution and Processing Model of Terrestrial Laser Scanning[D]. Wuhan: Wuhan University, 2011(杨荣华.地面三维激光扫描点云角度分辨率与数据处理模型研究[D]. 武汉:武汉大学,2011) |
 2015, Vol. 40
2015, Vol. 40



